2. 西安建筑科技大学机电工程学院, 陕西 西安 710055
2. School of Mechanical and Electrical Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
自1990年Pecora和Carroll成功地实现混沌系统同步以来[1],由于混沌同步在保密通信、 控制领域等方面有着巨大的潜在应用前景,使其得到了广泛和深入的研究,各种同步现象不断被发现,包括完全同步[1]、 相同步[2]、 延迟同步[3, 4]、 广义同步[5]、 投影同步[6]等. 其中,延迟同步是一类重要的同步现象. 由于信号传输时间的影响和有限的开关速度,实际上完全的混沌同步是不可能的. 例如,在电话通信系统中,接听方在时间t时刻所听到的声音通常是发送方在t-τ时刻的声音[7]. 所以,在很多情况下,我们更有理由要求响应系统和驱动系统滞后固定时间τ同步,称为延迟同步.
分数阶微积分的提出已经有300多年的历史了,但只是在最近20几年它才成为科学研究的焦点. 人们在许多科学和工程领域都发现了分数阶动力学行为,包括黏弹性系统、 电介质极化、 电极—电解液极化、 电磁波、 生物工程等. 并且,在由分数阶微分方程描述的非线性系统中重新发现了混沌现象和超混沌现象. 比如分数阶Chen系统[8],分数阶洛伦兹系统[9],分数阶Duffing系统[10],分数阶Liu系统[11],分数阶Lü系统[12]和分数阶超混沌Chen系统[13],分数阶超混沌洛伦兹系统[14]等.
与整数阶混沌系统相比,分数阶混沌系统具有更为复杂的动力学行为,因而具有更强的保密性和抗破译能力. 近年来,许多学者开始研究分数阶混沌系统的同步问题. 自从Li等人首次研究了分数阶混沌系统的同步难题后[15],许多方法和技术已经被提出[16, 17, 18, 19, 20, 21, 22].
但是,这些混沌同步方法讨论的大都是确定的分数阶混沌系统,并未考虑建模误差、 测量误差、 结构变化、 环境噪声等因素. 在实际应用中,系统中通常存在的这些因素所造成的不确定和外部干扰都是不可避免的,这些因素对同步的质量、 性能有着有害的影响.
综上所述,研究不确定分数阶混沌系统的延迟同步有着重要的实际意义. 然而,对于不确定分数阶混沌系统的延迟同步的研究却鲜有报道. 本文利用滑模控制的抗干扰性,结合主动控制方法,提出了一个含有分数阶项的主动滑模控制器,实现了不确定分数阶混沌系统、 超混沌系统的延迟同步.
2 分数阶微积分 2.1 分数阶微积分的定义在分数阶微积分理论的发展过程中,出现了多种分数阶微分的定义[23],其中应用较多的有Riemann-Liouville(R-L)分数阶微分定义和Caputo分数阶微分定义. R-L定义常用在纯数学理论研究领域; 由于Caputo定义更容易处理分数阶微分方程的初值问题,因而常用在实际工程中.
R-L定义如下
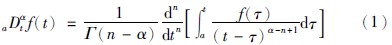
其中n是不小于α的第1个整数,即n-1<α 本文采用了Caputo定义,f(t)的分数阶微分定义如下 其中m是不小于α的第1个整数,即m-1<α 目前,由于分数阶微分方程没有精确的数值解析解,人们已经提出了多种近似求解方法,常用的方法主要有两种: 一个是频域—时域方法[24, 25],另一个就是基于Adams-Bashforth-Moulton算法的预估—校正方法[26, 27, 28]. 下面简要介绍本文采用的预估—校正方法,即广义的Adams-Bashforth-Moulton算法,考虑下面的分数阶微分方程 和它的初始条件 方程(4)和Volterra积分方程等价[29],积分方程描述如下 令h=T/N,tn=nh(n=0,1,…,N). 方程(5)可以离散化为 式中 数学分析表明式(5)与式(6)的近似误差为 其中p=min(2,1+α). 分数阶线性系统的稳定性已经得到了充分研究,文[30, 31]给出了判断分数阶系统稳定性的充要条件. 考虑下面的自治系统 其中,x∈Rn,A∈Rn×n,0<α<1为分数阶数. 如果矩阵A的特征值λ满足arg(λ)>απ/2,则分数阶系统(11)就是渐近稳定的. α阶线性系统的稳定区域如图 1所示. 考虑下面的α阶分数阶混沌系统作为驱动系统 其中x=(x1,x2,…,xn)T∈Rn是状态向量,F: Rn→Rn是连续的向量函数,A∈Rn×n,Ax和F(x)分别表示驱动系统的线性部分和非线性部分. 响应系统由下式给出, 其中y=(y1,y2,…,yn)T∈Rn是状态向量,G: Rn→Rn是连续的向量函数,B∈Rn×n,By和G(y)分别表示响应系统的线性部分和非线性部分,Δg(y): Rn→Rn是响应系统的未知部分,d(t): Rn→Rn是外部干扰,控制器u=(u1,u2,…,un)∈Rn加到响应系统,以实现驱动系统和响应系统的延迟同步. 定义同步误差为e=y(t)-x(t-τ)=y(t)-xτ,其中xτ=x(t-τ),τ代表延迟时间. 定义 对于驱动系统(12)和响应系统(13),如果存在一个有效的控制器u使得下面的等式成立,就称驱动系统和响应系统二者之间实现了延迟同步. 其中,‖·‖是向量的范数. 在t-τ时刻,方程(12)可以重写为 由同步误差的定义,式(13)和式(15)间的动态系统误差可以描述为 其中,M(xτ,y)=(B-A)xτ+G(y)-F(xτ). 根据主动控制设计策略[16],控制器可以设计为 把式(17)代入式(16)得到误差系统 基于滑模控制方法[17],H(t)可以设计如下: 其中K=[k1 k2 k3… kn]T为常数增益向量,w(t)∈R为控制输入,且满足下列条件 这里s=s(e)是满足要求的滑模面. 于是误差系统写为 在这里,滑模面设计为 其中C=[c1 c2 c3 … cn]是常数向量. 当系统处于滑模面上,被控系统须满足如下条件: 设计如下的分数阶滑模到达律 其中sgn(·)是符号函数,系数p>0,这样的选择满足滑模条件,并保证发生滑模运动. 联立式(21)和式(22),得到 由式(24)和式(25)求得控制输入为 由于Δg(y)和d(t)是未知的,所以真正的控制输入选择如下 最终可以得到控制器u 定理 从任意初始条件出发,如果响应系统由式(28)得到的控制器u控制,那么同步误差系统的轨迹将在有限时间内沿滑模面收敛到零. 也就是说,系统(12)和(13)间实现了延迟同步. 证明 考虑如下李亚普诺夫函数 对式(29)求导可得 这里假定D1-α(CΔg(y))和D1-α(Cd(t))是有界的且边界分别是a和b. 如果p≥a+b,则V·≤0. 可以看出,V是正定的,V·是负定的. 根据李亚普诺夫稳定理论,被控系统是稳定的,误差信号e(t)随时间到达无穷,渐近收敛到零. 这表明两个分数阶混沌系统实现了延迟同步,证毕. 为了说明上述方法的有效性,在这里给出两个数值仿真实例. 一个是分数阶Lü系统和分数阶Liu系统间的延迟同步,另一个是分数阶超混沌Lorenz系统和分数阶超混沌Chen系统间的延迟同步. 数值仿真是利用Matlab 7.0软件实现的,微分方程采用4阶Runge-Kutta算法,时间步长设定为0.001 s. 分数阶Lü系统描述如下 其中,x1、 x2、 x3是状态变量,a、 b、 c是系统参数. 当a=36、 b=3、 c=20、 α=0.93时,分数阶Lü系统处于混沌状态,其混沌吸引子如图 2所示. 分数阶Liu系统描述如下 其中,y1、 y2、 y3是状态变量,θ、 β、 δ、 γ、 λ是系统参数. 当θ=10、 β=40、 δ=2.5、 γ=1、 λ=4、 α=0.93时,分数阶Liu系统处于混沌状态. 其混沌吸引子如图 3所示. 令系统(31)为驱动系统,则响应系统描述如下: 系统(31)和系统(33)的初值分别取为(0.8,0.5,0.1)和(0.8,0.6,0.4),分数阶数α=0.93,延迟时间τ=0.1 s,不确定和外部干扰分别为Δg(y)=[0.2siny1,0.2siny2,0.2siny3],d(t)=[-0.1sin(10t),-0.1sin(20t),0.2sin(20t)],u=[u1,u2,u3]T是控制输入. 根据上面滑模控制器的设计步骤,选择控制器参数C=[1 1 -1],K=[1 1 1]T,p=2. 当t=5 s时,加入控制作用,相应的延迟同步误差和状态响应如图 4和图 5所示. 从图 4和图 5中可以看出,在延迟同步控制器的作用下延迟同步误差e1,e2和e3平滑、 渐近地收敛到零; 响应系统中的状态变量逐渐跟踪了驱动系统中相对应的状态变量的混沌轨迹,两者形状完全一致,仅在时间上有一个τ的延迟. 明显的,在具有不确定和外部干扰的情况下,分数阶Lü系统和分数阶Liu系统之间仍实现了延迟同步. 分数阶超混沌洛伦兹系统描述如下: 其中x1、 x2、 x3、 x4是状态变量,λ、 β、 θ、 γ是系统参数. 当λ=10、 β=28、 θ=8/3、 γ=-1、 α=0.98时,此系统是超混沌的,其混沌吸引子见图 6. 分数阶超混沌Chen系统描述如下: 其中,y1、 y2、 y3、 y4是状态变量,a、 b、 c、 d,r是系统参数,当a=35、 b=7、 c=12、 d=3、 r=0.5、 α=0.98时,系统是超混沌的,其吸引子见图 7. 令系统(34)为驱动系统,则响应系统为 在数值仿真中,驱动系统和响应系统的初值分别取(0.1,1,-0.5,1)和(0.1,0,-0.1,0.1),分数阶数α=0.98,延迟时间τ=0.1 s,不确定性为Δg(y)=[0.2siny1,0.2siny2,0.2siny3,0.2siny4],外部干扰为d(t)=[-0.1sin(10t),-0.1sin(20t),0.2sin(20t),0.2sin(20t)],u=[u1,u2,u3,u4]T是控制输入. 根据上面滑模控器的设计步骤,选择控制器参数C=[1 1 1 -1],K=[1 1 1 1]T,p=0.5. 当t=5 s时,加入控制作用,相应的延迟同步误差和状态响应如图 8和图 9所示. 从图 8中看出,在加入控制作用后,延迟同步误差e1,e2和e3经过短暂的过渡后平稳地趋于零. 从图 9中可以看出,响应系统(36)的状态曲线都跟踪上驱动系统(34)的状态曲线,只是滞后0.1 s的时间,即,x1(t-0.1)=y1(t),x2(t-0.1)=y2(t),x3(t-0.1)=y3(t),x4(t-0.1)=y4(t). 可见,在含有不确定性和外部干扰的情况下,分数阶超混沌洛伦兹系统和分数阶超混沌Chen系统之间实现了延迟同步. 本文研究了含有不确定性和外部干扰情况下的分数阶混沌(超混沌)系统的延迟同步,利用主动控制和滑模控制二者的优点,设计出一种含有分数阶项的延迟同步控制器. 该控制器设计简单,适应范围广. 两个实例的数值仿真证明了此方法具有较强的鲁棒性和抗干扰能力. 

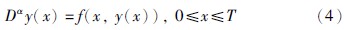
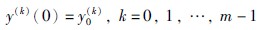
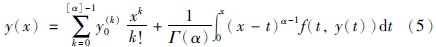
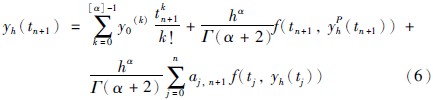
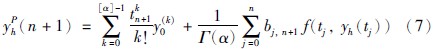
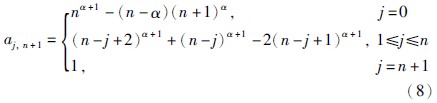
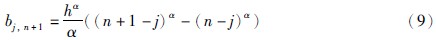
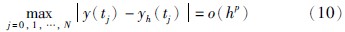
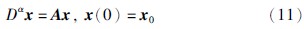
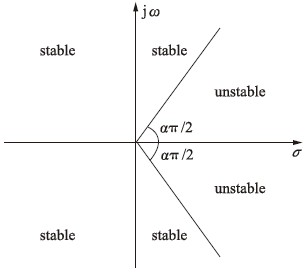
图 1 α阶线性系统的稳定区域Fig. 1 Stability region of linear system with order α 
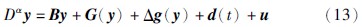
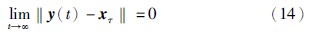
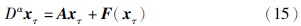
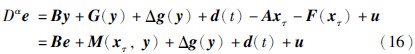
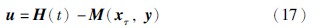
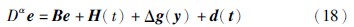

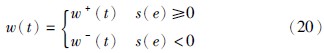
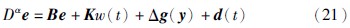


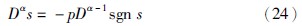
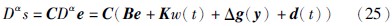
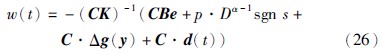
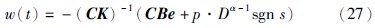
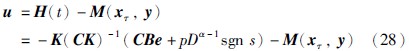

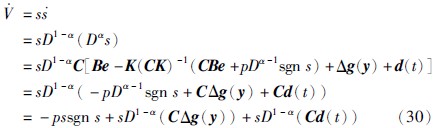
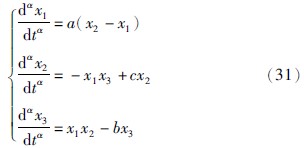
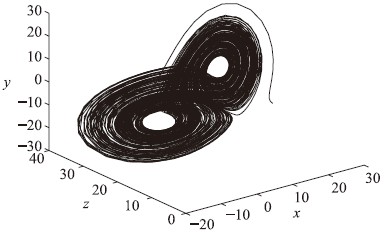
图 2 分数阶Lü系统的混沌吸引子(α=0.93)Fig. 2 Chaotic attractor of fractional-order Lü system (α=0.93) 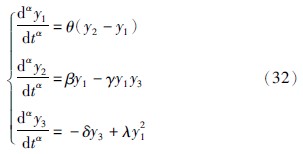
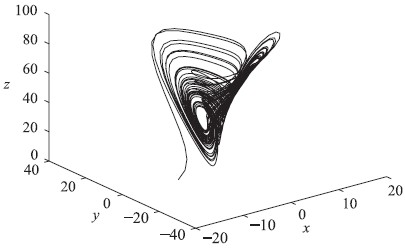
图 3 分数阶Liu系统的混沌吸引子(α=0.93)Fig. 3 Chaotic attractor of fractional-order Liu system (α=0.93) 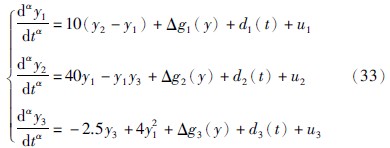
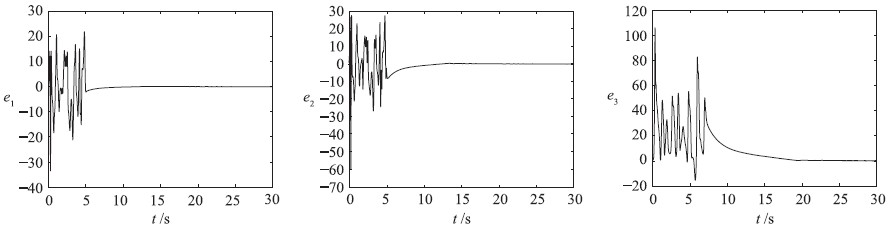
图 4 驱动系统(31)和响应系统(33)的延迟同步误差响应曲线Fig. 4 Lag synchronization errors response curves between drive system (31) and response system (33)
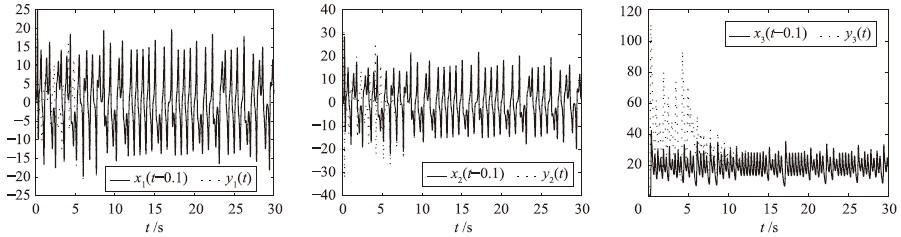
图 5 驱动系统(31)和响应系统(33)的状态同步轨迹(τ=0.1 s)Fig. 5 State synchronization trajectories between drive system (31) and response system (33) (τ=0.1 s) 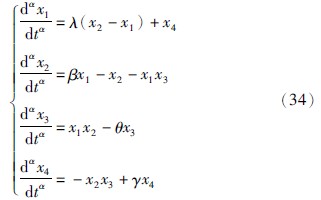
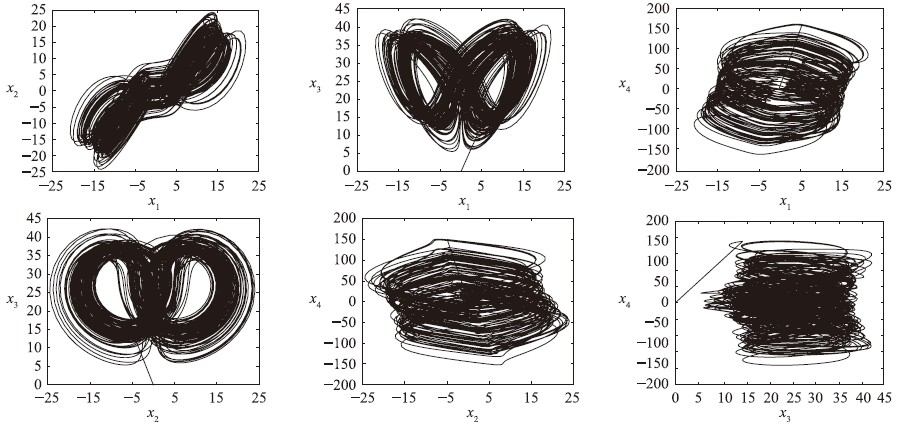
图 6 分数阶超混沌洛伦兹系统的混沌吸引子(α=0.98)Fig. 6 Chaotic attractor of fractional-order hyperchaotic Lorenz system (α=0.98) 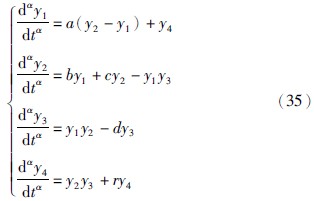
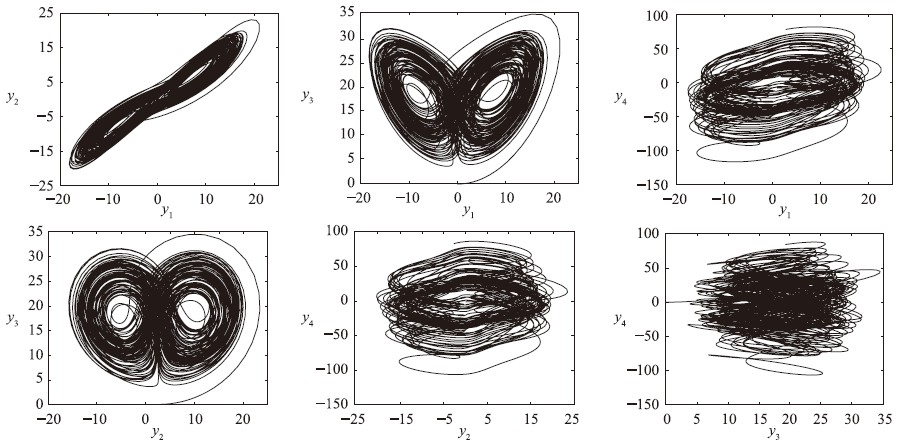
图 7 分数阶超混沌Chen系统的混沌吸引子(α=0.98)Fig. 7 Chaotic attractor of fractional-order hyperchaotic Chen system (α=0.98) 
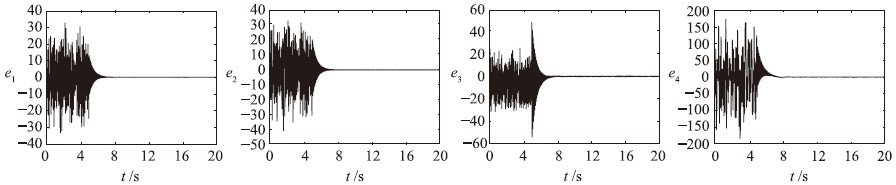
图 8 驱动系统(34)和响应系统(36)的延迟同步误差响应曲线Fig. 8 Lag synchronization errors response curves between drive system (34) and response system (36)
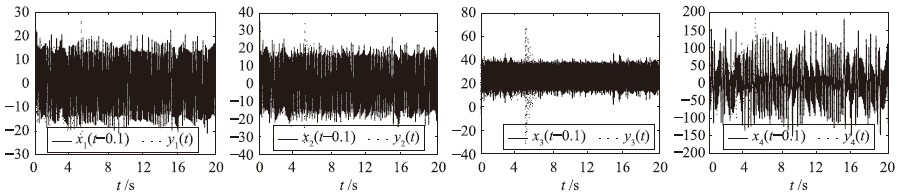
图 9 驱动系统(34)和响应系统(36)的状态同步轨迹(τ=0.1 s)Fig. 9 State synchronization trajectories between drive system (34) and response system (36) (τ=0.1 s)
| [1] | Pecora L M, Carroll T L. Synchronization in chaotic systems[J]. Physical Review Letters, 1990, 64(8): 821-824. |
| [2] | Rosenblum M G, Pikovsky A S, Kurths J. Phase synchronization of chaotic oscillators[J]. Physical Review Letters, 1996, 76(11): 1804-1807. |
| [3] | Shahverdiev E M, Sivaprakasam S, Shore K A. Lag synchronization in time-delayed systems[J]. Physics Letters A, 2002, 292(1): 320-324. |
| [4] | Li C, Liao X, Wong K. Lag synchronization of hyperchaos with application to secure communications[J]. Chaos, Solitons & Fractals, 2005, 23(1): 183-193. |
| [5] | Yang S S, Duan C K. Generalized synchronization in chaotic systems[J]. Chaos, Solitons & Fractals, 1998, 9(10): 1703-1707. |
| [6] | Mainieri R, Rehacek J. Projective synchronization in three-dimensional chaotic systems[J]. Physical Review Letters, 1999, 82(15): 3042-3045. |
| [7] | Zhang Q J, Lu J A. Full state hybrid lag projective synchronization in chaotic (hyperchaotic) systems[J]. Physics Letters A, 2008, 372(9): 1416-1421. |
| [8] | Li C P, Peng G J. Chaos in Chen′s system with a fractional order[J]. Chaos, Solitons & Fractals, 2004, 22(2): 443-450. |
| [9] | Grigorenko I, Grigorenko E. Chaotic Dynamics of the fractional Lorenz system[J]. Physical Review Letters, 2003, 91(3): 034101. |
| [10] | Ge Z M, Ou C Y. Chaos in a fractional order modified Duffing system[J]. Chaos, Solitons & Fractals, 2007, 34(2): 262-291. |
| [11] | Wang X Y, Wang M J. Dynamic analysis of the fractional-order Liu system and its synchronization[J]. Chaos, 2007, 17(3): 033106. |
| [12] | Lu J G. Chaotic dynamics of the fractional-order Lü system and its synchronization[J]. Physics Letters A, 2006, 354(4): 305-311. |
| [13] | Wu X J, Lu Y. Generalized projective synchronization of the fractional-order Chen hyperchaotic system[J]. Nonlinear Dynamics, 2009, 57(1/2): 25-35. |
| [14] | Wang T S, Wang X Y. Genearalized synchronization of fractional order hyperchaotic Lorenz system[J]. Modern Physics Letters B, 2009, 23(12): 2167-2178. |
| [15] | Li C G, Liao X F, Yu J B. Synchronization of fractional order chaotic systems[J]. Physical Review E, 2003, 68(6): 067203. |
| [16] | Bhalekar S, Gejji V D. Synchronization of different fractional order chaotic systems using active control[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(11): 3536-3546. |
| [17] | Hosseinnia S H, Ghaderi R, Ranjbar N A, et al. Sliding mode synchronization of an uncertain fractional order chaotic system[J]. Computers and Mathematics with Applications, 2010, 59(5): 1637-1643. |
| [18] | Xin B G, Chen T, Liu Y Q. Projective synchronization of chaotic fractional-order energy resources demand-supply systems via linear control [J]. Communications in Nonlinear Sciences and Numerical Simulations, 2011, 16(11): 4479-4486. |
| [19] | Zhou P, Ding R. Chaotic synchronization between different fractional-order chaotic systems[J]. Journal of the Franklin Institute, 2011, 348(10): 2839-2848. |
| [20] | Chen L P, Chai Y, Wu R C. Lag projective synchronization in fractional-order chaotic (hyperchaotic) systems[J]. Physics Letters A, 2011, 375(11): 2099-2110. |
| [21] | Mohammad P A. Robust stabilization and synchronization of a class of fractional-order chaotic systems via a novel fractional sliding mode controller[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 6(17): 2670-2681. |
| [22] | Si G Q, Sun Z Y, Zhang Y B, et al. Projective synchronization of different fractional-order chaotic systems with non-identical orders[J]. Nonlinear Analysis: Real World Applications, 2012, 4(13): 1761-1771. |
| [23] | Podlubny I. Fractional Differential Equations[M]. New York, USA: Academic Press, 1999. |
| [24] | Charef A, Sun H H, Tsao Y Y, et al. Fractal system as represented by singularity function[J]. IEEE Transactions on Automatic Control, 1992, 37(9): 1465-1470. |
| [25] | Ahmad W M, Sprott J C. Chaos in fractional-order autonomous nonlinear systems[J]. Chaos, Solitons & Fractals, 2003, 16(2): 339-351. |
| [26] | Diethelm K, Ford N J, Freed A D. A predictor-corrector approach for the numerical solution of fractional differential equations[J]. Nonlinear Dynamics, 2002, 29(1/2/3/4): 3-22. |
| [27] | Diethelm K. An algorithm for the numerical solution of differential equations of fractional order[J]. Electronic Transactions on Numerical Analysis, 1997, 5(1): 1-6. |
| [28] | Diethelm K, Ford N J, Freed A D. Detailed error analysis for a fractional Adams method[J]. Numerical Algorithms, 2004, 36(1): 31-52. |
| [29] | He J H. A new approach to nonlinear partial differential equations[J]. Communications in Nonlinear Science and Numerical Simulation, 1997, 2(4): 230-235. |
| [30] | Matignon D. Stability results on fractional differential equations with applications to control processing[C]//Proceedings of the IEEE Computation Engineering in System and Application Multiconference. Piscataway, NJ, USA: IEEE, 1996: 963-968. |
| [31] | Ahmed E, El-Sayed A M A, El-Saka H A A. Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models[J]. Journal of Mathematical Analysis and Applications, 2007, 325(1): 542-553. |



