1 引言
综合电力系统舰船[1, 2]、 大功率雷达等设备通常由柴油发电机组供电. 不同于陆地无穷大电力系统,由柴油发电机组和用电设备构成的独立电力系统容量有限,容易受到随机性和冲击性负载的影响,具有较强的非线性,因此,柴油发电机组的控制性能,对于保证受电设备的工作性能具有重要意义. 文[3, 4, 5]分析了不同类型发电机组的特点,并建立了相应的数学模型; 文[6, 7, 8, 9]采用反演设计、 H∞控制、 滑模变结构等方法对柴油发电机组的非线性励磁控制进行了研究; 文[10, 11]对柴油发电机组的非线性速度控制进行了研究; 文[12]通过数学推导和仿真验证的方法证明了柴油发电机组的励磁控制和速度控制是相互影响的,因此,非常有必要采用励磁和速度综合控制,以提高柴油发电机组的供电性能. 文[13, 14, 15, 16]采用Hamilton、 非线性H2/H∞等方法对励磁和速度综合控制进行了研究,但Hamilton、 非线性H2/H∞在研究过程中通常不考虑参数不确定性问题[17].
本文针对一类由交叉子系统构成的多输入非线性系统,提出了一种分散非线性自适应L2增益控制(nonlinear adaptive decentralized L2-gain control,NADC-L2)新方法,并将该新方法应用到了文[3]建立的励磁及机电复合调速控制中,进行了仿真验证试验,仿真结果表明: 采用新提出的NADC-L2既能保证电压、 转速双重稳定,也能够有效抑制外部干扰,提高发电机组的暂态稳定性.
2 非线性自适应分散L2增益控制原理 2.1 互联多输入系统描述本文分析的一类互联多输入系统由m个单输入系统构成,其中第i个子系统可表示为
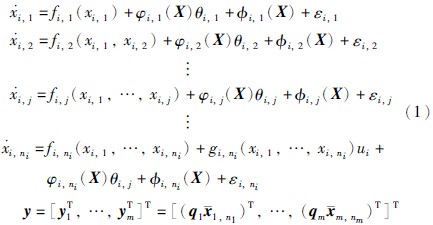
其中: xi,j(1≤j≤ni)表示第i个子系统的状态变量; X=[T1,n1,…,Tm,nm]T∈RN表示整个系统的状态变量; N=n1+…+nm; Tj,nj=[xj,1,…,xj,nj]T∈Rnj,j=1,…,m; u∈R为输入变量; φi,j(X)θi,j为不确定项,其中φi,j(X)包含第i个子系统与其它子系统的交叉项,且φi,j(0)=0; fi,j,gi,j,ϕi,j,j=1,2,…,ni是光滑函数,且满足fi,j(0)=0,gi,j(xi,1,…,xi,j)≠0; ϕi,j(X)包含第i个子系统与其它子系统的交叉项,且满足ϕi,j(0)=0; εi,j为随机扰动量,且满足εi,j∈L2=εi,j(t)∫t0ε2i,j(t)dt<∞,L2指有限能量信号集合; y为评价信号; qj(1≤j≤m)为加权对角矩阵.
假设1 在φi,j(X)和ϕi,j(X)中,第i个子系统与其它子系统间的交叉项可以在子系统i中作为整体量直接测量得到.
2.2 NADC-L2的实现第1步 取ei,1=xi,1,由式(1)得:
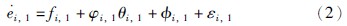
将式(2)代入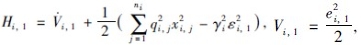 ,得:
,得:
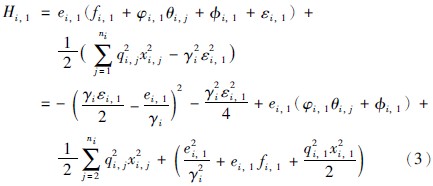
取虚拟控制x*i,2为
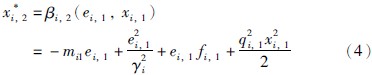
其中: mi1=fi1(|ei,1|)+ci1,fi1(ei,1)为有关ei,1的K类函数,ci1>0.
取ei,2=xi,2-x*i,2,由式(4)得:
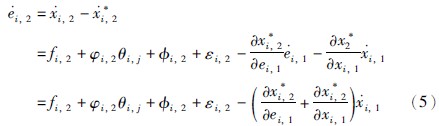
第2步 将式(3)、 式(5)代入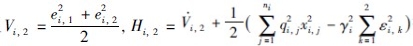 得:
得:
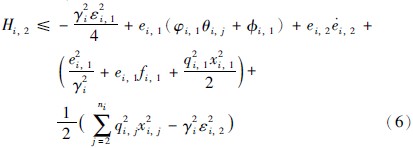
将式(5)代入式(6)得:
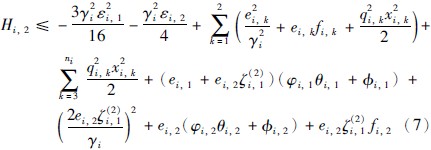
其中: 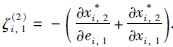 .
.
取虚拟控制x*i,3为
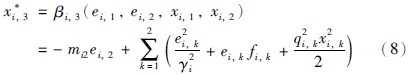
其中: mi2=fi2(ei,2)+ci2,fi2(ei,2)为有关ei,2的K类函数,ci2>0.
由式(8)得:
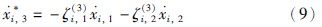
其中: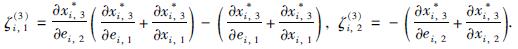
第3步 取Hi,3=Hi,2+ei,3i,3-γ2iε2i,32,由式(7)得:
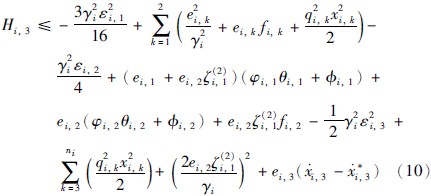
将式(9)代入式(10)得:
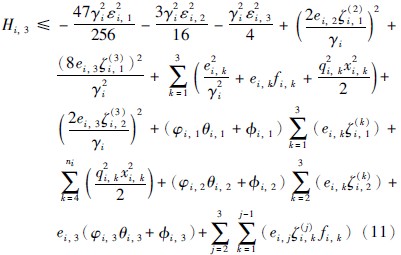
其中,ζ(1)i,1=ζ(2)i,2=ζ(3)i,3=1.
取虚拟控制x*i,4为
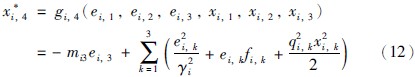
其中: mi3=fi3(ei,3)+ci3,fi3(ei,3)为有关ei,3的K类函数,ci3>0.
第m步 取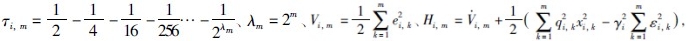 ,由
,由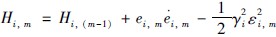 得:
得:
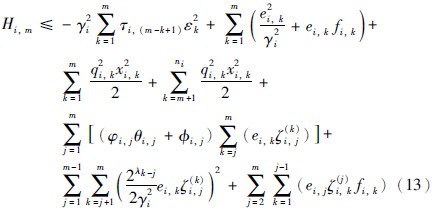
取虚拟控制x*i,m+1为
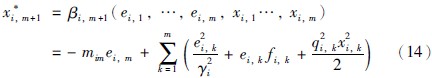
其中: mim=fim(ei,m)+cim,fim(ei,m)为有关ei,m的K类函数,cim>0.
由式(14)得以下递推式(15):
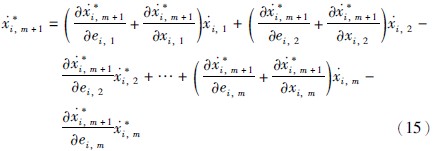
由式(15)得:
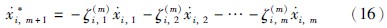
第n步 取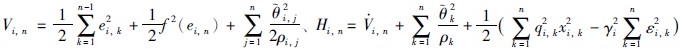 ,前n-1步中,取
,前n-1步中,取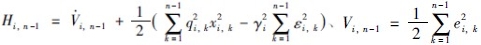 得:
得:

其中: 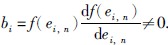 .
.
将通用式(13)代入式(17)得:
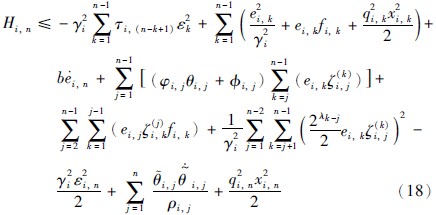


将式(19)、 式(20)代入式(18)得:
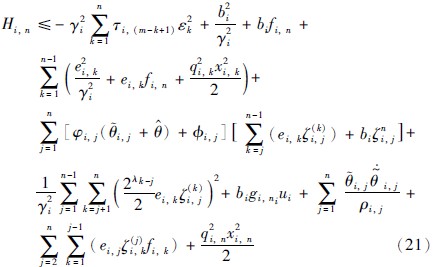
取参数自适应律和控制律分别为
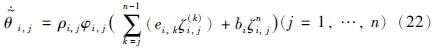
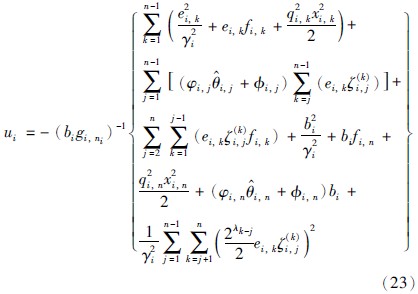
将式(22)、 式(23)代入式(21)得:
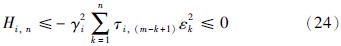
由于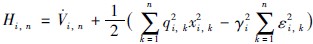 ,所以由式(24)得
,所以由式(24)得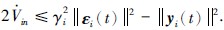 ,则有:
,则有:
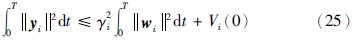
定理 式(22)、 式(23)可实现系统(1)各子系统的分散L2增益干扰抑制控制.
证明 定义系统(1)各子系统的存储函数为Vi(x)=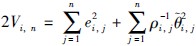 . 求存储函数沿系统(1)的导数,则在式(22)、 (23)作用下,满足
. 求存储函数沿系统(1)的导数,则在式(22)、 (23)作用下,满足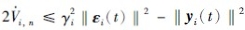 ,并求积分可得
,并求积分可得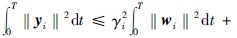 Vi(0). 因此,式(22)、 (23)可实现系统(1)各子系统的L2增益干扰抑制控制.
Vi(0). 因此,式(22)、 (23)可实现系统(1)各子系统的L2增益干扰抑制控制.
评价1 NADC-L2方法在实现各子系统L2增益干扰抑制控制的基础上,保证了多输入系统(1)的整体干扰抑制,因此,具有分散控制的特性. 多输入系统(1)的存储函数为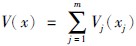 .
.
评价2 NADC-L2给出了一类非严参数块反馈的多输入系统的规律性L2增益抑制计算公式,克服了传统L2增益抑制设计过程中反复递推计算的不足.
3 柴油发电机组NADC-L2文[3]建立的机电复合调速模型可表示为

其中: x1=y为调速套移动距离增量; x2=
=z为调速套移动速度; x3=L为执行器移动距离增量; u1为电磁执行器的驱动控制; 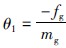 与调速套的摩擦系数有关,为不确定参数;
与调速套的摩擦系数有关,为不确定参数; 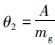 为飞块儿对调速套向右支持力对调速套位移的偏导,受飞块儿张开角度的影响为不确定参数; θ3=
为飞块儿对调速套向右支持力对调速套位移的偏导,受飞块儿张开角度的影响为不确定参数; θ3=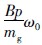 为飞块儿对调速套向右支持力对飞块儿转动速度的偏导,为不确定参数;
为飞块儿对调速套向右支持力对飞块儿转动速度的偏导,为不确定参数; 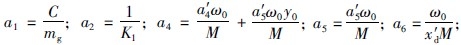 ; ε1代表由系统模型误差和调速套滑动抖动等引起的外部干扰; ε2代表执行器控制电压中的电磁等外部干扰; x5=ω-1代表发电机电角速度增量的标幺值; θ4=-D2H与阻尼系数D相关,为不确定系数; ε3代表扭矩干扰.
; ε1代表由系统模型误差和调速套滑动抖动等引起的外部干扰; ε2代表执行器控制电压中的电磁等外部干扰; x5=ω-1代表发电机电角速度增量的标幺值; θ4=-D2H与阻尼系数D相关,为不确定系数; ε3代表扭矩干扰.
由文[3]知,同步发电机满足转子运动方程(26d)、 功角—转速方程(26e)和励磁绕组电磁暂态方程(26f):


其中: x4=δ为发电机的功角增量; x6=Eq′(t)为q轴空载暂态电势增量; 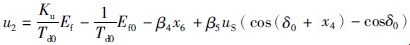 为预反馈励磁控制,Ef为励磁控制输入,Id为直轴电流,Td0′为暂态励磁绕组时间常数,xd为直轴电抗,xd′为直轴暂态电抗; ε4为励磁绕组上的外部电磁干扰.
为预反馈励磁控制,Ef为励磁控制输入,Id为直轴电流,Td0′为暂态励磁绕组时间常数,xd为直轴电抗,xd′为直轴暂态电抗; ε4为励磁绕组上的外部电磁干扰.
当取系统的输出为y=[q3x3,q4x4,q5x5]T时,系统(26)的L2增益干扰抑制即: 通过设计控制律(u1、 u2)和参数自适应律(θ ^1、 θ ^2、 θ ^3、 θ ^4)实现干扰ε=[ε1,ε2,ε3,ε4]T到输出y增益小于γ.
系统(26)由两个子系统Sys(1)和Sys(2)构成. Sys(1)由(26a)、 (26b)和(26c)组成,Sys(2)由(26d)、 (26e)和(26f)组成. 两个子系统之间的交叉项为x5=ω/ω0,且ω可以测量得到,因此x5满足可以直接测量获得的要求. 由于Sys(1)和Sys(2)均具有非线性系统模型式(1)的结构,因此,可采用2.2节方法对两个交叉互联子系统进行NADC-L2设计,具体步骤如下:
3.1 Sys(1)的非线性鲁棒自适应控制取e1=x1,得1=x2.
取V1=e212、 H1=V·1+q23x232,得H1=e1x1+q23x232.
取x*2=-m1e1、 e2=x2-x*2,由式(26b)得:
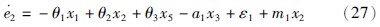
取V2=e21+e222、 H2=V·2+q23x232-γ2ε212,由式(27)得:
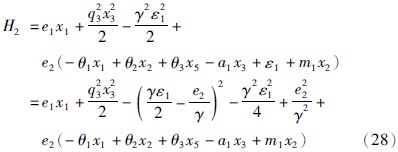
取虚拟控制x*3=-m2e2+e22γ2,得:
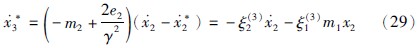
其中: ξ(3)2=ξ(3)1=m2-2e2γ2.
取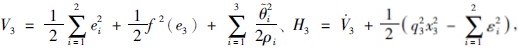 依据H2的定义可得:
依据H2的定义可得:
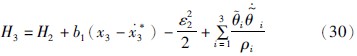
其中: 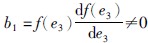 .
.
将式(26)、 式(27)代入式(30)得:
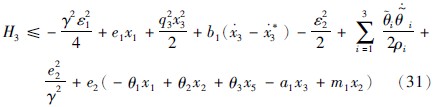
将式(29)代入式(31)得式(32):
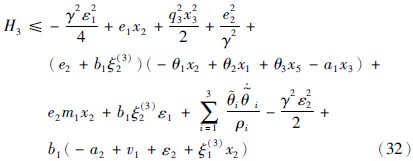
由式(32)化简得下式(33):
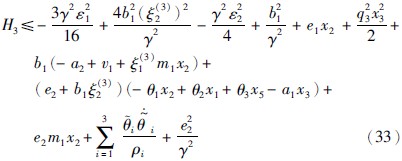
由式(33)得参数自适应律和控制律分别为



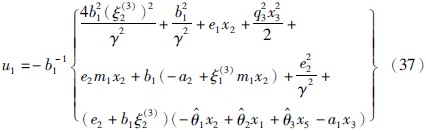
将式(34)~(37)代入式(33)得:
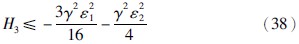
取e4=x4,得4=x5.
取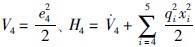 ,得
,得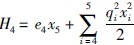 .
.
取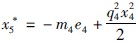 ,得:
,得:
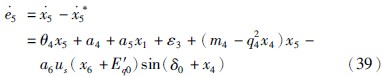
取V5=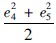 、
、 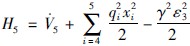 ,将式(39)代入H5得:
,将式(39)代入H5得:
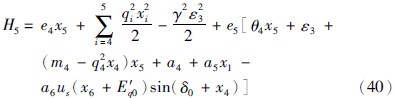
由式(40)得:
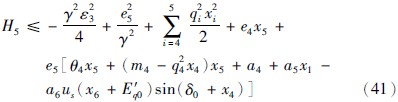
取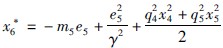 ,得:
,得:
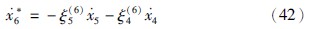
其中: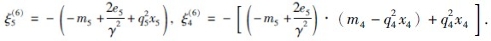
取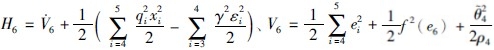 ,将式(41)、 (42)代入H6得:
,将式(41)、 (42)代入H6得:
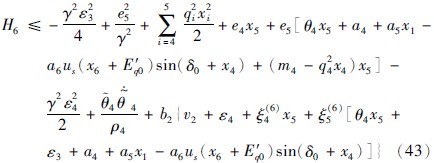
其中: 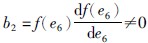
由式(43)得:
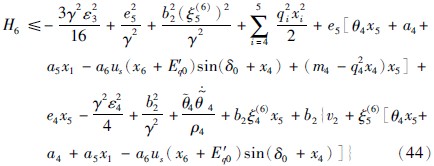
由式(44)得参数自适应律(45)和控制律(46):

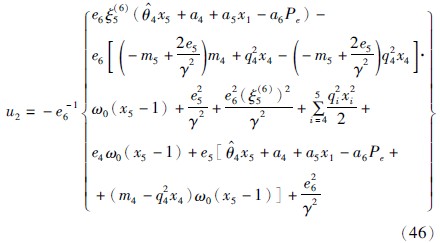
将式(45)、 式(46)代入式(44)得:
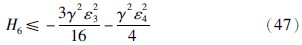
定理 采用式(34)~(37)、 (45)和(46)可实现系统(26)的非线性自适应L2增益控制.
证明 取存储函数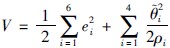 ,定义函数
,定义函数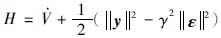 ,当参数自适应律为(34)~(36)和(45)、 控制律为(37)和(46)时,由式(27)~(47)知
,当参数自适应律为(34)~(36)和(45)、 控制律为(37)和(46)时,由式(27)~(47)知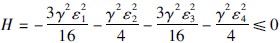 ,从而可得:
,从而可得: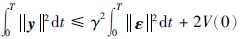 ,因此,式(34)~(37)、 (45)和(46)可实现机电复合调速型柴油发电机组的非线性自适应L2增益干扰抑制. 证毕.
,因此,式(34)~(37)、 (45)和(46)可实现机电复合调速型柴油发电机组的非线性自适应L2增益干扰抑制. 证毕.
以文[3]建立的机电复合调速、 三次谐波励磁的移动电站模型为对象,对所提控制方法进行仿真验证和分析. 仿真中,模型的相关参数如下: a1=1.2,a2=3,a4=4.2,a5=1.6,a6=0.2,xd=1.25(标幺值),xd′=0.221,xd=1.25(标幺值),Td0′=1.05 s,H=3.2 s,干扰抑制常数γ=2.
4.1 采用常规非线性鲁棒自适应控制的励磁及转速综合控制采用常规非线性鲁棒自适应控制,即式(34)~(37)、 (45)和(46)中m1=3、 m2=2、 m4=5、 m5=6、 b1=1+2e3+sin e3、 b2=1+2e6+sin e6、 ρ1=ρ2=ρ3=ρ4=3为常数,在第2.5 s突增50%额定负载时,柴油发电机组的转速ω、 端电压Vt以及控制输入的动态变化曲线如图 1所示.
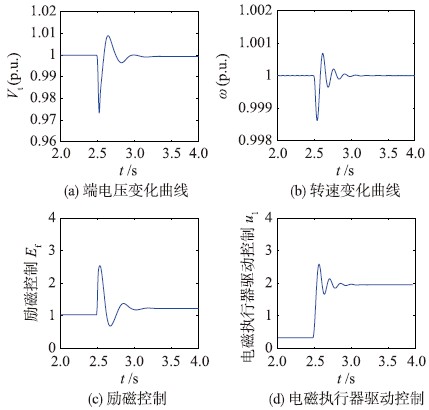 |
| 图 1 不含K类函数时的NADC-L2控制曲线Fig. 1 Curves of NADC-L2 without K-class functions |
当虚拟控制控制变量中的参数mi为常数时,本文所提NADC-L2方法将退变为常规非线性鲁棒自适应控制,仿真图形表明,退变后的NADC-L2同样可以实现一类非线性系统的L2增益干扰抑制控制.
4.2 含K类函数NADC-L2的励磁及转速综合控制引入K类函数后,取式(34)~(37)、 (45)和(46)中的m1=3+3e21、 m2=2+2e22、 m4=5+5e24、 m5=6+6e25、 b1=1+2e3+sine3、 b2=1+2e6+sine6、 ρ1=ρ2=3、 ρ3=ρ4=3,仍然在第2.1 s突然增加50%额定负载时,柴油发电机组的转速ω、 端电压Vt以及控制输入的动态变化曲线如图 2所示.
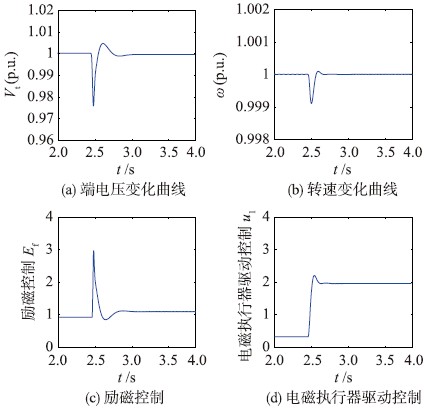 |
| 图 2 引入K类函数后的NADC-L2控制曲线Fig. 2 Curves of NADC-L2 with K-class functions |
图 1、 图 2对比表明: 采用新的NADC-L2控制后,端电压和转速的稳定时间由原来的1.2 s缩短到了0.9 s左右,端电压和转速的震荡次数由原来的3次减少为了2次,速度的下降幅度明显减小,相对于传统的非线性鲁棒自适应控制方法,新提出的NADC-L2可以提高状态变量的收敛速度,增强L2增益控制能力. 其中主要原因是新提出的NADC-L2引入了K类函数,使得当误差变量ei增加时,控制变量ui的值也将增大,控制作用增强.
5 结论本文针对柴油发电机组励磁及速度综合L2增益控制设计困难的难题,提出了一种新的NADC-L2设计方法. 该方法可以广泛应用于一类互联多输入系统的分散L2增益控制. 以具体发电机组为对象,进行了仿真验证,仿真结果表明: 当存在外部干扰时,相对于传统L2增益控制,新方法由于引入了K类函数,因此在误差较大时,控制作用增强,所以新的NADC-L2方法能够加快发电机组端电压和转速的收敛速度,对于提高发电机组的暂态稳定性具有重要意义.
| [1] | 王淼, 戴剑锋, 周双喜, 等. 全电力推进船舶电力系统的数字仿真[J]. 电工技术学报, 2006, 21(4): 62-67. Wang M, Dai J F, Zhou S X, et al. Digital simulation of ship power system with electric propulsion[J]. Transactions of China Electrotechnical Society, 2006, 21(4): 62-67. |
| [2] | 马伟明. 电力电子在舰船电力系统中的典型应用[J]. 电工技术学报, 2011, 26(5): 1-6. Ma W M. Typical applications of power electronics in naval ship power systems[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 1-6. |
| [3] | 谷志锋, 朱长青, 赵文杰, 等. 谐波励磁机电复合调速型移动电站特性研究[J]. 内燃机工程, 2013, 34(5): 87-92. Gu Z F, Zhu C Q, Zhao W J, et al. Research on the characters of the harmonic exciting and mechanical and electrical speed controlling power station[J]. Chinese Internal Combustion Engine Engineering, 2013, 34(5): 87-92. |
| [4] | 黄曼磊, 王常虹. 船舶电站柴油发电机组的非线性数学模型[J]. 哈尔滨工程大学学报, 2006, 27(1): 15-20. Huang M L, Wang C H. Nonlinear mathematical model of diesel-generator set on ship[J]. Journal of Harbin Engineering University, 2006, 27(1): 15-20. |
| [5] | 孙军, 钱阳军, 路平, 等. 柴油机机电复合式调速系统的研究[J]. 内燃机工程, 1998, 19(1): 11-17. Sun J, Qian Y J, Lu P, et al. Research on mechanical-electronic governing system for disel engine[J]. Chinese Internal Combustion Engine Engineering, 1998, 19(1): 11-17. |
| [6] | 谷志锋, 朱长青, 邵天章, 等. 全状态参数最优控制的鲁棒自适应励磁控制[J]. 控制理论与应用, 2013, 30(7): 856-862. Gu Z F, Zhu C Q, Shao T Z, et al. Robust adaptive control for the excitation system based on total-state-parameter optimum control[J]. Control Theory & Applications, 2013, 30(7): 856-862. |
| [7] | 黄曼磊. 船舶电站同步发电机H∞调压器的仿真研究[J]. 哈尔滨工程大学学报, 2004, 25(2): 162-166. Huang M L. Simulation research on H∞voltage regulator for synchronous generator of a ship power station[J]. Journal of Harbin Engineering University, 2004, 25(2): 162-166. |
| [8] | 葛友, 李春文. H∞滑模鲁棒励磁控制器设计[J]. 中国电机工程学报, 2002, 22(5): 1-4. Ge Y, Li C W. Design for H∞sliding mode robust excitation controller[J]. Proceedings of the CSEE, 2002, 22(5): 1-4. |
| [9] | 刘辉, 李啸骢, 韦化. 基于目标全息反馈法的发电机非线性励磁控制设计[J]. 中国电机工程学报, 2007, 27(1): 14-18. Liu H, Li X C, Wei H. Nonlinear excitation control for generator unit based on NCOHF[J]. Proceedings of the CSEE, 2007, 27(1): 14-18. |
| [10] | 黄曼磊, 宋克明, 魏志达. 柴油发电机组非线性H2/H∞调速器的研究[J]. 控制理论与应用, 2009, 26(8): 873-878. Huang M L, Song K M, Wei Z D. Nonlinear H2/H∞speed regulator for a diesel-generator set[J]. Control Theory & Applications, 2009, 26(8): 873-878. |
| [11] | 黄曼磊, 王常虹. 船舶电站柴油机非线性H∞调速器[J]. 电工技术学报, 2006, 21(10): 56-61. Huang M L, Wang C H. Nonlinear H∞governor for diesel engine of ship power station[J]. Transactions of China Electro-technical Society, 2006, 21(10): 56-61. |
| [12] | 谷志锋, 朱长青, 赵文杰, 等. 励磁系统参数对发电机组力矩特性的影响[J]. 中国机械工程, 2013, 24(18): 2448-2451. Gu Z F, Zhu C Q, Zhao W J, et al. Influence of excitation system parameters on moment characteristics of generator set[J]. China Mechanical Engineering, 2013, 24(18): 2448-2451. |
| [13] | 张利军, 孟杰, 兰海. 基于Hamilton函数方法的船舶发电机组综合协调控制[J]. 控制理论与应用, 2011, 28(11): 1541-1548. Zhang L J, Meng J, Lan H. Integrated coordination control of marine generators based on Hamilton function approach[J]. Control Theory & Applications, 2011, 28(11): 1541-1548. |
| [14] | 黄曼磊, 宋克明, 魏志达. 柴油发电机组非线性H2/H∞综合控制器[J]. 控制理论与应用, 2011, 28(6): 885-893. Huang M L, Song K M, Wei Z D. Nonlinear H2/H∞synthetic controller for diesel-generator set[J]. Control Theory & Application, 2011, 28(6): 885-893. |
| [15] | 黄曼磊, 王常虹. 船舶电站柴油机非线性H∞调速器[J]. 电工技术学报, 2006, 21(10): 56-61. Huang M L, Wang C H. Nonlinear H∞governor for diesel engine of ship power station[J]. Transactions of China Electrotechnical Society, 2006, 21(10): 56-61. |
| [16] | 谷志锋, 朱长青, 张晨光, 等. 双重强跟踪滤波励磁及速度非线性鲁棒控制[J]. 控制理论与应用, 2014, 31(1): 85-92. Gu Z F, Zhu C Q, Zhang C G, et al. Nonlinear robust excitation and speed control based on the double strong tracking filter[J]. Control Theory & Applications, 2014, 31(1): 85-92. |
| [17] | 李果, 王辉. 汽车转向/防抱死制动系统的非线性鲁棒协调控制[J]. 信息与控制, 2012, 41(2): 256-261. Li G, Wang H. The nonlinear robust coordinated control of the steering/anti-lock braking system of the vehicles[J]. Information and Control, 2012, 41(2): 256-261. |



