1 引言
现代战场单部雷达很难应对电子干扰、 低空/超低空突防、 高速反辐射导弹和隐身飞机四大威胁，多雷达组网是行之有效的解决途径，它以多部组网雷达为探测数据源，具有较高的对空探测数据率，具备对空域机动目标有效跟踪的数据率优势[1, 2, 3]，其核心和关键为数据融合处理[4, 5, 6]. 同时，使用单一、 固定的模型很难准确描述高速高机动目标的所有可能运动状态，而使用多个模型组合描述目标运动状态是有效的解决办法，即交互多模型(interacting mutiple model，IMM)算法[7, 8]. 本文将交互多模型算法与卡尔曼滤波器结合使用，跟踪强机动目标. 卡尔曼滤波(Kalman filter，KF)[9, 10, 11]为线性、 高斯噪声条件下的最优估计方法. 而在多雷达组网系统中，组网雷达测量值为极坐标条件下的斜距、 方位角和仰角，目标跟踪状态为融合中心直角坐标系值，测量值与跟踪状态为非线性关系，不满足卡尔曼滤波线性化要求. 针对此类问题，工程上有两种解决方案： (1) 使用扩展卡尔曼滤波(extended Kalman filter，EKF)算法[12, 13]； (2) 将跟踪坐标系虚拟为滤波器观测坐标系. EKF算法使用局部线性化方法来截取状态方程(或观测方程)的泰勒级数展开1阶项，实现非线性方程的近似线性化. 这种局部线性化方法以牺牲高阶项为代价，必然影响目标跟踪滤波精度. 虚拟观测方法，通过组网坐标变换技术，将组网雷达探测点迹直接变换至融合中心直角坐标系，形成虚拟观测值，使得虚拟观测与目标状态间呈线性关系，满足卡尔曼滤波线性化要求. 一般认为，在真实的观测坐标系中，观测分量相互独立，观测噪声服从高斯白噪声分布. 但组网虚拟观测坐标系并非真实的观测坐标系，并不满足观测分量相互独立性要求，也很难满足高斯白噪声随机分布特性要求. 但文[4]指出，在确知噪声分布2阶矩信息条件下，卡尔曼滤波仍为最优估计. 本文基于雷达测量噪声特性分析，通过虚拟观测协方差建模、 初始化建模，构建虚拟观测卡尔曼滤波(virtual observation Kalman filter，VOKF)，结合交互多模型算法，构造交互多模型虚拟观测卡尔曼滤波算法(IMM-VOKFA)，用于解决多雷达组网对空域机动目标的有效滤波跟踪，期望提升多雷达组网工程化水平.
2 虚拟观测噪声建模本文将组网融合中心惯性坐标系虚拟为滤波器观测坐标系，涉及滤波器递推使用的观测协方差矩阵，无法直接构造，需要针对雷达组网噪声来源，并结合雷达组网系统的坐标变换特性来研究解决.
2.1 组网雷达极坐标系与惯性坐标系变换关系令当前k时刻空域目标T组网雷达极坐标为[rk，θk，ϕk]T(斜距、 方位角、 仰角)，目标T雷达惯性坐标为[xrkyrkzrk]T，两者变换关系[14]为
雷达惯性坐标系变换至融合中心惯性坐标系过程，包括旋转和平移两种坐标变换操作的复合[15]，令目标T的融合中心惯性坐标为[xfkyfkzfk]T，则：
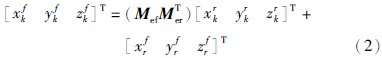
其中[xfryfrzfr]T为组网雷达的融合中心惯性坐标，Mef、 Mer分别为地心惯性坐标系至融合中心惯性坐标系、 雷达惯性坐标系旋转变换矩阵[15].
2.3 组网雷达惯性坐标误差统计特性分析由式(1)可知，不考虑坐标变换误差因素，目标T的组网雷达惯性坐标误差产生于组网雷达的极坐标测量误差，则测量误差引起的组网雷达惯性坐标误差为
其中，E(·)为期望值.
工程上一般认为，雷达测量误差服从均值为0、 方差δ2r、 δ2θ和δ2ϕ独立的高斯分布，因此，式(3)所示的雷达惯性坐标误差均值为0，即：
则组网雷达惯性坐标误差2阶中心矩解析式如式(5)～(9)所示：
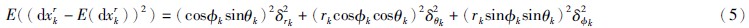
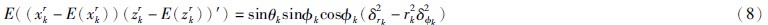
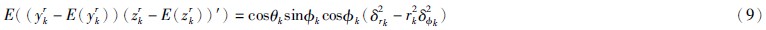
可以看出，由测量噪声产生的组网雷达惯性坐标误差，在惯性坐标系各轴向分量上互相关联耦合，在滤波跟踪时，必须充分考虑这一特性.
2.4 融合中心惯性坐标误差统计特性分析根据式(2)的组网坐标变换关系，不考虑坐标变换误差因素，基于组网雷达测量噪声影响，计算融合中心惯性坐标误差，并取数学期望：
基于组网雷达测量噪声影响，计算融合中心惯性坐标误差的2阶中心矩：
其为组网雷达惯性坐标2阶中心矩的线性组合，各轴向上互相关联耦合.
2.5 虚拟观测噪声建模虚拟观测坐标系即融合中心惯性坐标系，从观测角度来看，其为在各分量方向上的“观测噪声”，即为组网雷达测量噪声因素作用下的融合中心惯性坐标误差，因此，式(11)的融合中心惯性坐标误差2阶中心矩即是虚拟观测协方差矩阵Rk.
3 多雷达组网交互多模型虚拟观测卡尔曼滤波状态估计建模针对多雷达组网系统特点，本文拟选用3个模型构造交互多模型组，即匀速直线运动(CV)模型、 逆时针协同转弯(ACT)模型和顺时针协同转弯(CCT)模型.
3.1 虚拟观测卡尔曼滤波状态/观测建模IMM-VOKFA的3种模型的状态方程和测量方程表达式如式(12)、 (13)所示：
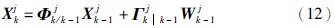
其中，模型序号j=1，2，3，Vjk为虚拟观测噪声，其统计特性为虚拟观测协方差矩阵Rk，对于CV、 ACT和CCT模型，式(12)和式(13)中的参量分别见文[15, 16, 17].
3.2 多模型滤波初始交互建模IMM-VOKFA用于雷达组网目标状态滤波估计时，针对每个测量点迹更新，模型组成员均参与滤波估计，需要重新计算模型成员的初始状态和协方差估计，即基于模型成员前一时刻滤波估计、 状态转移、 模型混合概率综合计算实现：
其中，r为模型数目，X^ik-1、 Pik-1为模型成员i在k-1时刻状态估计和协方差，μijk-1为模型混合概率：
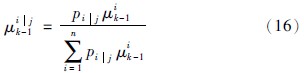
其中，μik-1、 μi0分别为前一时刻、 初始时刻模型概率，pij为模型转移概率.
3.3 虚拟卡尔曼滤波航迹初始化建模本文只估计空域机动目标在融合中心坐标系x轴和y轴方向的运动位置和速度，因此，与模型j相匹配的VOKFA初始化采用两点差分法，利用航迹起始的第1、 2时刻的测量值，来确定VOKFA的初始状态估计和估计误差协方差矩阵：
令Z1′=[x1′f，y1′f]T、 Z2′=[x2′f，y2′f]T，分别表示第1、 2时刻组网雷达虚拟观测值，则初始状态估计值X^i0为
令
和
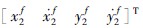为第1、 2时刻的目标状态真值，则目标状态真值和虚拟观测值的关系式为
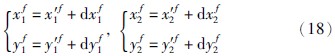
其中，[dxf1dyf1]T、 [dxf2dyf2]T分别为第1、 2时刻的目标位置真值与虚拟观测值误差，则VOKFA初始估计误差为
计算VOKFA初始估计误差协方差矩阵：
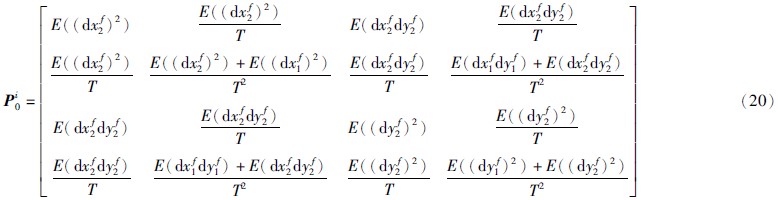
其中，E((dxf1)2)、 E((dxf2)2)、 E((dyf1)2)、 E((dyf2)2)分别为第1时刻和第2时刻虚拟观测误差方差，E(dxf1dyf1)、 E(dxf2dyf2)为对应的互协方差.
3.4 多模型虚拟卡尔曼滤波计算流程根据文[9, 10, 11]可知，VOKFA用于多雷达组网对空域机动目标滤波跟踪，其流程如式(21)～(25)所示：
基于模型的残差信息计算模型j的似然函数Λjk：
其中，
为模型j的VOKFA残差，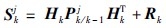
为残差协方差，m是测量值的维数. 根据贝叶斯法则，k时刻模型j的模型概率为
基于模型组成员的状态估计经加权得到目标的状态估计及其协方差：
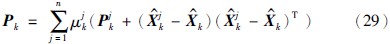
为了验证本文算法的有效性与实用性，采用Matlab软件仿真的方法来测试验证. 仿真硬件环境为： Pentium(R) Dual-Core CPU，HP E5200，主频2.5 GHz，内存2.00 G. 仿真场景如下： 组网雷达2部，分别为雷达1和雷达2，其扫描周期T为10 s； 雷达1的距离精度为130 m，方位角精度为0.3°，俯仰角精度为0.2°，配置位置为[118° 32° 40 m]T； 雷达2的距离精度为90 m，方位角精度为0.2°，俯仰角精度为0.1°，配置位置为[119° 30.5° 140 m]T. 融合中心的配置位置为[119° 32° 192 m]T. 为了验证计算的简便性，特别假定2组网雷达对目标进行等间隔探测，融合中心每5 s收到1个探测采样点，全程共300个采样点迹，设目标航迹模型采用CV模型1、 CT模型2和CT模型3，前500 s做匀速直线运动，然后做角速度为0.007 rad/s的逆时针转弯运动500 s，再以角速度-0.007 rad/s做顺时针转弯运动500 s，全程飞行高度8 000 m不变. 为了克服随机因素影响，进行100次仿真统计计算.
仿真初始化(1) 飞行起点位置为[118.5° 31° 8 000 m]T，航速200 m/s，飞行航向角50°；
(2) 马尔可夫转移概率：
状态噪声σx=0.8，σy=0.8；
(3) 初始模型概率：
μ0=[0.95+0.05/30.05/30.05/3]T
(4) 与CV模型1、 CT模型2、 3匹配的初始状态都计算为
初始估计协方差矩阵：
初始观测协方差矩阵：
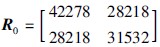
图 1为两部雷达组网仿真场景，图 2包括目标IMM-VOKFA位置估计值、 真值点迹和测量点迹三种仿真值，放在同一图中以进行对比. 从图 2可以看出，目标真实轨迹是先做匀速直线运动，然后做逆时针转弯运动，最后转换为顺时针转弯运动，估计轨迹能够逼近真实轨迹，目标真实运动模型变换时是瞬间变化，但IMM-VOKFA能迅速跟踪到目标，证明了IMM-VOKFA所建立模型的有效性.
 |
| 图 1 多雷达组网仿真测试场景Fig. 1 Test scenarios of multi-radar networking simulation |
 |
| 图 2 IMM-VOKFA位置估计点迹与噪声化点迹VS真实点迹对比Fig. 2 Comparison among the estimated position plots by IMM-VOKFA，noise plots and true plots |
图 3和图 4是IMM-VOKFA位置估计在X、 Y方向与目标真实位置绝对误差曲线，图 5和图 6是IMM-EKFA位置估计在X、 Y方向与目标真实位置绝对误差曲线，可以看出，本文提出的IMM-VOKFA收敛性很好，没有较大的初始波动. 由于组网雷达测量噪声影响，测量点迹对比真值，波动较大，IMM-VOKFA估计误差较小，估计精度较高，真值逼近度较高； IMM-VOKFA的机动自适应性较好，尽管在目标机动转弯处，估计误差有些起伏波动，但波动幅度不大，波动时间不长，能够快速趋于平稳. 工程上扩展卡尔曼滤波算法(EKFA)常用于估计非线性系统，本文仿真中，同样条件下IMM-VOKFA位置估计误差明显小于IMM-EKFA，且IMM-EKFA估计在266点后滤波发散，可见本文IMM-VOKFA明显优于IMM-EKFA.
 |
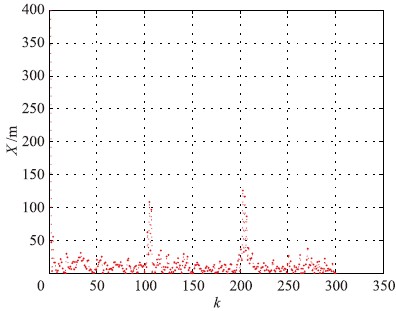| 图 3 IMM-VOKFA位置估计误差曲线(X方向)，X方向估计均方根误差为56 mFig. 3 IMM-VOKFA error curve of the position estimation (X direction)，where the root mean square error in X direction is 56 m |
 |
| 图 4 IMM-VOKFA位置估计误差曲线(Y方向)，Y方向估计均方根误差为15 mFig. 4 IMM-VOKFA error curve of the position estimation (Y direction)，where the root mean square error in Y direction is 15 m |
 |
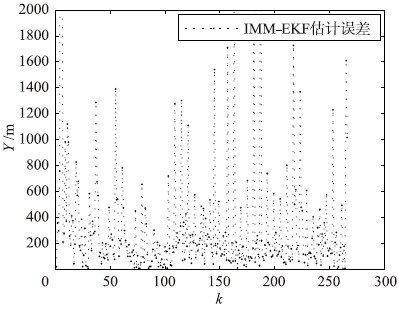| 图 5 IMM-EKF位置估计误差曲线(X方向)，X方向估计均方根误差为71 mFig. 5 IMM-EKF error curve of the position estimation (X direction)，where the root mean square error in X direction is 71 m |
 |
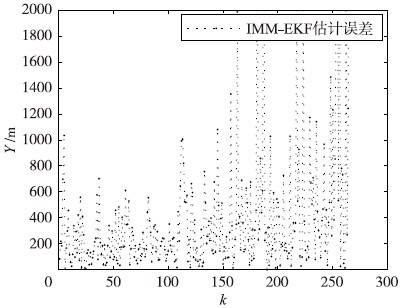| 图 6 IMM-EKF位置估计误差曲线(Y方向)，Y方向估计均方根误差为83 mFig. 6 IMM-EKF error curve of the position estimation (Y direction)，where the root mean square error in Y direction is 83 m |
图 7为算法测试的模型概率变化情况，可以看出，IMM-VOKFA能够自适应地选择接近实际运动的模型，无需机动判别处理，模型自适应性较强.
 |
| 图 7 模型概率变化曲线Fig. 7 Curves of model probability changes |
总的来看，基于交互多模型结合虚拟观测卡尔曼滤波构造的IMM-VOKFA，X方向估计均方根误差是56 m，Y方向是15 m，估计精度高，模型准确概率达到0.9以上，模型机动自适用性好，能够用于多雷达组网对空域机动目标的滤波跟踪.
| [1] | 赵艳丽, 陈永光, 蒙洁, 等. 分布式组网雷达抗多假目标欺骗干扰处理方法[J]. 电光与控制, 2011, 18(3): 25-30. Zhao Y L, Chen Y G, Meng J, et al. A data processing method against multi-false-target deception jamming for distributed radar network[J]. Electronics Optics ＆ Control, 2011, 18(3): 25-30. |
| [2] | 杨跃轮, 李洪梅. 分布式干扰下雷达组网探测效能分析[J]. 指挥控制与仿真, 2012, 34(3): 41-43, 66. Yang Y L, Li H M. Analysis of radar nets′ operational effectiveness on the condition of distributed jammers[J]. Command Control ＆ Simulation, 2012, 34(3): 41-43, 66. |
| [3] | 韩晓威. 雷达组网显控技术研究[J]. 现代导航, 2011(5): 367-370. Han X W. Study on radar nets′ display and control technology[J]. Modern Navigation, 2011(5): 367-370. |
| [4] | Hall D L, Llines J. 多传感器数据融合手册[M]. 北京: 电子工业出版社, 2008: 1-70, 382-388. Hall D L, Llines J. Handbook of multisensor data fusion[M]. Beijing: Publishing House of Electronics Industry, 2008: 1-70, 382-388. |
| [5] | 方青. 雷达组网数据融合处理中的点迹融合技术[J]. 现代电子, 2002(4): 5-12. Fang Q. Plot fusion technology in radar network data fusion[J]. Modern Electronics, 2002(4): 5-12. |
| [6] | 叶丽丽. 多雷达点迹融合技术研究[D]. 西安: 西安电子科技大学, 2009. Ye L L. Study on multi-radars plot fusion technology[D]. Xi′an: Xidian University, 2009. |
| [7] | Blom H A, Bar-Shalom Y. The interacting multiple model algorithm for systems with Markovian switching coefficients[J]. IEEE Transactions on Automatic Control, 1988, 33(8): 780-783. |
| [8] | 谈顺成, 王国宏, 王娜. IMM-Singer模型的机动目标跟踪算法[J]. 火力控制与指挥, 2012, 37(2): 32-34. Tan S C, Wang G H, Wang N. Maneuvering target tracking algorithm based on IMM-Singer model[J]. Fire Control ＆ Command Control, 2012, 37(2): 32-34. |
| [9] | Kalman R E. A new approach to linear filter and prediction problems[J]. Transactions of the ASME-Journal of Basic Enginearing, 1960, 82(1): 34-45. |
| [10] | Yang Y F. Comparison of linearized Kalinan filter and extended Kalman filter for satellite motion states estimation[J]. Journal of Measurement Science and Instrumentation, 2011, 2(4): 307-311. |
| [11] | Xiong K, Liang T, Lei Y J. Multiple model Kalman filter for attitude determination of precision pointing spacecraft[J]. Acta Astronautica, 2011, 68(7): 843-852. |
| [12] | Wang Z, Liu X, Liu Y, et al. An extended Kalman filtering approach to modeling nonlinear dynamic gene regulatory networks via short gene expression time series[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2009, 6(3): 410-419. |
| [13] | Huang G P, Trawny N, Mourikis A I, et al. Observability-based consistent EKF estimators for multi-robot cooperative localization[J]. Autonomous Robots, 2011, 30(1): 99-122. |
| [14] | 赵温波, 都基焱. 组网雷达噪声惯性坐标系误差统计特性研究[J]. 炮兵学院学报, 2010(5): 91-95. Zhao W B, Du J Y. Study on noise statistical properties of radar network in inertial coordinate system[J]. Journal of Artillery College, 2010(5): 91-95. |
| [15] | Zhou H R, Jing Z L, Wang P D. Tracking of maneuvering targets[M]. Beijing: National Defense Industry Press, 1991: 1-55. |
| [16] | Han C Z, Zhu H Y, Duan Z S. Multi-source information fusion[M]. Beijing: Tsinghua University Press, 2010: 142-154. |
| [17] | 王华楠, 刘高峰, 顾雪峰. 自适应转弯模型的交互多模型算法研究[J]. 弹箭与制导学报, 2008, 28(5): 241-245. Wang H N, Liu G F, Gu X F. Research on adaptive turning model in grid multiple model algorithm[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(5): 241-245. |