1 引言
基于证据推理的置信规则库推理方法[1](belief rule-base inference methodology using the evidential reasoning approach,RIMER)是在D-S证据理论[2, 3]、 决策理论[4]、 模糊理论[5]和传统IF-THEN规则库[6]的基础上发展而来,具有处理多种不同不确定信息的能力. 由于其在处理不确定性多属性决策问题中具有明显的优势,目前以RIMER为核心的置信规则库(belief rule base,BRB)系统已成功地应用于工程系统安全评估[7]、 石墨成分检测[8]、 管线检漏[9]等领域.
置信规则库是进行RIMER推理的基础,因此构建一个健壮的置信规则库能够提高BRB系统决策的准确性,然而,在构建置信规则库时需要覆盖所有前提属性及每个属性的候选值,致使置信规则库中的规则数呈指数量级的趋势增长,当实际问题过于复杂时,易引发“组合爆炸”问题[10]. 目前国内外学者针对该问题所提出的方法主要是通过调整前提属性和候选值的数量来达到降低规则库规模的目的: 对于前提属性数量是固定的,但候选值数量未知的情况,周志杰[11, 12]提出了统计效用的概念来评价各规则,最终仅保留统计效用值达到一定阈值的规则; 对于前提属性数量是可变的情况,常雷雷[13]引入灰靶(grey target,GT)、 多维尺度(multi-dimensional scaling,MDS)、 等距映射(Isomap)、 主成分分析(principal component analysis,PCA)等传统维度约简[14]的方法,通过对专家信息的处理来筛选重要的前提属性,并依此重构置信规则库. 上述的规则约简方法都已被证实能够明显地精简置信规则库,但综合分析发现这些方法仍存在不足,例如GT、 MDS等方法虽然精简了置信规则库但无法保证BRB系统推理的准确性; 而Isomap、 PCA等方法虽然约简规则数量和推理准确性都比较理想但前者涉及复杂的算法,计算复杂度较高且不易实现,后者则在筛选关键属性时存在一定的局限性. 为健全现有的规则约简方法,本文从多属性决策问题中赋权方法的角度提出了一种新的规则约简方法,相比于传统的维度约简方法,利用赋权方法进行规则约简的实质是将计算所得的属性权重作为筛选关键属性的标准.
本文所提出的新的规则约简方法是基于赋权方法中的关联系数标准差[15](correlation coefficient and standard deviation integrated method,CCSD)法,该权重确定方法的核心思想是逐个将待考察属性移除,以计算多属性决策问题的综合评价值,即各属性的权重. 由于权重计算方式与规则约简时移除前提属性相类似,因此属性权重的权值大小可直观地反映出约简前提属性后对置信规则库推理准确性产生的影响. 在基于CCSD的规则约简方法的具体实验分析中,以装甲装备体系综合能力评估的置信规则库作为分析实例,首先对各前提属性的关联权重的计算结果作简要的说明,并将基于CCSD的规则约简方法与现有规则约简方法进行比较; 最后在以特殊方案和一般方案两种情形作为实例输入时,分析关联权重的权值大小与BRB系统决策准确性间存在的关系.
2 RIMER方法及问题描述RIMER方法主要分成三大部分,分别是构建置信规则库、 计算激活权重和利用证据推理(evidential reasoning,ER)算法合成激活规则,其中置信规则库的构建需要遍历所有的前提属性及每个属性的候选值,因此当前提属性数量过多时容易引起“组合爆炸”问题,目前针对该问题的解决方法多为基于维度约简的规则约简方法.
2.1 置信规则库的表示置信规则库是由传统的IF-THEN规则库发展而来,通过引入置信框架,使原来的IF-THEN规则能够合理地表示含有不确定信息的知识,完善后的规则称为置信规则,其表示形式如下:
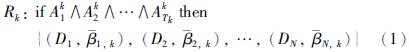
该置信规则中还包含有两个重要的参数,即规则权重θk和前提属性权重集合δ={δk,1,δk,2,…,δk,Tk; k=1,…,L},Tk表示第k条置信规则中前提属性的数量,L表示置信规则库中置信规则的总条数,此外,在式(1)中Aki表示在第k条置信规则中第i个前提属性的候选值,j,k表示在第k条置信规则中结果集对于第j个评价等级Dj的置信度. 如果∑Ni=1i,k=1,则称表示的信息是完整的,否则称表示的信息是不完整的.
2.2 BRB系统的推理过程BRB系统是以RIMER算法为核心,在RIMER算法中包含计算激活权重、 结果集置信度的修正和利用ER算法合成激活规则3个部分,而由RIMER算法推理所得的置信度分布为BRB系统的常见输出类型之一.
2.2.1 激活权重的计算激活权重的计算取决于输入数据、 前提属性权重和规则权重,因此置信规则库中第k条规则的激活权重计算公式可表示为
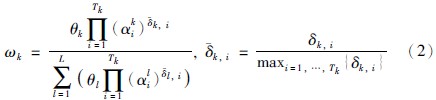
上式中αki表示第k条规则中第i个前提属性的输入数据转换而得的个体匹配度,其中当规则权重为零时,激活权重也为零,此时,当前激活规则对BRB系统的决策结果不起任何影响.
2.2.2 结果集置信度的修正由于输入数据可能不完全,因此被激活规则结果集的置信度需要做进一步修正,则在第k条规则的结果集中第i个等级上的置信度修正公式如下:
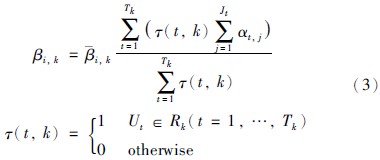
由式(2)、 式(3)可求得全部激活规则的激活权重及修正的结果集置信度,每条被激活的规则可视为ER方法中的一个基本属性,因此可用ER算法[16]将所有激活规则进行合成,由每个基本属性的置信度和属性权重可以求得基本属性的基本可信值:
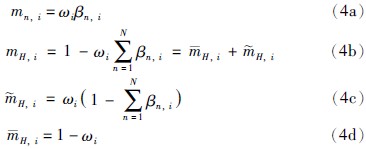
上式中n=1,…,N,i=1,…,L. 在基本可信值的基础上利用解析公式[17]可将所有的基本属性一次合成,合成公式为
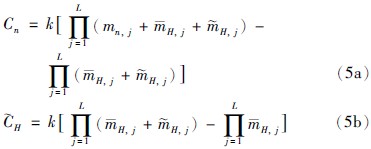
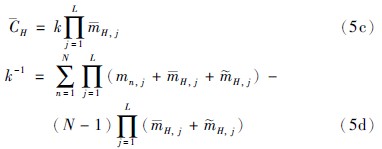
最后可求得综合属性的置信度:
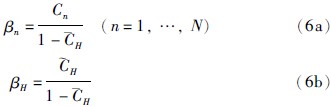
由ER算法合成激活规则后得到的置信度是BRB系统的常见输出类型之一,其中第i个置信规则库相关的置信度分布输出可表示为
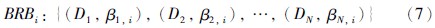
当BRB系统的输入要求为简单的数值类型时,可将置信度分布转化为平均效用值,假设N个评价等级的等级效用值满足: μ1≤μ2≤…≤μN,则第i个置信规则库的平均效用值计算公式可表示为
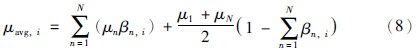
在不同的BRB系统中,对于相同的输入数据由其推理所得的置信度分布可能并不相同,为了比较彼此间的差异,本文引入相似度的计算公式,假设有两个置信规则库BRBi和BRBj,则在两个置信规则库上推理所得的置信度分布的相似程度可表示如下:
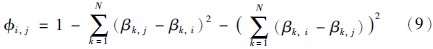
置信规则库的构建需要覆盖所有的前提属性及每个属性的候选值,因此当置信规则库中总共有T个前提属性,且第i个前提属性的候选值个数为Ji时,则置信规则库中规则数可达 =1Ji,例如当前提属性的个数为5,每个前提属性候选值的个数均为3时,那么所构建置信规则库的置信规则数为35=243条,显然,置信规则库中的置信规则数是一个指数量级的规模,因此当问题过于复杂时容易引起“组合爆炸”问题,解决该问题最直接、 有效的方式是减少前提属性的个数,这是因为在置信规则库中,并非每一个前提属性都是必不可少的,通过筛选关键的前提属性来重建置信规则库可以有效地缩减置信规则库中的规则数,这些关键的前提属性也可以被称为关键性能参数[18].
=1Ji,例如当前提属性的个数为5,每个前提属性候选值的个数均为3时,那么所构建置信规则库的置信规则数为35=243条,显然,置信规则库中的置信规则数是一个指数量级的规模,因此当问题过于复杂时容易引起“组合爆炸”问题,解决该问题最直接、 有效的方式是减少前提属性的个数,这是因为在置信规则库中,并非每一个前提属性都是必不可少的,通过筛选关键的前提属性来重建置信规则库可以有效地缩减置信规则库中的规则数,这些关键的前提属性也可以被称为关键性能参数[18].
针对置信规则库的“组合爆炸”问题,现有的解决方法多为基于维度约简的规则约简方法,包括有GT、 Isomap、 MDS及PCA等方法,文[13]从规则约简数量、 置信度分布、 最大置信度及方差等方面对各方法进行比较,最终得出Isomap与PCA约简方法的约简效果最为理想,具体分析这两种方法,Isomap约简方法主要是应用Isomap非线性降维算法,该算法需要3个步骤来实现: 首先标记相邻节点及计算相邻图,然后应用Dijkstra算法或Floyd算法计算流形上各点的测地线距离,最后再应用MDS算法找出嵌入在高维空间的低维坐标. 由上述算法步骤可知,Isomap算法是以MDS算法为基础,通过用流形上两点间测地距离取代MDS算法中的欧氏距离来提升维度约简的准确性,但该改进却使算法的计算复杂度明显增大. 再分析PCA约简方法,其主要是应用PCA线性降维算法,在规则约简时首先应用奇异值分解法求解评价矩阵的成分,然后选取特征值大于1或累计比例达到80%以上的前k个成分求解载荷矩阵,并用最大四次方值法对载荷矩阵进行旋转,最后再选取旋转后各成分载荷的绝对值大于0.8的前提属性作为关键属性. 经对上述算法的最后一步分析不难发现在筛选关键属性的方式上存在一定的局限性.
为了形象说明现有方法的不足,以下从实验分析的角度剖析Isomap与PCA约简方法. 假设在置信规则库中有T个前提属性,每个前提属性允许专家使用的评价等级个数为P,则可以构建一个T×TP的评价矩阵,即需要计算TP个节点间的最短距离,因此当前提属性个数或评价等级个数增加时用于计算两点间最短距离的时间开销呈指数增长的趋势. 由此可见,Isomap约简方法虽然约简规则数量和推理准确性都比较理想但方法涉及复杂的算法,计算复杂度较高且不易实现. 对于PCA约简方法,首先分析选择特征值大于1的前k个成分作为主成分时的情形,由文[13]中的分析可知,由关键属性重构的置信规则库的推理准确性并非最佳; 再分析选择特征值累计比例达到80%以上的前k个成分作为主成分的情形,假设选取前5个成分作为主成分,其特征值累计比例为100%,则旋转后的载荷矩阵如表 1所示.
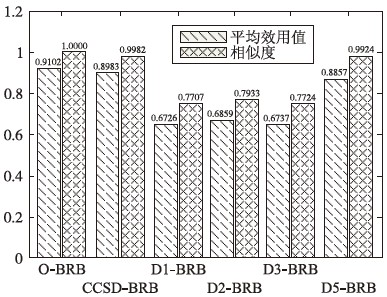
| 前提属性名称 | 主成分 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 指控 | 0.978 | 0.037 | -0.054 | 0.030 | -0.198 |
| 机动性 | -0.054 | 0.060 | 0.959 | -0.241 | -0.123 |
| 火力 | 0.031 | -0.165 | -0.260 | 0.939 | 0.148 |
| 防御力 | -0.239 | -0.202 | -0.140 | 0.157 | 0.926 |
| 通讯 | 0.039 | 0.971 | 0.059 | -0.148 | -0.173 |
由表 1可知,当选取各成分载荷的绝对值大于0.8的前提属性作为关键属性时,5个前提属性均符合要求,由于不存在非关键属性,因此无法缩减置信规则库中的规则数. 上述的情形中PCA约简方法均无法保证约简效果,主要原因在于筛选关键属性时仅考虑前提属性对主成分的贡献程度,而忽略了各主成分间的相对重要性. 由此可见,PCA约简方法虽然在个例中约简规则数量和推理准确性都比较理想,但方法在筛选关键属性时存在局限性,因此其适用性有待进一步验证.
3 基于赋权方法的BRB规则约简方法随着国内外学者对置信规则库中“组合爆炸”问题认知的加深,用于置信规则库规则约简的方法相继被提出,但这些方法主要是建立在传统维度约简方法[14]的基础上,方法的适用性有待进一步研究. 为了健全现有的规则约简方法,本文从多属性决策问题中赋权方法的角度提出规则约简的新方法. 在本节中首先对赋权方法作简要的概述,然后介绍基于关联系数标准差的规则约简方法.
3.1 赋权方法与规则约简赋权方法是针对多属性决策问题而归纳的用于确定各个属性权重的方法,由于属性权重是决策信息中的重要信息之一,因此有关赋权方法的研究受到了广泛的重视. 目前,赋权方法可分成三类: 主观型、 客观型和综合型,其中主观型是依据决策者主观偏好确定权重的方法,包括有: 相对比较法、 连环比率法、 德尔菲法(Delphi)、 集值迭代法、 最小平方法、 特征向量法、 简单多属性排序法(SMART,SMARTER)和SWING等[19, 20]. 客观型是利用已知的客观决策矩阵信息来决定权重的方法,包括: 熵值法、 标准差赋权法(SD)、 逼近理想点法和关联系数标准差法等[19]. 综合型则是结合主观信息和客观决策矩阵信息来计算权重的方法,主要有: 加法集成、 乘法集成、 分类赋权法和“广义拉开档次”赋权法等[21].
由于现有的赋权方法种类繁多,且由赋权方法确定的权重可近似特征提取的结果,因此本文将赋权方法引入到置信规则库的规则约简中. 属性权重的大小与其对决策结果影响程度的大小存在正相关,即: 当属性对决策的影响程度越小时,计算所得的权重越小,反之,权重越大. 所以在规则约简时首先利用赋权方法计算各前提属性的权重,然后根据权重的大小筛选出前k个所对应的前提属性作为关键属性,最后再使用关键属性重构规模缩减的置信规则库.
3.2 基于CCSD的规则约简方法关联系数标准差法是客观型赋权方法,其思想是通过整合每个属性的标准差与总体评价值的关联系数来计算属性的权值,其中总体评价值的关联系数是指属性被移除时的总体评价值与该属性未被移除时的总体评价值的关联度. 由于在权重计算中移除属性的方式与规则约简时约简非关键属性相类似,因此本文选择采用基于关联系数标准差提出置信规则库的规则约简方法,为了与置信规则库中固有的前提属性权重进行区分,本文称关联系数标准差方法计算所得的权重为关联权重. 在基于CCSD的规则约简方法中由于关联权重的计算是算法的核心步骤,以下将首先对关联权重的计算作具体介绍,然后在此基础上再介绍基于CCSD的规则约简方法的算法步骤. 为方便叙述,称基于CCSD的规则约简方法为CCSD约简方法.
3.2.1 关联权重的计算首先,利用专家知识或先验数据对每个前提属性做出评价,假设前提属性的数量是T,评价信息共有N组,则评价信息可用矩阵形式表示,称为评价矩阵.
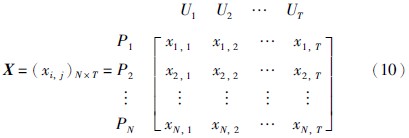
由于评价矩阵中各个评价信息在表示时属于有量纲的表示形式,因此需要将评价矩阵中的数值化为无量纲的表示形式,成为纯量,即对评价矩阵进行标准化处理; 同时,在转换时还需依据前提属性的性质,分别对其进行效益型和成本型的标准化,公式如下所示:
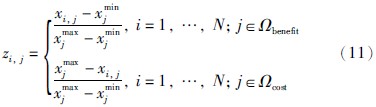
标准化后的评价矩阵表示如下:
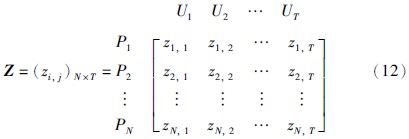
然后,初始化每个前提属性的关联权重W={ω1,ω2,…,ωT},初始化过程中需确保权重符合如下条件:
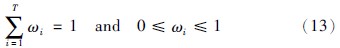
引入简单的加权方法,计算各个评价方案的总体评价值,计算公式表示如下:
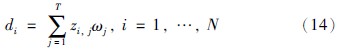
因此当移除某个前提属性后,当前各个评价方案的总体评价值的计算公式可修改为
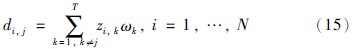
则前提属性Uj关于总体评价值的关联系数表示为
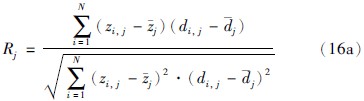
其中
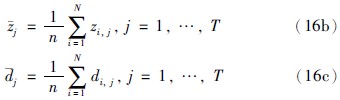
最后,可以依据前提属性间的标准差与关联系数求得前提属性的关联权重:
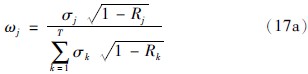
其中前提属性间的标准差的计算公式如下:
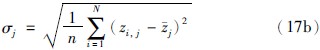
在上述关联权重的计算过程中不难发现,首先需要初始化前提属性的关联权重,然后依据前提属性间的标准差和关联系数再重新计算前提属性的关联权重,且求解关联权重的过程属于求解非线性等式的过程,因此为了简化求解过程,将求解关联权重的过程转换为求解如下优化模型的过程.
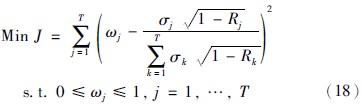
当优化模型求得最优解,即J=0时,所求得的W={ω1,ω2,…,ωT}即为各个前提属性的关联权重.
3.2.2 CCSD约简方法的算法步骤在关联权重的基础上,可将CCSD约简方法的算法步骤概述如下. 其中算法流程如图 1所示.
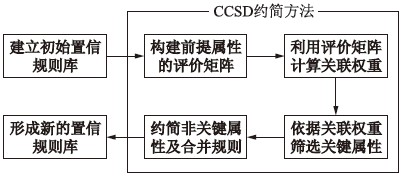 |
| 图 1 CCSD约简方法的流程Fig. 1 Flow of CCSD reduction method |
步骤1 依据现有的前提属性、 前提属性的候选值、 结果集的置信度分布建立初始的置信规则库.
步骤2 通过专家知识或历史数据分析各个前提属性间的强弱连接关系,并依此建立对各前提属性评价的评价矩阵.
步骤3 利用评价矩阵建立关于关联权重的非线性方程组,并通过求解方程组来计算各个前提属性的关联权重.
步骤4 依据关联权重选取权值大于特定阈值或前k大的前提属性作为关键属性.
步骤5 约简置信规则库中的非关键属性,并合并因前提属性被约简后产生的重复置信规则.
步骤6 重构精简的置信规则库,并将其作为BRB系统的新知识库.
上述算法步骤中,步骤2至步骤5即为CCSD约简方法约简置信规则库的主要算法流程,其中在步骤2中,目前国内外研究表明无论是德尔菲法或改良的专家评估方法都能有效地表示和集成专家知识,为CCSD约简方法中评价矩阵的构建提供充实的理论依据,并最终确保CCSD约简方法的准确性.
3.2.3 算法复杂度分析下面对所提算法的计算复杂度进行分析,以此说明新方法的良好计算性能. 在CCSD约简方法中,由算法的各个步骤可知其主要计算量是构建和求解关联权重的优化模型. 对于优化模型的构建,式(11)需要的时间代价为O(NT),式(15)为O(NT2),式(16)为O(NT+NT),式(17)为O(NT+T); 对于优化模型的求解,本文借助Matlab中的fmincon函数,该函数默认算法是trust-region-reglective算法,其依据给定的初始值来进行梯度步长的迭代求解,为了精简该部分时间复杂度的表示形式,令fmincon函数一次迭代求解的时间复杂度为O(F). 假设CCSD约简方法需要迭代M次才能求得关联权重,则CCSD约简方法的算法复杂度为
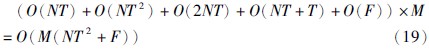
为了检验CCSD约简方法在实际应用中的适用性,本文引入装甲装备体系综合能力评估的置信规则库[13],其中该置信规则库主要用于验证现有规则约简方法的约简效果. 装甲装备体系综合能力评估的置信规则库中含5个前提属性,分别为“指令与控制”、 “机动性”、 “火力”、 “防御力”和“通讯”,如图 2所示. 假设每个前提属性的识别框架均为{A,B,C},由此可知装甲装备体系综合能力评估的置信规则库中共有规则数243条,具体参见文[13].
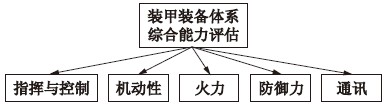 |
| 图 2 装甲装备体系综合能力评估模型Fig. 2 The evaluation model of the comprehensive capability for an armored system |
以下首先介绍CCSD约简方法如何应用于上述实例,并比较CCSD约简方法与现有规则约简方法的有效性,最后在特殊方案和一般方案中分析关联权重的权值大小与BRB系统决策准确性间的关系.
4.1 置信规则库的约简由于本文方法与现有规则约简方法的预处理过程相同,即在规则约简时需要通过专家知识对5个前提属性作出评估,为此本文使用已有的专家评估信息来确定前提属性间是否存在强连接关系,其中由专家确定的7个强连接关系[13]如下: 火力—防御力、 指挥与控制—通讯、 机动性—通讯、 指挥与控制—机动性、 指挥与控制—机动性—通讯、 指挥与控制—火力、 指挥与控制—火力—通讯.
为了构造前提属性的评价矩阵,提出如下3个假设[13]:
(1) 上述的7个强连接关系中,对于以下两种情况均不考虑: 1) 评价等级都为C的情况; 2) 评价等级中同时出现A和C的情况.
(2) 当分析任一强连接关系时,其余前提属性的评价信息均假设为A.
(3) 评价矩阵中的评价类型单独唯一,出现重复情况时,只保留一个.
经上述的3个假设可构建出由31组评价信息组成的评价矩阵,其中评价矩阵的转置如下所示:

为了将定性的评价等级合理地转换为定量的评价等级,引入互惠指数转换[22]的方法,转换数值如表 2所示.
| A | B | C | |
| 转化指标 | α0≈1 | α-2≈0.618 | α-4≈0.382 |
将定性的评价矩阵转换为定量的评价矩阵后,通过Matlab中的fmincon函数可求解各个前提属性的关联权重,如图 3所示.
 |
| 图 3 CCSD约简方法确定的关联权重Fig. 3 The correlation weight calculated by CCSD reduction method |
由图 3可知,在CCSD约简方法确定的关联权重中,依据权值的大小关系可将前提属性分成3个层次,其中第一层次由前提属性“指挥与控制”、 “机动性”和“火力”组成,前提属性间关联权重的最大差值为0.004 5; 第二层次由前提属性“通讯”组成,与第一层次中前提属性的最小关联权重差值为0.038 7,占前提属性“通讯”关联权重的比重为20.57%; 第三层次由前提属性“防御力”组成,与第二层次中前提属性的最小关联权重差值为0.078 4,占前提属性“防御力”关联权重的比重为71.42%. 由此可知,约简第三层次中前提属性“防御力”对BRB系统推理准确性产生的影响最小,而约简第一层次中前提属性将对BRB系统推理准确性产生的影响最大,具体的分析见4.3节.
4.2 有效性对比分析现有的规则约简方法中,Isomap与PCA约简方法的约简效果最为理想,因此,以下将主要对Isomap约简方法、 PCA约简方法及CCSD约简方法进行对比分析.
从方法的有效性比较各规则约简方法. 由Isomap和PCA约简方法筛选的关键属性为前提属性“指挥与控制”、 “机动性”、 “火力”和“通讯”,因此重构的置信规则库中规则数为34=81,考虑置信规则库中部分规则可以合并的原则,还可将置信规则库中规则数进一步降低到25条. 对比本文提出的CCSD约简方法,由各前提属性的关联权重可知,前提属性“防御力”的权值最低且与其它前提属性的关联权重差值较大,因此在约简非关键前提属性时,应首先约简前提属性“防御力”,由此可见,CCSD约简方法与Isomap和PCA约简方法重构的置信规则库完全相同,因此CCSD约简方法不仅能够有效地缩减置信规则库的规则数,同时还能保证BRB系统决策结果的准确性.
此外,对于CCSD约简方法,其核心思想是逐个将待考察属性移除,再通过标准差与总体评价值的关联系数来计算属性的关联权重. 由于权重的求解可转换为最优化问题,而在Matlab中具有功能强大的优化工具箱,因此在规则约简中仅需实现式(9)~(16),算法实现较为简单; 进一步分析关键属性的筛选方式,关联权重是在移除前提属性时计算的权重,而置信规则库中规则约简的本质同样是移除前提属性,因此依据前提属性间关联权重的权值大小来选取关键属性具有一定的合理性.
4.3 准确性对比分析为了客观地比较在约简不同关联权重的前提属性后对BRB系统推理准确性产生的影响,首先本文选取原置信规则库作为参照对象,同时还在原置信规则库的基础上分别约简前提属性“指令与控制”、 “机动性”、 “火力”、 “防御力”和“通讯”后构建的新置信规则库; 为方便叙述,以下称原置信规则库为O-BRB; 在O-BRB基础上分别约简“指令与控制”、 “机动性”、 “火力”和“通讯”后构建的置信规则库称为D1-BRB、 D2-BRB、 D3-BRB和D5-BRB,此外,由于前提属性“防御力”的关联权重最低,因此称约简“防御力”后新建的置信规则库为CCSD-BRB.
在准确性的分析中,本文从效用值和相似度两方面对比分析各置信规则库. 其中对于效用值的计算,假定识别框架中各个评价等级的等级效用值为
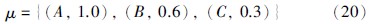
在上述假设的基础上,先以特殊方案P作为实例输入,方案P={(指令与控制=(A,0.8),(B,0.2)),(机动性=(A,0.7),(B,0.3)),(火力=(A,0.9),(B,0.1)),(防御力=(A,0.6),(B,0.4)),(通讯=(A,0.7),(B,0.3))}. 依据方案P在上述6个置信规则库中推理后,结果如图 3所示,则有相应的结论:
在效用值的对比分析中,CCSD-BRB上的平均效用值为0.898 3,相比于O-BRB上的平均效用值差值仅有0.011 9,该差值是所有约简后置信规则库与O-BRB在平均效用值上的最小偏差; 而在剩余的4个置信规则库中,平均效用值最接近O-BRB的置信规则库是D5-BRB,两者的平均效用值的差值为0.024 5,略大于CCSD-BRB与O-BRB间平均效用值的差值,因此从效用值的偏差程度不难发现约简关联权重越低的前提属性对平均效用值产生的影响越小.
在相似度的对比分析中,由相似度的计算公式可知,相似度反应规则库约简前后系统推理所得置信度分布的相似程度,而图中仅有CCSD-BRB和D5-BRB两者的相似度高于0.99,且明显大于其余3个置信规则库上的相似度,因此进一步证明依据前提属性间关联权重的大小来选取关键属性具有一定的合理性; 综上所述,在特殊方案中CCSD约简方法能够有效地保证BRB系统推理的准确性.
4.3.2 一般方案作为实例输入进一步验证用一般方案作为实例输入时,CCSD约简方法能够保证BRB系统决策的准确性,分析时借鉴灵敏度分析方法[23],首先将5个前提属性均作为分析属性,然后依照灵敏度分析中控制单一变量的方式,将评价等级A、 B上的置信度按等比例减少,并将减少的置信度转移至评价等级C上,因此可建立如下的等式:
 |
| 图 4 各置信规则库上的效用值和相似度的对比Fig. 4 Comparison of utility and similarity in belief rule bases |

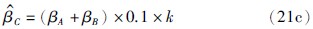
上式中灵敏度因子k=1,…,10,因此在分析时,可在灵敏度因子k的取值范围内依次增大灵敏度因子k的值,并依此比较BRB系统输出的平均效用值和相似度.
从平均效用值的角度分析,如图 5所示,由图 5(a)的6条曲线可知,随着灵敏度因子k值的增大,在6个置信规则库上的平均效用值呈现出两种变化趋势,其中O-BRB、 CCSD-BRB和D5-BRB呈现出指数变化的下降趋势,而其余3个置信规则库则呈现出近乎线性的变化趋势,虽然同为递减,但与O-BRB变化趋势的差异性较大,进一步比较CCSD-BRB与D5-BRB,由图中的曲线可知CCSD-BRB上的平均效用值更加接近O-BRB; 继续对各置信规则库上的平均效用值进行分析,由图 5(b)中各置信规则库的平均效用值的偏差均值可知,在CCSD-BRB上平均效用值的偏差均值最低,其次是D5-BRB,由此可见,在一般方案作为示例输入时CCSD约简方法能够确保BRB系统推理所得的平均效用值偏差最低.
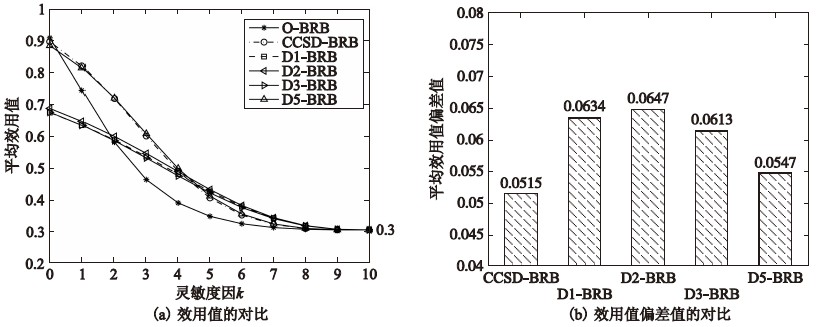 |
| 图 5 各置信规则库上的效用值和效用值偏差的对比Fig. 5 Comparison of utility and utility deviation in belief rule bases |
从相似度的角度分析,如图 6所示,由图 6(a)中6条曲线可知,随着灵敏度因子k值的增大,在6个置信规则库上相似度同样呈显出两种变化趋势,其中CCSD-BRB和D5-BRB在灵敏度因子k为2和3时偏离O-BRB较为明显,而对于其余的3个置信规则库在开始时偏离O-BRB较为明显,但5个置信规则库在灵敏度因子k大于6时均十分地接近O-BRB,因此由图 6(a)中的曲线很难判别CCSD约简方法对置信规则库的推理准确性的影响是否最小; 再继续对图 6(b)进行分析,其中图中的柱状图表示各置信规则库上的平均相似度,在图中仅有CCSD-BRB上平均相似度高于0.97,由此可见,在一般方案作为示例输入时CCSD约简方法能够保证BRB系统推理的相似度最高.
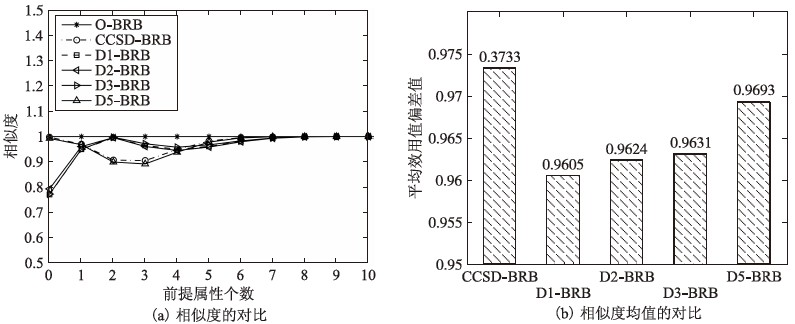 |
| 图 6 各置信规则库上的相似度和相似度均值的对比Fig. 6 Comparison of similarity and average similarity in belief rule bases |
综上所述,通过与约简关键属性后构建的置信规则库的对比可知,由CCSD约简方法约简所得的置信规则库具有较低效用偏差和较高相似度的特点,进而证明CCSD约简方法能够有效地确保BRB系统被约简后具有较高的准确性.
5 结论本文针对置信规则库中的“组合爆炸”问题及现有规则约简方法的不足提出基于关联系数标准差的规则约简方法,其利用计算属性权重的方式来实现维度约简的规则约简方法,通过约简关联权重相对较小的前提属性来完成精简置信规则库的目的. 此外,在以特殊方案和一般方案作为实验输入时,验证了本文所提出的规则约简方法在约简置信规则库后能够使其具有较低效用偏差和较高相似度的特点. 对于今后的研究,我们将进一步探索具有更理想约简效果的赋权方法,并将其应用于置信规则库的规则约简中.
| [1] | Yang J B,Liu J,Wang J,et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE Transactions on Systems,Man,and Cybernetics,Part A: Systems and Humans,2006,36(2): 266-285. |
| [2] | Dempster A P. A generalization of Bayesian inference[J]. Journal of the Royal Statistical Society,Series B: Methodological,1968,30(2): 205-247. |
| [3] | Shafer G. A mathematical theory of evidence[M]. Princeton,USA: Princeton University Press,1976. |
| [4] | Huang C L,Yong K. Multiple attribute decision making methods and applications: A state-of-art survey[M]. Berlin,Germany: Springer-Verlag,1981. |
| [5] | Zadeh L Z. Fuzzy sets[J]. Information and Control,1965,8(3): 338-353. |
| [6] | Sun R. Robust reasoning: Integration rule-based and similarity-based reasoning[J]. Artificial Intelligence,1995,75(2): 241-295. |
| [7] | Liu J,Yang J B,Ruan D,et al. Self-tuning of fuzzy belief rule bases for engineering system safety analysis[J]. Annals of Operations Research,2008,163(1): 143-168. |
| [8] | Yang J B,Liu J,Xu D L,et al. Optimizationmodel for training belief-rule-based systems[J]. IEEE Transactions on Systems,Man,and Cybernetics,Part A: Systems and Humans,2007,37(4): 569-585. |
| [9] | Zhou Z J,Hu C H,Yang J B,et al. Online updating belief-rule-based system for pipeline leak detection under expert intervention[J]. Expert Systems with Applications,2009,36(4): 7700-7709. |
| [10] | 姜江. 证据网络建模、推理及学习方法研究[D]. 长沙: 国防科技大学,2011. Jiang J. Modeling,reasoning and learning approach to evidential network[D]. Changsha: National University of Defense Technology,2011. |
| [11] | 周志杰. 置信规则库在线建模方法与故障预测[D]. 西安: 西安科技大学,2010. Zhou Z J. Online modeling methods of belief rule base and failure prognosis[D]. Xi'an: Xi'an University of Science and Technology,2010. |
| [12] | 周志杰,杨剑波,胡昌华,等. 置信规则库专家系统与复杂系统建模[M]. 北京: 科学出版社,2011. Zhou Z J,Yang J B,Hu C H,et al. Belief rule base expert system and complex system modeling[M]. Beijing: Science Press,2011. |
| [13] | Chang L L,Zhou Y,Jiang J,et al. Structure learning for belief rule base expert system: A comparative study[J]. Knowledge-Based Systems 2013,39(1): 159-172. |
| [14] | Roweis S T,Saul L K. Nonlinear dimensionality reduction by local linear embedding[J]. Science,2000,290(5500): 2323-2326. |
| [15] | Wang Y M,Luo Y. Integration of correlations with standard deviations for determining attribute weights in multiple attribute decision making[J]. Mathematical and Computer Modeling,2010,51(1): 1-12. |
| [16] | Yang J B,Xu D L. On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty[J]. IEEE Transactions on Systems,Man,and Cybenetics,Part A: Systems and Humans,2002,32(2): 289-304. |
| [17] | Wang Y M,Yang J B,Xu D L,et al. The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees[J]. European Journal of Operational Research,2006,175(1): 35-66. |
| [18] | Mcchrystal S A. Joint capabilities integration and development system[M]. Washington,USA: Chairman of the Joint Chiefs of Staff Instruction,2009. |
| [19] | 叶义成, 柯丽华, 黄德育. 系统综合评价技术及其应用[M]. 北京: 冶金工业出版社, 2006.Ye Y C, Ke L H, Huang D Y. System comprehensive evaluation technology and its application[M]. Beijing: Metallurgical Industry Press, 2006. |
| [20] | Pöyhönen M, Hämäläinen R P. On the convergence of multiattribute weighting methods[J]. Theory and Methodology, 2001, 129(3): 569-885. |
| [21] | 金菊良, 魏一鸣. 复杂系统广义智能评价方法与应用[M]. 北京: 科学出版社, 2008.Jin J L, Wei Y M. Generalized intelligent assessment methods for complex systems and applications[M]. Beijing: Science Press, 2008. |
| [22] | 舒康, 梁镇韩. AHP中的指数标度法[J]. 系统工程理论与实践, 1990, 10(1): 6-8.Shu K, Liang Z H. Exponential scaling method in AHP[J]. System Engineering Theory and Practice, 1990, 10(1): 6-8. |
| [23] | Yang J B, Xu D L. Nonlinear information aggregation via evidential reasoning in multiattribute decision analysis under uncertainty[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 2002, 32(3): 376-393. |



