文章快速检索  
  高级检索
引用本文
张桂涛, 胡劲松, 孙浩, 戴更新. 考虑产品寿命次数的多期闭环供应链网络均衡[J]. 信息与控制, 2015, 44(1): 29-37
ZHANG Guitao, HU Jinsong, SUN Hao, DAI Gengxin. The Closed-loop Supply Chain Network Equilibrium with Products Lifetime in Multi-period Planning Model[J]. INFORMATION AND CONTROL, 2015, 44(1): 29-37.
考虑产品寿命次数的多期闭环供应链网络均衡
张桂涛, 胡劲松, 孙浩, 戴更新    
青岛大学管理科学与工程系, 山东 青岛 266071
收稿日期: 2014-02-17; 录用日期: 2014-04-22; 修回日期: 2014-08-07
基金项目：国家自然科学基金资助项目（71202142，71371102）；国际（地区）合作与交流资助项目（71311120090）；山东省自然科学基金资助项目（ZR2012GM002）.
作者简介: 张桂涛（1975-），男，博士生，讲师. 研究领域为物流和供应链管理.
胡劲松（1966-），男，博士，教授，博士生导师. 研究领域为决策分析，物流与供应链管理.
孙 浩（1981-），男，博士，副教授. 研究领域为逆向物流与闭环供应链管理.
通讯作者：张桂涛,zhangguitao@qdu.edu.cn
摘要：在考虑产品寿命次数的基础上，研究了由多个制造商和多个消费市场组成的闭环供应链网络的多期动态均衡问题．采用变分不等式和互补理论获得了制造商和消费市场的最优性条件，进而建立了整个闭环供应链网络的均衡模型．采用定步长的修正投影收缩算法对模型进行求解，通过算例将不同寿命次数结合有关参数对网络均衡状态的影响进行了对比分析，给出了政府有关部门和供应链网络中制造商作决策时需关注的关键问题，本文所得结论为开展相关领域的研究提供一定的借鉴．
关键词： 闭环供应链网络     产品寿命次数     回收率     再制造    
The Closed-loop Supply Chain Network Equilibrium with Products Lifetime in Multi-period Planning Model
ZHANG Guitao , HU Jinsong, SUN Hao, DAI Gengxin     
School of Management Science and Engineering, Qingdao University, Qingdao 266071, China
Abstract:An equilibrium problem of multi-period dynamic closed-loop supply chain network,which comprises manufacturers and demand markets,based on the product's lifetime is studied. Using variational inequality and complementary theory,the optimal conditions for manufacturers and demand markets are formulated,and thus the integrated closed-loop supply chain network equilibrium model is established. The equilibrium is obtained by employing modified project contraction algorithm with fixed step. Using numerical examples,the impacts of different product lifetime and related parameters on the supply chain network equilibrium results are compared and analyzed,and the solution to a critical problem that is encountered while making decisions in the relevant departments of government and manufacturers in a supply chain network is provided. The results of this study can help promote research in other related fields.
closed-loop supply chain network     product lifetime     collection rate     remanufacturing    

1 引言

闭环供应链是近年来理论界和企业界关注的热点之一，它从产品全生命周期角度出发，将产品销售等正向物流活动和废旧品回收再制造等逆向物流活动纳入到供应链管理中，形成闭合回路结构[1]. 再制造是把消费者使用后的废旧品进行回收、 拆解和修复，并用于新产品生产的过程[2]. 鉴于再制造具有节能和对环境影响低等特点[3]，欧盟在2003年通过WEEE等立法形式促进企业对产品进行全生命周期管理，而我国2009年1月1日开始实施的《循环经济促进法》亦将再制造纳入法律范畴进行规范化处理[4]. 有关研究表明： 对核心部件的再制造能够节省大约40％～60％的成本[5]，许多国际知名企业，如Xerox、 Robert Bosch Tool、 Black and Decker和Hewlett-Packard等均通过再制造改善了自身收益[6, 7]. 但当前我国仍有许多企业对再制造能否带来利润存在疑虑，因此定量探讨再制造的经济性以及对制造商的回收再制造策略给予理论指导，对促进我国再制造产业的发展和企业闭环供应链管理水平的提高具有重要的意义.

对此学者们进行了大量研究[8, 9, 10, 11]，然而绝大多数文献都假定旧产品仅能再制造一次，事实上某些产品的核心组件可被再制造多次，如汽车外胎和计算机芯片可分别被再造3次和4次[12]. 基于此，Geyer[12]和李新军等[13]在考虑旧产品寿命次数的前提下，探讨了制造商实施再制造的经济性和生产优化问题. 以上两篇文献仅面向单一垄断制造商，未能纳入渠道竞争因素. 在当今日趋复杂的市场环境中，供应链整体表现为典型的层级网络结构，每层都具有众多类型相同且彼此竞争的渠道成员，如多个竞争的制造商及多个竞争的零售商等； 与此同时，异层间的成员又进行产品交易，体现出一定的合作性. 供应链网络在所有成员的竞争、 合作与交互过程中达到均衡状态. Nagurney等[14]首次分析了确定需求条件下的供应链网络均衡问题，是该领域的开篇之作，后续学者们分别将网络均衡模型推广至随机需求[15]、 模糊需求[16]和双渠道供应链网络[17]等情形. 在闭环供应链网络方面，Hammond和Beullens[18]研究了WEEE立法约束下的闭环供应链网络均衡问题； Yang等[19]研究了五级闭环供应链网络的静态均衡问题； 杨玉香等[20]建立了生产者责任延伸制度下由零售商回收的闭环供应链网络均衡模型； 张桂涛等[21]研究了含缺陷产品的双渠道闭环供应链网络均衡问题，但这些文献只考虑了单周期的最优决策. 近期少量学者探讨了多规划期下的动态供应链网络均衡问题. 张铁柱等[22]研究了存在双渠道交易的多期供应链网络均衡； Hamdouch等[23]从多规划期的角度并结合成员的购买策略，构建了具有能力约束的三层供应链网络均衡模型，但文[22, 23]仅针对传统正向供应链网络. 目前，多期动态环境下的闭环供应链网络均衡问题尚未见报道. 而在现实中，闭环供应链成员更多地要考虑多个规划期的盈利情况，如当制造商面临不同规划期间的原材料价格波动和市场需求变化时，其如何制定价格和回收再制造决策?此外，旧产品核心部件的可再制造次数对各成员各期的最优决策具有怎样的影响?在考虑上述实际因素的基础上，探讨闭环供应链网络的动态均衡条件无疑具有重要的理论价值和现实意义.

本文拟在考虑产品寿命次数的基础上，研究由制造商和消费市场组成的两级闭环供应链网络的多期动态均衡，通过分析相关参数变化对最优均衡解的影响，来阐明模型中蕴含的管理学启示.

2 模型假设与符号说明 2.1 模型假设

考虑由多个制造商和多个消费市场组成的闭环供应链网络，各制造商生产同质产品向各消费市场销售，并在每个规划期末从消费市场回收经消费者使用后产生的废旧品，用于下一期的再制造，其目标是使多规划期背景下的总利润最大化. 由2个制造商和2个消费市场组成的2期供应链网络可用图 1表示，其中M表示制造商，K表示消费市场，M21表示第2期的第1个制造商，其余符号可类似做出解释，不同规划期制造商间连接的虚线表示规划期之间的库存转移，制造商与消费市场间连接的实线表示正向的产品交易和逆向的废旧品回收.

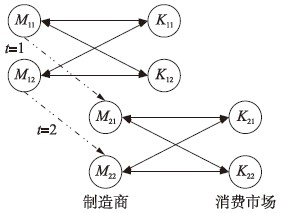图 1 由2制造商和2消费市场组成的2期闭环供应链网络Fig. 1 A closed-loop supply chain network consisting of two manufacturers and two demand markets with 2 periods
图选项

由于所研究问题的复杂性，本文做出如下假设：

假设1 每期销售的产品中，由于使用废旧品可以节约成本，因此优先采用回收品进行再制造.

假设2 再制造产品和采用原材料生产的产品无差异，在市场上以相同价格销售.

假设3 各制造商和消费市场在空间上是分离的，其地理位置体现在交易成本函数中.

假设4 模型中涉及的生产函数与交易成本函数均为连续可微凸函数.

假设5 规划期数大于产品寿命次数以体现产品寿命次数的影响.

2.2 变量和符号说明

T： 总规划期数；

Z： 产品的寿命次数，即产品可制造和再制造的总次数；

t： 某一个规划期，t=1，2，…，T；

m： 某一个制造商，m=1，2，…，M；

k： 某一个消费市场，k=1，2，…，K；

α： 回收率，政府要求的废旧品回收率，假设其在各期间不发生变化；

βr： 原材料转化率；

βui： 将回收的废旧品进行第i次再制造的转化率，i=1，…，min｛t-1，Z-1｝. 一般而言，旧产品核心组件的质量随再制造次数的增加而下降，因此假设βui≤βui-1，i=2，…，min｛t-1，Z-1｝；

qrm(t)： 制造商m于t期用于生产的原材料数量，所有制造商采用的原材料数量形成MT维列向量qr；

qmk(t)： 在t期从制造商m与消费市场k的产品交易量，所有的制造商与消费市场间的交易量形成MKT维列向量Q1；

qrmk(t)： qmk(t)中由原材料制造的产品数量，所有的qrmk(t)形成MKT维列向量Q2；

qukm(t)： 在t期从消费市场k到制造商m的废旧品交易量，所有消费市场到制造商间的交易量形成MKT维列向量Q3，且. 如Z=2，在第1期末回收的废旧品数量为αqrmk(1)，在第2期末回收的废旧品数量为αqrmk(2)+βu1α2qrmk(1)，以此类推在第3期末回收的废旧品数量为αqrmk(3)+βu1α2qrmk(2)；

qum(t)： 制造商m于t(t≥2)期用于再制造的废旧品数量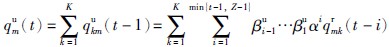，，所有制造商用于再制造的废旧品数量形成M(T-1)维列向量qu；

frm(qrm(t))： 在t期制造商m的原材料采购成本函数；

frm(t)=frm(βr，qrm(t))： 制造商m于t期用原材料生产时的生产成本函数；

fum(t)=fum(βui，qrmk(t-i))： 制造商m于t(t≥2)期采用废旧品再制造时的生产成本函数，i=1，…，min｛t-1，Z-1｝；

cukm(t)： 在t期，制造商m从消费市场k回收废旧品的运输成本函数；

cm(qum(t))： 制造商m于t(t≥2)期对数量为qum(t)的废旧品的处理成本函数；

Im(t)： 制造商m于t期的库存量，所有的Im(t)形成MT维列向量I；

Hm(t)=Hm(Im(t))： 制造商m于t期的库存成本函数；

ρmk(t)： 在t期，制造商m销售产品给消费市场k的产品交易价格，为内生变量；

ρ： 制造商对回收的废旧品处理过程中所产生废弃物的单位处理费用，为常数；

cmd(t)=cmd(βui，qrm(t))： 在t期，制造商m把处理废旧品产生的废弃物运送至掩埋地点的成本函数；

ρukm(t)： 在t期，消费市场k销售废旧品给制造商m的交易价格，为内生变量；

cmk(t)=cmk(qmk(t))： 在t期，消费市场k向制造商m购买产品时所承担的交易成本函数；

αk(Q3)： 消费者将废旧品卖给制造商的负效用函数；

ρDk(t)： 消费市场k于t期的单位产品需求价格，每期的ρDk(t)形成K维列向量ρDt，所有的ρDk(t)形成KT维列向量ρ；

dk(ρDt)： 消费市场k于t期的产品需求函数，为市场需求价格的单调减函数.

3 模型构建 3.1 制造商的最优行为及其均衡

制造商m于规划期t向消费市场销售产品，同时在期末从所有消费市场回收经消费者使用后的废旧品，以备在规划期t+1用于再制造. 第1个规划期制造商只使用原材料进行生产，第2期以后可以同时使用回收的废旧品和原材料进行生产. 由于考虑产品寿命次数Z，因此产品经过Z-1次再制造后，已不具有任何价值，需废弃处理. 根据前述假设，令βi=βuiβui-1…βu1，i=1，…，min｛t-1，Z-1｝. 各制造商间进行非合作竞争，且每个制造商均以实现其自身利润最大化为目标，制造商m的目标函数可表示如下：

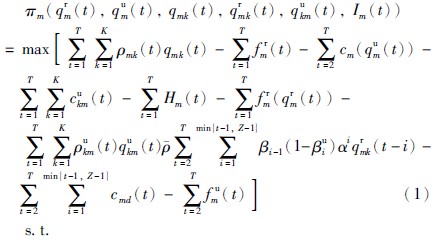
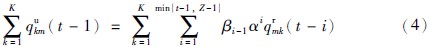
qrm(t)，qum(t)，qmk(t)，qrmk(t)，qukm(t)和Im(t)均大于等于0.

约束(2)表明当期的库存量加上销售给各消费市场的量，等于利用废旧品的再制造量、 利用原材料的生产量与上期转移到当期的库存量之和； 约束(3)表明制造商m从t-1期末回收的废旧品用于t期的再制造； 约束(4)表明制造商m在t-1期末从消费市场回收的废旧品数量为以前各期利用原材料生产并且还可以用于再制造的回收产品数量； 约束(5)说明销售给消费市场的产品中，包含新制造品和再制造品两部分. 所有制造商为实现其利润最大化目标，均在考虑其余制造商最优决策的条件下，决定其各期利用原材料最优数量qr*和Q3*、 各期再制造利用的废旧品数量qu*以及与各消费市场的产品交易量Q1*与废旧品的回收量Q2*、 各期转移到下一期的库存量I*. 因此，制造商层的最优性条件可以描述为变分不等式： 确定(qr*，qu*，Q1*，Q2*，Q3*，I*，γ*，η*，ϕ*，φ*)∈ΩM，满足

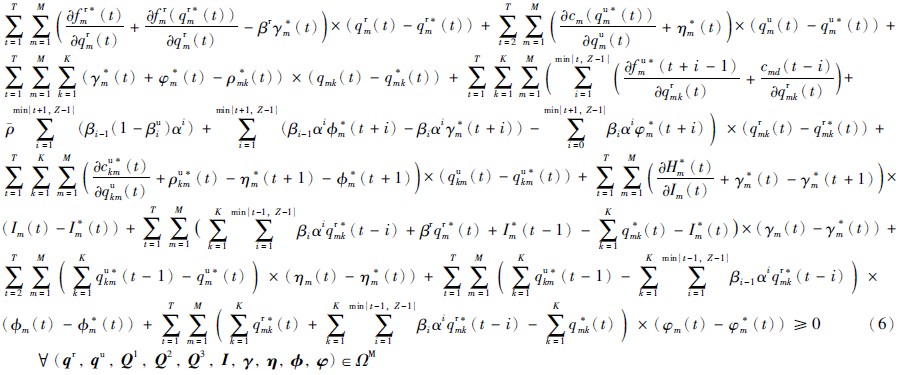
其中ΩM=｛(qr，qu，Q1，Q2，Q3，I，γ，η，ϕ，φ)∈RMT+M(T-1)+3MKT+MT+×R4MT｝.

式(6)中γm(t)、 ηm(t)、 ϕm(t)、 φm(t)分别为约束(2)、 (3)、 (4)和(5)对应的拉格朗日乘子，且γ、 η、 ϕ、 φ分别为拉格朗日乘子形成的MT维列向量.

由式(6)的第1项并根据变分不等式和互补关系间的等价关系可知，当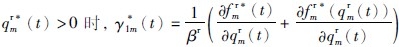，即制造商m于t期的原材料边际供应和边际生产成本的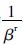倍； 根据第6项，制造商当期产品的边际库存成本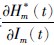加上当期边际供应和边际生产成本的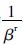倍，等于下一期边际供应成本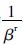倍的情况下，制造商才会决策保留当期库存到下一期销售，否则制造商不会考虑转移至下一期的库存.

3.2 消费市场的最优行为及其均衡

消费市场的决策变量有Q1、 Q3和ρ，即各个消费市场的消费者根据自身对产品的评价决定是否从各制造商处购买产品(包括购买的价格和数量)，以及是否在期末将使用后的废旧品卖给制造商.

根据文[16, 18, 19]，在产品销售过程中，在规划期t，消费市场k与所有制造商的交易满足互补条件

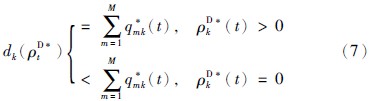
式(7)表明各制造商对消费市场k的供应量等于消费市场的需求量时，可以正常交易，即交易价格为正，否则交易不会发生，且各期需求量与每期所有消费市场的需求价格有关以体现各市场间的竞争.

由于消费市场的消费者要想获取产品，除了支付给制造商的购买费用外，还需支付为获取产品而必须的交通费用等，因此，类似于文[18, 19]，在规划期t，消费市场的需求价格和制造商的销售价格满足

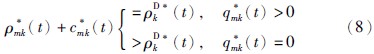
同样类似于文[18, 19]，在规划期t，消费市场中的消费者愿意把废旧品卖给制造商的偏好函数满足

且满足回收量约束

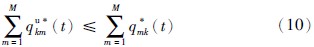
假设约束条件(10)对应的拉格朗日乘子为λk(t)，且所有λk(t)形成KT维列向量λ.

上述式(7)～(10)可以描述为变分不等式： 确定(Q1*，Q3*，ρ*，λ*)∈ΩK 满足

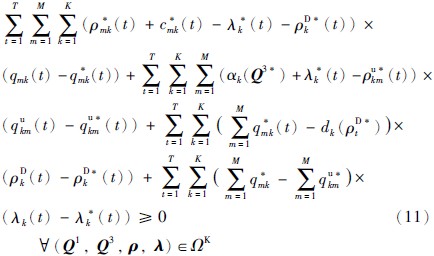
其中ΩK=｛(Q1，Q3，ρ，λ)∈R2MKT+2KT+｝.

式(11)的第2项表明，当存在逆向交易，即qu*km(t)>0时，ρu*km(t)=αk(Q3)+λ*k(t). 在实际应用中，式(11)最后1项的产品正向交易量和废旧品的逆向交易量，通常有qu*km(t) < q*mk(t)，即产品经消费后产生的废旧品总有部分不能回收，那么就有λ*k(t)=0，即ρu*km(t)=αk(Q3)，也就是说，逆向交易的价格是制造商支付给消费者用来补偿其由于废旧品回收产生的负效用.

3.3 多期闭环网络均衡模型

整个供应链网络的均衡是所有制造商各期采用原材料和废旧品生产的产品数量，与所有消费市场的交易量、 所有消费市场各期的需求量相一致； 消费市场的消费者于各期末愿意把部分废旧品经制造商回收并用于再制造的量与制造商愿意回收的量相一致，即整个供应链网络的均衡应同时满足式(6)和式(11)，把式(6)和式(11)相加，得到考虑产品寿命次数的多期闭环供应链网络均衡的条件为： 确定(qr*，qu*，Q1*，Q2*，Q3*，I*，ρ*，γ*，η*，ϕ*，φ*，λ*)∈Ω，满足

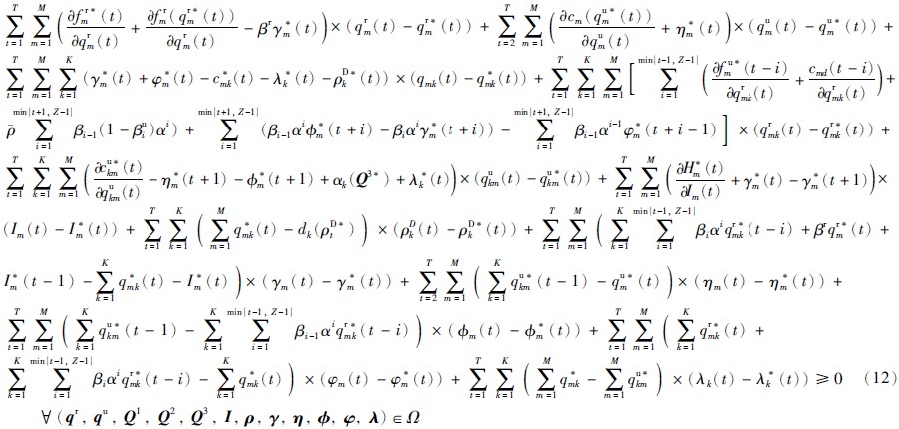
其中，Ω=ΩM×ΩK.

4 算例分析

以2个制造商和2个消费市场组成的供应链网络作算例分析，并考虑产品可再制造次数为1次和2次，即Z=2和Z=3，总的规划期数T=5. 引入变量δ，当δ=0时，表示是Z=2的情形； 当δ=1时，表示是Z=3的情形. 当δ=0时，在第1期采用原材料生产，第2期后利用回收的废旧品和原材料进行生产，从第3期开始有部分废旧品超出寿命次数而不再回收； 当δ=1时，在第1期采用原材料生产，第2期和第3期同时采用回收的废旧品和原材料进行生产，第4期开始以及到第5期有部分废旧品因超出产品寿命次数而不再回收. 涉及的各成本函数和交易函数如下.

制造商层第1期至第5期的原材料采购成本函数：

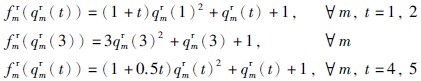
制造商层第1期至第5期采用原材料生产的生产成本函数：

制造商层第2期至第5期采用废旧品再制造的生产成本函数：

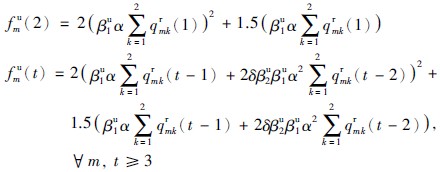
制造商的库存成本函数：

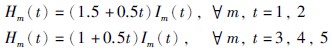
制造商对回收的废旧产品进行处理的成本函数：

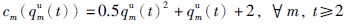
制造商回收废旧品的运送成本函数：

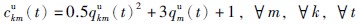
制造商把回收的废旧品经处理后的废弃部分进行掩埋处理的运输费用：

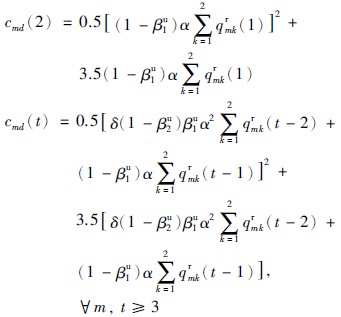
消费市场承担的与制造商间的交易费用函数：

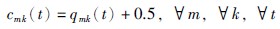
消费者对废旧品卖给制造商的负效用函数：

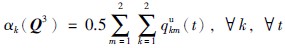
消费市场的需求函数：

求解变分不等式的算法主要有修正投影算法[23]与对数二次型预测与校正算法[24]等，这里利用修正投影算法对模型求解，迭代步长为0.01，终止条件为10-8，利用Matlab编程. 算例主要分析以下三个方面： (1) 通常原材料的转化率高于回收品的再制造转化率，因而不妨将βr设置为较大的值，即令βr=1或βr=0.95； 此外，第二次再制造转化率βu2一般不高于第一次再制造转化率βu1，因此选取0.95≥βu1≥βu2≥0.5，在此基础上考察第一次和第二次再制造转化率对制造商利润的影响，结果如图 2所示； (2) 遵循上述原则，选取βr=1，βu1=0.9，βu2=0.6，=1，分别针对δ=0和δ=1的两种情况，分析回收率α的变化对供应链网络均衡的影响，结果如表 1和表 2所示； (3) 同样遵循以上原则，选取βr=1，βu1=0.9，βu2=0.6，α=0.3，分别针对δ=0和δ=1，分析废弃物掩埋等单位处理费用对供应链网络均衡的影响，结果如表 3所示.

图 2中的交叉点处为制造商在相应两次再制造转化率处对应的利润. 从图 2(a)和图 2(b)可以看出，在本算例中，第一次再制造转化率和第二次再制造转化率对制造商的利润均有影响并基本呈现线性关系，但重要性显然不同. 由于第一次回收和用于再制造的废旧品数量较多，故第一次再制造转化率对制造商的利润影响较大； 废旧品经过第一次回收和再制造后，第二次可再利用的数量已经比较有限，因此第二次再制造转化率对制造商影响较小. 把图 2(a)和图 2(b)的对应点进行对比发现，相对于两次再制造转化率，制造商的利润受原材料转化率βr的影响更大，如在点βu1=βu2=0.95，制造商利润在βr=1时比βr=0.95时高约6.83； 在点βu1=βu2=0.5，制造商利润在βr=1时比βr=0.95时高约5.84，而βu1每增加0.05，制造商利润约增加3.5，βu2每增加0.05，制造商利润约增加0.5，即βr、 βu1和βu2对制造商利润影响大小的顺序为： βr>βu1>βu2.

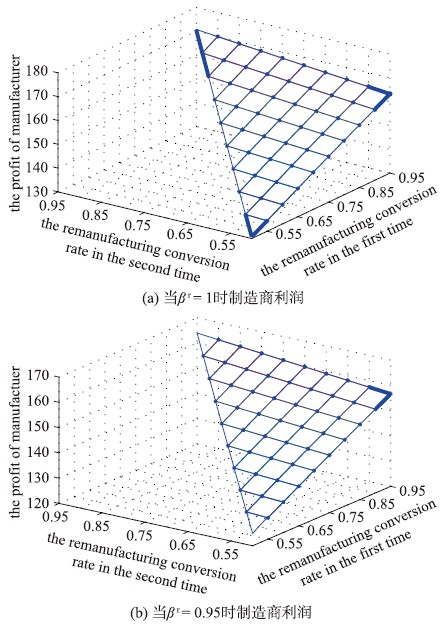图 2 两次再制造转化率对制造商利润的影响Fig. 2 The impact of two remanufacturing conversion rate on the manufacturers′ profits
图选项

表 1中各行表示各期的变量值，qum从第2期开始，所以只有4行. 从表 1可以看出，消费市场需求和制造商利润均随回收率α的增加而增加，但增加幅度却逐渐变小，主要原因在于随着回收量的增加，消费者将废旧品卖给制造商的意愿会逐步降低，换言之，制造商的回收难度及其为回收废旧品支付的边际费用会逐步提高. 因此，可以推断，当回收比例增加到某临界值时，制造商的利润将达到最大，此后α增加会使制造商的利润减少，即呈现出收益递减规律. 此外，在表 1中，随着α的增加，回收的废旧品数量一直稳步增加，总的原材料使用量和前4期的原材料使用量均先增加后减少，即α的增加虽提高了可再利用的废旧品数量，却并没有简单地减少原材料使用量，主要原因是回收量稳步增加的同时刺激了市场需求，导致当α达到某临界值之前，原材料的需求量也增加(本例中其在α=0.4附近达到最大值)，在此之后由于回收和可再制造的废旧品数量已足够多，从而使原材料使用量减少，整个供应链网络以及制造商的利润随回收率的增加而提升. 对于第5期，因是规划期的最后一期，其趋势与前几期有所不同，原材料使用量由于回收量持续增加而呈现一直减少的趋势.

表 1 δ=0时，α变化对供应链网络均衡状态的影响 Tab. 1 When δ=0，the impact of α on the supply chain network equilibrium results
α0.10.20.30.40.5

qr*m
2.779 6
2.251 4
2.193 6
2.543 0
2.098 3
2.918 1
2.355 2
2.289 5
2.646 9
2.081 0
3.001 5
2.417 8
2.347 2
2.709 5
2.063 7
3.033 1
2.441 5
2.369 1
2.733 1
2.047 3
3.019 6
2.431 4
2.359 7
2.723 0
2.032 4
qu*m
0.227 0
0.190 2
0.258 0
0.301 6
0.453 4
0.399 3
0.538 0
0.651 2
0.680 8
0.633 4
0.825 9
1.002 7
0.905 8
0.878 6
1.112 4
1.333 9
1.121 9
1.120 2
1.387 9
1.636 9
qr*mk
1.135 1
0.950 8
1.290 2
1.507 8
1.049 2
1.133 5
0.998 3
1.345 0
1.628 0
1.040 5
1.134 6
1.055 6
1.376 5
1.671 2
1.031 8
1.132 3
1.098 3
1.390 5
1.667 3
1.023 7
1.121 9
1.120 2
1.387 9
1.636 9
1.016 2
q*mk
1.135 1
1.052 9
1.375 7
1.623 9
1.184 9
1.133 5
1.202 3
1.524 7
1.870 1
1.333 6
1.134 6
1.362 0
1.661 6
2.042 8
1.483 1
1.132 3
1.505 9
1.785 9
2.167 9
1.623 9
1.121 9
1.625 0
1.892 0
2.261 5
1.752 8
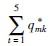6.372 57.064 27.684 18.215 98.653 2
I*m
0.509 5
0.859 3
0.472 5
0
0
0.651 0
1.009 7
0.609 0
0
0
0.732 3
1.038 8
0.632 9
0
0
0.768 5
1.013 4
0.601 5
0
0
0.775 9
0.966 9
0.550 8
0
0
πm134.166 3148.235 2160.414 7170.461 9178.357 9
表选项

表 2中数据的总体变化趋势与表 1大致相同，即网络的总交易量和各制造商的利润呈增加趋势，原材料使用量呈先增加后减少的趋势. 将两张表格横向比较可知： 当政府规定的回收率α≤0.3时，表 2中的制造商利润高于表 1，反之当α>0.3时，表 2中的制造商利润低于表 1. 该结论表明： 当政府制定的回收率适中时，产品寿命次数的增加对制造商是有利的； 反之当政府要求的回收率过高时，由于产品寿命次数增加为制造商带来的成本节约已不能弥补因回收次数增加所导致的回收成本增加，因而制造商利润不升反降. 该结论表明： 政府在制定政策时不能简单地追求高回收率，而应以企业实施逆向物流的实际情况为依据，充分了解其回收成本结构和再制造成本结构，然后在此基础上确定合理的回收比例，只有这样才能兼顾环境保护和企业经济效益的双重目标.

表 2 δ=1时，α变化对供应链网络均衡状态的影响 Tab. 2 When δ=1，the impact of α on the supply chain network equilibrium results
α0.10.20.30.40.5

qr*m
2.753 7
2.231 9
2.175 6
2.523 6
2.085 5
2.839 7
2.296 5
2.235 2
2.588 1
2.073 4
2.848 2
2.302 8
2.241 0
2.594 5
2.048 7
2.776 8
2.249 2
2.191 6
2.540 9
2.024 4
2.642 7
2.148 7
2.098 8
2.440 3
2.002 1
qu*m
0.214 9
0.194 3
0.250 4
0.345 1
0.442 7
0.449 7
0.491 3
0.830 9
0.659 9
0.782 0
0.682 4
1.353 0
0.842 2
1.166 1
0.837 5
1.861 1
0.977 6
1.553 1
0.964 0
2.319 8
qr*mk
1.074 7
0.874 7
1.173 4
1.619 8
1.142 6
1.106 8
0.925 1
1.061 6
1.886 2
1.036 7
1.099 9
1.006 4
0.865 7
2.021 2
1.024 4
1.052 7
1.078 7
0.658 5
2.089 3
1.012 2
0.977 6
1.113 1
0.463 0
2.111 4
1.001 1
q*mk
1.074 7
0.971 4
1.258 0
1.730 1
1.294 7
1.106 8
1.124 4
1.252 1
2.097 3
1.399 2
1.099 9
1.303 4
1.190 9
2.303 9
1.612 2
1.052 7
1.457 7
1.137 8
2.419 6
1.821 3
0.977 6
1.553 1
1.095 9
2.470 1
2.013 7
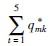6.328 96.979 87.510 37.889 18.110 4
I*m
0.604 3
1.086 8
0.915 6
0.199 7
0
0.626 2
1.072 3
1.184 3
0
0
0.648 4
0.938 3
1.448 0
0
0
0.671 4
0.763 2
1.637 8
0
0
0.687 4
0.609 8
1.782 5
0
0
πm134.689 8149.476 2161.382 5169.152 0172.442 2
表选项

表 3给出了制造商废弃处理成本的变化对两种产品寿命次数情形下网络均衡解及制造商利润的影响. 在此，废弃物处理成本可理解为政府向企业征收的税费与废旧品的处理成本的总和. 观察表 3可知： 无论δ=0或δ=1，的增加会导致制造商的原材料使用量、 废旧品回收量、 网络中的产品交易量以及制造商利润的降低； 当≤5时，δ=1情形下的制造商利润较优，而当增至10时δ=0情形下的制造商利润较优. 该结论表明： 政府征税在一定程度上抑制了闭环供应链网络中的经济活动； 此外，产品寿命次数越大，税费提高对企业收益的影响越大，其原因是在高税费情形下，寿命次数的增加会大大加重企业回收和废弃物处理的负担.

5 结论

本文针对由制造商和消费市场组成的多期闭环供应链网络，在考虑产品寿命次数的前提下，用变分不等式和均衡理论建立了整个供应链网络的均衡模型，利用修正投影收缩算法进行求解. 分别通过产品寿命次数为2次和3次，总规划期为5期的算例验证了所建模型，对模型中主要参数的变化对供应链网络均衡的影响进行了比较静态分析，得到了一定的管理学启示，主要结论如下：

表 3 对供应链网络均衡状态的影响 Tab. 3 The impact of on the supply chain network equilibrium results
均衡状态δ=0δ=1
ρ=1ρ=5ρ=10ρ=1ρ=5ρ=10
qr*m
3.001 5
2.417 8
2.347 2
2.709 5
2.063 7
2.990 2
2.409 3
2.339 3
2.701 0
2.063 8
2.976 0
2.398 7
2.329 5
2.690 3
2.064 0
2.848 2
2.302 8
2.241 0
2.594 5
2.048 7
2.829 3
2.288 6
2.228 0
2.580 3
2.048 2
2.805 7
2.270 9
2.211 6
2.562 6
2.047 5
qu*m
0.680 8
0.633 4
0.825 9
1.002 7
0.677 9
0.630 9
0.823 4
0.999 8
0.674 4
0.627 7
0.820 1
0.996 1
0.659 9
0.782 0
0.682 4
1.353 0
0.648 6
0.777 1
0.662 6
1.362 3
0.634 3
0.770 9
0.637 7
1.373 9
qr*mk
1.134 6
1.055 6
1.376 5
1.671 2
1.031 8
1.129 9
1.051 4
1.372 3
1.666 3
1.031 9
1.124 0
1.046 2
1.366 9
1.660 1
1.032 0
1.099 9
1.006 4
0.865 7
2.021 2
1.024 4
1.080 9
1.003 3
0.833 4
2.045 5
1.024 1
1.057 2
0.999 4
0.793 0
2.075 8
1.023 7
q*mk
1.134 6
1.362 0
1.661 6
2.042 8
1.483 1
1.129 9
1.356 5
1.656 1
2.036 8
1.481 8
1.124 0
1.349 7
1.649 4
2.029 2
1.480 3
1.099 9
1.303 4
1.190 9
2.303 9
1.612 2
1.080 9
1.295 2
1.156 8
2.319 2
1.616 9
1.057 2
1.284 9
1.114 2
2.338 4
1.622 7
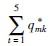7.684 17.661 17.632 67.510 37.469 07.417 4
πm160.414 7159.374 5158.079 3161.382 5159.429 5157.007 1
表选项

(1) 原材料转化率对网络运作以及制造商收益的影响大于再制造转化率，且再制造次数越多，其转化率影响越小.

(2) 当政府要求的回收率适中时，产品寿命次数的增加会刺激闭环供应链网络中的经济活动，提高废旧品回收率和制造商利润； 相反当回收率目标过高时，产品寿命次数的增加会加重制造商的负担，效果适得其反. 因而政府应根据制造商的回收成本结构以及再制造成本结构制定合理的回收率，从而兼顾环保目标与企业经济目标.

(3) 政府对于制造商废弃物处理税费的征收会抑制闭环供应链网络中的经济活动，高税费对多寿命次数情形下的网络运作绩效和企业收益影响更加显著. 建议除采取征税措施外，政府还应对制造商的回收再制造行为实施经济上的扶持.

本文的研究存在一定的不足，如假设闭环供应链网络中仅包含制造商和消费者两类渠道成员，并只考虑了市场需求确定的情形，未来可探讨市场需求随机且包含更多渠道成员参与的动态供应链网络均衡问题.

参考文献
[1] Margarete A S,Ken P. Meeting the closed-loop challenge: The case of remanufacturing[J]. California Management Review,2004,46(2): 74-89.
[2] Ferrer G,Swaminathan J M. Managing new and differentiated remanufactured products[J]. European Journal of Operational Research,2010,203(2): 370-379.
[3] Chen J M,Chang C I. The competitive strategy of a closed-loop supply chain with remanufacturing[J]. Transportation Research: Part E,2012,48(2): 387-400.
[4] 郭军华,李帮义,倪明. WTP差异下的再制造进入决策研究[J]. 中国管理科学,2013,21(1): 149-156. Guo J H,Li B Y,Ni M. Research on remanufacturing entry decision based on WTP differentiation[J]. Chinese Journal of Management Science,2013,21(1): 149-156.
[5] Giuntini R,Gaudette K. Remanufacturing: The next great opportunity for boosting US productivity[J]. Business Horizons,2003,46(6): 41-48.
[6] Atasu A,Jr Guide V D R,Van Wassenhove L N. So what if remanufacturing cannibalizes my new product sales?[J]. California Management Review,2010,52(2): 56-76.
[7] Martin P,Jr Guide V D R,Craighead C W. Supply chain sourcing remanufacturing operations: An empirical investigation of remake versus buy[J]. Decision Sciences,2010,41(2): 301-324.
[8] Savaskan R C,Bhattacharya S,Van Wassenhove L N. Closed-loop supply chain models with product remanufacturing[J]. Management Science,2004,50(2): 239-252.
[9] Debo L G,Toktay L B,Van Wassenhove L N. Market segmentation and product technology selection for remanufacturable products[J]. Management Science,2005,51(8): 1193-1205.
[10] 孙浩,达庆利. 基于产品差异的再制造闭环供应链定价与协调研究[J]. 管理学报,2010,7(5): 733-738. Sun H,Da Q L. Pricing and coordination of remanufacturing closed-loop supply chain based on product differentiation[J]. Chinese Journal of Management,2010,7(5): 733-738.
[11] 熊中楷,王凯,熊榆,等. 考虑经销商从事再制造的闭环供应链模式[J]. 系统工程学报,2011,26(6): 792-799. Xiong Z K,Wang K,Xiong Y,et al. Closed-loop supply chain considering that the distributor engages in remanufacturing[J]. Journal of Systems Engineering,2011,26(6): 792-799.
[12] Geyer R. The economics of remanufacturing under limited component durability and finite product life cycles[J]. Management Science,2007,53(1): 88-100.
[13] 李新军,达庆利. 基于产品寿命次数的闭环供应链生态优化问题研究[J]. 管理工程学报,2009,23(2): 50-54. Li X J,Da Q L. Monopoly production optimization problem for product lifetime in closed-loop supply chains[J]. Journal of Industrial Engineering and Engineering Management,2009,23(2): 50-54.
[14] Nagurney A,Dong J,Zhang D. A supply chain network equilibrium model[J]. Transportation Research: Part E,2002,38(5): 281-303.
[15] Dong J,Zhang D,Nagurney A. A supply chain network equilibrium model with random demands[J]. European Journal of Operational Research,2004,156(1): 194-212.
[16] 胡劲松,徐元吉,刘芳霞,等. 具有模糊需求的多商品流供应链网络均衡研究[J]. 控制与决策,2012,27(5): 665-672. Hu J S,Xu Y J,Liu F X,et al. A multi-products flow supply chain network equilibrium with fuzzy demand[J]. Control and Decision,2012,27(5): 665-672.
[17] Nagurney A,Cruz J,Dong J,et al. Supply chain networks,electronic commerce,and supply side and demand side risk[J]. European Journal of Operational Research,2005,164(1): 120-142.
[18] Hammond D,Beullens P. Closed-loop supply chain network equilibrium under legislation[J]. European Journal of Operational Research,2007,183(2): 895-908.
[19] Yang G F,Wang Z P,Li X Q. The optimization of the closed-loop supply chain network[J]. Transportation Research: Part E,2009,45(1): 16-28.
[20] 杨玉香,周根贵. EPR下供应链网络报废产品排放内生污染税模型[J]. 管理科学学报,2011,14(10): 67-76. Yang Y X,Zhou G G. An endogenous EOL products emission taxes model for supply chain network under EPR[J]. Journal of Management Sciences in China,2011,14(10): 67-76.
[21] 张桂涛,胡劲松,孙浩,等. 具有缺陷产品的双渠道闭环供应链网络均衡[J]. 中国管理科学,2013,21(5): 68-79. Zhang G T,Hu J S,Sun H,et al. The equilibrium of closed-loop supply chain network with dual channel and imperfect product [J]. Chinese Journal of Management Science,2013,21(5): 68-79.
[22] 张铁柱,周倩. 双渠道多期供应链网络均衡模型研究[J]. 计算机集成制造系统,2008,14(8): 1512-1520. Zhang T Z,Zhou Q. Multi-period supply chain network equilibrium model with two-channel[J]. Computer Integrated Manufacturing Systems,2008,14(8): 1512-1520.
[23] Hamdouch Y. Multi-period supply chain network equilibrium with capacity constraints and purchasing strategies[J]. Transportation Research: Part C,2011,19(5): 803-820.
[24] Korpelevich G M. The extra gradient method for finding saddle points and other problems[J]. Matekon,1977,13(1): 35-49.
[25] He B S,Xu Y,Yuan X M. A logarithmic-quadratic proximal prediction-correction method for structured monotone variational inequalities[J]. Computational Optimization and Applications,2006,35(1): 19-46.
"http://dx.doi.org/10.13976/j.cnki.xk.2015.0029"
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

张桂涛, 胡劲松, 孙浩, 戴更新
ZHANG Guitao, HU Jinsong, SUN Hao, DAI Gengxin
考虑产品寿命次数的多期闭环供应链网络均衡
The Closed-loop Supply Chain Network Equilibrium with Products Lifetime in Multi-period Planning Model
信息与控制, 2015, 44(1): 29-37.
INFORMATION AND CONTROL, 2015, 44(1): 29-37.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0029

文章历史

收稿日期：2014-02-17
录用日期：2014-04-22
修回日期：2014-08-07

工作空间