文章快速检索  
  高级检索
引用本文
李先宏, 于海斌, 曾鹏, 苑明哲, 孙兰香. 低阶被控过程含延迟的饱和最优PID控制器设计方法[J]. 信息与控制, 2015, 44(1): 43-50
LI Xianhong, YU Haibin, ZENG Peng, YUAN Mingzhe, SUN Lanxiang. A Design Method of Saturated Optimal PID Controller for the Low-order Controlled Processes with Time Delay[J]. INFORMATION AND CONTROL, 2015, 44(1): 43-50.
低阶被控过程含延迟的饱和最优PID控制器设计方法
李先宏, 于海斌, 曾鹏, 苑明哲, 孙兰香    
中国科学院沈阳自动化研究所工业控制网络与系统研究室, 辽宁 沈阳 110016
收稿日期: 2014-06-23; 录用日期: 2014-08-25; 修回日期: 2014-09-10
基金项目：中国科学院重要方向资助项目（KGCX2-EW-104）.
作者简介: 李先宏（1983-），男，博士，助理研究员. 研究领域为工业自动化与控制，智能电网系统建模、分析及优化方法等.
于海斌（1964-），男，博士，研究员. 研究领域为工业自动化，无线通讯，智能电网系统等.
曾 鹏（1976-），男，博士，研究员. 研究领域为工业通讯，智能电网系统，CPS物理网络系统等.
通讯作者：于海斌，yhb@sia.cn
摘要：实际控制器的输出信号是有界信号，即控制器输出饱和问题．针对控制器输出饱和问题，本文提出了低阶被控过程含延迟的一种饱和最优PID控制器设计方法．将控制误差及1阶、2阶、3阶微分项，及它们的混合项作为优化性能指标，建立了含有状态约束、稳定性及代数约束的非线性最优控制问题．应用共同李亚普诺夫函数定理与李亚普诺夫定理，约束最优控制问题被转化为非线性约束最优化问题，通过求解相应的非线性约束最优化问题，可获得饱和最优PID控制器参数．仿真结果表明了设计方法的可行性和有效性．
关键词： 控制器输出饱和问题     饱和最优PID（proportional integral derivative）控制器     约束最优控制问题     非线性约束最优化问题    
A Design Method of Saturated Optimal PID Controller for the Low-order Controlled Processes with Time Delay
LI Xianhong, YU Haibin , ZENG Peng, YUAN Mingzhe, SUN Lanxiang     
Key Laboratory of Industrial Control Network and Systems, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China
Abstract:In actual control systems,the controller's output signal is bounded,which is the controller's output saturated problem. This paper presents a design method of saturated optimal proportional integral derivative (PID) controller for low-order processes with time delay. The controller error,first-order error derivative,second-order error derivative,third-order error derivative,and their cross-items are used to calculate performance index. Subsequently,a nonlinear optimal control problem with the state constraint,and stability and algebraic constraint is proposed. The constraint optimal control problem is transformed into the nonlinear constraint optimization problem using common Lyapunov functions and Lyapunov theorems. Thus,the saturated optimal PID controller can be obtained by solving the nonlinear constraint optimization problem. The simulation results illustrate effectiveness and usefulness of the proposed design method.
controller's output saturation problem     saturated optimal PID(proportional integral derivative) controller     constraint optimal control problem     nonlinear constraint optimization problem    

1 引言

PID控制器被广泛应用于各种工业控制系统，它大约占到90％左右，PID控制器结构简单，物理意义明显，参数调整方便，因此深受广大工程技术人员的喜爱[1]. 随着控制理论与技术的不断发展，许多学者和研究人员对PID控制器的分析与设计进行了深入研究.

文[1]分析、 提出、 总结了PID控制器的设计方法，给出PID控制器在时域、 频域的设计步骤及性能评价指标等. 文[2, 3]最早提出了经典的Ziegler-Nichols(Z-N)和Cohen-Coon(C-C) PID控制器调节方法，通过应用继电器产生周期性振荡来整定控制器. 基于描述函数方法，文[4]提出了含有死区饱和的非线性系统PID控制器设计方法. 文[5]提出了混合H2/H∞性能的鲁棒最优PID控制器设计方法. 文[6]提出了基于双线性不等式优化的多变量最优PID控制器设计方法. 基于忆阻神经网络，文[7]提出了一种PID控制器设计方法. 文[8]采用标准线性矩阵不等式方法设计多变量H∞鲁棒最优PID控制器. 文[9]采用多目标优化绝对误差积分性能指标，获得低阶被控过程最优PID控制器. 基于参数最优化方法、 新区间多项式稳定准则，文[10, 11, 12, 13, 14, 15]提出了最小方差PID控制器、 鲁棒最优PID控制器及带动态性能约束与ε-Routh稳定性约束的最优PID控制器.

文[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]提出的PID控制器及最优PID控制器设计方法多数都不考虑控制器输出饱和问题. 实际控制器输出信号都是有界信号，在设计控制器时考虑控制信号饱和更符合实际情况. 引入饱和特性，对于最优PID控制器设计最直接的影响是： 控制系统变成了非线性系统，线性最优控制问题变成了非线性最优控制问题.

如图 1所示的饱和最优PID控制器闭环反馈系统，本文提出的饱和最优PID控制器设计方法，主要针对延迟时的低阶被控过程展开研究. 工业生产过程包含大量的简单环节，这些简单环节不可缺少，而这些简单环节多数可用低阶传递函数加延迟环节来描述.

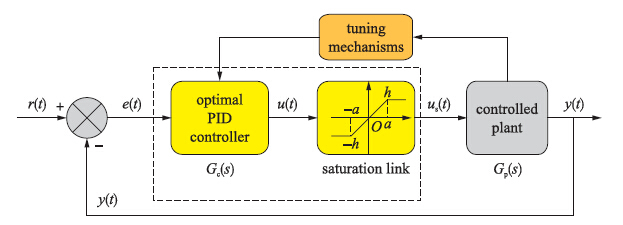图 1 带有饱和最优PID控制器的闭环反馈系统Fig. 1 Closed-loop feedback system with saturated optimal PID controller
图选项
2 饱和最优控制问题描述

PID控制器被广泛应用于工业控制领域，多数PID控制器调节方法不考虑控制器饱和特性. 控制器输出饱和表明了实际控制系统的固有特点，反映了控制系统的非线性特性及控制器调节范围. 如图 1含有饱和环节的闭环反馈系统，本文研究饱和最优PID控制器使得闭环系统具有某种最佳性能. 针对含延时的低阶过程，本文的非线性最优控制问题可描述为： 1) 饱和最优控制器能使闭环控制系统保持渐近稳定； 2) 饱和最优控制器能使性能指标实现极小化.

本文提出的非线性最优控制器设计问题包含控制系统的稳定性约束，状态及代数约束等. 设计饱和最优PID控制器时，需应用下述定理，定理内容如下：

共同李亚普诺夫函数定理[16, 17, 18]： 对于线性切换系统Π，对于任意的切换信号σ，线性切换系统Π保持渐近稳定的充分必要条件是： 系统Π的所有子系统都具有共同李亚普诺夫函数，即所有子系统满足下列关系：

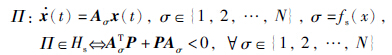
其中，Hs代表渐近稳定的线性切换系统集合，N是线性切换系统的子系统个数. 对于切换系统而言，共同李亚普诺夫函数定理也被称为单李亚普诺夫函数定理.

李亚普诺夫定理1[19, 20] 线性时不变系统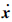=Ax保持渐近稳定的充分必要条件是： 对于任意给定的矩阵Q=QT≥0，存在一个矩阵P=PT≥0满足代数李亚普诺夫方程： ATP+PA=-Q.

李亚普诺夫定理2[19, 20] 对于线性时不变系统=Ax，x(0)=x0保持渐近稳定，任意给定矩阵Q=QT≥0，那么对于性能指标J将会有下列等价关系：

3 低阶被控过程含延时的饱和最优PID控制器设计步骤

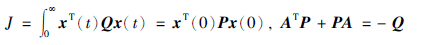
如图 1所示的闭环反馈系统，针对含有延时的低阶被控过程，本文提出了饱和最优PID控制器设计方法. 为了不失一般性，假设含延时的低阶被控过程Gp(s)可用如下传递函数来描述：

其中a0，a1，a2，b1，b2是系统参数，那么闭环反馈控制系统可用如下方程来描述：

其中，k是饱和斜率，α是饱和角，a是PID控制器饱和阈值，h是控制器的饱和输出，kp、 ki、 kd是PID控制器参数，e(t)是控制误差，u(t)是控制器输出，us(t)是控制器实际输出，r(t)是指令信号，y(s)是控制系统输出，Gc(s)是PID控制器. 首先考虑两种情况，即PID控制器输出饱和时，那么很显然闭环系统可用下述方程描述：

case 1：

case 2：

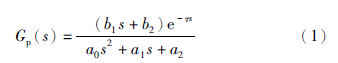
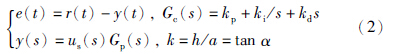
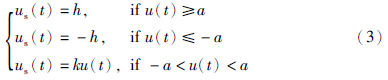
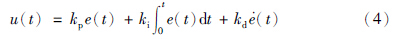
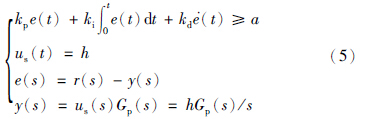
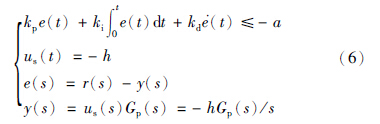
方程(5)、 (6)进一步写为下述等价形式：

case 1：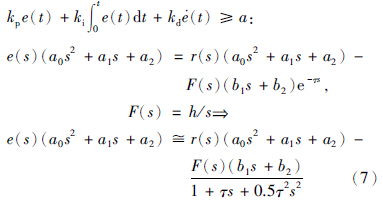

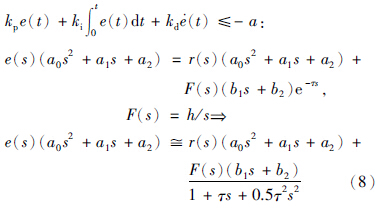
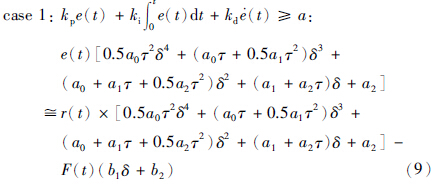
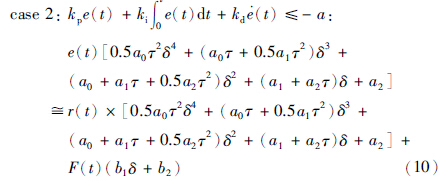
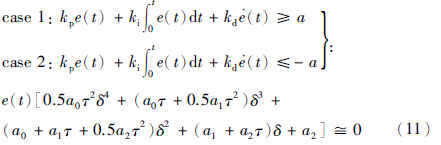
case 2：

其中在case 1与case 2情况下，将延迟环节e-τs采用2阶泰勒近似，得到有理分式的闭环误差方程. 然后对方程(7)、 (8)取逆拉普拉斯变换，得到相应的误差微分方程：

其中δ是微分算子，当指令信号r(t)为常值信号、 时间多项式、 甚至分段常值信号，case 1与case 2分别满足关系a2r(t)=±b2F(t)时，case 1与case 2误差微分方程共同表示为

获得case 1与case 2情况下的误差状态空间方程：

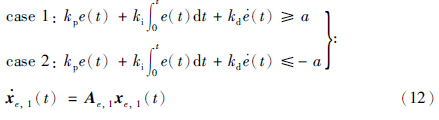
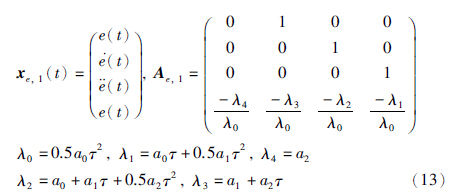
同理，当控制器实际输出在饱和阈值范围内时，闭环反馈系统可用下述方程描述：

case 3：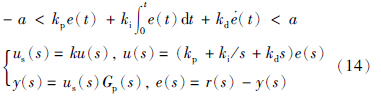

那么得到case 3情况下的闭环误差方程：

case 3：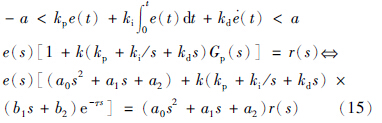

在case 3情况下，将延迟环节采用1阶近似，e-τs采用泰勒1阶近似展开，闭环误差方程可写成下述形式：

case 3：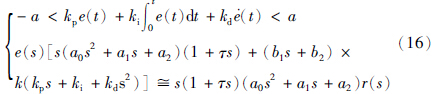

当指令信号r(t)为常值信号、 时间多项式信号、 甚至分段常值信号时，对方程(16)取逆拉普拉斯变换，得到相应的误差微分方程：

case 3：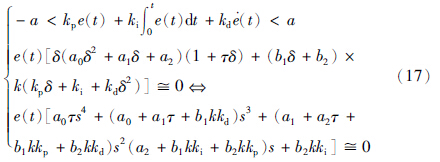

那么得到case 3情况下的误差状态空间方程：

case 3：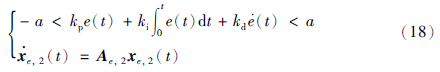

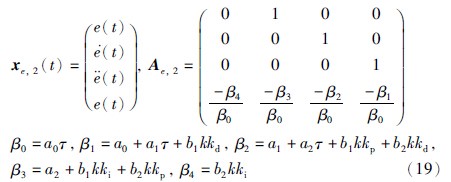
其中状态变量xe，2及状态矩阵Ae，2及其系统参数为

状态变量xe，1=xe，2，误差状态空间方程最终写成下述等价形式：

很显然，由方程(20)、 (21)可知饱和特性的闭环控制系统是线性切换系统，也可称为连续切换系统、 自治切换系统或离散事件连续系统，它包含2个子系统. 因此设计饱和最优PID控制器至少满足： 1) 在给定切换信号下，饱和最优PID控制器能够使得被控过程渐近稳定； 2) 饱和最优PID控制器能够使得给定的性能指标极小化. 那么饱和最优PID控制器的设计问题可用下述方程进行描述：

其中，Q是控制权重矩阵，Hasss是稳定切换系统集合，性能指标J具有误差的导数及高阶导数交叉项，涵盖了扩展误差平方积分(augmented integral squared error，AISE)性能指标[12, 13, 15]. AISE性能指标不包含误差导数的交叉项，约束(1)是闭环控制系统的状态约束，约束(2)是稳定性约束，约束(3)是子系统2的稳定性约束，约束(4)是最优PID控制器参数的可行域约束. 约束最优控制问题(22)得到求解，可获得相应的饱和最优PID控制器. 若闭环反馈系统对于任意切换信号都能保持渐近稳定，闭环反馈系统最终等价为线性切换系统. 根据共同李亚普诺夫函数定理[16, 17, 18]，那么约束最优控制问题(22)的稳定性约束(2)可等价转化为矩阵不等式或矩阵方程约束：

其中，矩阵P、 Q1、 Q2至少是半正定对称矩阵，它们满足代数李亚普诺夫矩阵方程： AT1P+PA1=-Q1，AT2P+PA2=-Q2，需要指出的是： 矩阵P、 Q1、 Q2它们是待定矩阵. 约束(2)保证了线性切换系统稳定性，对于任何切换信号都能使控制系统保持稳定，此时线性切换系统可等价于包含摄动参数的线性系统. 根据李亚普诺夫定理1、 2，性能指标J可以等价转化为如下形式：

为了保持李亚普诺夫矩阵方程(23)、 (24)的相容性，可选取适当的控制权重矩阵Q=Q1=Q2(Q=Q1 or Q=Q2)，故本文控制权重矩阵Q是待定矩阵. 应用李亚普诺夫定理1、 2，状态约束等价转化为代数方程约束. 子系统2的稳定性约束可以等价转化为

最优控制问题的性能指标及其约束条件都被转化为相应的不等式约束或方程约束，饱和最优PID控制器设计问题转化为非线性约束最优化(nonlinear constraint optimization，NLCO)问题. 应用共同李亚普诺夫函数定理和李亚普诺夫定理，最优控制问题转化为约束最优化问题. 因此解决下述非线性约束最优化问题，可获得相应的饱和最优PID控制器：

线性切换系统本质上属于非线性系统，通过应用相关定理将约束最优控制问题转化为非线性约束最优化问题. 通过寻求适当的对称矩阵P、 Q使得性能指标J极小化，其中反馈系统的初始状态x(0)=x0一般是非零向量. 通过解决非线性约束最优化问题(26)，可获得饱和最优PID控制器，目前很多最优化方法和最优化工具箱及相应软件例如牛顿法、 梯度法、 内点法、 遗传算法及粒子群算法等都能解决非线性约束最优化问题. 因此，通过最优化参数所满足代数关系，可获得相应的饱和最优PID控制器：

4 仿真结果及分析

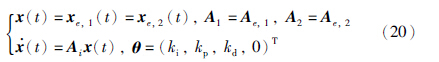
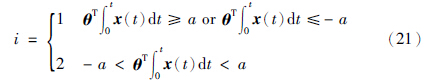
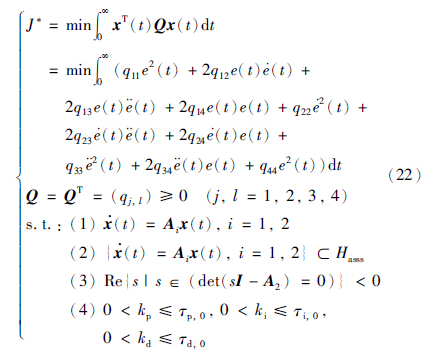
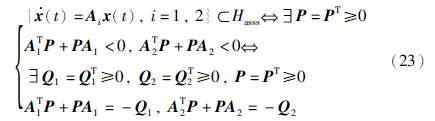
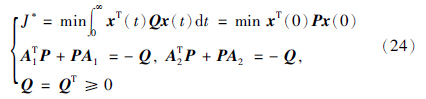
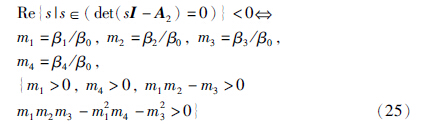
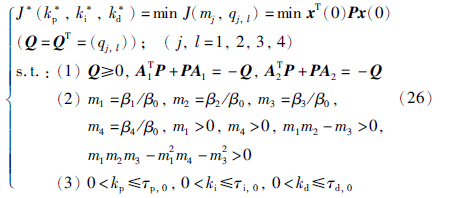
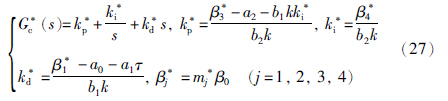
针对含有延时的低阶被控过程，本文提出了饱和最优PID控制器设计方法，含延时的2阶被控过程作为本文设计方法的示例. 本文的被控过程取自文[19, 20]的修改示例，其中的被控过程1是非最小相位过程，被控过程2是全极点被控过程.

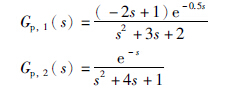
针对含延时的2阶被控过程，本文给出了被控过程1与被控过程2的饱和最优PID控制器参数. 其中表格1给出在不同控制权重与饱和特性参数情况下的最优PID控制器，由表格1的饱和最优PID控制器参数可知： 在饱和输出即控制器最大输出h固定时，饱和斜率k会直接影响最优PID控制器的参数优化，也会影响控制系统性能，特别是控制系统动态特性会受到直接影响. 控制权重矩阵在本文里是待定参数，因此需要参与控制器参数的最优化过程.

在不同的饱和最优PID控制器情况下，图 2、 3与图 4、 5分别给出本文被控过程1与被控过程2的单位阶跃响应结果及控制误差曲线. 对于被控过程1，图 2、 3响应结果及控制曲线表明： 饱和最优PID控制器动态性能较好，没有系统超调，延迟时间、 上升时间、 过渡过程时间都较小，但是在饱和斜率k=16时，阶跃响应情况及控制误差曲线发生了非常明显的变化. 对于被控过程1，饱和斜率k=16时，饱和最优PID控制器的比例增益非常小，导致响应速度过慢. 饱和最优PID控制器的比例增益过小，主要是由饱和斜率k增大所影响，当然控制权重也有一定影响，饱和斜率增大导致了响应速度过慢. 由此可知，饱和斜率会影响饱和最优PID控制器的参数优化.

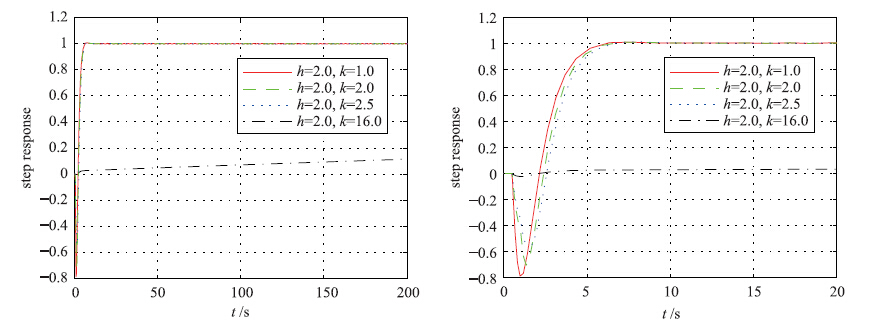图 2 被控过程1的饱和最优PID控制器阶跃响应Fig. 2 Step response of saturated optimal PID controller for controlled process 1
图选项
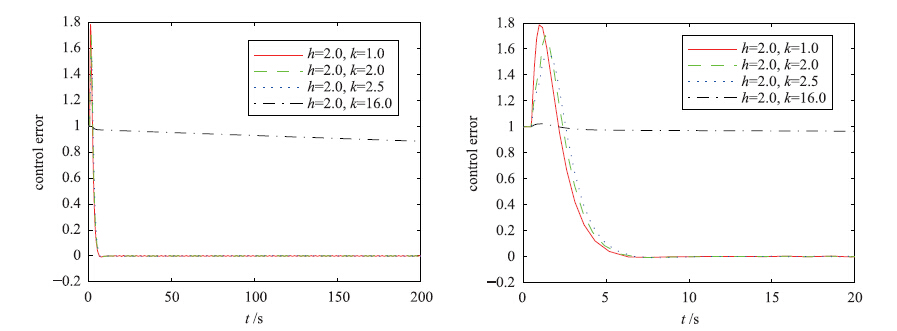图 3 被控过程1阶跃响应的控制误差Fig. 3 Step response′s control error of controlled process 1
图选项
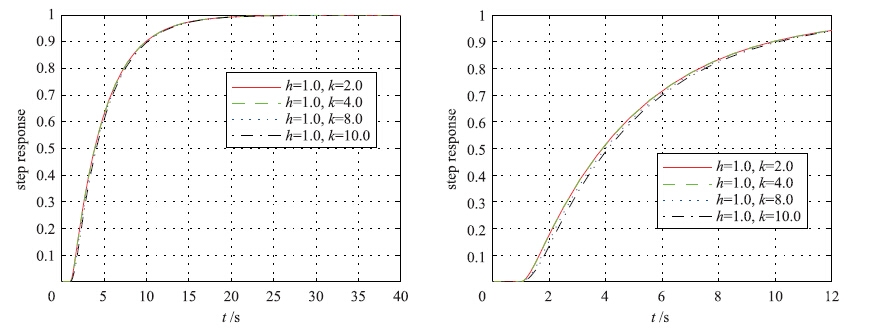图 4 被控过程2的饱和最优PID控制器阶跃响应Fig. 4 Step response of saturated optimal PID controller for controlled process 2
图选项
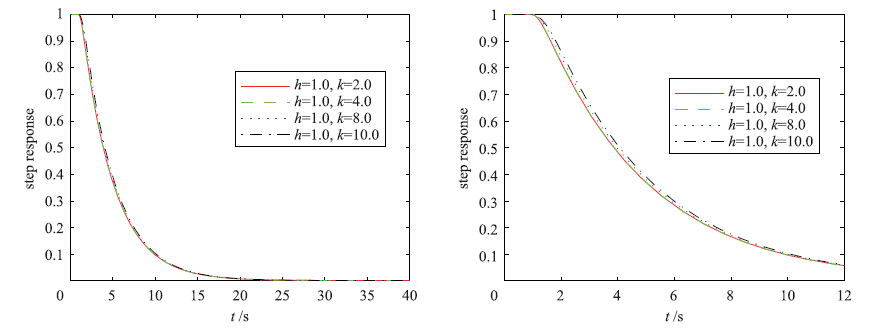图 5 被控过程2阶跃响应的控制误差Fig. 5 Step response′s control error of controlled process 2
图选项

对于被控过程2，图 4、 5响应结果及控制曲线表明： 饱和最优PID控制器动态性能较好，没有系统超调，延迟时间、 上升时间、 过渡过程时间都较小，即使在饱和斜率k=10时，阶跃响应情况及控制误差曲线都没有发生特别明显的变化.

针对被控过程1、 2，研究了不同PID调节方法的阶跃响应情况，其中图 6、 7显示了Z-N调节法与本文的饱和PID调节法的阶跃响应结果. 图 6、 7的阶跃响应结果表明： 对于被控过程1、 2，Z-N调节法响应较差，调节时间较长，出现不平滑振荡响应，具有较大超调等，本文的饱和PID调节法具有响应速度快，调节时间较小且响应曲线平滑、 无超调等优点.

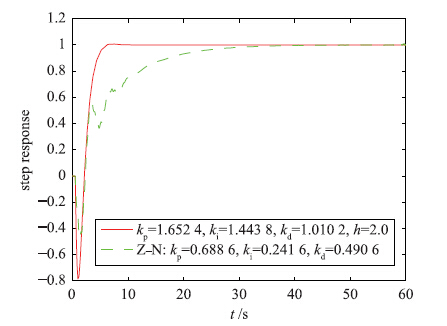图 6 被控过程1的不同PID调节方法的阶跃响应Fig. 6 Different PID tuning methods′ step
图选项
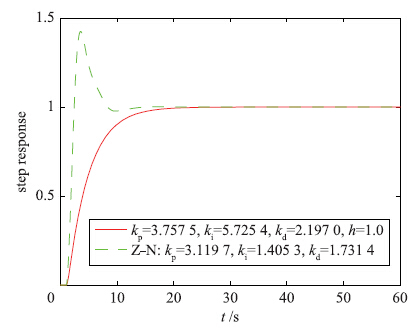图 7 被控过程2的不同PID调节方法的阶跃响应Fig. 7 Different PID tuning methods′ step response for controlled process 2
图选项

总之通过对比研究，由被控过程1与被控过程2可以知道，本文的饱和最优PID控制器设计方法，能提供较好的系统性能，可应用于最优PID控制器的综合与整定.

5 结论

针对控制器输出饱和问题和含延时的低阶过程，本文提出了一种非线性系统的饱和最优PID控制器设计方法，证明了带有饱和环节的闭环系统与线性切换系统或自治切换系统相等价. 本文给出了一种新的最优PID控制器设计指标，建立了非线性约束最优控制问题. 应用共同李亚普诺夫函数定理和李亚普诺夫定理，该最优控制问题被等价转化为非线性约束最优化问题. 数值求解相应的最优化问题，可获得饱和最优PID控制器，仿真结果表明了本设计方法的可行性和有效性. 本文的饱和最优PID控制器设计方法与传统最优控制器设计方法差异较大，且无需求解代数黎卡提方程. 未来研究工作将关注非线性鲁棒最优PID控制器设计.

表 1 含延时的二阶被控过程饱和最优PID控制器 Tab. 1 Saturated optimal PID controller for second-order process with time delay
Plantscontrol weight matrix Q=[q1 q2 q3 q4]
q1=(q11 q12 q13 q14)，q2=(q12 q22 q23 q24)，
q3=(q13 q23 q33 q34)，q4=(q14 q24 q34 q44)		optimal PID controllerparameter
h and k
k*pk*ik*d
Plant 1q1=(0 0 0 0.326 1)，q2=(0 0 0 1.671 8 )，
q3=(0 0 3.343 5 0)，q4=(0.326 1 1.671 8 0 0)		1.652 41.443 81.010 2h=2.0，k=1.0
q1=(0 0 0.356 0×10-2 1.206 3)，
q2=(0 0.712 0×10-2 0.040 7 0.114 5)，
q3=(0.356 0×10-2 0.040 7 0.229 0 0)，
q4=(1.206 3 0.114 5 0 0)		0.818 70.723 20.497 9h=2.0，k=2.0
q1=(0 0 0.262 3×10-2 0.702 6)，
q2=(0 0.524 6×10-2 0.081 2 0.594 0)，
q3=(0.262 3×10-2 0.081 2 1.188 0 0)，
q4=(0.702 6 0.594 0 0 0)		0.655 00.578 50.398 3h=2.0，k=2.5
q1=(0 0 0.226 4×10-2 0)，q2=(0 0.452 8×10-2 0 0)，
q3=(0.226 4×10-2 0 0 6.007 9)，q4=(0 0 6.007 9 0)		0.054 80.001 00.062 4h=2.0，k=16
Plant 2q1=(0 0 0 5.136 7)，q2=(0 0 0 0.715 2)，
q3=(0 0 1.430 4 0)，q4=(5.136 7 0.715 2 0 0)		3.757 55.725 42.197 0h=1.0，k=2.0
q1=(0 0 0 5.168 9)，q2=(0 0 0 1.102 6)，
q3=(0 0 2.205 2 0)，q4=(5.168 9 1.102 6 0 0)		1.690 12.729 51.005 2h=1.0，k=4.0
q1=(0 0 0 2.428 2)，q2=(0 0 0 0.396 2)，
q3=(0 0 0.792 5 0)，q4=(2.428 2 0.396 2 0 0)		0.551 70.974 20.619 8h=1.0，k=8.0
q1=(0 0 0 2.455 8)，q2=(0 0 0 0.371 6)，
q3=(0 0 0.743 3 0)，q4=(2.455 8 0.371 6 0 0)		0.440 90.802 70.536 5h=1.0，k=10.0
表选项
参考文献
[1] Astrom K J,Hagglund T. PID controller theory,design and tuning[M]. Santa Barbara,CA,USA: Instrument Society of America,1995.
[2] Ziegler J G,Nichols N B. Optimum settings for automatic controllers[J]. ASME Transactions,1942(64): 759-768.
[3] Cohen G H,Coon G A. Theoretical consideration of related control[J]. ASME Transactions,1953(75): 827-834.
[4] 彭富明,方斌. 含死区和饱和的非线性系统PID控制器设计[J]. 兵工学报,2013,34(10): 1298-1303. Peng F M,Fang B. Design of PID controller for nonlinear system with dead-zone and saturation[J]. Acta Armamentarii,2013,34(10): 1298-1303.
[5] 章萌,李爱军,刘世民. 弹性飞机的混合H2/H∞最优PID控制器参数优化[J]. 振动与冲击,2011,30(10): 197-202. Zhang M,Li A J,Liu S M. Parametric optimization for mixed H2/H∞optimal PID controller of a flexible aircraft[J]. Journal of Vibration and Shock,2011,30(10): 197-202.
[6] Bianchi F D,Mantz R J,Christiansen C F. Multivariable PID control with set-point weighting via BMI optimization[J]. Automatica,2008,44(2): 472-478.
[7] 夏思为,段书凯,王丽丹,等. 基于忆阻神经网络PID控制器设计[J]. 计算机学报,2013,36(12): 2577-2586. Xia S W,Duan S K,Wang L D,et al. Design of memristive neural network PID controller[J]. Chinese Journal of Computers,2013,36(12): 2577-2586.
[8] Saeki M. Fixed structure PID controller design for standard H∞control problem[J]. Automatica,2006,42(1): 93-100.
[9] Madhuranthakam C R,Elkamel A,Budman H. Optimal tuning of PID controllers for FOPTD,SOPTD and SOPTD with lead processes[J]. Chemical Engineering and Processing,2008,47(2): 251-264.
[10] Dickinson P B,Shenton A T. A parameter space approach to constrained variance PID controller design[J]. Automatica,2009,45(3): 830-835.
[11] Kim T H,Maruta I,Sugie T. Robust PID controller tuning based on the constrained particle swarm optimization[J]. Automatica,2008,44(5): 1104-1110.
[12] Li X H,Yu H B,Yuan M Z. Design of an optimal PID controller based on Lyapunov approach[C] //Proceedings of International Conference on Information Engineering and Computer Science. Piscataway,NJ,USA: IEEE,2009: 1-5.
[13] Li X H,Yu H B,Yuan M Z,et al. Design of robust optimal proportional-integral-derivative controller based on new interval polynomial stability criterion and Lyapunov theorem in the multiple parameters' perturbations circumstance[J]. IET Control Theory and Applications,2010,4(11): 2427-2440.
[14] Li X H,Yu H B,Yuan M Z. A new design method of optimal PID controller with dynamic performances constrained[J]. Control and Intelligent Systems,2012,40(4): 1-21.
[15] Li X H,Yu H B,Yuan M Z. Design of optimal PID controller with ε-routh stability for different processes[J]. Mathematical Problems in Engineering,2013(1): 1-22.
[16] Dayawansa W P,Martin C F. A converse Lyapunov theorem for a class of dynamical system which undergo switching[J]. IEEE Transactions on Automatic Control,1999,44(4): 751-760.
[17] Mancilla-Aguilar J L,Garcia R A. A converse Lyapunov theorem for nonlinear switch system[J]. System and Control Letters,2000,41(1): 67-71.
[18] Narendra K S,Balakrishnan J. A common Lyapunov function for stable LTI system with commuting A-matrices[J]. IEEE Transactions on Automatic Control,1994,39(12): 2469-2471.
[19] D'azzo J J,Houpis C H. Linear control system analysis and design[M]. 2nd ed. New York,USA: McGraw-Hill,1981.
[20] Tong M D. Linear system theory and design[M]. Hefei: University of Science and Technology of China Press,2004.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0043
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

李先宏, 于海斌, 曾鹏, 苑明哲, 孙兰香
LI Xianhong, YU Haibin, ZENG Peng, YUAN Mingzhe, SUN Lanxiang
低阶被控过程含延迟的饱和最优PID控制器设计方法
A Design Method of Saturated Optimal PID Controller for the Low-order Controlled Processes with Time Delay
信息与控制, 2015, 44(1): 43-50.
INFORMATION AND CONTROL, 2015, 44(1): 43-50.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0043

文章历史

收稿日期：2014-06-23
录用日期：2014-08-25
修回日期：2014-09-10

工作空间