文章快速检索  
  高级检索
引用本文
王文庆, 杨振新. 基于Mamdani的通用模糊逼近器的设计与实现[J]. 信息与控制, 2015, 44(1): 51-55
WANG Wenqing, YANG Zhenxin. Design and Implementation of a Universal Fuzzy Approximator Based on Mamdani System[J]. INFORMATION AND CONTROL, 2015, 44(1): 51-55.
基于Mamdani的通用模糊逼近器的设计与实现
王文庆, 杨振新    
西安邮电大学自动化学院, 陕西 西安 710061
收稿日期: 2013-12-23; 录用日期: 2014-03-10; 修回日期: 2014-03-20
基金项目：国家自然科学基金资助项目（61305098）.
作者简介: 王文庆（1964-），男，博士，教授. 研究领域为复杂系统结构分析与鲁棒控制，智能信息处理.
杨振新（1988-），男，硕士生. 研究领域为智能信息处理.
通讯作者：杨振新，303897198@qq.com
摘要：研究利用未知系统的输入输出数据，自适应构造一个满足对未知系统逼近精度要求的模糊系统．提出了基于二分搜索算法的改进算法，优化了模糊系统的规则数目，得到一组准确地满足精度要求的规则数上限．从算法运行时间的角度分析了算法的复杂度，并给出了估算算法运行时间的公式．仿真结果表明，该方法是可行并且有效的．
关键词： 模糊逻辑系统     通用逼近     二分算法     算法复杂度    
Design and Implementation of a Universal Fuzzy Approximator Based on Mamdani System
WANG Wenqing, YANG Zhenxin     
Xi'an University of Posts and Telecommunications, Xi'an 710061, China
Abstract:Based on input/output (I/O) data of an unknown system,a new method for constructing a fuzzy system adaptively,which meets the accuracy requirements of the system,is put forward. To optimize the system rules,a new algorithm based on the binary search algorithm is designed,which can obtain an upper limit of rules to meet the accuracy requirements. Subsequently,the complexity of the algorithm is analyzed from the perspective of the algorithm running time,and the formula for estimating running time of the algorithm is proposed. The simulation data shows that the method is feasible and effective.
fuzzy logic system     universal approximation     binary algorithm     algorithm complexity    

1 引言

模糊逻辑系统(FLS)的理论已广泛应用在模糊辨识和模糊控制上. 与经典控制相比，它可以直接实现复杂系统的非线性建模； 与其它智能建模相比，它能有效地利用语言信息[1]. 利用模糊逻辑系统，实现对非线性模型的辨识是一个重要问题.

文[2]从输入输出数据提取模糊规则，采用最小二乘法解模糊，缺点是需通过人为的反复试验来确定模糊集个数，文[3]提出了一种在遗传算法中融入误差反向传播学习算法的混合学习算法来优化参数，并以二分算法优化结构. 文[4, 5]通过递推模糊聚类法来自适应调整模糊模型，并用卡尔曼滤波方法实时估计模型的时变参数，实现了一种在线辨识方法； 文[6]使用C均值聚类算法及递推最小二乘法确定模型的前后件参数，提出一种基于递阶分解聚类的递推模糊辨识方法. 文[7]提出一种基于新的模糊模型和加权递推最小二乘算法(WRLSA)的非线性系统模糊辨识方法.

但是，这些研究主要集中在理论分析方面，特别是对具体的实现算法以及算法的有效性、 通用性等方面相关文献并不多. 文[8, 9, 10, 11, 12, 13]等都是成功应用模糊系统逼近非线性不确定项的例子，但其实现都是针对特定问题，且算法的效率也没有讨论. 一旦被逼近对象发生变化或者改变精度时，就得重新定义隶属函数，手动构造模糊系统. 此外，根据经验主观设置隶属函数或调整隶属函数参数的情况也影响了模糊系统的逼近效率.

本文研究基于Mamdani模糊系统的通用逼近器的实现算法，完成对未知系统的自适应快速辨识，并对通用逼近器实现算法的复杂度做出定量分析.

2 FLS的结构及性质 2.1 模糊系统的基本组成

Mamdani模糊系统由模糊产生器、 模糊规则库、 模糊推理机及模糊消除器4部分构成，其基本组成如图 1所示.

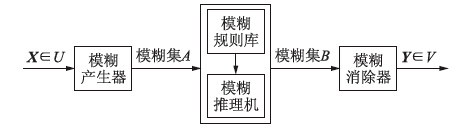图 1 模糊系统Fig. 1 Fuzzy system
图选项

系统中模糊产生器的作用是将输入论域U内的一个确定点X=(x1，x2，…，xn)映射为U上的一个模糊集合A； 然后由模糊推理机根据模糊规则库中的“如果—则”规则，推理得到模糊集合B，即实现U1×U2×…×Un上的模糊集合到V上的模糊集合的映射. 最后，由模糊消除器把V上的模糊集合B映射为一个确定的点Y∈V.

2.2 模糊逻辑系统的通用逼近性质 2

Mamdani型模糊系统已被证明可作为未知函数的通用逼近器[14]，一个采用单点模糊化、 乘积推理规则、 中心平均解模糊方式的模糊系统[15]由输入X=(x1，x2，…，xn)T∈U产生的输出Y∈V可以表示为

其中，θl为式(1)模糊规则组成的模糊规则库中第l条规则的“则”部分对应的模糊集合Al的中心，即隶属函数μAlιi(xi)在θl这点取得最大值(1≤l≤N). FLS具有万能逼近性质，即模糊系统能以任意精度逼近紧集上的任意函数. 设g(x)是有界闭集U上的实连续函数，那么对于任意给定的正数ε，一定存在如式(1)的模糊逻辑系统，使得

式(1)的模糊系统是万能逼近器，表明只要有足够多的规则，必然能实现对连续函数的逼近.

3 通用逼近器的设计 3.1 逼近算法思想

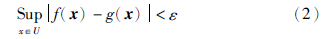
FLS可以作为万能逼近器，但是学者并没有给出如何去确定规则数构造FLS. 规则太少时，这样的系统精度往往达不到要求； 规则太多时，规则会存在冗余，并且系统实现变得非常复杂. 如何以最小规则数实现对未知函数的逼近，以及算法实现可行性的研究就显得尤为重要. 本节就是依据FLS的存在性定理，找到这样一组最优规则.

传统二分算法采用分治策略，在一个有限有序序列中搜索目标，不断将序列进行对半分割，每次拿中间元素和目标元素进行比较，直到找到为止. 而实现模糊逼近时，目标规则数并不具有先知性，传统的二分算法并不能直接用于该模型. 因此，本文对传统的二分算法进行了改进，加入了标志位，如果运算满足条件，置标志位True，否则置为False. 这样就可以通过标志位确定规则的范围，逐步收缩自下而上构造一棵满二叉树，如图 2所示. 树的深度即为得到最优规则的次数.

图 2 规则收缩Fig. 2 Contraction of rule
图选项
3.2 通用逼近算法的实现

步骤1： 规则增长，确定规则数的范围

令初始规则数为2，并以2的指数n线性增长使规则数迅速膨胀，直到逼近误差μ小于逼近精度ε，得到一组满足逼近精度ε的规则数上限2n，即满足逼近精度的最小规则数在(2n-1，2n］这样一个左开右闭区间.

步骤2： 规则收缩，得到一组满足逼近精度的规则数

在规则区间(2n-1，2n］范围，利用二分查找算法，对规则数进行收缩. 每一次执行二分算法得到的规则如果满足逼近精度，置标志位为True，否则，置为False. 显然，搜寻次数(即标志位个数)等于根节点的层数，最后一次标志位为True时对应的规则数即最优规则数. 另外，如果标志位全为False，2n即最优规则数. 此时就得到了一组等值的规则数Ni，i∈(1，2，…，n).

步骤3： 规则优化，分析得到一组相对最优的规则数

令规则数N1采用改进的二分算法优化，其它规则Ni，i≠1保持不变，迭代计算即可得到优化后的规则数N1. 再对规则数N2采用改进的二分算法优化，其它规则数Ni，i≠2保持不变，可以得到优化后的规则数N2. 依此类推，相对最优的Ni条规则即可实现对未知函数的逼近.

3.3 算法复杂度分析

一个有效的通用逼近器除保证其在理论上必须收敛之外，其实现算法也必须有效且复杂度能够预见，在保证逼近精度的条件下用现有的硬件可以实现. 一般的，一个算法的复杂度由其时间复杂度和存储复杂度来度量. 由于硬件的技术足以满足，该模型中存储的问题已不存在，本文从时间复杂度角度进行分析.

由3.2节提到的基于二分算法的通用逼近算法分析，得到该构造方法的算法复杂度为

其中n表示循环的次数，m表示维数.

在每一次逼近过程中，算法的执行涉及到加法、 减法、 乘法、 除法以及比较等基本运算. 为便于估算其可行性，可通过运行时间T(s)衡量算法的时间复杂度[16]：

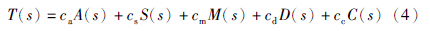
式中： ca、 cs、 cm、 cd、 cc分别为一次加、 减、 乘、 除、 比较和交换操作所需时间，函数A(s)、 S(s)、 M(s)、 D(s)、 C(s)分别为算法中加、 减、 乘、 除和比较操作的次数.

对于式(1)表示的模糊逼近器模型，假设论域x1，x2，…，xn上的采样点个数分别为k1，k2，…，kn，规则间隔d1，d2，…，dn，论域长度为l1，l2，…，ln，规则数分别为N1，N2，…，Nn. 对于每一次逼近算法：

(1) 构造三角形隶属函数，需做n次除法得到规则间隔d1，d2，…，dn，然后做次加法得到各个顶点.

(2) 对于模糊推理及解模糊运算，需做3×(Ni×ki)次乘法运算，2×(Ni×ki)次加法运算，ki次除法运算.

(3) 计算逼近误差，需要做ki次减法得到单点误差，再求无穷范数，需做ki次加法运算，ki次比较运算.

对于整个自适应模糊逼近过程：

(1) 规则增长，每次循环需要做1次除法及1次比较运算.

(2) 二分算法，每次循环需要做1次加法和1次除法及1次比较运算.

因此，每一次模糊逼近的运算次数可记为

整个过程，规则增长n1次，规则缩减n2次，记为

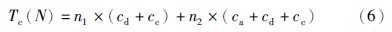
该通用逼近器的运行时间为

4 仿真实验

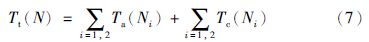
例： 考虑一组2维输入单输出空间的I/O数据的逼近问题，提取函数g(x1，x2)=sinx1×cosx2的41对输入输出数据作为测试样本，其中定义域取｛(x1，x2)1≤(x1-2)2+x22≤4｝，误差限ε=0.1.

4.1 设计一个基于三角形隶属函数的模糊系统

(1) 在[αi，βi]上定义Ni(i=1，2)个一致的、 完备的模糊集A1i，A2i，…，ANii，它们具有三角形隶属函数μA1i(xi，a1i，b1i，c1i)，…，μANii(xi，aNii，bNii，cNii)，且A1i2i<…Nii，其中a1i=b1i=αi，bNii=cNii=βi. 定义e11=α1，eN11=β1，ej1=，j=2，3，…，N1-1. 类似地定义e12=α2，eN22=β2，ej2=，j=2，3，…，N2-1. 这样定义的模糊集在N1=4，N2=4，α1=0，α2=-2，β1=4，β2=2时，如图 3所示.

图 3 模糊系统设计Fig. 3 Fuzzy system design
图选项
(2) 建立N1×N2条如下模糊规则

Ri1i2： if x1 is Ai11 and x2 is Ai22 then y is Bi1i2，其中i1=1，2，…，N1，i2=1，2，…，N2，将模糊集Bi1i2的中心选择为i1i2=g(ei11，ei22)，即图 2中的16个黑点.

(3) 用乘积推理机、 三角形模糊器和中心平均解模糊器，根据N1×N2条规则构造的模糊系统为

4.2 逼近算法的实现

步骤1： 初始规则数N1=N2=2，并以2n方式增长，n∈｛1，2，…，n｝. 当在第n次运算后，误差值μ恰好小于逼近精度ε，迭代停止. 此时，规则数N1=N2=2n为满足逼近精度的规则数. 上式要满足逼近精度ε＜0.1，迭代得到当n=5时，μ=0.0336小于逼近误差ε=0.1，也就是说N1=N2=32条规则即可满足逼近精度，规则区间为(16，32］.

步骤2： 由上面步骤可得上限max=25满足逼近精度的规则，下限min=24则不满足，取规则数middle==24，利用2.3.1节算法进行循环迭代，就能得到满足条件的最优规则数. 此例中规则数的取值middle依次为｛24，20，18，19｝，标志位flag对应的值依次为｛True，True，False，False｝. 因此，当规则数N1=N2=20时，恰好满足逼近条件.

步骤3： 先保持N1=20不变，N2=32，此时取max=32，min=0，middle=16，用二分算法，middle的取值依次为｛16，24，20，18，19｝，标志位flag对应的值依次为｛False，True，True，False，False｝，因此，N2的最小值为20. 再保持N2=20不变，N1=32，此时max=32，min=0，middle=16，用二分算法，middle的取值依次为｛16，24，20，18，17｝，标志位得到对应的值依次为｛False，True，True，True，False｝，因此，N1的最小值为18. 即N1×N2=18×20条规则，就能满足逼近精度ε=0.1，此时逼近误差为μ=0.0994.

4.3 小结

本文在酷睿双核处理器PC机、 Windows 7系统、 Matlab 2010环境下做了仿真，结果如下： 图 4为待逼近的原函数图，图 5为18×20条规则下完成模糊逼近的图，图 6描述了各个数据点的逼近误差，图 7描述当精度ε=0.1时，本文算法与递增算法在相同的学习次数下逼近误差对比.

图 4 原函数图Fig. 4 Original function
图选项
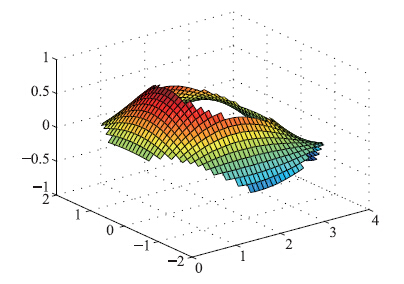图 5 仿真结果Fig. 5 Simulation result
图选项
图 6 逼近误差Fig. 6 Approximation error
图选项
图 7 误差对比Fig. 7 Error comparison
图选项

在相同的规则数目下，对两种算法仿真结果做了比较. 从表 1看出，本文所提算法的学习次数明显优于递增法，运行时间有效提升.

表 1 相同规则数的效率 Tab. 1 Efficiency under the same number of rules
仿真方法规则数学习次数运算时间/s时间复杂度逼近误差
递增法20×20192.1883O(n)0.0697
18×20234.6285O(n)0.0994
本文算法20×2091.7821O(lbn)0.0697
18×20133.3769O(lbn)0.0994
表选项

在不同的精度要求下，对两种算法仿真结果做了比较. 从表 2看出，对于精度要求越高时，本文算法的收敛速度优势越明显.

表 2 不同精度的效率 Tab. 2 Efficiency under different accuracies
仿真方法误差精度规则数学习次数运算时间/s逼近误差
递增法0.120×20192.18830.0697
0.0528×28275.17390.0443
本文算法0.120×2091.78210.0697
0.0528×2892.29210.0443
表选项
5 总结

本文利用输入输出数据构造模糊逻辑系统时，采用规则以指数增长快速构造模糊逻辑系统，本例中，5次运算就实现了对未知系统的逼近，特别适合对存储量不做特别限制的系统. 而对于存储量受限的系统，提出一种带标志位的二分算法，实现了以最小的模糊规则满足逼近要求. 最后做了算法复杂度分析，给出估算算法运行时间的公式. 仿真结果表明，这种快速构造和优化方法是可行和高效的.

参考文献
[1] 王辉,肖建,严殊. 关于模糊系统辨识近年来的研究与发展[J]. 信息与控制,2004,33(4): 445-450. Wang H,Xiao J,Yan S. Recent research and development on fuzzy system identification[J]. Information and Control,2004,33(4): 445-450.
[2] 邓建军,徐立鸿,吴启迪. 一种模糊逻辑系统的快速学习算法[J]. 信息与控制,2001,30(6): 555-557. Deng J J,Xu L H,Wu Q D. Fast learning algorithm for fuzzy logic system[J]. Information and Control,2001,30(6): 555-557.
[3] 王宏伦,吕庆风,佟明安. 模糊逻辑系统的快速构造与优化[J]. 控制与决策,2000,15(4): 451-454. Wang H L,Lü Q F,Tong M A. Fast construction and optimization of fuzzy logic systems[J]. Control and Decision,2000,15(4): 451-454.
[4] 静大海,刘晓平. 一种非线性模型的在线辨识方法[J]. 控制工程,2007,14(5): 482-484. Jing D H,Liu X P. Online identification method for nonlinear models[J]. Control Engineering of China,2007,14(5): 482-484.
[5] 王娜,杨煜普. 一种基于改进客观聚类分析的模糊辨识方法[J]. 控制与决策,2009,24(1): 13-17. Wang N,Yang Y P. A fuzzy identification method based on the enhanced objective cluster analysis[J]. Control and Decision,2009,24(1): 13-17.
[6] 王广军,王志杰,陈红. 基于递阶分解聚类的非线性系统递推模糊辨识[J]. 控制与决策,2009,24(12): 1846-1850. Wang G J,Wang Z J,Chen H. Recursive fuzzy identification of nonlinear systems based on hierarchical decomposing clustering[J]. Control and Decision,2009,24(12): 1846-1850.
[7] 刘福才,关新平,裴润. 基于一种新模糊模型的非线性系统模糊辨识[J]. 控制理论与应用,2003,20(1): 113-116. Liu F C,Guan X P,Pei R. Fuzzy identification based on new fuzzy model for nonlinear systems[J]. Control Theory & Applications,2003,20(1): 113-116.
[8] 王文庆,佟明安. 一类复杂控制系统分散自适应鲁棒控制器设计[J]. 控制理论与应用,2004,20(6): 884-888. Wang W Q,Tong M A. Decentralized adaptive robust controller design for a class of complex systems[J]. Control Theory & Applications,2004,20(6): 884-888.
[9] Elshafei A L. Robust longitudinal aircraft control based on an adaptive fuzzy logic algorithm[J]. Control and Intelligent Systems,2003,31(2): 63-70.
[10] Zhou S,Feng G,Feng C B. Robust control for a class of uncertain nonlinear systems: Adaptive fuzzy approach based on backstepping[J]. Fuzzy Sets and Systems,2005,151(1): 1-20.
[11] Shin J H. Robust adaptive fuzzy backstepping control for trajectory tracking of an electrically driven nonholonomic mobile robot with uncertainties[J]. Journal of Institute of Control,Robotics and Systems,2012,18(10): 902-911.
[12] Dong C,Xu L,Chen Y,et al. Networked flexible spacecraft attitude maneuver based on adaptive fuzzy sliding mode control[J]. Acta Astronautica,2009,65(11): 1561-1570.
[13] Liang X,Yang B,Wang Y. Simulation and test of trajectory tracking control for tomato harvesting manipulator based on fuzzy logic compensation[J]. Transactions of the Chinese Society of Agricultural Engineering,2013,29(17): 16-23.
[14] 曾坷,徐文立,张乃尧. 特定Mamdani模糊系统的通用逼近性[J]. 控制与决策,2000,15(4): 435-438. Zeng K,Xu W L,Zhang N Y. Universal approximation of special Mamdani fuzzy systems[J]. Control and Decision,2000,15(4): 435-438.
[15] 王立新. 模糊系统与模糊控制教程[M]. 北京: 清华大学出版社,2003: 102-104. Wang L X. A course in fuzzy systems and control[M]. Beijing: Tsinghua University Press,2003: 102-104.
[16] Sahni S. Data structures,algorithms,and applications in C++[M]. Boston,USA: WCB/McGraw-Hill,1998: 17.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0051
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

王文庆, 杨振新
WANG Wenqing, YANG Zhenxin
基于Mamdani的通用模糊逼近器的设计与实现
Design and Implementation of a Universal Fuzzy Approximator Based on Mamdani System
信息与控制, 2015, 44(1): 51-55.
INFORMATION AND CONTROL, 2015, 44(1): 51-55.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0051

文章历史

收稿日期：2013-12-23
录用日期：2014-03-10
修回日期：2014-03-20

工作空间