1 引言
工程机械系统正向着轻质、 高速、 大型和复杂方向发展,在对此类系统进行控制时,需要同时考虑其部件大范围运动以及部件本身的结构变形,将其建模为刚柔耦合多体系统[1, 2, 3]. 它紧密结合航天器、 复杂机构等高科技领域的动力学与控制研究,对工业现代化发展具有十分重要的应用价值.
对于此类工程系统,为了得到较好的控制效果,则需要建立较为准确的模型. 刚柔耦合系统的理论建模主要经历了KED(kineto-elasto dynamics method)方法、 零次近似模型、 动力刚化和一次近似模型4个阶段[4]. 这些方法建模过程都较为复杂,有些方法所建模型阶次较高. 对此,本文将引入特征建模的思想. 由吴宏鑫院士提出的特征建模[5]就是根据对象动力学特征和控制性能要求相结合进行建模,模型形式比原动力学方程简单,工程容易实现. 并且特征模型与高阶系统的降阶模型不同,它是把高阶模型的有关信息都压缩到几个特征参量之中,不会丢失信息.
目前对刚柔耦合系统的控制方案主要有PID控制、 最优控制、 鲁棒控制、 自适应控制、 滑模变结构控制等. 陈炜[6]利用PID方法进行欠驱动平面柔性机械臂的控制分析和实验研究,但PID控制鲁棒性不是很强. Asghar[7]等将柔性航天器建模为线性欠阻尼弹性系统,将bang-bang控制问题转化为参数优化问题,降低了柔性附件的耦合诱发振动,此类控制较大程度依赖于系统精确的模型. Yang[8]等针对XTE(crosstrack error)卫星偏航回路的姿态控制回路根据刚体模型设计H2/H∞控制器,将柔性模态视为未建模动态,此类控制为了避免柔性模态对系统稳定性的影响,牺牲了控制性能. 滑模控制简单、 动态性能好但稳态性能差,适用于动态控制. 自适应控制对静态和动态特性都很有效,特别有很高的稳态精度,适用于静态控制. 模糊推理算法复杂,适用于协调级或组织级的控制. Li[9]等综合了自适应控制、 滑模控制和模糊方法各自的优点提出自适应变结构混杂控制方案,实现了较好的控制效果.
本文综合特征建模、 自适应控制以及滑模控制各自的优点,在特征建模基础上,提出一种基于PID滑模面的自适应离散滑模控制. 选择PID形式的滑模面可以有效抑制抖振,所设计控制器不仅可以实现对角位移快速跟踪控制,而且能够避免激发柔性部件的长时间振动. 最后通过物理实验验证了所设计控制器的有效性. 2 动量交换刚柔耦合多体系统特征建模
相对于惯性参考系,定义逆时针方向为转动正方向,主体转动惯量为Jh,转角为θ,动量轮转动惯量为J,转速Ω. 电机控制电压与主角度的传递函数(可参文[10])为
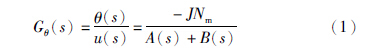

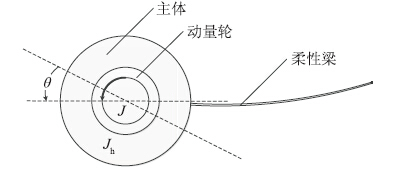 |
| 图 1 动量交换系统示意图Fig. 1 The diagram of momentum exchange system |
F=[f1 f2 … fN]T为柔性梁与中心刚体耦合系数向量,N为柔性梁前N阶模态,D为阻尼矩阵,u(s)为电机控制电压. 由传递函数可知,对象为一个线性定常系统. 孟斌等[11]给出了线性定常系统特征模型的证明,吴宏鑫等在文[5]中对高阶线性定常系统的特征建模进行了较为详细的阐述. 因而可以对此对象进行特征建模,特征模型可以用一个2阶时变差分方程描述

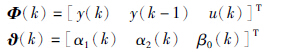
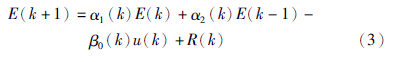
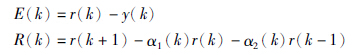
选择滑模面为如下形式
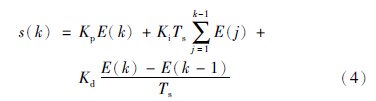
为了更好地分析滑模抖振,文[12]引入了滑模切换带宽度. 由(3)式可以得到离散滑模切换带宽度为


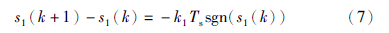

可以看出(7)式为一个常数. 这说明系统会在-k1Ts和k1Ts之间来回产生抖振. 从(4)式可以看出,带宽将随着偏差E(k)的减小而减小,而当E(k-1)→0时,Δ→0. 所以说,类似PID滑模的渐近稳定的离散滑模控制都能较好地抑制抖振.
3.2 基于PID滑模面的位置控制器设计由(4)式可以得到k+1时刻的滑模面为
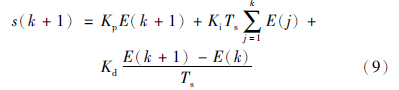
由于(3)式中的β0(k)的符号可正可负,对控制量影响较大,进而影响控制效果. 将β0(k)变为λ+β0(k),保证其为正,即有条件

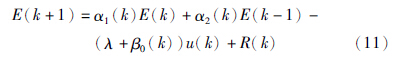
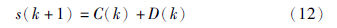

离散系统进入理想滑动模态时,滑模面满足s(k+1)=0[13],进而得到离散滑模的等效控制为
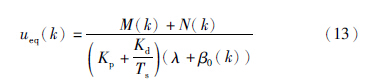
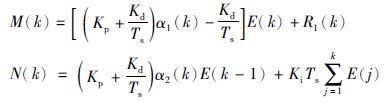
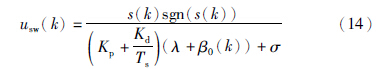
则总控制量为
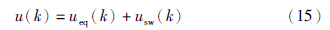
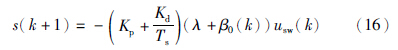
特征模型建立过程中,核心就是特征参数的辨识,通常采用递推最小二乘法进行辨识. 但是递推最小二乘方法运算量较大,不适用于微控制器; 如果系统受外部干扰,辨识参数波动幅度较大. 而另外一种辨识方法为改进的梯度法——随机递推梯度法[5, 14, 15],相对最小二乘方法可以节省计算量,可以应用到微控制器; 辨识参数受外部干扰的影响没有递推最小二乘法大. 当然随机梯度法也存在不足,如参数收敛缓慢、 收敛值随初值不同而不一样等. 但是,特征建模的一个很大的特点是可以事先确定参数范围,因此在初始阶段预先可确定参数初值. 在文[16]中提到的参数投影则可以确保参数在有效范围内. 对此,本文将采用随机梯度法对特征参数进行辨识.
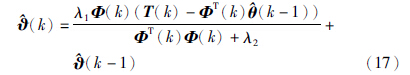
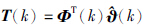 ,λ1和λ2根据干扰量大小和收敛速度要求选定,一般0<λ1<1和0<λ2<4.
,λ1和λ2根据干扰量大小和收敛速度要求选定,一般0<λ1<1和0<λ2<4. 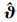 (k)=
(k)=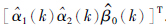 . 条件(10)式可以重写为
. 条件(10)式可以重写为

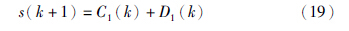

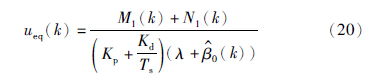
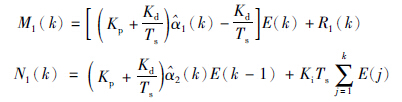
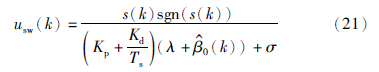
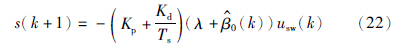
离散滑模控制器稳定性的证明,只需证明滑模面存在并可达. 如果离散滑模面满足如下条件,自适应离散滑模控制的准滑模运动是存在并且可达的[12, 17].
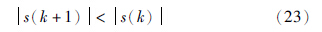
针对本文所提自适应滑模控制器的稳定性证明问题,采用李亚普诺夫相关知识来证明.
定义李亚普诺夫函数为


为了消除辨识参数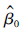 0(k)对系统稳定性的影响,保证系统稳定,引入了条件(18)式λ+
0(k)对系统稳定性的影响,保证系统稳定,引入了条件(18)式λ+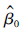 0(k)>0. 由于σ>0,故而有V(k+1)<V(k).
0(k)>0. 由于σ>0,故而有V(k+1)<V(k).
Hub-beam构型柔性多体实验系统如图 2所示. 实验系统由4大部分组成: 机械模块、 支架、 调理/功放模块和控制计算机. 控制计算机发出的激励信号或控制信号,经过功率放大器进行功率放大后驱动力矩电机,在电机转矩作用下,电机连同与电机底座刚性连接的托盘、 上下壳体、 柔性梁一同转动,由安装在底座的角位移传感器测量转角. 角位移传感器的输出经过调理电路进行滤波和适当变换后送入控制计算机. 柔性梁表面粘贴压电传感器测量悬臂梁的诱发振动,并通过调理电路进行滤波、 放大后送入控制计算机. 图 3为实验系统实物图. 表 1为实验系统相关参数.
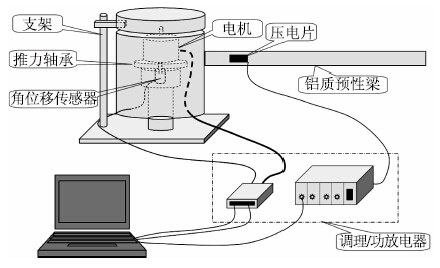 |
| 图 2 实验系统示意图Fig. 2 Schematic of experimental system |
 |
| 图 3 实验系统实物图Fig. 3 The physical map of experimental system |
| 参数名称 | 参数值 | 参数名称 | 参数值 |
| 电荷放大器 | YE852A | 中心刚体直径 | 20 cm |
| AD/DA板卡 | PCI1710 | 中心刚体高度 | 18 cm |
| 力矩电机 | 70Y53 | AD/DA采样率 | 400 Hz |
| 功率放大器 | OPA548T | 压电片型号 | p-42 |
| 压电片尺寸 | 3×1.5×1 cm3 | ||
| 柔性梁尺寸 | 90×3×0.15 cm3 | ||
刚柔耦合系统中心刚体期望转角θd=45°. 基于特征建模的滑模控制器参数: Ts=0.002 5 s,λ1=0.8,λ2=0.4,Kp=0.01,Ki=0.000 4,Kd=0.000 005,λ=0.5,σ=2.
PI控制器参数: 比例增益kp=0.25,积分增益ki=0.15. 模糊自适应PI控制器: 模糊输入为偏差(e)和偏差变化率(ec). 输出为比例系数变化量(Δkp)和积分系数变化量(Δki); 参数调整可以表示为kp=kp0+Δkp以及ki=ki0+Δki,kp0=0.25,ki0=0.15; 本文参考文[18, 19],经过多次实验所得较好的参数以及模糊规则如下: 偏差输入量化因子Ge=0.02,偏差变化率输入量化因子Gec=0.4,输出比例量化因子GΔkp=0.04,输出积分量化因子GΔki=0.055.
模糊分类为NB、 NM、 NS、 ZO、 PS、 PM、 PB,分别代表负大、 负中、 负小、 零、 正小、 正中、 正大,隶属函数采用三角函数. 模糊规则如表 2和表 3所示.
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PS | PB | PS | PB | PM | ZO | ZO |
| NM | PS | PB | PS | PM | PM | ZO | NS |
| NS | PB | PB | PB | PB | ZO | NS | NS |
| ZO | PB | PM | PB | ZO | NS | NB | NB |
| PS | ZO | PM | NS | NS | NB | NB | PM |
| PM | NS | ZO | NB | NB | NB | NM | PM |
| PN | ZO | NB | ZO | NB | NB | NM | NM |
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PS | NB | NS | NB | NB | NM | PS |
| NM | PS | NB | NS | NM | NM | NS | ZO |
| NS | ZO | ZM | NS | NM | NS | NS | ZO |
| ZO | ZO | NS | NS | NS | NS | NS | ZO |
| PS | ZO | ZO | ZO | ZO | ZO | ZO | ZO |
| PM | PB | PS | PS | PS | PS | PS | PB |
| PN | PB | PB | PM | PM | PS | PS | PB |
图 4所示为角位移变化曲线图. 滑模控制能够快速进入稳态,几乎没有超调. 常规PI控制有较大超调,进入稳态所需时间较长. 模糊PI相对PI控制器有较小超调,进入稳态所需时间仍然较长. 图 5为柔性梁振动曲线图. 从图中可以看出滑模控制能够快速抑制柔性梁的振动,抑制效果优于模糊PI和PI控制器. 模糊PI的抑制振动效果也
 |
| 图 4 角位移曲线图Fig. 4 The curve of angular displacement |
 |
| 图 5 柔性梁振动曲线图Fig. 5 The vibration curve of flexible beam |
优于PI控制. 图 6为特征参数辨识曲线图. 由图可知,采用梯度法对特征参数进行辨识,受系统干扰影响较小,参数变化较为平滑.
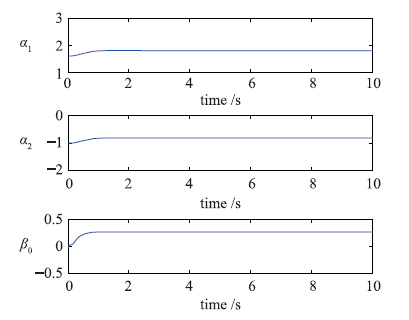 |
| 图 6 特征参数辨识曲线图Fig. 6 The identification curve of characteristic parameter |
图 7是控制器控制量输出变化曲线图. 对滑模控制器输出进行限幅,不超过10.5. 从图中可以看出,滑模控制控制量相比PI控制量、 模糊PI控制量更为平稳.
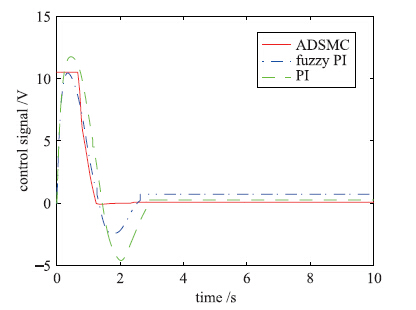 |
| 图 7 控制量输出曲线图Fig. 7 The curve of control output |
本文针对刚柔耦合系统建模较为复杂且所建模型阶次较高的问题,引入特征建模的思想. 在此基础上,提出一种基于PID滑模面的离散自适应滑模控制,实现中心刚体的快速转动,同时快速抑制柔性梁的振动. 该滑模控制器结构简单,易于在线简单实现. 实验表明该滑模控制器具有较好的实用性、 有效性和优越性.
| [1] | 蔡国平,李琳,洪嘉振. 中心刚体—柔性梁系统的最优跟踪控制[J]. 力学学报,2006,38(1): 97-105. Cai G P,Li L,Hong J Z. Optimal tracking control of a flexible hub-beam system[J]. Chinese Journal of Theoretical and Applied Mechanics,2006,38(1): 97-105. |
| [2] | Van Alste J A,Schilden T S. Removal of baseline wander and power line interference from the ECG by an efficient FIR filter with reduced number of taps[J]. IEEE Transactions on Biomed,1985,32(12): 1052-1060. |
| [3] | 洪嘉振,尤超蓝. 刚柔耦合系统动力学研究进展[J]. 动力学与控制学报,2004,2(2): 1-6. Hong J Z,You C L. Advances in dynamics of rigid-flexible coupling system[J]. Journal of Dynamics and Control,2004,2(2): 1-6. |
| [4] | 蔡国平,滕悠优,洪嘉振. 中心刚体—柔性梁系统的旋转运动控制[J]. 宇航学报,2005,26(4): 487-490,494. Cai G P,Teng Y Y,Hong J Z. Active control of rotation motion of a flexible hub-beam system[J]. Journal of Astronautics,2005,26(4): 487-490,494. |
| [5] | 吴宏鑫,胡军,解永春. 基于特征模型的智能自适应控制[M]. 北京: 中国科学技术出版社,2009. Wu H X,Hu J,Xie Y C. Characteristic model-based intelligent adaptive control[M]. Beijing: China Science and Technology Press,2009. |
| [6] | 陈炜. 欠驱动平面柔性机械臂动力学分析与控制研究[D]. 北京: 北京工业大学,2006. Chen W. Dynamics analysis and control of underactuated planar flexible manipulator[D]. Beijing: Beijing University of Technology,2006. |
| [7] | Asghar E,Saa M. Minimum-time optimal control of flexible spacecraft for rotational maneuvering[C] //Proceedings of the 2004 IEEE International Conference on Control Applications. Piscataway,NJ,USA: IEEE,2004: 961-966. |
| [8] | Yang Z H,Ma G F. Multi-objective H2/H∞ control designing for flexible spacecraft[C] //Proceedings of the 2nd International Conference on Machine Learning and Cybernetics. Berlin,Germany: Springer,2003: 1039-1043. |
| [9] | Li Z B,Wang Z L. A hybrid control scheme of adaptive and variable structure for flexible spacecraft[J]. Aerospace Science and Technology,2004,8(5): 423-430. |
| [10] | 张国庆,王永,梁青,等. 一类动量交换刚柔耦合系统的鲁棒减振跟踪[J]. 振动与冲击,2007,26(10): 16-18,34. Zhang G Q,Wang Y,Liang Q,et al. Robust vibration-suppressed tracking for a class of momentum-exchanging rigid-flexible coupled system[J]. Journal of Vibration and Shock,2007,26(10): 16-18,34. |
| [11] | 孟斌,吴宏鑫. 线性定常系统特征模型的证明[J]. 中国科学,2007,37(10): 1258-1271. Meng B,Wu H X. The proof of linear time-invariant systems feature model[J]. Science in China,2007,37(10): 1258-1271. |
| [12] | Zhang X G,Sun L Z,Zhao K,et al. Nonlinear speed control for pmsm system using sliding-mode control and disturbance compensation techniques[J]. IEEE Transactions on Power Electronics,2013,28(3): 1358-1364. |
| [13] | Koshkouei A J,Zinober A S I. Sliding mode control of discrete-time systems[J]. Journal of Dynamic Systems,Measurement,and Control,2000,122(4): 793-802. |
| [14] | 王丽娇. 基于特征模型的高阶线性不稳定系统的参数辨识与控制[J]. 空间控制技术与应用,2010,36(5): 25-31. Wang L J. Characteristic model-based identification and control of high-order linear unstable system[J]. Aerospace Control and Application,2010,36(5): 25-31. |
| [15] | 韩志刚. 动态系统预报的一种新方法[J]. 自动化学报,1983,9(3): 161-168. Han Z G. A new method of dynamic system prediction[J]. Acta Automatica Sinica,1983,9(3): 161-168. |
| [16] | 张国琪,吴宏鑫. 基于特征模型的极点配置自校正调节器[C] //第24届中国控制会议. 杭州: 浙江大学出版社,2005: 770-774. Zhang G Q,Wu H X. The characteristic-model based poles assignment self-tuning regulator[C] //The 24th Chinese Control Conference. Hangzhou: Zhejiang University Press,2005: 770-774. |
| [17] | Sarpturk S Z,Kaynak O. On the stability of discrete-time sliding mode control systems[J]. IEEE Transactions on Automatic Control,1987,32(10): 930-932. |
| [18] | 余跃庆,周刚,方道星. 基于模糊PID融合的柔性机械臂振动压电主动控制研究[J]. 中国机械工程,2008,19(15): 1836-1841. Yu Y Q,Zhou G,Fang D X. Active vibration control for flexible piezoelectric manipuiator based on fuzzy-PID fusion control[J]. China Mechanical Engineering,2008,19(15): 1836-1841. |
| [19] | 曹青松,周继惠,黎林,等. 基于模糊自整定PID算法的压电柔性机械臂振动控制研究[J]. 振动与冲击,2010,29(12): 181-186. Cao Q S,Zhou J H,Ni L,et al. Fuzzy self-tuning PID algorithm of piezoelectric vibration control for flexible manipulators[J]. Journal of Vibration and Shock,2010,29(12): 181-186. |



