1 引言
多质量弹性扭转的共轴运动系统是现实应用中的长轴驱动、 罗拉传动、 滚珠丝杠传动,重载全关节型机器人、 风力发电变桨传动等结构的简化模型,具有重要现实意义. 为了研究这种系统的控制,把多质量弹性扭转系统抽象出来,设计了一个如图 1所示的简易的多质量弹性扭转系统.
 |
| 图 1 多质量弹性扭转系统Fig. 1 Multi-mass elastic torsion system |
为了分析多质量弹性扭转系统的特性,需要建立系统的模型. 传统上,建模主要有机理建模和实验建模方法[1]. 机理建模需要对系统的参数和特性有深入的认识和研究,需要测量的参数多,所用的仪器设备多. 而采用系统辨识的方法则只需要测量系统的输入、 输出信号,运用数学工具就能得到系统的大致模型. 齐晓慧等人[2]讨论了使用Matlab系统辨识工具箱的建模方式,他们通过获得对象的I/O数据来进行系统辨识,借助Matlab系统辨识工具箱进行建模. 徐小平等人[3]讨论了经典系统辨识的一些方法及其缺点,并且引出了神经网络、 遗传算法等一些现代的系统辨识方法.
早期,对系统的描述主要采用整数阶模型,然而,随着分数阶系统理论的发展,分数阶系统模型逐渐得到重视. Podlubny[4]、 Ingman[5]、 Torvik[6]等人的研究结果表明,描述那些本身带有分数阶特性的对象时,采用分数阶系统能够更好地揭示对象的动态特性.
Poinot等人[7],在时域中,通过输入、 输出数据研究了分数阶系统的辨识方法. Hartley等人[8]利用连续分布阶的概念,在频域中讨论了分数阶和整数阶系统的辨识. 而Pintelon等人[9]采用频域法来对分数阶系统进行辨识.
为了解决分数阶系统的阶数辨识问题,一些新的优化算法得以利用,如基于随机数的直接搜索辨识、 基于粒子群算法的辨识、 基于遗传算法的辨识方法[10].
粒子群算法(PSO)是一种基于迭代的优化工具,一种基于群体的随机优化技术. 系统初始化为一组随机解,通过迭代搜寻最优值[11]. 这种算法概念简单,容易实现,需要调节的参数少. 因此本文选择粒子群算法作为系统辨识算法,建立合适的分数阶系统模型,然后通过粒子群最优化的方法进行系统辨识,得到系统的分数阶模型.
2 分数阶系统分数阶系统是以分数阶微积分和分数阶微分方程为基础的模型系统. 分数阶微积分指微分、 积分的阶次可以是任意的或者说是分数的,在很多方面应用分数阶微积分的数学模型,可以更准确地描述实际系统的动态响应,提高对于动态系统的设计、 表征和控制的能力[12].
2.1 分数阶微积分定义分数阶微积分有多种定义,如由整数阶微积分直接扩展而来的Cauchy积分公式、 Grunwald-Letnikov分数阶微积分定义、 Riemann-Liouville微积分定义以及Capotu定义等. 其中Capotu分数阶微分定义为
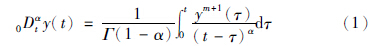
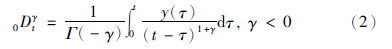
分数阶线性微分方程的一般形式为
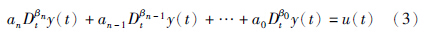
当y(t)具有零初始条件时,可对式(3)进行拉普拉斯变换,得到:
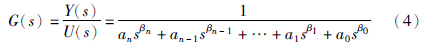
粒子群算法是一种群体智能的优化算法,算法中的每一个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值. 粒子的速度决定了粒子移动的方向和距离,速度随自身及其它粒子的移动经验进行动态调整,从而实现个体在可解空间中的寻优.
假设在一个D维的搜索空间中,由n个粒子组成的种群X=(X1,X2,…,Xn),其中第i个粒子表示为一个D维的向量Xi=(Xi1,Xi2,…,XiD)T,代表第i个粒子在D维搜索空间中的位置,亦代表问题的一个潜在解. 根据目标函数即可计算出每个粒子位置Xi对应的适应度值.
基于粒子群算法的函数极值寻优算法流程图如图 2所示.
 |
| 图 2 粒子群优化算法流程Fig. 2 Flow chart of particle swarm optimization algorithm |
利用PSO算法来进行系统模型的参数整定,其本质是基于一定目标函数的参数寻优问题. 目标函数即适应度函数,对于多质量弹性扭转系统的系统辨识,采用一种常用的时间乘以误差绝对值积分(ITAE准则)作为其目标函数,即:
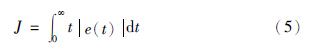
3.2 基于粒子群算法的系统辨识算法
采用时域辨识法,这种方法算法简单,容易用计算机编程实现,得到的结果比较直观. 该方法的主要思想是把系统的传递函数经过拉普拉斯逆变换变成相应的微分方程,解这个微分方程,得到系统的输出函数,将输出函数与测得数据进行比较,借助粒子群算法的寻优能力,整定出输出函数中的待定系数,从而得到系统的传递函数,完成系统辨识.
给定线性微分方程:

给定一个已知系统:
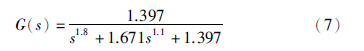
| 整数阶模型阶数 | 待辨识模型结构 | 性能指标J |
| 1阶 |  | 2.6423 |
| 2阶 | 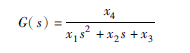 | 1.35 |
| 3阶 | 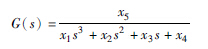 | 3.3344 |
| 4阶 | 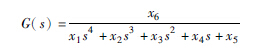 | 1.7230 |
| 5阶 | 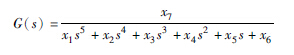 | 35.6482 |
| 6阶 | 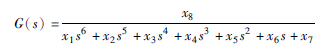 | 745.1802 |
从表 1可以看出,2阶模型结构辨识效果较好,并且2阶模型结构相对简单,因此选择2阶模型结构作为待辨识模型,即待辨识模型为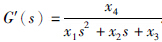 . 这样,就得到了相应的参数整定结果x1=2.4761,x2=2.6773,x3=2.0831,x4=2.0987,J=1.35,辨识后的系统模型为
. 这样,就得到了相应的参数整定结果x1=2.4761,x2=2.6773,x3=2.0831,x4=2.0987,J=1.35,辨识后的系统模型为
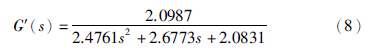
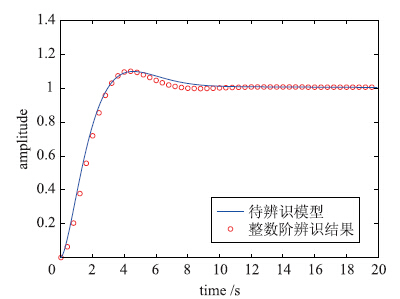 |
| 图 3 验证模型和整数阶辨识结果Fig. 3 The verification model and its integral order identification result |
同样地,对于分数阶模型辨识,设置迭代次数为200次,粒子种群数为30. 采用和整数阶相同的方法,首先给定1阶到6阶的分数阶系统模型结构,将这些模型分别作为待辨识模型进行辨识,根据性能指标J的值,确定一个较为合适的模型以及相应的辨识结果,1阶到6阶分数阶待辨识模型结构以及辨识结果如表 2.
| 分数阶模型阶数 | 待辨识模型结构 | 性能指标J |
| 1阶 |  | 0.6656 |
| 2阶 | 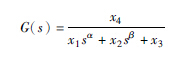 | 0.0146 |
| 3阶 | 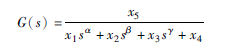 | 0.0983 |
| 4阶 | 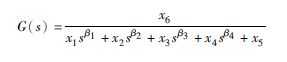 | 0.0742 |
| 5阶 | 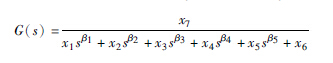 | 1.6040 |
| 6阶 | 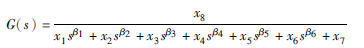 | 1.7309 |
从表 2中可以看出,与整数阶模型结构类似,当选择待辨识模型结构为2阶时,系统辨识的结果较好,因此,令待辨识模型结构为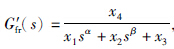 ,其中α、 β为未知阶数. 同样的,得到了相应的参数整定结果x1=1.701 2,x2=2.701 0,x3=2.305 7,x4=2.306 4,α=1.782 5,β=1.093 5,J=0.014 6,即辨识后的系统模型为
,其中α、 β为未知阶数. 同样的,得到了相应的参数整定结果x1=1.701 2,x2=2.701 0,x3=2.305 7,x4=2.306 4,α=1.782 5,β=1.093 5,J=0.014 6,即辨识后的系统模型为
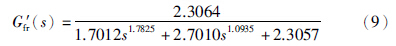
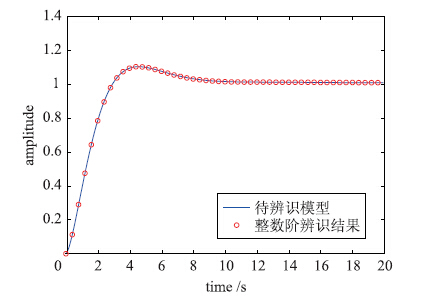 |
| 图 4 验证模型和分数阶辨识结果Fig. 4 The verification model and its fractional order identification result |
根据整数阶和分数阶系统辨识的结果,与待辨识模型进行比较,分别得出其误差如图 5所示.
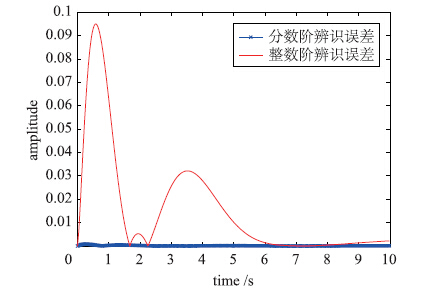 |
| 图 5 整数阶辨识误差和分数阶辨识误差Fig. 5 The error of integral and fractional order identification results |
从图 5中可以看出,对于式(7)这样的分数阶系统,基于粒子群算法的系统辨识能够较好地得到系统的模型,同时,分数阶辨识得到的结果,其误差小于整数阶辨识结果.
4 基于粒子群算法的多质量弹性扭转系统模型辨识 4.1 多质量弹性扭转系统在如图 1所示的多质量弹性扭转系统中,包含有机械部分和PLC(programmable logic controller)控制部分. 机械部分包括: 两块大小不一的圆柱形质量体,分别通过中心轴固定在U型底座上,保证其中心轴线在一条水平线上. 质量体从左数起,第一块质量体的左端通过联轴器与直流电机连接,电机转动驱动第一块质量体转动,然后通过弹簧轴带动第二块质量体转动,第二块质量体右端连接编码器,用于检测第二块质量体的转速,即多质量弹性扭转系统的输出. PLC控制部分包括: CPU模块、 电机驱动模块和计数器模块.
4.2 系统输入输出选择实验建模的方法,将该系统当成一个黑箱系统,通过测量得到输入、 输出信号. 首先,在开环下设定输入信号为2700 °/s的阶跃信号,通过采集第2个质量块的角速度信号,构成输入、 输出信号. 通过数据采集系统所得到的输入、 输出信号如图 6所示.
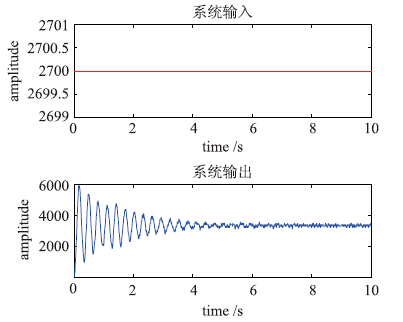 |
| 图 6 系统的输入和输出信号Fig. 6 The input and output signals of the system |
对于整数阶系统辨识,先选取合适的待辨识模型结构,在模型中给定系统阶数. 经过模型结构的确定,选取待辨识的模型G(s)为一个2阶系统:
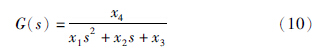

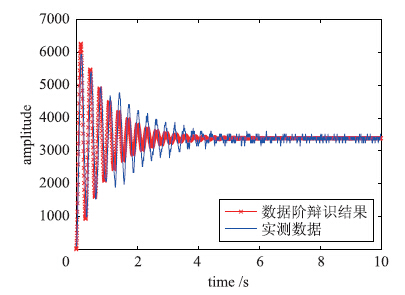 |
| 图 7 弹性扭转系统的整数阶辨识结果Fig. 7 The integral order identification result of the elastic torsion system |
选择合适的待辨识模型结构,其中阶数未知. 经过模型结构的确定,选取待辨识的模型Gfr(s)为
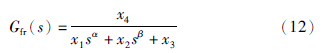
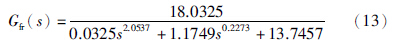
 |
| 图 8 弹性扭转系统的分数阶辨识结果Fig. 8 The fractional order identification result of the elastic torsion system |
基于PSO优化算法的多质量弹性扭转系统的模型辨识,通过解出系统传递函数对应微分方程的数值解,然后利用PSO算法与测得数据进行对比迭代,得到一组合适的参数,从而确定系统模型. 这种方法的算法简单,便于用计算机实现,而且在选取的模型结构合理的情况下,得到的模型能够较好地反映出系统的特性. 同时,从辨识结果可以看出,用分数阶微分方程描述多质量弹性扭转系统比用整数阶微分方程描述更接近于实际.
| [1] | 张晓华. 系统建模与仿真[M]. 北京: 清华大学出版社,2006. Zhang X H. System modelling and simulation[M]. Beijing: Tsinghua University Press,2006. |
| [2] | 齐晓慧,田庆民,董海瑞. 基于Matlab系统辨识工具箱的系统建模[J]. 软件开发与应用,2006,25(1): 88-90. Qi X H,Tian Q M,Dong H R. System modeling based on system identification toolbox in Matlab[J]. Exploitation and Application of Software,2006,25(1): 88-90. |
| [3] | 徐小平,王峰,胡钢. 系统辨识研究的现状[J]. 现代电子技术,2007,15(1): 112-116. Xu X P,Wang F,Hu G. A survey on system identification[J]. Modern Electronics Technique,2007,15(1): 112-116. |
| [4] | Podlubny I. Fractional-order systems and PIλDμ controllers[J]. IEEE Transactions on Automatic Control,1999,44(1): 208-214. |
| [5] | Ingman D,Suzdalnitsky J. Application of dynamic fractional differentiations to the study of oscillating viscoelastic medium with cylindrical cavity[J]. ASME Journal of Vibration and Acoustics,2002,124(75): 642-645. |
| [6] | Torvik P J,Bagley R L. On the appearance of the fractional derivative in the behavior of real materials[J]. ASME Journal of Applied Mechanics,1984,51(4): 294-298. |
| [7] | Poinot T,Trigeassou J C. Identification of fractional systems using an output-error technique[J]. Nonlinear Dynamics,2004,38(1/2): 133-154. |
| [8] | Hartley T T,Lorenzo C F. Fractional-order system identification based on continuous order-distributions [J]. Signal Process,2003,83(11): 2287-2300. |
| [9] | Pintelon R,Guillaume P,Rolain Y,et al. Parametric identification of transfer functions in the frequency domain: A survey[J]. IEEE Transactions on Automatic Control,1994,39(11): 2245-2259. |
| [10] | 余志雄. 分数阶系统辨识与控制研究[D]. 北京: 北京化工大学,2009. Yu Z X. Studied on identification and control of fractional order system[D]. Beijing: Beijing University of Chemical Technology,2009. |
| [11] | 刘建华. 粒子群算法的基本理论及其改进研究[D]. 长沙: 中南大学,2009. Liu J H. The research of basic theory and improvement on particle swarm optimization[D]. Changsha: Central South University,2009. |
| [12] | 赵春娜,李英顺,陆涛. 分数阶系统分析与设计[M]. 北京: 国防工业出版社,2011.Zhao C N,Li Y S,Lu T. Analysis and design of fractional order system[M]. Beijing: National Defense Industry Press,2011. |
| [13] | 薛定宇,陈阳泉. 高等应用数学问题的MATLAB求解[M]. 第2版. 北京: 清华大学出版社,2008. Xue D Y,Chen Y Q. Advanced applied mathematical problem solutions with Matlab[M]. 2nd ed. Beijing: Tsinghua University Press,2008. |



