1 引言
现代社会依赖于复杂关键基础设施所提供的能源、 交通、 食物、 医疗护理、 应急响应及物理和网络安全等. 计算机、 自动控制和信息技术的发展增强了基础设施运行过程的效率,但更大效能的需求进一步增加了系统中智能传感器、 控制结构和方法的综合,意味着控制系统的复杂网状连接和相互依赖. 而近年来大型复杂基础系统由系统失控、 自然灾害、 恐怖袭击等所导致的失效增加,引起了巨大的经济损失和安全隐患,如切尔诺贝利核电站事故、 挑战者号航天飞机爆炸、 尤马停电及最近的福岛地震和海啸引发的核反应堆事故等. 为了减小这些事件造成的严重后果所带来的影响,其控制系统的结构和算法需要将人和控制装置所集成系统的“弹性”最大化[1, 2]. 系统具有“弹性”意味着系统在遭到破坏之后最终能恢复正常工作状态或是性能稍有退化下的一定安全等级的运行; 弹性与脆性相对,指系统具有一定的韧性; 脆性指控制系统非常敏感,破坏会导致其毁灭性灾难[3, 4] .
弹性控制(resilient control)是近几年随着计算机化和数字控制系统发展起来的新的研究方向,主要针对以运行效率和稳定性为目标的关键基础设施的监测与控制,这些系统具有多功能性和可靠性,但其复杂网状结构和人机交互中存在不利的环境和不确定性,为控制系统设计增加了额外的参数要求; 设计过程中的主要目标是在状态已知的基础上采取措施来确保系统安全. 与传统控制不同,弹性控制中的状态包含了维持控制最终目标所需的信息,强调在恶性和不确定环境下控制系统的设计[5, 6],且更侧重于复杂控制系统自身独特的相互依赖关系.
目前国内还没有关于弹性控制的系统完整的公开出版物,相对于现有控制理论,弹性控制具有相对独特的机制,本文将对弹性控制概念、 特性、 结构、 代表算法、 性能量化及发展应用的研究作以总结、 评述和展望.
2 弹性控制的概念 2.1 弹性控制的定义弹性控制是指系统能够忍受系统结构和设计参数、 控制装置结构和参数引起的波动[7],即在异常情况下(包含恶意和灾难性威胁下)系统维持状态已知和可以接受的一定恢复程度的正常运行. 威胁包括与正常情况相悖的和使控制系统不稳定的因素,如人为误差、 恶意人为攻击、 复杂的潜在因素和相关性等[8]. 弹性控制系统设计和运行的目的是使不良事件的发生概率最小化; 大部分已发生的不良事件能够得到缓解; 如果某些不良事件不能被完全缓解,也可最小化其负面影响; 在短时间内系统能够恢复至正常运行[9].
弹性控制中的“弹性”强调对变化和人为、 恐怖主义的和自然的灾害能够迅速适应、 迅速恢复和最小化其影响. 主要包含3个因素: 1) 抵制干扰影响、 保持系统参数在某安全范围的能力; 2) 遇到干扰时局部失效,而不是灾难性的破坏; 3) 干扰过后容易恢复.
弹性控制主要有2个研究领域: 状态认知和弹性设计. 状态认知是获取正常系统遭受威胁的相关信息,是在原始数据的基础上进行信息的智能融合、 集中和优化,维持控制系统正常工作; 弹性设计在可接受程度风险下维持系统正常运行,将冗余技术用于控制系统可靠性设计. 弹性控制系统具体结构框图如图 1所示[10].
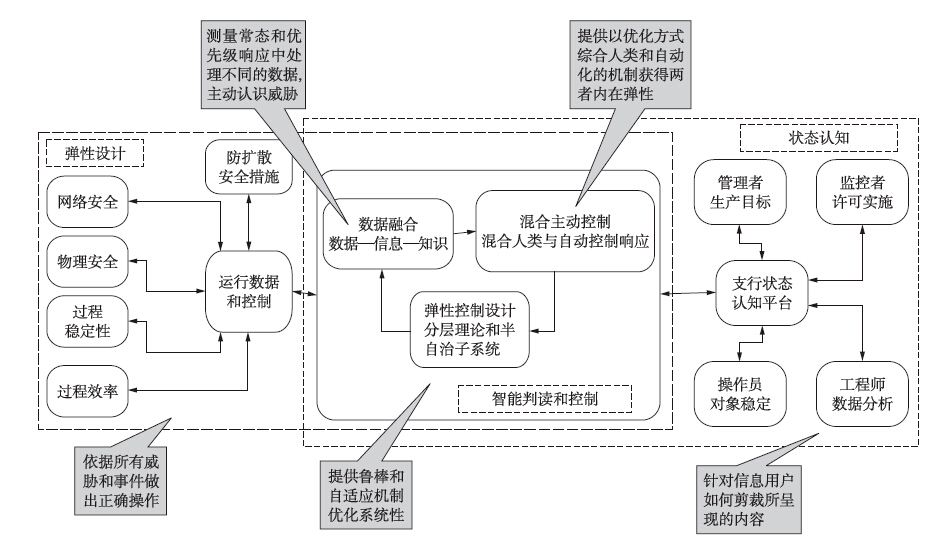 |
| 图 1 弹性控制系统结构框图Fig. 1 Structure diagram of resilient control system |
为减小异常情况的影响,弹性控制系统必须减少不良事件发生的可能性,具有预测、 适应、 感知和回应的能力,这些能力越强,控制系统抗干扰能力也就越强. 控制系统可通过增强这4个方面来提高系统性能[11, 12].
1) 预测性. 弹性控制系统必须能够预测干扰和威胁. 通过主动而非被动的反应预知来使给定系统具有预测能力,许多模拟和数控系统对于参数变化的响应由反馈或反应控制以回放的形式呈现数据. 弹性控制系统可以通过计算期望的系统或集成系统的响应提出控制动作、 计划,并向操作人员指明预期的、 可接受的响应限制,在操作人员允许后引导控制操作,并进一步指示系统的反应,确保对象的响应与预期一致.
2) 认知性. 弹性控制系统必须具有认知设备状态和系统威胁的能力. 给定的弹性控制系统具有认知的能力,有助于系统获得目前状况的正确信息和知识. 控制系统从传感器输入需认知系统中设备和整体运行状态,包含
与期望运行结果的偏差,由此决定输入是否与感知到的设备或系统状态或期望运行相一致,这有助于识别干扰和控制.
3) 反应性. 弹性控制系统必须能够对感知情况做出精确和快速反应. 当系统状态已知,必须理解状态的意义并能够提供相应的动作. 弹性控制系统依据输入传感器值进行响应,判断此值是否精确、 响应是否恰当,并警示操作人员设备和系统响应的运行是否正常.
4) 适应性. 弹性控制系统必须能够按期望进行响应,这一能力称为适应性; 包括根据预期和非预期的干扰调整控制过程和输出信号. 适应性是系统从最大状态到最小可接受程度运行的缓冲能力. 并非所有的事件都是可预测的,缓冲对于突发事件是有利的,可为最小系统在期望或意外事件中维持运行提供强化机制,如当系统偏离期望响应时可警告操作员或调整控制函数(如增益),使系统自适应响应,确保系统继续可接受的运行.
3 与现有控制技术的区别和联系 3.1 弹性控制与鲁棒控制的区别鲁棒控制是系统在外界和内部干扰(激励和突变)作用下改变结构和元件维持某些性能的特性[13]. 而弹性控制是指系统在遇到意想不到的极端干扰和罕见干扰的情况下,能够通过快速改变结构和参数,适当地降低其功能,同时一旦干扰停止能够迅速恢复.
鲁棒性和弹性并不是系统的通用特性,而是与某一类特定干扰相关[14]. 控制系统对于某一类干扰具有鲁棒性和弹性,而对另外一类干扰呈现脆性. 如集中控制系统的鲁棒性比分散系统强,而弹性则相反. 具有全局协调能力的系统能够经受更大范围的不确定性或干扰,但对不可预见的攻击和故障可能失效. 故在设计系统结构和控制方式时鲁棒性和弹性的折中必不可少. 另外,鲁棒控制是系统提前预知的特性,设计者在最初就已将其考虑在规划中,通过增强系统的冗余而获得; 而弹性控制有突现特性,设计过程未知,需要随环境变化的灵活性.
3.2 弹性控制与智能控制的区别智能控制是针对控制对象及其环境、 控制目标和任务的不确定性和复杂性而提出. 智能控制可以自动测量被控对象的被控制量,并求出与期望值的偏差,同时采集输入环境的信息,进而根据所采集的输入信息和已有知识进行推理,得到对被控对象的输出控制,同时使偏差尽可能减小或消除. 一般使用人工智能控制方法,如神经网络、 模糊逻辑、 机器学习、 进化计算和遗传算法等,无需建立被控对象的数学模型,特别适合非线性对象、 时变对象和复杂不确定的控制对象. 智能控制系统具有分层递阶控制组织结构,便于处理大量的信息和储存的知识,并进行推理; 也具有自适应能力和鲁棒性; 还可以对未知特性的固有信息进行学习,并将得到的经验用于进一步的估计、 决策和控制,使系统的性能得到改善.
而弹性控制只是指在系统遇到意想不到的极端和罕见的干扰时所具有的调节和恢复能力,不具有智能控制的学习能力; 在系统正常运行或只有一般干扰情况下,弹性控制并不起到突出作用,系统所呈现的是通常控制所具有的特性和能力. 所以弹性控制和智能控制可以进行融合,系统可以具有智能弹性控制的综合特性.
3.3 弹性控制与最优控制的区别最优控制是现代控制理论的一个主要分支,研究的主要问题是: 在满足一定约束条件下,寻求最优控制策略,使性能指标取极大值或极小值. 针对一个受控的动力学系统或运动过程,从一类允许的控制方案中找出一个最优的控制方案,使系统的运动在由某个初始状态转移到指定的目标状态的同时其性能指标值为最优[15, 16].
而弹性控制并不侧重于某一个或某些指标的最优,而是通过各个指标之间的折中,强调系统间的协同关系,增强系统在异常情况下的恢复能力,提高其应对各种程度干扰和威胁的能力; 异常情况消除后系统性能恢复到可接受程度而非最优.
3.4 弹性控制与容错控制、 可重构控制的区别容错控制指控制系统在传感器、 执行器或元部件发生故障时,闭环系统仍然能够保持稳定,并且能够满足一定的性能指标. 容错控制具有使系统的反馈对故障不敏感的作用,分为被动容错控制和主动容错控制; 前者利用鲁棒控制技术使系统对某些确定的故障具有不敏感性,不需要故障诊断和控制重组,具有固定形式的控制器结构和参数; 后者对发生的故障主动处理,利用获知的各种故障信息重新调整控制器参数,甚至改变控制器结构. 但容错控制与重构控制在系统面临威胁(风险)时没有提供维持性能的全局计划[17, 18],没有关于在状态认知基础上控制行为和故障检测、 诊断相关联的研究; 仅能包容但并不考虑恶意动作破坏正常的系统行为,缺少对所获得信息的更高水平的分层次融合、 优化,不能确保状态已知和优化响应; 也没有全面考虑与系统相关的计算机环境中的故障.
弹性控制综合系统网络和物理结构设计和运行,因此克服了计算可靠性和故障容错控制的限制. 具有更强的处理意外事件的能力,以比传统控制更加灵活的方式确保系统安全,定量评估、 测量和判别是主要难点问题. 很多弹性控制中包含了社会和人为因素,自动化和人类任务互相影响,为彼此提供冗余度,为安全问题提供了保障.
3.5 弹性控制与自适应控制的区别自适应控制是一种对系统参数的变化具有适应能力的控制方法,系统的参数具有较大的不确定性,并可能在系统运行期间发生较大改变. 自适应控制只能忍受某些不确定性,不能有效地提高系统从无法预料的不利条件和紧急情况下恢复的能力[19].
而弹性控制不仅具有对任何程度干扰的抵抗能力,也能保持系统参数在一定程度安全范围内,可呈现“温和”地避免灾难性破坏,并且干扰较小时系统易于恢复[20].
因此,现有控制理论对于意外、 极端和罕见干扰的调节和恢复能力的局限性表明了其与弹性控制的区别及研究的必要性[21].
4 弹性控制的性能量化弹性控制系统遇到不良事件时能够提供和维持可接受程度的性能和功能,其性能可以通过以下2个方面进行衡量[22, 23]: 1) 静态响应,对于给定事件、 生产和质量方面损失多少性能; 2) 动态响应,事件去除后,系统需要多长时间恢复初始性能.
4.1 弹性控制过程性能变化根据弹性控制概念和性质,弹性控制过程的性能变化如图 2所示.
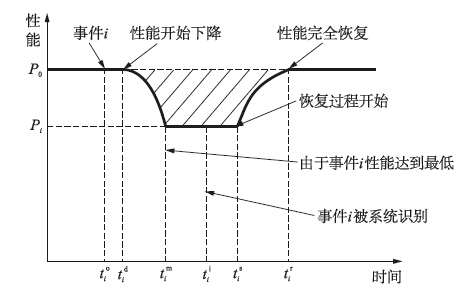 |
| 图 2 弹性控制性能变化Fig. 2 Performance changes of resilient control |
图 2中,toi为事件i发生时间,tdi为系统性能开始衰退时间,tmi为系统性能由于事件i影响到达性能最低点的时间; tii为事件i被系统或操作人员辨识的时间; tsi为系统由操作人员手动或控制系统自动恢复的起始时间;tri为系统从事件i中完全恢复的时间; P0为事件i发生时的初始性能; Pi为系统由事件i引起的最低性能.
4.2 弹性指数Zhu等[7, 14, 22]对于性能指标做了初步研究,以弹性指数来衡量系统的弹性. 弹性指数(resiliency index,RI)定义为
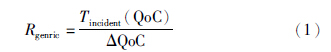
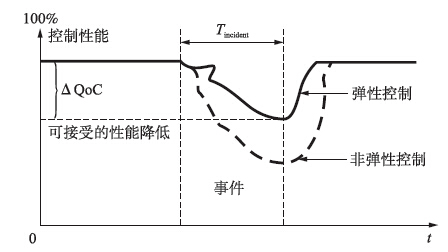 |
| 图 3 弹性指数示意图Fig. 3 Schematic diagram of resiliency index |
由于弹性控制的复杂性和灵活性,针对不同的应用领域和控制对象有不同的具体控制结构[24]. 本文总结了几种具有代表性的结构.
1) 弹性工业控制结构.图 4为生产线或工程系统的3层弹性控制结构. 图中人员层位于结构顶端,操作人员直接通过传感器或人机界面监测过程数据,通过直接操作执行机构或输入命令控制过程; 过程层在结构最下层,物理或化学过程由传感器监测、 执行机构控制; 控制层位于中间,通过传感器收集控制过程实时数据,由人机界面提供状态和诊断数据,接受操作人员命令和设定,由执行机构控制被控过程[7].
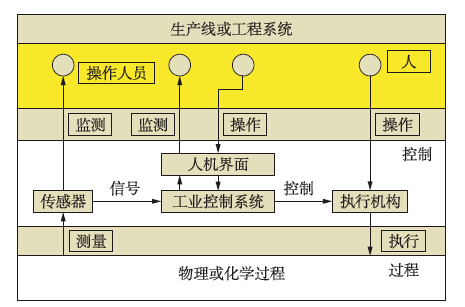 |
| 图 4 弹性工业控制结构Fig. 4 Structure diagram of resilient industrial control |
2) 弹性车辆控制结构.图 5中车辆在敌对环境中遭受多个不同攻击,控制效率虽有所下降但仍能维持一定程度的控制效果. 图中综合了控件级别的防御和代码级别的防御,前者指在控制系统设计阶段考虑执行机构、 传感器、 网络等受到的攻击对于控制器的影响,采用闭环冗余技术检测和感知攻击,利用弹性估计器辨识攻击,由控制器提供缓解策略; 后者指在系统开发阶段采用代码防御技术预防恶意代码注入控制器操作系统[25].
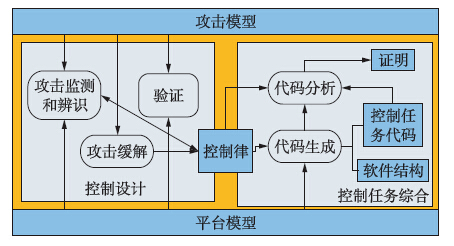 |
| 图 5 弹性车辆控制结构Fig. 5 Structure diagram of vehicle resilient control |
3) 弹性网络控制结构.图 6是网络和服务弹性的核心弹性控制环,高度抽象后被控系统由网络机制和服务机制组成,来实施整个系统的希望特性. 网络机制是路由或拥堵机制,需要网络中数据包有弹性转发,服务机制依赖于提供给用户的服务种类,如视频直播和网络登录. 控制系统由于保护措施最初呈现足够的弹性抵抗挑战,这些措施在设计整个系统阶段已定义. 提供给用户的服务由测量元件检测,它提供服务方式的信息和内回路的状态,并计算弹性状态与弹性目标比较; 存在偏差时由修复元件提供恰当的动作,使控制系统到达希望的状态,完成恢复过程,继续以合适的方式为用户服务.
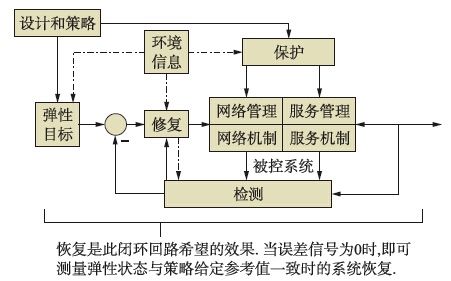 |
| 图 6 弹性网络的控制环结构Fig. 6 Control loop structure of resilient network |
4) 弹性航空推进系统控制结构.传统航空发动机控制结构中,控制器接受飞行控制传输的指令,计算当前飞行状态下适当的控制量,控制发动机安全可靠运行. 图 7中在传统发动机控制系统结构中增加了风险管理和控制模式选择子系统、 发动机寿命和运行诊断子系统、 发动机监视子系统等,在飞行控制部分增加了飞行风险管理子系统[26, 27]. 这些子系统主要用于评估紧急事件等级、 飞机和发动机运行状态及应急控制可能会给发动机安全运行带来的风险,从而在风险和性能之间进行折中,为飞机和航空发动机提供一定的额外性能.
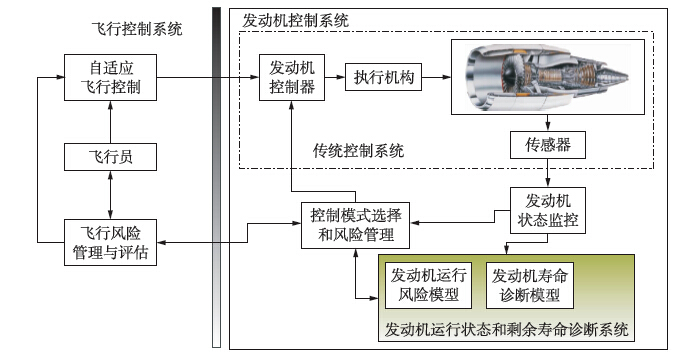 |
| 图 7 弹性航空推进系统控制结构Fig. 7 Control structure of resilient propulsion system |
目前弹性控制算法处于起步阶段,根据其研究目标可分为4类: (1) 以解决控制系统模型、 控制器等单个或多重不确定性为目标的弹性控制算法[28, 29]; (2) 传感器、 测量结果存在干扰的弹性算法[22]; (3) 以协调整个系统组成为基础的弹性控制算法[26, 27]; (4) 以现存控制算法为基础,结合弹性控制选择机制,综合多种控制算法优点的综合弹性控制算法[30, 31]. 本文重点介绍第2类和第4类算法.
(1) 传感器存在干扰时模型预测输出的弹性控制算法
假设被控对象数学模型为
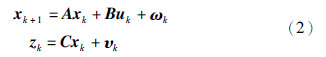
1) 传感器数据过滤
在卡尔曼滤波的基础上,预测式(2)表示系统状态和误差协方差为
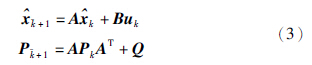
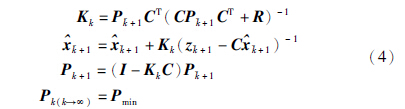
卡尔曼滤波本质上是一组数学公式,是进行预测校正类型估计器,估计误差协方差、 产生期望系统状态的最优估计.
2) 传感器数据预测
如果传感器测量值zk+1由于射频干扰导致的链接失效而丢失,则预测的传感器数据如式(5)所示. 算法时序如式(6)所示,用于确保及时传递传感器数据:
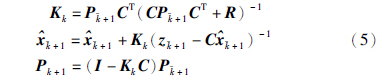
基于模型预测的弹性控制算法中新的传感器信号经滤波后传递到控制器,如果在时间阈值内没有新的传感器数据,算法将提供预测的传感器数据和表示预测程度的更新置信水平到控制器. 如果新的传感器数据zk+1在时间阈值后到达,但在下一个采样时间结束之前,则仍用于更新当前预测值,如式(6)所示.
如果新的值在下一个采样之后到达,则认为丢失. 基本思想为因为新数据能够更精确反映控制器的真实情况,因此丢弃旧数据. 算法中传感器数据包延迟和丢失以统一的方式处理. 如果由于链接失效连续的传感器测量值丢失,则相应的传感器连续预测值为
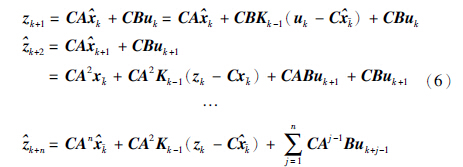
3) 风险估计和预警机制
数据置信度和控制品质一起定义. 其定义为: 控制过程输出值和设定值之差小于一定输出误差允许值a的概率:
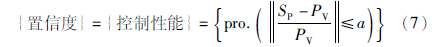
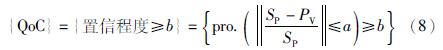
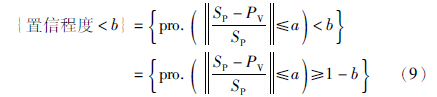
置信度表示预测结果的好坏,并由式(8)提供实时控制性能信息. 当置信度低于式(7)中的阈值时,形成警报告知用户. 这种控制性能连续更新信息或警报传送至人机界面,信息也可用于控制律设计,进一步提高控制性能; 此方法中控制器设计可以与弹性算法独立设计,此弹性算法可为已有控制器提供连续传感器数据流. 由此可见,此算法可以用于忍受短时链接失效,以避免系统关闭引起的高昂代价.
(2) 综合μ算法和L1自适应的综合弹性控制算法
鲁棒控制目的在于减小对象对外部干扰和内部故障的敏感性并确保一定的性能,弹性控制通过实时改变运行包线提高对象从意外的不利条件、 故障和紧急情况中恢复的能力. 鲁棒μ算法[32]针对包含模型不确定性因子和干扰噪声的鲁棒控制有良好的动态性能和鲁棒性能. 弹性飞行控制的L1自适应算法具有快速自适应和同时跟踪一致有界的输入、 输出信号的作用[33, 34],既具有鲁棒性也有自适应性,可以作为弹性控制器,闭环L1自适应控制器结构如图 8所示[30].
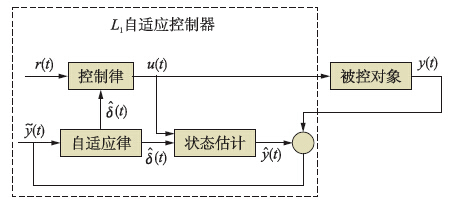 |
| 图 8 控制器闭环控制结构Fig. 8 Closed-loop control structure of the controller |
在图 8的基础上,利用有限状态机[35]进行离散决策,采用故障检测器检测对象状态,采用无扰转换器控制鲁棒和弹性控制器间的转换,以此构成鲁棒和弹性综合控制,如图 9所示. 其中弹性L1自适应算法和鲁棒μ综合算法具体形式可参阅相关文献[34, 35, 36, 37]. 图 9中的有限状态机是一个5维向量[Q,Σ,δ,q0,F],其中Q={q1,q2}为有限集合,表示状态; Σ表示状态标识,有2个状态标志,分别为{0,1},0表示正常状态,1表示异常状态; δ: Q×Σ→Q为状态转移函数; q0为初始状态; F∈Q是可接受状态或最终状态. 当系统中出现异常状态,状态标识由0变为1,同时有限状态机使状态量从正常状态q1转换为异常状态q2,系统采取相应措施确保系统安全工作,并保持在q2; 当系统恢复正常状态,标志变为0,状态返回q1. 弹性控制的作用在于使状态q1和q2间的转换快速、 安全,确保系统从意外的不利条件、 故障及紧急状态中恢复. 图中滤波器组确保系统在鲁棒和弹性控制切换过程中不发生突变,其输出作用于控制器减缓控制器输出; 控制作用总输出为
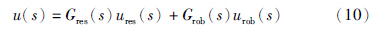
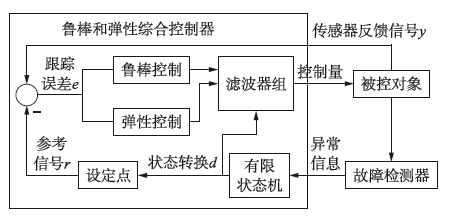 |
| 图 9 鲁棒和弹性综合控制框图Fig. 9 Block diagram of the robust and resilient integrated control |
弹性的概念始于社会生态学和心理学,上世纪70年代,加拿大生态学家Holling为描述生态系统中效率和持续、 恒定和变化、 可预测和不可预测之间的折中,第1次完整地描述了这一概念[36]; 弹性用来衡量系统可持续性和承受变化的干扰、 维持种群关系的能力. 1982年Werner第1次在心理学领域运用了此概念,他指出弹性是儿童从创伤期和病危期恢复的能力[37]. 此后,弹性概念被Holling进一步完善. 1986年,他将弹性重新定义为: 系统在干扰下维持自身结构和行为模式的能力[38]. 1995年,他在前2个定义的基础上,将弹性概念再次定义为: 系统缓冲的能力或吸收扰动的能力,或系统在由控制参数和过程变化改变其结构前干扰被吸收的幅值[39].
1984年,Pimm在Holling工作的基础上,将弹性定义为: 衡量系统在干扰作用下恢复到平衡点的速度[40]. 而Holling本人认为这是衡量“工程弹性”的稳定性,他此前的定义是衡量“生态弹性”的吸收能力. 自此弹性开始具有工程领域的定义,由生物和生态领域进入复杂系统应用及控制[41, 42].
2006年英国科学家Hollnagel、 Woods出版著作《Resilience Engineering: Concepts and Precepts》总结了弹性工程概念和原理,标志着弹性工程领域应用的完善. 此后,2008年开始召开了第1次弹性控制国际会议,至今已举行7届,已有越来越多的研究工作者对此产生兴趣[43, 44]. 2009年Rieger完整提出了弹性控制系统的概念,强调针对敌对的和不确定的环境设计控制系统,并指出弹性控制系统将成为下一代控制领域研究的主要方向[10]. 此后,弹性控制理论由最初的分析弹性设计的重要性和弹性控制的概念、 研究内容,逐步深入,已开展了弹性控制算法和指标定性分析等方面的研究; 同时弹性控制应用的领域也逐步扩大.
最近,弹性用于实体如公司、 社区、 政府等提高其应对灾难性事件(如自然灾害、 恐怖袭击)和从中迅速恢复的能力[45]; 特别是在监控关键基础设施方面有新的发展[44]. Serugendo等基于元数据弹性策略设计计算机系统,可采用动态行为适应可预测的突发事件[46]. Villez等给出关于集成不同故障检测和辨识方法、 控制方法获得关键基础设施弹性的基本例子[47]. Mili等给出了电力系统的5种运行状态,给出了在鲁棒性和弹性之间折中的控制结构[48].
弹性在网络方面也得到了研究[49, 50],弹性网络系统在正常操作遇到故障和挑战时仍能提供和维持可接受的服务. Anderson等描述了网络安全方案使网络系统具有更强的鲁棒性、 安全性和弹性[51].
此外,弹性控制在经济、 航空工业[52]、 灾难应对[53]、 核电站[54]和石油、 天然气工业[55]、 加热通风空气调节系统、 电网[56]、 应急健康保健[57]和交通运输工程等领域已得到应用[58, 59]. 核电站由于工作的特殊性,在设计阶段就考虑到安全问题,但仍有无法预测的意外情况发生; Bruno等针对意外事故中产生的大量混乱信息,提出了以认知分析为基础的快速决策机制,为弹性控制提供支持和保证[60]. 弹性飞行控制研究为提高检测、 避免和防止飞行系统失效. 考虑到先进控制和自主能力,Krishnakuma等探索飞机在可能导致失控的非正常条件下自动检测、 减缓和安全恢复的能力; 验证和确认软件为基础的飞行关键系统,进一步深入研究导致飞行不利条件的因素,包含结冰、 结构降质及其发生条件[26]. 所以,弹性控制的作用日益突出,其设计过程需要涉及多技术学科和系统,是一个系统工程; 与传统控制不同,不再是个人独立完成设计过程而是需要不同领域的专家以团队形式共同完成.
7 存在问题及未来研究方向弹性控制是近年来发展起来的、 逐步引起人们研究兴趣的一个现代控制理论分支. 数字控制为远程检测和控制提供了条件,控制系统和设施的复杂度要求增加控制的安全性和可靠性. 同时,网络连接为入侵控制系统提供了方便途径,也增加了控制系统的复杂性. 为更好地理解和优化控制结果,需要用数学方式精确表示这一复杂性. 无论是基础设施还是工业系统都会以一定的代价获取系统一定程度的弹性. 目前弹性控制理论在各领域的应用都有一定的涉及,但仍处于起步阶段,有一些问题需要研究:
1) 研究分析、 测量和监控系统弹性的有效方法. 弹性控制以大量的系统信息为基础,信息的存储、 访问、 修改和转移尤为重要,研究信息结构对控制设计的影响更为重要,尤其是当系统有残缺和延迟测量值时的状态信息及估计; 对于故障和未知参数具有弹性的算法研究; 干扰和攻击下的安全评估和控制系统设计; 解决将模型的不匹配和紧急情况合并入弹性控制结构的问题.
2) 建立事故模型、 风险变化和决策模型. 弹性控制中风险与收益并存,风险模型是系统监控和修正,所建立事故模型和风险模型必须具有代表性,能捕捉系统的复杂功能及所有可能的未来事件,预报短期或长期影响,为控制提供约束和依据.
3) 弹性控制指标的进一步完善和规范. 现有的弹性控制的性能指标仅以弹性指数来进行衡量,而没有与自身控制特征相联系的弹性控制指标,难以从多方面定量衡量系统的弹性,如进一步研究系统在事故去除后从恶性事件中恢复到初始性能的时间指标; 减小或去除系统弹性恢复的延迟大小; 如何从弹性角度量化系统行为; 系统的弹性随时间、 运行状态、 寿命的变化程度等.
4) 融入风险管理. 弹性控制系统主要针对系统恶性事件进行处理,控制策略从原来的反应式控制转变为评估潜在威胁、 采取必要保护措施的主动控制,所以风险估计是减小事故和负面影响的必不可少的步骤; 另外对于已存在系统,需要解决以下问题: 如何提高其弹性,如何从已知实时信息和先进控制算法,利用风险评估最小化系统失效的可能性.
5) 弹性控制系统的实验方法研究. 由于弹性控制的特点,对于系统控制效果的实验研究成为难点之一. 需要具有针对性的实验方法、 步骤,研究系统在不同紧急状况下的实验需求; 同时设计综合仿真平台,探索和验证处理系统实时数据的弹性控制策略; 建立物理实验和仿真实验的协同验证机制.
作为新一代控制系统,弹性控制不仅提高工业、 生态和社会系统的效率和可靠性,同时也监控系统潜在的破坏性和有害事件,多方面描述系统稳定性、 鲁棒性、 生存性、 自适应性、 安全和弹性. 随着弹性控制理论的研究和发展,其必将成为控制领域研究的热点.
| [1] | Hollnagel E. Resilience engineering in a nutshell,resilience engineering perspectives: Remaining sensitive to the possibility of failure[M]. Aldershot,UK: Ashgate Publishing Limited,2008: 1-5. |
| [2] | Umberto P. Resilience and sustainable development: Theory of resilience,systems thinking and adaptive governance[R]. Vienna,Austria: Vienna University of Economics and Business,2012. |
| [3] | Hollnagel E,Woods D D,Leveson N. Resilience engineering: Concepts and precepts[M]. Aldershot,UK: Ashgate Publishing Limited,2006: 6-12. |
| [4] | Naidu S. Control system design session[C] //Proceedings of the 1st International Symposium on Resilient Control Systems. Piscataway,NJ,USA: IEEE,2008. |
| [5] | Ji K,Lu Y,Liao L,et al. Prognostics enabled resilient control for model-based building automation systems[C] //Proceedings of the 12th Conference of International Building Performance Simulation Association. Piscataway,NJ,USA: IEEE,2011: 286-293. |
| [6] | Hollnagel E,Pari'es J,Woods D D,et al. Resilience engineering in practice: A guidebook[M]. Aldershot,UK: Ashgate Publishing Limited,2011: 1-156. |
| [7] | Ji K,Wei D. Resilient industrial control system(RICS): Concepts,formulation,metrics,and insights[C] //Proceedings of the 3rd IEEE International Symposium on Resilient Control Systems. Piscataway,NJ,USA: IEEE,2010: 15-22. |
| [8] | Yang Y G,Sydnor R. Resilient control for critical infrastructures and systems[R]. Rockville,USA: Nuclear Regulatory Commission,2011. |
| [9] | Ji K,Wei D. Resilient control for wireless networked control systems[J]. International Journal of Control,Automation,and Systems,2011,9(2): 285-293. |
| [10] | Rieger C G,Gertman D I,McQueen M A. Resilient control systems: Next generation design research[C] //Proceedings of the 2nd Conference on Human System interactions. Piscataway,NJ,USA: IEEE,2009: 629-633. |
| [11] | Stevens L,Rieger C,Phoenix W. HTGR resilient control system strategy[R]. Idaho Falls,USA: Idaho National Laboratory,2009. |
| [12] | Mitchell S M,Mannan M S. Designing resilient engineered systems[J]. Chemical Engineering Progress,2006,102(4): 39-45. |
| [13] | Fiksel J. Designing resilient,sustainable systems[J]. Environmental Science & Technology,2003,37(23): 5330-5339. |
| [14] | Jin X,Edwards R,Ray A. Integrated robust and resilient control for nuclear power plants[C] //Proceedings of the 6th ANS International Topical Meeting NPIC & HMIT,Paper 3 Session I & C Grid Appropriate Reactor,Knoxville. Piscataway,NJ,USA: IEEE,2009: 807-817. |
| [15] | Cassel,Kevin W. Variational methods with applications in science and engineering[M]. Cambridge,UK: Cambridge University Press,2013. |
| [16] | Lebedev L P,Cloud M J. The calculus of variations and functional analysis with optimal control and applications in mechanics[M]. Singapore: World Scientific Publishing,2003: 99-157. |
| [17] | Strigini L. Fault tolerance and resilience: Meanings,measures and assessment,centre for software reliability[D]. London,UK: City University,2009. |
| [18] | 李江海,黄晓津. 核电数字化控制系统安全综述[J]. 原子能科学技术,2012,46(9): 411-416. Li J H,Huang X J. Control system security in nuclear power plan[J]. Atomic Energy Science and Technology,2012,46(9): 411-416. |
| [19] | Wen J,Liu F. Robust model predictive control for fuzzy systems subject to actuator saturation[C] //Sixth International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway,NJ,USA: IEEE,2009: 400-404. |
| [20] | Jr Santos E. On threats from intelligent adversaries[C] //International Symposium on Resilient Control Systems. Piscataway,NJ,USA: IEEE,2008. |
| [21] | Rieger C,Moore K,Baldwin T. Resilient control systems: A multi-agent dynamic systems perspective[C] //2013 IEEE International Conference on Electro/Information Technology. Piscataway,NJ,USA: IEEE,2013: 1-6. |
| [22] | Zhu Q Y,Wei D. Quantitative methods for resilient control systems[C] //International Symposium on Resilient Control Systems. Piscataway,NJ,USA: IEEE,2013. |
| [23] | Trimintzios P. Measurement frameworks and metrics for resilient networks and services[R]. Heraklion,Greece: European Network and Information Security Agency (ENISA),2010. |
| [24] | Antunes P,Mouro H. Resilient business process management: Framework and services[J]. Expert Systems with Applications,2011,38(2): 1241-1254. |
| [25] | Pajic M,Nicola B,Weimer J,et al. Towards synthesis of platform-aware attack-resilient control systems[C] //Proceedings of the 2nd International Conference on High Confidence Networked Systems. New York,NJ,USA: ACM,2013: 75-76. |
| [26] | Krishnakumar K,Viken S. Integrated resilient aircraft control stability,maneuverability,and safe landing in the presence of adverse conditions[R]. Washington,USA: National Aeronautics and Space Administration,2009. |
| [27] | McGlynn G E,Litt J S,Lemon K A,et al. A risk management architecture for emergency integrated aircraft control[C] //AIAA Infotech@Aerospace Conference. Los Angeles,CA,USA: AIAA,2011: 1-13. |
| [28] | Mahmoud M S. Resilience control of uncertain dynamical systems[M]. Berlin,Germany: Springer-Verlag,2004: 1-233. |
| [29] | 朱淑倩,张承慧,李振波,等. 不确定奇异时滞系统的时滞相关型鲁棒H∞弹性控制[J]. 控制理论与应用,2007,24(4): 587-593. Zhu S Q,Zhang C H,Li Z B,et al. Delay-dependent robust resilient H∞ control for uncertain singular time-delay systems[J]. Control Theory & Applications,2007,24(4): 587-593. |
| [30] | Jin X,Ray A. Integrated robust and resilient control of nuclear power plants for operational safety and high performance[J]. IEEE Transactions on Nuclear Science,2010,57(2): 708-716. |
| [31] | Villez K,Srinivasan B,Rengaswamy R,et al. Resilient control in view of valve stiction: Extension of a Kalman-based FTC scheme[J]. Computer Aided Chemical Engineering,2010,28(2): 547-552. |
| [32] | Zhou K,Doyle J,Glover K. Robust and optimal control[M]. Upper Saddle River,NJ,USA: Prentice-Hall,1996. |
| [33] | Cao C,Hovakimyan N. Design and analysis of a novel adaptive control architecture with guaranteed transient performance[J]. IEEE Transactions on Automatic Control,2008,53(3): 586-591. |
| [34] | 王冬来,吕强,刘峰,等. 基于自适应方法的四旋翼飞行器纵向控制[J]. 弹箭与制导学报,2011,31(6): 37-40. Wang D L,Lü Q,Liu F,et al. Quadrotor longitudinal controller based on adaptive control method[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2011,31(6): 37-40. |
| [35] | Sipser M. Introduction to the theory of computation[M]. 3rd ed. Boston,MA,USA: Cengage Learning Publishing,2012. |
| [36] | Holling C S. Resilience and stability of ecological systems[J]. Annual Review of Ecological Systems,1973,4(7): 1-23. |
| [37] | Werner E,Smith R. Vulnerable but invincible: A longitudinal study of resilient children and youth[M]. New York,USA: McGraw-Hill,1982. |
| [38] | Holling C S. The resilience of terrestrial ecosystems: Local surprise and global change[M]. Cambridge,UK: Cambridge University Press,1986: 292-317. |
| [39] | Holling C S. What barriers? What bridges? In: Barriers and bridges to the renewal of ecosystems and institutions[M]. New York,USA: Columbia University Press,1995: 1-23. |
| [40] | Pimm S L. The complexity and stability of Ecosystems[J]. Nature,1984,307 (26): 321-326. |
| [41] | Carlson J M,Doyle J. Complexity and robustness[C] //Proceedings of the National Academy of Science-Self-Organized Complexity in the Physical,Biological,and Social Sciences. Piscataway,NJ,USA: IEEE,2002: 2538-2545. |
| [42] | Jen E. Stable or robust? What is the difference? Robust design: A repertoire of biological,ecological,and engineering case studies[M]. Oxford,UK: Oxford University Press,2005: 7-20. |
| [43] | Levin S A,Lubchenco J. Resilience,robustness,and marine ecosystem-based management[J]. BioScience,2008,58(1): 27-32. |
| [44] | Miller A,Xiao Y. Multi-level strategies to achieve resilience for an organization operating at capacity: A case study at a trauma centre[J]. Cognition,Technology and Work,2007,9(1): 51-66. |
| [45] | Boring R L. Reconciling resilience with reliability: The complementary nature of resilience engineering and human reliability analysis[C] //Proceedings of the 53rd Annual Meeting on Human Factors and Ergonomics Society. Berlin,Germany: Springer,2009: 1589-1593. |
| [46] | Serugendo G D,Fitzgerald J A,Romanovsky A,et al. A meta-based architectural model for dynamically resilient systems[C] //Proceedings of the 2007 ACM Symposium on Applied Computing. New York,NJ,USA: ACM,2007. |
| [47] | Villez K,Venkatasubramanian V,Garcia H,et al. Achieving resilience in critical infrastructures: A case study for a nuclear power plant cooling loop[C] //Proceedings of the 3rd International Symposium on Resilient Control Systems. Piscataway,NJ,USA: IEEE,2010: 49-52. |
| [48] | Mili L. Taxonomy of the characteristics of power system operating states[C] //2nd NSF-VT Resilient and Sustainable Critical Infrastructures Workshop. Berlin,Germany: Springer,2011: 1-6. |
| [49] | Manshaei M,Zhu Q,Alpcan T,et al. Game theory meets network security and privacy[J]. ACM Computing Surveys,2010,45(3): 1-42. |
| [50] | Cárdenas . From CRCs to resilient control systems: Differentiating between Reliability and security for the protection of cyber-physical systems[C] //Conference on High Confidence Networked Systems (HiCoNS) at CPSWeek 2014. New York,NJ,USA: ACM,2014: 125-126. |
| [51] | Anderson R S. Cyber security and resilient systems[C] //Proceedings of the 50th Annual Meeting of Institute of Nuclear Materials Management. Piscataway,NJ,USA: IEEE,2009: 1-10. |
| [52] | Arruda M. Dynamic inverse resilient control for damaged asymmetric aircraft: Modeling and simulation[D]. Wichta State,USA: Wichta State University,2007. |
| [53] | Lundberg J,Johansson B. Resilience,stability and requisite interpretation in accident investigations[C] //2nd Symposium on Resilience Engineering. Piscataway,NJ,USA: IEEE,2006: 191-198. |
| [54] | Costa W S,Voshell M ,Branlat M,et al. Resilience and brittleness in a nuclear emergency response simulation: Focusing on team coordination activity[C] //Proceedings of the 3rd Resilience Engineering Symposium. Piscataway,NJ,USA: IEEE,2008: 47-54. |
| [55] | Wolter K,Avritzer A. Resilience assessment and evaluation of computing systems[M]. Berlin,Germany: Springer-Verlag,2012: 6-23. |
| [56] | Dong W,Yan L,Jafari M,et al. An integrated security system of protecting smart grid against cyber attacks[C] //Proceedings of Innovative Smart Grid Technologies (ISGT). Piscataway,NJ,USA: IEEE,2010: 1-7. |
| [57] | Gu Q,MendonÇa D. Patterns of group information seeking in a simulated emergency response environment[C] //Proceedings of the 2nd International ISCRAM Conference. Piscataway,NJ,USA: IEEE,2005: 109-116. |
| [58] | Weimer J,Bezzo N,Pajic M,et al. Resilient parameter-invariant control with application to vehicle cruise control[M] //Lecture Notes in Control and Information Sciences. Berlin,Germany: Springer-Verlag,2013: 197-216. |
| [59] | Stevens L M. Next generation nuclear plant resilient control system functional analysis[R]. Idaho Falls,USA: Idaho National Laboratory,2010. |
| [60] | Bruno dos Santos F,Gomes J O,da Silva Borges M R,et al. Resilient control of a decision support system for emergency simulation at nuclear power plant[C] //Proceedings of the 2011 15th International Conference on Computer Supported Cooperative Work in Design. Piscataway,NJ,USA: IEEE,2011: 665-668. |



