1 引言
垂直起降(vertical take-off and landing,VTOL)飞机作为一种新型飞行器,可以实现自由起落,突破跑道的限制,具有重要的军用及民用前景和价值. 作为一种典型的多输入多输出、 强耦合、 非最小相位的非线性对象,VTOL飞机在控制领域一直是许多学者研究的热点和难点. 现有的研究成果主要集中在跟踪控制[1, 2, 3, 4]和稳定性控制[5, 6, 7]. 由于垂直飞行过程中的控制输入主要依靠推力发动机,其复杂的结构以及高度的耦合,发生故障的可能性较高,且故障会对飞行品质造成严重影响,因此针对VTOL飞机的容错控制研究,显得尤为必要,但是目前很少有文献考虑到相应的容错控制问题.
故障诊断在于及时检测并识别出故障,而容错控制是基于识别出的故障信息,通过容错控制器的调节,使得故障系统保持满意或者至少能接受的性能指标,经过几十年的发展,许多领域的故障诊断和容错控制的研究都取得了很大的发展[8, 9, 10, 11, 12, 13, 14, 15]. 在很多情形下,故障往往伴随着未知扰动同时出现,这就加大了诊断以及容错的难度[16, 17]. 文[16]中提出一种基于干扰和故障解耦的级联观测器来实现不同信息的分别估计. 文[17]提出了一种复合抗干扰鲁棒容错控制策略,使得微型航天器的控制系统能够有效地诊断系统时变故障的同时,也能够有效地抑制干扰,增强系统的鲁棒性.
非线性非最小相位系统由于特有的性质,一直是容错控制的难点,相应的成果也很少[18, 19]. 文[18]中针对单输入单输出非最小相位系统存在的各种不确定性和故障,提出了一种切换滑模容错控制方法,取得了不错的效果,但是切换滑模的设计较为复杂且不易推广到多输入多输出的系统中. 文[19]提出一种基于T-S模糊模型的鲁棒容错控制方法,实现了容错控制,但是也存在设计过程过于复杂、 控制器不易实现等不足,而且类似的成果还鲜见报道. 作者前期的相关工作主要是针对不同系统的不同故障,提出了相应的诊断及容错控制策略[20, 21],但也很少涉及到非最小相位的容错控制问题.
因此,本文在作者以及前人的相关研究基础上进行拓展,针对非线性非最小相位的VTOL飞机容错跟踪控制问题,综合考虑实际垂直飞行环境中存在的不确定扰动和推力输入通道执行器故障的情形,提出一种基于级联观测器和积分滑模[22]技术的鲁棒容错控制方案,有效检测故障和干扰两种信息,补偿它们对系统轨迹跟踪性能的影响,改善系统的稳定性.
2 问题提出 2.1 飞机模型本文研究对象为垂直起降飞机[1],飞机的纵向平面三自由度动力学方程如下:
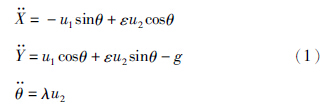
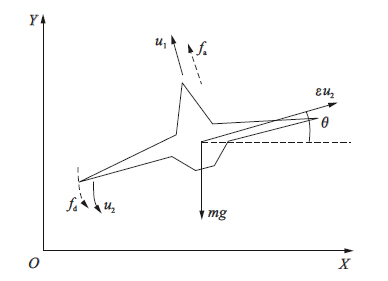 |
| 图 1 垂直起降飞机Fig. 1 VTOL aircraft |
在实际的垂直起降飞行过程中,VTOL飞机会受到外部的诸多不确定干扰的影响,比如风速和气流等与飞机滚转角相耦合的因素会直接影响到飞机的3个输出,本文把这一类干扰建模为fd(t).
飞机的升力主要是由机体底部的推力矢量发动机产生的推力u1通道提供,由于推力通道的结构复杂,相应的执行机构较多,出现故障的可能性相对较大,因此本文考虑推力通道的执行器加性故障,将其建模为fa(t). 则带有外部干扰的故障系统模型为
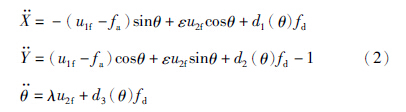
选取变量替换
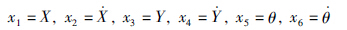

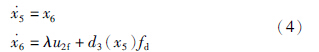
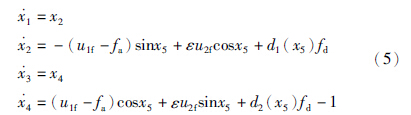
本文的控制目标是设计鲁棒容错控制器,使得系统输出x1(t)和x3(t)能够准确地跟踪给定的参考轨迹yd(t)=[Xd(t),Yd(t)]T,同时机体的滚转角θ=x5→0.
3 观测器设计本节设计一种新颖的级联观测器系统,如图 2所示,其中uf=(u1f,u2f)T为控制输入向量. 观测器系统由两个级联的观测器组成,前一个是干扰观测器,用来估计未知干扰; 后一个是故障诊断观测器,用来估计推力通道的故障信息.
 |
| 图 2 级联观测器结构图Fig. 2 Structure of cascade observors |
假设1 外部干扰是未知的,但是满足有界条件

假设2 飞机的飞行速率不可测,但3个输出量可测.
注1 本文研究对象为VTOL飞机的垂直起降飞行过程,不考虑超机动飞行,此时外部干扰的幅值通常都是有界的,因此假设1的条件通常都能满足. 系统的3个输出量可以通过相应的传感器和定位系统获得.
3.1 干扰观测器针对无故障的子系统(4),设计滑模干扰观测器如下:
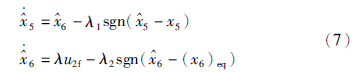
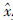 5和
5和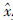 6是状态量x5和x6的观测值,sgn(·)是符号函数,λ1和λ2是切换项增益,其中增益λ2满足
6是状态量x5和x6的观测值,sgn(·)是符号函数,λ1和λ2是切换项增益,其中增益λ2满足
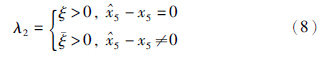
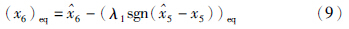
定理1 针对系统(4)和观测器(7),选择合适的增益,能够使得状态和干扰的估计值渐近收敛于其实际值.
证明 记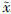 5=
5=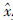 5-x5和
5-x5和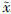 6=
6=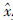 6-x6为状态观测误差,则观测误差动态系统为
6-x6为状态观测误差,则观测误差动态系统为

第一步: 在0≤t≤t1时间段,假设在初始时刻满足x5≠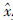 5,因此λ2=
5,因此λ2=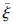 ,误差系统可重写为
,误差系统可重写为
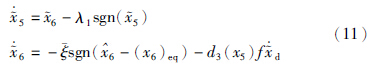
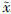 25/2,对时间求导得
25/2,对时间求导得
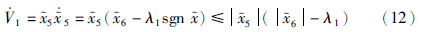
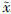 6|max时,则在时间t1内,观测误差5能够收敛于滑动平面
6|max时,则在时间t1内,观测误差5能够收敛于滑动平面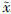 5=0.
5=0.
第二步: 在t1<t≤t2时间段时,有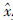 5→x5和λ2=ξ,
5→x5和λ2=ξ,

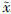 5)eq=
5)eq=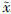 6为等效控制项.
6为等效控制项.
再取李亚普诺夫函数V2=(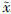 25+
25+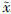 26)/2,对时间求导得
26)/2,对时间求导得
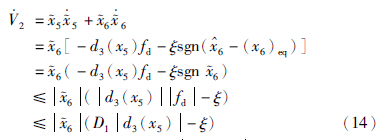
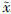 6能够在时间t2内收敛至滑模平面
6能够在时间t2内收敛至滑模平面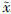 6=0.
6=0.
综上分析,选择合适的切换项增益,在经过时间t=t2之后,观测误差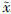 5和
5和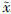 6都将收敛至零,实现了状态的精确估计. 且对于所有的t2≤t,都有
6都将收敛至零,实现了状态的精确估计. 且对于所有的t2≤t,都有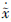 6=0. 假定函数d-13(x5)非奇异,由(13)式得干扰的估计值为
6=0. 假定函数d-13(x5)非奇异,由(13)式得干扰的估计值为
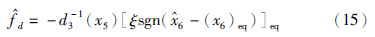
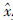 6-(x6)eq)]eq,可得到
6-(x6)eq)]eq,可得到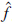 d→fd,可精确地估计出干扰值. 证毕.
3.2 故障诊断观测器
d→fd,可精确地估计出干扰值. 证毕.
3.2 故障诊断观测器
针对受故障影响的子系统(5),基于3.1节干扰信息的估计,提出故障诊断观测器,用于重构故障信息. 首先,定义新的故障变量和干扰变量为
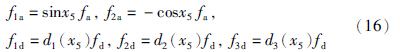
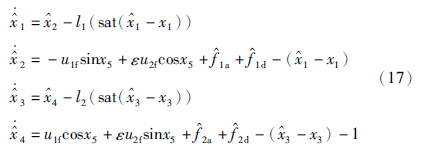
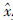 i(1≤i≤4)为状态变量xi的观测值,l1和l2为增益,sat(·)是饱和函数.
i(1≤i≤4)为状态变量xi的观测值,l1和l2为增益,sat(·)是饱和函数. 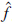 ja(j=1,2)为故障变量fja的估计值,
ja(j=1,2)为故障变量fja的估计值,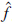 kd(k=1,2,3)为干扰变量fkd的估计值.
kd(k=1,2,3)为干扰变量fkd的估计值.
记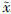 i=
i=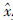 i-xi为状态估计误差,
i-xi为状态估计误差,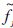 ja=
ja=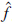 ja-fja为故障估计误差. 故障估计算法选择为
ja-fja为故障估计误差. 故障估计算法选择为

定理2 对于子系统(5)和观测器(17),选择算法(18),则状态和故障的估计值能渐近收敛于其实际值.
证明 观测误差的动态方程为
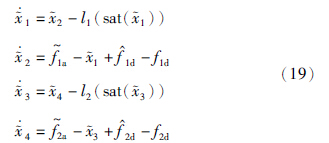
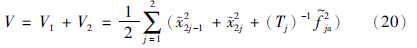
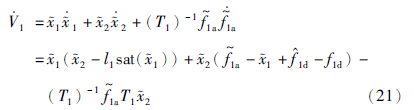
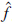 d→fd,进一步可得
d→fd,进一步可得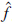 1d→f1d. 式(21)可变为
1d→f1d. 式(21)可变为
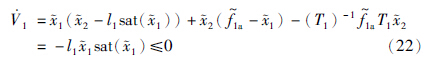
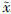 1≠0,都有
1≠0,都有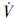 1<0,即当t→∞时,有
1<0,即当t→∞时,有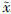 1→ 0. 类似地,也有
1→ 0. 类似地,也有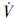 2≤0. 那么,
2≤0. 那么,
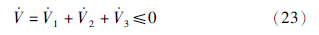
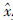 i→xi,
i→xi,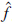 ja→fja. 通过变换(16),可得
ja→fja. 通过变换(16),可得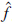 a→fa. 结论得证.
4 容错控制器设计
4.1 坐标变换与零动态
a→fa. 结论得证.
4 容错控制器设计
4.1 坐标变换与零动态
初始故障系统(3)非奇异解耦矩阵[3]为

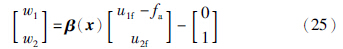
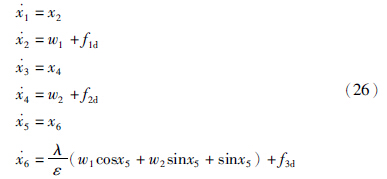

本节对系统(26)进行解耦. 首先,选择误差变量
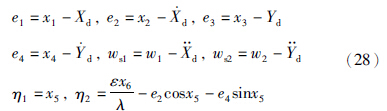
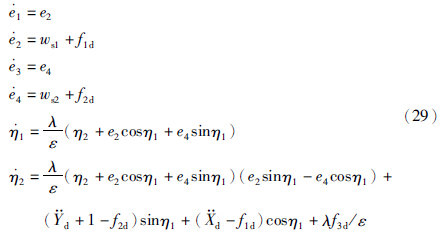

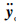 d=(
d=(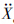 d,
d,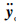 d)T为期望轨迹的二阶导数,Γ(η,e,
d)T为期望轨迹的二阶导数,Γ(η,e,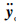 d)为非线性项.
d)为非线性项. 由于
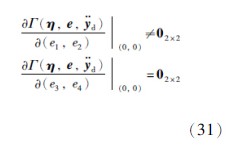
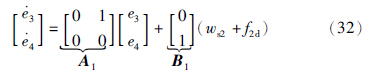
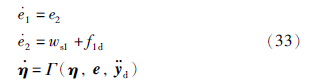
针对受扰动和故障影响的跟踪误差系统,设计两个局部控制律来分别镇定两个跟踪子系统,再利用可逆的控制变换,设计全局容错控制律来使得整个故障系统渐近跟踪给定参考轨迹.
4.3.1 最小相位子系统控制基于前述设计的级联观测器系统和系统解耦,可以借助线性最优控制[22]方法来实现最小相位跟踪子系统的镇定,设计最优控制律
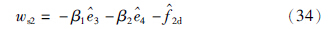
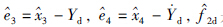 是干扰变量f2d的估计值,可由干扰观测器获得. (β1,β2)=K1为最优反馈增益,P1是满足Riccati方程
是干扰变量f2d的估计值,可由干扰观测器获得. (β1,β2)=K1为最优反馈增益,P1是满足Riccati方程
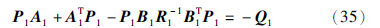
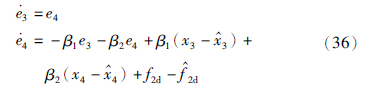
 3→x3,
3→x3, 4→x4和
4→x4和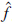 2d→f2d,则闭环跟踪系统(36)在原点渐近稳定. 即对于任意二阶可导的期望输出信号Yd(t),当t→∞时,有Y(t)→Yd(t)和
2d→f2d,则闭环跟踪系统(36)在原点渐近稳定. 即对于任意二阶可导的期望输出信号Yd(t),当t→∞时,有Y(t)→Yd(t)和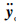 (t)→
(t)→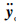 d(t),实现了飞机垂直坐标的有效跟踪.
4.3.2 非最小相位子系统控制
d(t),实现了飞机垂直坐标的有效跟踪.
4.3.2 非最小相位子系统控制
对于非最小相位子系统,采用线性化的方法进行变换. 记变量z=(e1,e2,ηT)T,式(33)可以改写为
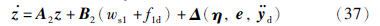
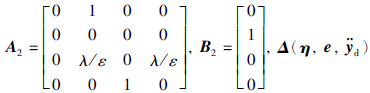 为线性化之后剩余的高阶项,其形式为
为线性化之后剩余的高阶项,其形式为
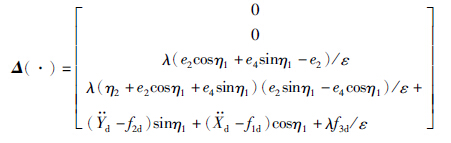
针对非最小相位部分(37),设计如下控制律
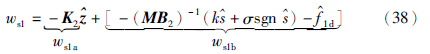
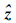 是状态量z的估计值,M∈R1×4为增益,且满足MB2非奇异. K2=R-12BT2P2是最优反馈增益. R2、 Q2和P2的定义同式(35).
是状态量z的估计值,M∈R1×4为增益,且满足MB2非奇异. K2=R-12BT2P2是最优反馈增益. R2、 Q2和P2的定义同式(35). 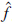 1d是f1d的估计值,k是正的常数增益,σ是滑动切换项的增益.
1d是f1d的估计值,k是正的常数增益,σ是滑动切换项的增益. 积分滑模面[23]定义为
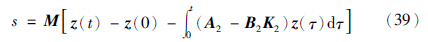
定理3 针对系统(37),选择控制律(38),若滑动切换项的增益σ满足条件
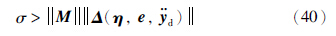
证明 选取李亚普诺夫函数为


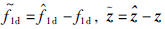 ,由观测器(7)和(17)可知,
,由观测器(7)和(17)可知,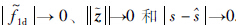 . 消去趋于零的项,再把式(40)的条件代入式(42),则有
. 消去趋于零的项,再把式(40)的条件代入式(42),则有
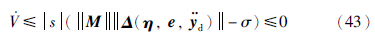
定理3表明,对于任意二阶可微的期望Xd(t),当t→∞时,都有X(t)→Xd(t)和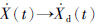 ,同时也有η1(t)→ 0和η2(t)→ 0,即滚转动态渐近稳定.
,同时也有η1(t)→ 0和η2(t)→ 0,即滚转动态渐近稳定.
由故障诊断观测器可以得到故障变量的估计值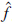 1a和
1a和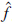 2a,为方便设计系统(3)的容错跟踪控制律,需要得到初始故障
2a,为方便设计系统(3)的容错跟踪控制律,需要得到初始故障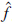 a的估计信息,由式(16)的变换可得
a的估计信息,由式(16)的变换可得

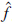 a的连续性.
a的连续性. 定理4 针对初始故障系统(3),设计鲁棒容错控制律

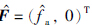 为重构之后的故障向量. 则系统(3)的输出能够渐近跟踪给定的期望轨迹.
为重构之后的故障向量. 则系统(3)的输出能够渐近跟踪给定的期望轨迹. 证明 证明过程和上文定理3的证明类似,故略去.
5 仿真结果在Matlab/Simulink环境下建立VTOL飞机控制系统的仿真模型,进行仿真实验分析,以验证本文所设计的控制器的有效性. 仿真时间为150 s,给定的位置参考轨迹为Xd(t)=0.3+0.05sin(0.2t)(km),Yd(t)=0.1cos(0.1t)(km). 系统参数选择为ε=0.5,λ=1; 外部扰动和相应的耦合函数选取为
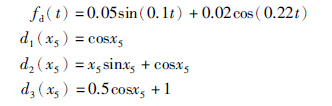
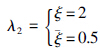 ; 故障观测器增益为l1=3,l2=5,T1=T2=5; 初始状态为x(0)=(0.1,0,0,0,0,0)T; 选取矩阵Q1=diag(100,100),Q2=diag(10,10,10,10),R1=50,R2=120,可计算得最优控制部分的增益为K1=(1.414 2,2.197 4),K2=(-0.288 7,3.677 2,3.504,4.947). 积分滑模控制部分的增益为M=(1,2.5,1,1),k=σ=5. 故障变换参数为W=0.01,μ=0.05. 推力通道的加性故障选取为
; 故障观测器增益为l1=3,l2=5,T1=T2=5; 初始状态为x(0)=(0.1,0,0,0,0,0)T; 选取矩阵Q1=diag(100,100),Q2=diag(10,10,10,10),R1=50,R2=120,可计算得最优控制部分的增益为K1=(1.414 2,2.197 4),K2=(-0.288 7,3.677 2,3.504,4.947). 积分滑模控制部分的增益为M=(1,2.5,1,1),k=σ=5. 故障变换参数为W=0.01,μ=0.05. 推力通道的加性故障选取为
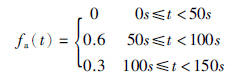
为了进一步验证本文所提算法的优越性,本文把所设计的最优控制加积分滑模控制(OISMC)的方法与文[2]中提出的传统反馈加滑模控制(SMC)的方法在故障的条件下进行容错跟踪控制效果对比. 具体仿真结果如图 3~图 5所示.
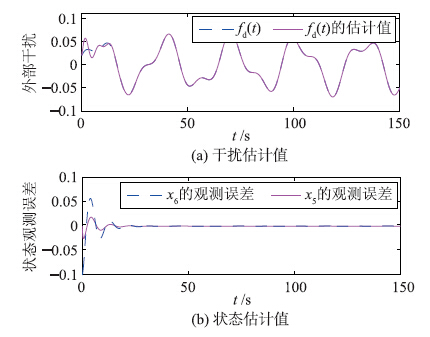 |
| 图 3 干扰观测器的仿真曲线Fig. 3 The simulation curves of disturbance observor |
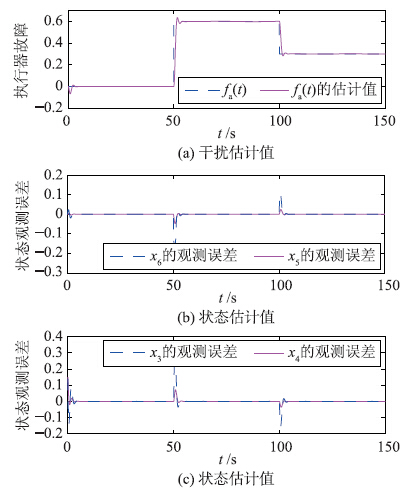 |
| 图 4 故障诊断观测器的仿真曲线Fig. 4 The simulation curves of fault diagnosis observor |
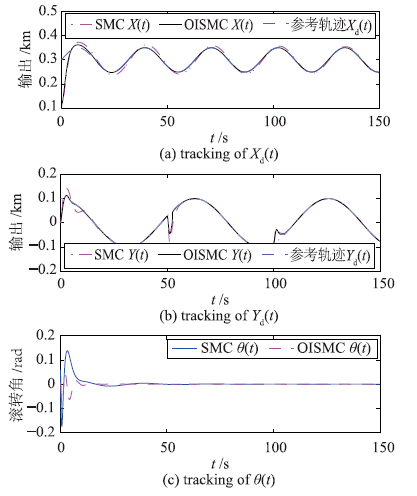 |
| 图 5 容错输出跟踪Fig. 5 Fault tolerant output tracking |
图 3和图 4首先给出了级联观测器的仿真结果.
从图 3中可以看出,所设计的滑模干扰观测器能够精确快速地逼近未知干扰和状态.
利用干扰的估计值来进行故障重构,当故障发生后,利用设计的故障观测器迅速检测出故障的相关信息,再经过式(44)的变换,得到初始故障信号fa(t)的重构信息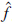 a(t),仿真曲线如图 4所示.
a(t),仿真曲线如图 4所示.
图 4是执行器加性故障及相应的状态的仿真曲线. 从图中可以看出,故障的估计值能够快速地收敛到其真实值,而且超调较小; 在故障发生的时刻,状态的观测值会受到影响而偏离其真实值,但会很快收敛到其真实值.
为了验证本文所提控制器的优越性,下面针对系统的容错输出跟踪性能进行两种方法的对比,本文采用的控制器为OISMC,文[2]中的控制器为SMC,相应的对比仿真结果如图 5所示.
从图 5可以看出,故障系统在OISMC和SMC作用下均能够稳定地跟踪给定的轨迹且稳定滚转角. 但是本文所提出的OISMC方法和传统的SMC方法相比,能够使得故障系统的外部输出更加快速和精确地跟踪参考轨迹,同时也能更好地镇定滚转角. 通过对比,表明了本文的容错控制器控制性能的优越性,满足系统容错跟踪的性能要求.
6 结论本文研究了存在外部干扰的VTOL飞机一类推力输入通道执行器故障的鲁棒容错控制问题. 设计了基于级联观测器的最优积分滑模容错控制器,补偿干扰和故障对系统跟踪性能的影响,系统在控制器作用下能够有效地跟踪给定参考轨迹且飞机的滚转角稳定,具有较强的鲁棒性. 最后通过与传统的滑模控制方法的对比,进一步显示了本文所提方法的优越性.
| [1] | Al-Hiddabi S A,McClamroch N H. Output tracking for nonlinear non-minimum phase VTOL aircraft[C] //Proceedings of the 37th IEEE Conference on Decision and Control. Piscataway,NJ,USA: IEEE,1998: 4573-4578. |
| [2] | Wang X H,Liu J K,Cai K Y. Tracking control for a velocity sensor-less VTOL aircraft with delayed outputs[J]. Automatica,2009,45(12): 2876-2882. |
| [3] | Wang X H. Takeoff/landing control based on acceleration measurements for VTOL aircraft[J]. Journal of the Franklin Institute,2013,350(10): 3045-3063. |
| [4] | Su S,Lin Y. Robust output tracking control for a velocity sensor-less vertical take-off and landing aircraft with input disturbances and unmatched uncertainties[J]. International Journal of Robust and Nonlinear Control,2012. |
| [5] | Olfati-Saber R. Global configuration stabilization for the VTOL aircraft with strong input coupling[J]. IEEE Transactions on Automatic Control,2002,47(11): 1949-1952. |
| [6] | Chemori A,Marchand N. A prediction-based nonlinear controller for stabilization of a non-minimum phase PVTOL aircraft[J]. International Journal of Robust and Nonlinear Control,2008,18(8): 876-889. |
| [7] | Isidori A. Nonlinear control systemsⅡ[M]. Berlin,Germany: Springer,1999. |
| [8] | Xu Y,Jiang B,Tao G,et al. Fault tolerant control for a class of nonlinear systems with application to near space vehicle[J]. Circuits,Systems,and Signal Processing,2011,30(3): 655-672. |
| [9] | 姚利娜,薛霄,姜斌. 序列连续系统的容错控制[J]. 信息与控制,2013,42(1): 13-17. Yao L N,Xue X,Jiang B. Fault tolerant control for a sequential continuous system[J]. Information and Control,2013,42(1): 13-17. |
| [10] | 段海滨,于秀芬,王道波. 一种现代航天器飞行控制系统及其容错技术研究[J]. 电光与控制,2004,11(3): 40-43. Duan H B,Yu X F,Wang D B. Research on spacecraft flight control system and its fault-tolerant technique[J]. Electronics Optics and Control,2004,11(3): 40-43. |
| [11] | 白铭珍,吴淮宁. 非线性主动容错控制系统H∞模糊控制器设计[J]. 航空学报,2008,29(5): 1281-1287. Bai M Z,Wu H N. H∞ fuzzy controller design for nonlinear active fault tolerant control systems[J]. Acta Aeronautica et Aeronautica Sinica,2008,29(5): 1281-1287. |
| [12] | Zhang X,Polycarpou M M,Parisini T. Fault diagnosis of a class of nonlinear uncertain systems with Lipschitz nonlinearities using adaptive estimation[J]. Automatica,2010,46(2): 290-299. |
| [13] | 谢德晓,张登峰,黄鹤,等. 一类不确定网络控制系统的鲁棒容错控制[J]. 信息与控制,2010,39(4): 472-478. Xie D X,Zhang D F,Huang H,et al. Robust fault-tolerant control for a class of uncertain networked control systems[J]. Information and Control,2010,39(4): 472-478. |
| [14] | Wang T,Xie W,Zhang Y. Sliding mode fault tolerant control dealing with modeling uncertainties and actuator faults[J]. ISA Transactions,2012,51(3): 386-392. |
| [15] | 王青,王明明,董朝阳. 一类降阶故障检测滤波器设计及其在飞行器中的应用[J]. 宇航学报,2013,34(1): 61-68. Wang Q,Wang M M,Dong C Y. Design of a kind of reduced-order fault detection filtering algorithm and its application in space vehicles[J]. Journal of Astronautics,2013,34(1): 61-68. |
| [16] | Aldeen M. Fault,state,and unknown input reconstruction in nonlinear systems using sliding mode observers[J]. Journal of Dynamic Systems,Measurement,and Control,2011,133(1): 1-9. |
| [17] | 乔建忠,郭雷,雷燕婕,等. 微纳卫星姿态控制系统的精细抗干扰容错控制方法[J]. 中国科学: 信息科学,2012,42(11): 1327-1337. Qiao J Z,Guo L,Lei Y J,et al. Subtle anti-disturbance tolerant control of attitude control systems for microsatellites[J]. Scientia Sinica: Information Sciences,2012,42(11): 1327-1337. |
| [18] | Wang Y,Zhou D,Gao F. Robust fault-tolerant control of a class of non-minimum phase nonlinear processes[J]. Journal of Process Control,2007,17(6): 523-537. |
| [19] | Chadli M,Aouaouda S,Karimi H R,et al. Robust fault tolerant tracking controller design for a VTOL aircraft[J]. Journal of the Franklin Institute,2012,350(9): 2627-2645. |
| [20] | 姜斌,冒泽慧,杨浩,等. 控制系统的故障诊断与故障调节[M]. 北京: 国防工业出版社,2009: 1-55. Jiang B,Mao Z H,Yang H,et al. Falut diagnosis and fault accommodation for control systems[M]. Beijing: National Defense Industry Press,2009: 1-55. |
| [21] | 姜斌,杨浩. 飞控系统主动容错控制技术综述[J]. 系统工程与电子技术,2009,29(12): 2106-2110. Jiang B,Yang H. Survey of the active fault-tolerant control for flight control system[J]. Systems Engineering and Electronics,2009,29(12): 2106-2110. |
| [22] | 高超,高存臣. 复合非线性反馈积分滑模控制器的设计[J]. 信息与控制,2014,43(1): 19-23. Gao C,Gao C C. Integral sliding mode controller design based on composite nonlinear feedback[J]. Information and Control,2014,43(1): 19-23. |
| [23] | Pang H,Yang X. Robust optimal sliding mode tracking control for a class of uncertain nonlinear MIMO systems[J]. Journal of Applied Mathematics,2013(2013): ID 863168. |



