1 引言
图像修复(inpainting)[1]技术是当前图像处理技术的一个研究热点. 它在珍贵艺术品保护,去除图像多余信息及数字图像传输失真修复等方面有着重大应用价值.
现有数字图像修复主要有采用几何和纹理合成等特征的图像修复方法[1]. 基于几何特征的图像修复采用的主要思想是先选定图像待修复区域,再利用待修复区域周围已知信息,通过传递、 扩散以及结合等方式,将待修复区域边缘信息按一定规律延伸至受损区域. 采用该思想的方法主要包括: 基于三阶偏微分方程(PDE)的方法、 曲率驱动扩散模型[2]、 全变分模型[3]、 欧拉弹性模型[4]、 Mumford-Shah模型及其扩展的Mumford-Shah-Euler模型等[5]. 由于这些方法在数值实现时都需引入大量迭代运算,以致其运算复杂度较高及运算时间较长,在实用中受限,无法大规模推广. 因此,如何高效快速修复受损图像,已成为当前迫切需要解决的关键问题[6, 7]. 针对该问题,本文提出了基于像素权值的高效小波图像修复算法. 它是一种快速非迭代修复方法: 算法从受损区域边界开始,将待修复区信息逐步向内推进,同时修复各边界离散像素点,直至整个待修复区域全部修复.
小波理论是20世纪80年代开始发展的信号处理方法[8]. 由于其特有的多分辨率与时频局部分析特性,在通信信号处理、 图像分析等领域获得广泛应用. 本文将多分辨率思想应用于图像修复: 先对图像进行小波分解得到图像不同频率成分,再处理分解后的各小波分量,并由小波系数重构而获得修复后的图像. 仿真表明: 该算法在修复后图像视觉效果类似的情况下,运行所需时间比传统算法大为缩短,且复杂度也有较大降低,便于高效修复图像.
2 基于像素权值的修复算法在数字图像应用实践中,常有去除多余物体、 划痕等修复需求. 根据文[10, 11]可知,在对图像进行修复之前,要对待修复图像预处理,即对目标区域进行人工判断,从而使得待修复区域的错误数据不计入算法的运算中去. 对图像预处理后可设I为待修复图像,Ω为受损区域,即待修复目标;∂Ω为修复区边界; 边界上待修复点p的邻域记为Ψ(p),即以待修复点p为中心的图像区域. 为便于提取图像待修复区域,一般将输入灰度图像的待修复区域像素值置为0或255,然后根据图像像素值自动标记待修复区域. 算法中用一个掩模图像(Mask)来标记待修复区域,其掩模图像为二值图像,待修复区域标记为1,已知区域标记为0. 算法对于待修复区域内的像素值进行修复,根据掩模图像中的位置提取待修复区域的边界,然后根据待修复区域边界的已知像素信息由边界向内推进,如图 1所示.
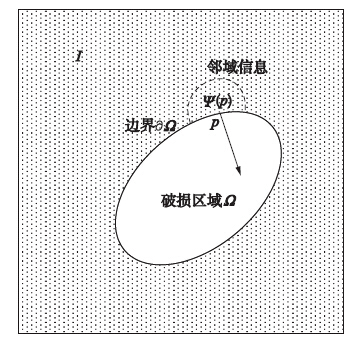 |
| 图 1 典型受损图像示意图Fig. 1 Typical damaged image |
本算法为非迭代快速修复算法. 为了降低修复中的误差,并提高修复效率,修复过程采用从待修复区域边界Ω开始,由外向内,逐层推进进行. 每层修复完并更新该层像素值后,重新提取边界,继续向内推进,直至整个受损区域被修复完毕[12, 13, 14]. 针对传统的基于偏微分方程(partial differantial equation,PDE)的BSCB(Bertalmio Sapiro Caselles Bellester)模型、 整体变分(total variation,TV)方法、 基于曲率的扩散(curvature driven diffusions,CDD)模型等图像修复算法,它们在数值实现过程中都需引入大量迭代运算,以致其运算复杂度较高,算法时间成本过高; 而本文算法在信息推进的过程中无需重复迭代,一层修复完毕后立即向下一层推进,不必再进行重复计算,因此算法耗时上相比传统算法大大降低.
在对单个受损像素点进行修复时,首先如图 2所示选取邻域像素模板[12],再对邻域像素模板内已知像素值计算其像素权值. 最后,根据计算所得像素权值及模板内已知像素值计算所得受损点像素值. 具体如图 2所示. 实际修复选取以待修复点p为中心的5×5大小邻域像素模板,q点为邻域像素模板内已知点,pq为待修复点到已知点连线方向向量,N⊥p为已知点q点的梯度方向.
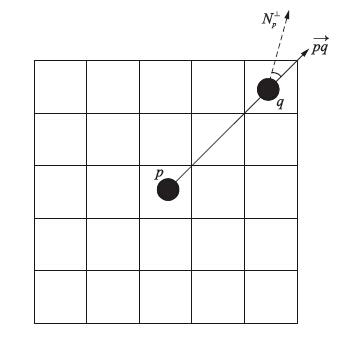 |
| 图 2 待修复点邻域像素模板示意图Fig. 2 Adjacent pixel template of a point to be inpainted |
如图 2所示,I(p)为p点的像素值. 在此,定义像素权函数如式(1)所示:
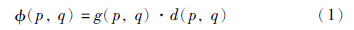
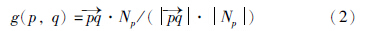
由式(2)可得: 当q点在等照度线方向Np上时,g(p,q)=1,即方向向量与等照度线重合. 此时,g(p,q)最大,该已知点对待修复点的影响也最大; 而当q点离等照度线越远时,g(p,q)越小,则该点对待修复点的影响也越小. 式(3)中d(p,q)为像素距离影响因子. 其表现为已知点与待修复点距离远近对待修复点所造成的影响. 如已知像素点与待修复点越近,则其对待修复点影响越大,反之则影响越小. 因此,可定义像素距离影响因子为
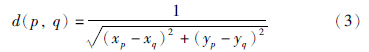
如把式(2)和式(3)代入式(1),则得像素权函数计算所得的像素权值. 再对邻域像素模板Ψ(p)内已知像素点进行权重赋值,φ(p,q)值越大,则说明该已知像素点对待修复点的影响越大,反之则影响越小. 最后,加权平均即可求得p点的像素值. 具体如式(4)所示:

受损像素点修复完毕后,更新该点像素值,继续下一个受损点修复. 一层修复完成后重新提取边界,进行下一层修复. 重复上述步骤,直到受损区域全部修复完毕.
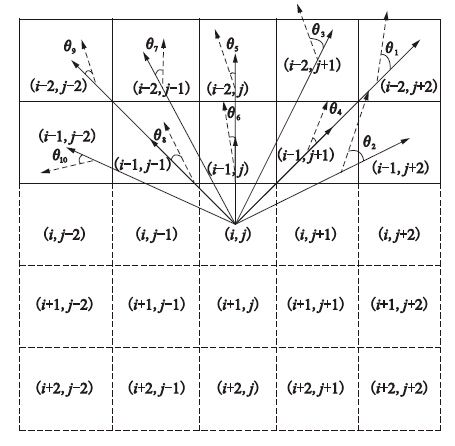
如图 3所示,点(i,j)为图像破损边缘处的待修复点,图中实线部分为已知像素点,虚线部分为破损像素点,即未知像素点,通过已知像素点的信息来修复破损像素点. 如图所示,θ1,…,θ10分别为已知像素点等照度线方向与该点方向向量的夹角,根据式(2)可知,θ越小,等照度线方向与该点方向向量越接近,则像素方向因子越大; 由式(3)可得,离待修复点(i,j)越近,像素距离影响因子越大. 把计算得到的像素方向影响因子和像素距离影响因子代入(1)式中可得,像素点(i-1,j)最后得到的像素权函数值最大. 然后把计算得到的像素权函数代入(4)式对应相乘,即以该已知点的像素值乘以其对应的像素权函数,其在图像中相应的意义为权函数越大的已知像素点对待修复点(i,j)的贡献越大,因此在图 3中的已知像素点中,像素点(i-1,j)对待修复点(i,j)的贡献最大,因此被赋予了更高的权重. 接着把已知像素点与其像素权函数对应相乘后的结果进行累加,权重越大的像素点在像素的累加中所占的影响越大,最后对其累加的结果进行权值均衡,保证修复得到的像素点最接近于图像的真实像素值. 通过像素方向影响因子和像素距离影响因子的双重约束,能够尽可能地精确重建出图像的像素值,使修复后图像更符合人类主观视觉评价.
 |
| 图 3 待修复点邻域像素模板分析示意图Fig. 3 Analysis of the adjacent pixel template of a point to be inpainted |
目前,小波变换(wavelet transform,WT)在信号处理与图像分析等领域获得广泛应用[7, 8, 9]. 对于任意二维图像f(x,y)∈L2(R×R),有:
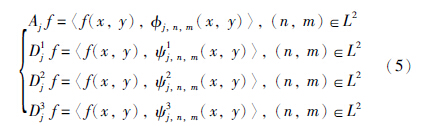
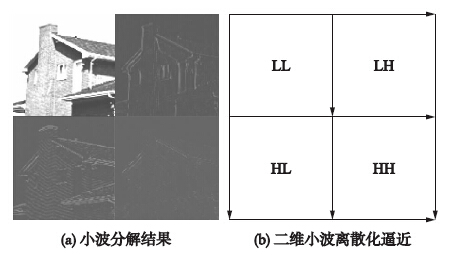 |
| 图 4 图像的一级小波分解Fig. 4 First scale wavelet decomposition for the image |
从图 4中还可得: 低频分量与其余3个分量对应位置信息相似,小波变换后各分量存在较强相关性. 由于图像信息主要集中在低频分量,故修复过程主要在低频分量进行. 在对图像进行小波分解后,图像低频分量为原始图像大小的1/4. 因此,修复区被缩小了,只需更短时间即可完成修复. 在完成低频分量修复后,将低频图像中已修复受损像素及周围领域像素取出,再对其水平、 垂直及对角方向进行滤波,然后填补到对应其余分量的图像. 最后,对图像小波重构,完成整个修复. 根据应用角度,一级小波分解足够满足多数图像修复要求[12].
3.2 基于像素权值的小波域修复算法从图 4中可得: 高频分量(LH,HL,HH)与低频分量(LL)对应位置信息相似. 因此,可把低频分量修复后信息滤波后,填补到其余对应位置的3个分量图.
根据上述分析,提出了基于像素权值高效小波修复算法. 首先,对图像进行小波分解. 由于图像信息主要集中在低频分量,而一级小波分解所得低频分量仅为原始图像大小的1/4,即相当于受损区域缩小为原先的1/4; 然后,利用基于像素权值方法对小波分解后的低频分量进行修复: 由于低频分量受损面积大为缩小,故修复所耗时间也大为缩短; 接着,根据低频与高频分量对应位置信息的相似性,对修复完成的低频分量滤波,把所得信息填补到其余3个对应分量图像; 最后,通过小波重构,得到最终修复的图像.
具体算法步骤如下:
(1) 读入图像和受损区域掩模,并对图像进行二维小波分解.
(2) 选取分解后图像低频部分,对低频部分待修复像素点计算其邻域像素权值,再根据计算所得像素权值和已知像素值,计算待修复点像素值,完成受损像素点修复.
(3) 对修复后低频部分进行水平、 垂直及对角方向滤波,再填补到对应其余3个分量.
(4) 将修复后的各个小波分量重构,最终获得修复完成图像.
4 仿真实验及分析为检验所提算法的有效性,从修复所消耗的时间及修复后图像的总体视觉效果两方面,对算法综合评价[12, 13, 14]. 微机仿真平台主要采用了Intel i5-2400四核1.58 G主频CPU及NVIDIA Geforce GT420显卡等组件,并利用Matlab软件(版本: 2011b)进行了仿真. 此外,在仿真中,主要选择了对照的BSCB、 TV及CDD算法,并与本算法进行了综合比较.
4.1 图像修复之划痕和文字去除图 5展示了一组图片划痕去除效果. 其中,5(a) 为待修复图像,5(b) 为BSCB算法修复结果,5(c) 为TV算法修复结果,5(d) 为CDD算法修复结果,5(e) 为本文算法修复结果. 因算法采用非迭代方式由受损区域边缘向内信息推进方式,故修复所耗时间相比其它传统算法大为缩短.
 |
| 图 5 划痕去除仿真图Fig. 5 Simulation image after nick eliminating |
从图 5划痕去除和图 6文字去除实验可得: 传统修复算法在对划痕及文字去除上有较满意的主观视觉效果. 但从表 1对比修复时间可见,传统算法所耗时间过长,特别是CDD算法,虽然修复后主观视觉效果最优,但修复时间太长,算法代价太高,不利于实际应用; 本算法在主观视觉效果上与传统算法修复效果类似,但修复时间却只有传统算法几分之一甚至几百分之一,故修复效率得到极大提升.
 |
| 图 6 文字去除仿真图Fig. 6 Simulation image after character eliminating |
| 实验图像 | 图片尺寸 | 缺损像素 | 修复时间/s | 峰值信噪比(PSNR) | ||||||
| BSCB | TV | CDD | Proposed | BSCB | TV | CDD | Proposed | |||
| Animal(图 5) | 512×512 | 4 651 | 31.147 0 | 83.487 | 611.049 7 | 5.481 | 42.299 8 | 45.017 6 | 45.606 5 | 40.096 9 |
| House(图 6) | 512×512 | 5 474 | 31.775 0 | 85.685 | 688.393 | 5.710 | 53.685 7 | 55.601 8 | 55.238 7 | 48.180 8 |
| Rock(图 7) | 512×512 | 10 096 | 31.980 0 | 129.268 | 1 184.076 | 5.851 | 21.468 7 | 38.929 8 | 38.952 6 | 36.293 0 |
| Lena(图 8) | 512×512 | 4 354 | 32.047 3 | 81.232 | 634.864 | 3.331 | 27.303 9 | 49.029 8 | 49.243 6 | 47.128 5 |
图 7和图 8分别为条形斑点去除和圆形斑点去除的示意图. 用传统算法和本算法分别对两种类型受损图像修复.
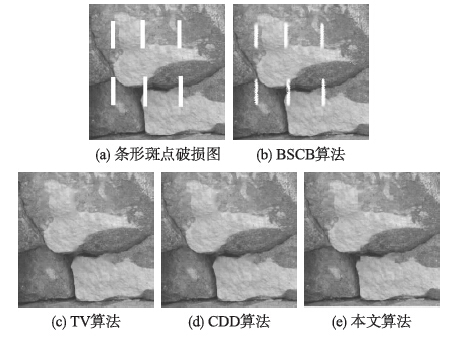 |
| 图 7 条形斑点去除仿真图Fig. 7 Simulation image after strip spot eliminating |
 |
| 图 8 圆形斑点去除仿真图Fig. 8 Simulation image after round spot eliminating |
由图 7和图 8得: 对于条形斑点破坏和圆形斑点破坏修复,由于受损区域面积较大,采用BSCB算法修复后会呈现明显亮斑,主观视觉效果较差; 而其它传统算法和本算法修复后主观视觉效果都较好,没有特别明显亮斑. 另从表 1记录的数据分析可知,对于BSCB算法,由于其对图像进行迭代,故修复时间与受损区域无直接关系,只和图像大小有关; TV算法和CDD算法所耗时间与图像大小及受损区域大小有直接关系; 而本文算法,由于只针对受损区域修复,故图像受损区域越小,修复所需时间也越短.
对表 1中的峰值信噪比进行纵向对比,峰值信噪比越高,修复后的图像质量越好[15, 16]. 从表 1中可以看到BSCB算法对于划痕和文字的修复效果较好,图像修复后的峰值信噪比较高,但是对于斑点破损的修复效果则较差,这与主观评价是相一致的; TV算法相对于BSCB算法来说修复效果上有一定程度的提升,但是缺陷也显而易见,算法耗时过长; 与TV算法类似,CDD算法修复后的图像峰值信噪比较为理想,但是同样是算法耗时过长,甚至达到本文算法耗时的百倍数量级; 本文算法在图像质量与传统算法类似的情况下,修复时间为传统算法的几十分之一甚至几百分之一,大大地提升了图像的修复效率; 图像质量方面由于小波重构中引入了部分噪声,因此部分PSNR(peak signal to noise ratio)指标上略有欠缺,但是图像主观视觉方面与传统算法相比几乎无区别,甚至优于部分算法. 与传统算法类似,在对图像进行修复前需要人工对待修复区域进行判定. 因此,对于大量需要待修复的图像,标定其待修复区域,操作上确实存在不便. 但是,对于用户体验方面,由于大部分用户无需同时修复大量图像,修复效率成为用户较关注的问题. 另外,对于部分图像需去除特定目标物的修复类型,计算机无法进行自动判断,仍需要人工进行预处理判定待修复区域,而本文算法以其修复后较好的图像质量及较高的修复效率有利于实际应用. 因此,综合修复后图像主观视觉效果、 修复时间及峰值信噪比因素,本文所提算法效率较高.
5 结论本文把图像修复问题映射到小波域,提出了基于像素权值的高效小波图像修复算法. 该算法与传统算法相比无需大量迭代,缩短了算法所耗时间. 算法先对图像进行小波分解,再找到图像待修复区域. 同时,根据待修复区域及其邻域像素值,计算相应的像素权值. 接着,用计算所得像素权值及邻域内已知像素值,完成对受损像素点的修复. 最后,对修复后图像进行小波重构. 在修复中,引入像素方向和像素距离影响因子来计算像素权值,从而达到提升图像视觉效果的目的. 仿真表明: 在图像修复效果相近时,本算法显著改善了修复效率并降低了复杂度. 综上所述,新算法相对传统算法,在计算代价上有较明显降低.
| [1] | Bertalmio M,Sapiro G,Caselles V,et al. Image inpainting[C] //Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. NewYork,USA: ACM Press/Addison-Wesley Publishing Co.,2000: 417-424. |
| [2] | Chan T F,Shen J. Nontexture inpainting by curvature-driven diffusions[J]. Journal of Visual Communication and Image Representation,2001,12(4): 436-449. |
| [3] | Shen J,Chan T F. Mathematical models for local nontexture inpaintings[J]. SIAM Journal on Applied Mathematics,2002,62(3): 1019-1043. |
| [4] | Chan T F,Kang S H,Shen J. Euler's elastica and curvature-based inpainting[J]. SIAM Journal on Applied Mathematics,2002,62(1): 564-592. |
| [5] | Esedoglu S,Shen J. Digital inpainting based on the Mumford-Shah-Euler image model[J]. European Journal of Applied Mathematics,2002,13(4): 353-370. |
| [6] | Wong A,Orchard J. A nonlocal-means approach to exemplar-based inpainting[C] //15th IEEE International Conference on Image Processing. Piscataway,NJ,USA: IEEE,2008: 2600-2603. |
| [7] | 何凯,梁然,张涛. 基于小波系数相关性的纹理图像快速修复算法[J]. 天津大学学报,2010,43(12): 1093-1097. He K,Liang R,Zhang T. Fast texture image completion algorithm based on dependencies between wavelet coefficients[J]. Journal of Tianjin University,2010,43(12): 1093-1097. |
| [8] | 张平,檀结庆,何蕾. 基于离散小波变换的图像修补方法[J]. 计算机应用研究,2007,24(9): 287-289. Zhang P,Tan J Q,He L. Image inpainting method based on discrete wavelet transformation[J]. Application Research of Computers,2007,24(9): 287-289. |
| [9] | Han Y,Shi P. An adaptive level-selecting wavelet transform for texture defect detection[J]. Image and Vision Computing,2007,25(8): 1239-1248. |
| [10] | 王志鹏,张桂戌,基于分组行进算法的图像修补方法[J]. 中国图象图形学报,2007,12(5): 799-804. Wang Z P,Zhang G X,Digital image inpainting based on group marching method[J]. Journal of Image and Graphics,2007,12(5): 799-804. |
| [11] | 崔国庆,金波,张爱新. 基于KSVD与MCA的图像修复技术研究[J]. 通信技术,2013,24(1): 22-25. Cui G Q,Jin B,Zhang A X,Image Inpainting based on KSVD and MCA[J]. Communication Technology,2013,24(1): 22-25. |
| [12] | Liu J,Moulin P. Information-theoretic analysis of interscale and intrascale dependencies between image wavelet coefficients[J]. IEEE Transactions on Image Processing,2001,10(11): 1647-1658. |
| [13] | Shih T K,Tang N C,Hwang J N. Exemplar-based video inpainting without ghost shadow artifacts by maintaining temporal continuity[J]. IEEE Transactions on Circuits and Systems for Video Technology,2009,19(3): 347-360. |
| [14] | Duci A,Yezzi A J,Mitter S,et al. Region matching with missing parts[M] //Computer Vision-ECCV 2002. Berlin,Germnay: Springer,2002: 48-62. |
| [15] | 李开宇,孙玉刚. 引入连续性强度和置信度因子的快速图像修复[J]. 中国图象图形学报,2012,17(4): 465-470. Li K Y,Sun Y G,Fast image inpainting algorithm introducing continuous strength and confidence factor[J]. Journal of Image and Graphics,2012,17(4): 465-470. |
| [16] | Goyal P,Diwakar S. Fast and enhanced algorithm for exemplar based image inpainting[C] //2010 Fourth Pacific-Rim Symposium on Image and Video Technology. Piscataway,NJ,USA: IEEE,2010: 325-330. |



