2. 中国科学院大学, 北京 100049
2. University of the Chinese Academy of Sciences, Beijing 100049, China
1 引言
近年来随着定位技术的成熟以及定位设备的广泛应用，大量不同应用领域的移动终端产生了海量的轨迹数据，这些数据蕴涵着丰富的知识，能反映交通状态、 路网结构以及人们的移动规律等. 轨迹模式，可以被描述为个体或群体的移动对象在某一个时间段及某一个空间区域内的频繁移动行为. 它能够揭示移动对象的移动行为规律，能够反映与之相关的交通环境. 与之相关的研究成果可用于市政规划、 交通管理、 广告投放等方面的决策支持，也可以促进与LBS(location based services)等相关的新型移动应用的产生和发展. 比如，对城市车辆轨迹的频繁模式研究有助于了解市民的出行规律，能用于预测未来某一个时段某一条路线的交通状态. 再如，游人行程的频繁模式挖掘结果能用于揭示最热的旅游路线，而这可有助于商家营销方案的制定.
移动轨迹通常以GPS(global positioning system)定位点序列的形式存储和表示，比如T(p1，p2，…，pn)，那么轨迹频繁模式挖掘就可以借鉴传统的用于事务数据的序列模式挖掘方法[1, 2, 3]. 然而，由于现实中几乎不存在两个定位点完全一致的情况，而且很多定位设备都具有较高的采样率，会产生大量的冗余定位点，所以无法将传统序列模式挖掘算法直接应用于轨迹模式挖掘. 为此，可以将轨迹离散化，比如将轨迹所在区域划分为若干小区域，以定位点所处的小区域来标识轨迹，这样较长的定位点序列就转化为了较短的区域编号序列. 目前，关于轨迹离散化的研究已有不少，包括基于领域知识的划分方法、 基于网格的划分方法、 基于聚类的划分方法、 基于路网的划分方法.
第一种方法是使用相关的领域知识对区域进行划分，比如，可以根据详细的市政区域分划[4, 5]，将轨迹划归到不同的街区； 或者根据商圈、 车站等一些热点区域来划分轨迹. 这种方法可快速有效地划分轨迹，但通常情况下这类知识都是不可得的，所以此方法难以普遍适用.
第二种方法是将目标区域划分为m×n的规则网格[6, 7, 8, 9]，以轨迹点所处的网格离散化轨迹. 这种方法简便易行，但对算法网格大小敏感，且容易导致“模式丢失”的现象. 与此类似，文[10, 11]基于移动通讯网络中的基站覆盖范围为区域划分标准，这依然难以避免“模式丢失”，且通常基站覆盖范围都比较大，难以在结果中反映区域内的移动模式.
第三种是基于聚类的划分方法. 文[12, 13]则使用密度算法对轨迹点聚类，将点序列转化为聚类的编号序列. 文[14, 15, 16]提出了基于线段密度聚类的方法，将轨迹线段划分到不同的类簇，以聚类序列表示轨迹. 文[17]则使用网格聚类方法将区域聚类为若干不想重叠的矩形区域，以区域序列来表示轨迹. 这些方法能在保证其划分意义的前提下极大缩短序列长度，降低模式挖掘过程的复杂度. 但也存在一些不足，比如： 密度聚类方法的时间复杂度较高，每当数据发生变化时都需要重新聚类，无法反映大聚类区域内部的细致模式等.
第四种是基于路网匹配的划分方法[18, 19]. 它将车辆、 行人等移动受限的轨迹匹配到道路上，以道路序列表示轨迹. 此方法优点在于： 它既能极大缩减数据量，又能最大可能地保持移动模式的空间形状； 而且由于路网结构能长期稳定，避免了聚类划分方法的问题. 然而这种方式也有一定的弊端： 当使用整条路段表示短轨迹片段时会导致伪模式的产生； 且此类方法需要高精度路网拓扑的支持，而多数情况下高精度路网是难以获得的.
为解决路网匹配划分方法的这些问题，本文提出了一种基于路网探测的轨迹模式挖掘方法，本方法首先使用数学形态学从轨迹中探测出路网结构，而后基于道路匹配算法将轨迹离散化为“道路网格”序列(详见第2节)，进而使用最大序列模式挖掘方法进行轨迹模式挖掘.
本文主要贡献包括以下两点： 第一，提出了基于数学形态学构造路网结构的有效方法，设计了基于混合阈值的二值化方法，以及填补路网空隙的定向膨胀方法； 第二，提出了基于“道路网格”匹配的轨迹离散化方法，以解决传统离散方法所遇到的“模式丢失”问题等.
2 路网探测由于车辆等移动对象通常都沿着道路行驶，那么它们的轨迹也必能一定程度地反映道路的形状和拓扑结构，而且越靠近道路，轨迹也就越密集. 假若将地理区域划分为若干规则网格，并将每个小网格视为一个像素，将网格内的轨迹量视为像素值，那么位于道路之上的像素就一定较高. 基于这样的事实，就可以使用图像处理方法剔除掉灰度值较低的像素，保留道路上的灰度值较高的像素，从而也就提取到了路网的轮廓.
本研究的路网探测过程主要包括3个步骤： 首先，将包含有大量轨迹的二维空间区域构造为位图图像，然后对位图进行二值化，最后使用数学形态学中的薄化、 腐蚀、 裁剪等操作从二值图像中提取路网结构.
2.1 构造位图定义1 轨迹位图： 给定一个地理区域S，按照经纬度方向将其分别划分为m、 n等分(m>0，n>0)，即将区域S划分为m×n个矩形网格单元，若将每个网格视为一个像素，则S可表示为位图Gbit=｛g1，g2，…，gm×n｝，每个像素的灰度值Gray即为通过该网格的轨迹量，G(gi)≥0，i>0.
方便起见，下文中将覆盖在道路上的网格称为“道路网格”，不覆盖道路的网格称为“非道路网格”，与它们相对应的像素分别称为“道路像素”和“非道路像素”.
2.2 位图二值化二值化过程是使用阈值对灰度图进行过滤，将其转化为二值图像. 其目的是删除“非道路网格”，保留“道路网格”.
二值化的关键问题是如何选择阈值. 最简单的办法是人为选定一个全局阈值，但全局阈值的通用性很差，当阈值较大时会导致只包含少量轨迹的“道路网格”被误删，致使最后的路网只能包含高流量的道路； 而当阈值较小时会导致包含有较多轨迹的“非道路网格”被误留，甚至将多条不同路段“粘”到一起. 避免此问题的一种有效策略是使用局部阈值，即根据局部区域信息确定可适应的阈值. 然而局部阈值也可能会出现问题，当某一区域内不包含道路却有少量轨迹时，使用局部阈值就可能将“非道路网格”被错误地保留.
不失一般性，“道路像素”的灰度值通常大于“非道路像素”的灰度值，那么使用局部非0像素的平均值就能过滤掉“非道路像素”. 同样，使用全局非0像素的平均值就能过滤掉被局部均值保留下来的伪“道路像素”. 鉴于此，本文采用一种同时使用全局均值和局部均值的混合阈值策略. 设Aglobal为全局非0像素的平均值，Aγ×γ(g)为像素g的γ×γ邻域内的非0像素平均值，那么像素g的过滤阈值可以定义为
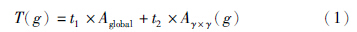
经过二值化处理后，图像将只包含邻近道路的网格，即结果图像将能显示出路网的轮廓. 然而，二值化操作也将不可避免地导致结果图像中出现“空洞”、 “裂缝”、 “肿块”等现象. “空洞”、 “裂缝”会使原本相连的道路产生断裂，而“肿块”将会使原本相距甚远的道路变得相邻，甚至将它们“粘”到一起. 为了填补道路间隙、 平滑边缘，可以使用数学形态学中的膨胀、 桥接等操作； 而要消除“肿块”，这就可以使用腐蚀或细化操作.
2.3.1 细化细化操作是将二值图像简化为单像素相连的图像，它能保持图像连通性不变. 细化操作通常可以使用形态学中的击中/击不中变换来定义：
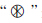表示击中/击不中变换，
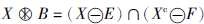. 细化操作的更一般的表达是利用结构元素序列B1，B2，…，Bn迭代对图像X进行处理，直至X不再变化为止：
 |
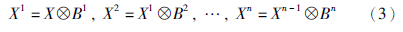
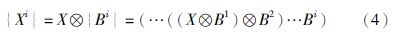
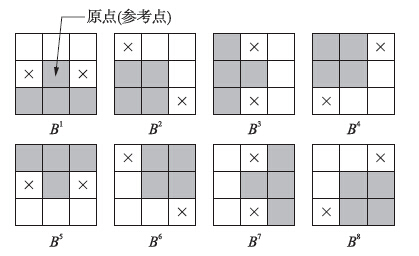| 图 1 细化操作中的结构元素序列Fig. 1 Structural elements sequence in thinning operation |
经过细化处理后，二值图像成为了路网的骨架结构. 然而，依然存在许多断裂需要进一步处理. 这里我们使用膨胀操作填补道路间隙. 膨胀操作定义如下：
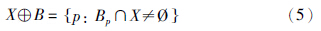
通常，膨胀操作的结构元素都选用3×3或5×5的对称结构，然而这里却不能对全部像素都使用一种固定的结构元素. 因为，每条道路要么是单向要么是双向，那么对“道路像素”作膨胀处理时就只能朝着道路的一个或两个方向进行. 比如，对于一个位于东西向双行道上的像素p，它的结构元素就应该是水平的1×3或1×5结构； 同样，对于南北双行道路上的像素而言，其结构元素就可以是垂直的3×1或5×1结构. 从这个意义上说，每个道路像素都应该有属于自己的结构元素. 这个问题并不复杂，通过统计每个网格内的车辆行驶方向就可以方便地确定相应像素的结构元素.
2.3.3 裁剪细化算法所求得的骨架会产生一些毛刺噪声，经过上节的定向膨胀处理之后噪声会更加严重，所以需要通过裁剪去掉这些无用的部分. 裁剪操作是细化操作的一种变体，可以通过细化操作来定义，不同之处在于，对图像连续裁剪不能达到一种稳定状态，它有可能消去整个图像. 这里我们采用图 2所示的8个结构元素，其中B1～B4为4个强修剪器，B5～B8为4个弱修剪器.
 |
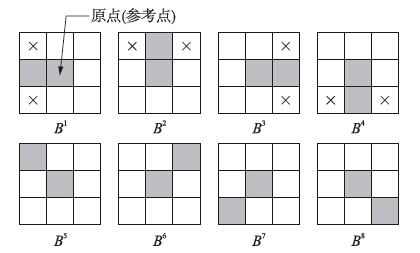| 图 2 裁剪操作中的结构元素序列Fig. 2 Structural elements sequence in pruning operation< |
经过上面的形态学处理之后，二值图像就可以视为一幅路网地图.
定义2 路网： 给定轨迹位图Gbit，对其执行二值化和形态学处理之后，结果图像就可以表示为一个路网Groad=｛g1′，g2′，…，gi′，…｝，i∈(1，m×n］，gi′≠gj′，gi′=gk，i≠j，k>0，G(gi′)=1，1≤N(gi′)≤4，GroadGbit，其中N(gi′)表示网格gi′在路网Gbit中的直接邻接网格.
算法1 列出了基于形态学的路网探测过程，设GPS定位点数量为p，网格数量为n，图像处理的迭代次数为k，那么算法复杂度为O(p+n×k).
| 算法1 Road network(S，T，m，n) |
| 输入： 地理空间S，轨迹集合T，网格行数m，网格列数n 输出： Road network Groad 1. //将空间S划分为m×n的规则网格Gbit，并将T映射到Gbit中 2. Gbit←｛g1，g2，…，gm×n｝； 3. for each(g∈Gbit)｛ 4. //根据式(1)计算Gbit中每个网格的过滤阈值T 5. T(g)←t1×Aglobal+t2×Aγ×γ(g)； 6. ｝ 7. 使T将Gbit转化为二值图像； 8. for each(g∈Gbit)｛ 9. //为Gbit中的所有像素构造结构元素数组M 10. 通过检测网格g内的车辆行驶方向确定像素g的膨胀方向d； 11. 为像素g构造结构元素Mg； 12.｝ 13.Groad←Morphology(Gbit，M)； //使用细化、 膨胀、 剪枝等形态学操作构造路网 14.Return Groad； |
获得路网之后即可将轨迹匹配到道路上，以“道路网格”序列作为轨迹的离散化表示. 关于道路匹配算法已有不少研究[20, 21, 22, 23, 24]. 然而，由于我们的路网结构简单，不存在车道、 环岛、 立交桥等复杂道路结构，所以只需使用简单的匹配方法即可，即通过距离计算将轨迹匹配到一定邻域γ内距离最近的“道路网格”中. 对于每一个轨迹点p，若其所在的网格g是路网的一部分，则p直接匹配到gi中； 若gi不包含在路网中，则在gi的γ邻域内的网格中寻找距离p最近的“道路网格”gj，将p匹配到gj中； 若γ邻域内不存在“道路网格”，则将p视为噪声点.
定义3 道路匹配： 给定一个轨迹点p，以及路网Groad，p到Groad的匹配定义为
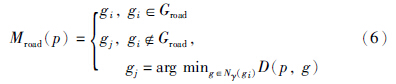
当轨迹转化为网格序列时，便可使用传统序列模式挖掘算法对轨迹进行处理. 然而由于网格宽度较小会导致网格序列较长，比如，当网格宽度为50 m时，一条2 km长的轨迹将由40个网格组成. 这样将直接导致挖掘到的频繁序列数量十分庞大，显然这会极大增加计算代价. 对于轨迹模式而言，很多短小的模式是无意义的，因为我们通常只需关注最长的频繁轨迹模式. 如图 3所示，由于模式4包含了模式1、 2、 3，那么只需知道模式4即可，另外3个冗余模式的存在不但没有太大意义，反而加大理解的困难. 针对轨迹模式的这种特性，可以使用最大频繁序列模式挖掘方法来解决. 其优点在于： 最大频繁序列已经隐含了所有频繁序列，因此前者的数量要比后者小很多，且从一个最大频繁序列中可以方便地推导出其所包含的频繁子序列. 本文采用MaxSequence算法[25]挖掘最大频繁轨迹模式. 图 4给出了本文算法的总体流程图，包括路网探测、 道路匹配及模式挖掘.
 |
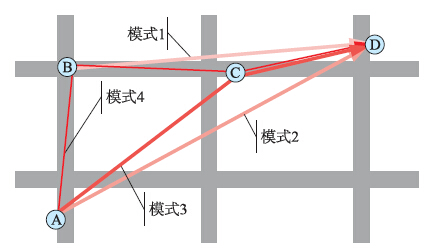| 图 3 轨迹模式中的最大频繁模式Fig. 3 Maximal frequent pattern in trajectory patterns |
 |
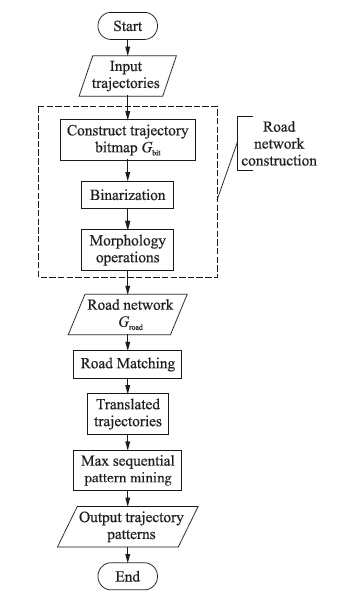| 图 4 本文算法总体流程图Fig. 4 The flow chart of the proposed algorithm |
本文算法均在Windows XP平台下使用C＃语言实现，实验平台为Intel Core Duo 2 E7400 CPU，2 G内存.
5.1 实验数据实验中所用的数据为深圳市13 798辆出租车3 h的历史轨迹，共包括2 448 245个GPS定位点，取样间隔不固定，在30 s～60 s之间.
出租车轨迹包括两部分，其一为载客轨迹，即从上客点到下客点之间的轨迹； 其二为空载轨迹. 由于本文的目的是挖掘频繁的轨迹模式，探索人们的出行规律，而只有载客轨迹才能更好地满足这个需求，所以我们只使用前者进行轨迹模式挖掘，且使用全部数据进行路网探测. 利用载客状态的变化，我们从数据集中分离出94 824条载客轨迹.
5.2 参数设定路网探测算法中的位图构造部分有2个参数： 横向等分数m和纵向等分数n. 它们的大小应根据地理范围的大小以及道路宽度来设定，通常一个网格的长和宽应小于大多数道路的宽度，这样才能保证一个网格不会覆盖多条道路且包含于道路之中(能代表道路的脊线). 另外，网格长宽应保证尽可能相等，这样有利于图像处理. 根据常识，网格宽度在10 m～50 m之间是合理的. 本实验中采用50 m宽度.
位图二值化部分中的式(1)也包括2个参数： 全局均值权重t1和局部均值权重t2，t1通常不应大于t2，不然，过滤像素时将过多地受全局均值的影响，从而导致“道路网格”的误删. 以下实验将对此两个参数的设定进行探讨.
5.3 结果分析 5.3.1 路网探测结果为了展示路网探测算法的有效性，下面对不同参数的实验结果作对比. 由于缺乏实际路网的精确矢量数据做基准，我们无法对探测的路网精度作量化分析，这里只与实际路网结构作直观性对比. 本节的图例中，灰色线条为实际路网图，黑色线条为探测到的路网.
首先，对二值化过程中式(1)的不同权值组合作对比分析，如图 5所示，当只使用全局阈值时(图 5(a))，只有一部分道路被识别出来； 而随着局部阈值的权重逐渐增大，被识别出的道路越来越多. 这也就印证了2.2节中的说法，即t1不应大于t2. 同时也表明了本文提出的混合阈值策略的有效性.
 |
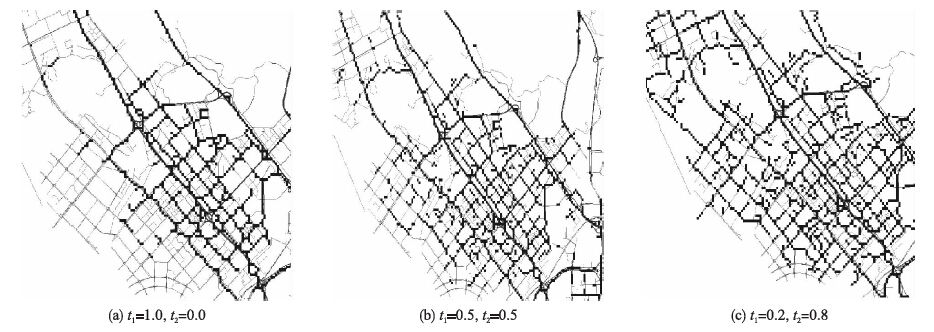| 图 5 二值化过程中不同权值的结果对比Fig. 5 Comparison of different weights in binarization |
其次，对比不同结构元素对膨胀操作产生的影响. 如图 6所示，使用3×3结构的结构元素对二值图像作膨胀处理后，导致很多道路粘到了一起(图 6(a))； 而使用2.3.2节中提出的定向性结构元素对二值图像作膨胀处理后，即使相距很近的道路也能被区分开(图 6(b)). 由此可见，本文提出的定向性膨胀策略十分有效.
 |
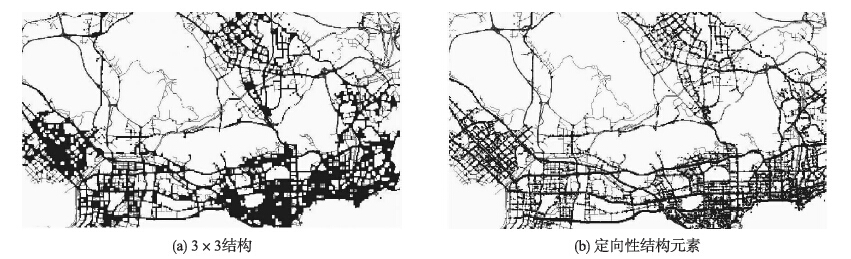| 图 6 不同结构元素对膨胀操作的影响Fig. 6 Comparison of different structural elements in dilation operation |
经过形态学处理后的路网结构如图 7所示，由图中可以看出，除了一些偏僻小路之外，绝大部分主要道路都被识别出来了. 因为偏僻小路上经过的车辆很少，而较少的轨迹不会具备频繁模式的特征，所以这些未被识别出的小路也不会对轨迹模式挖掘结果产生影响. 同时，若要提高路网的识别率，只需使用更多轨迹即可.
 |
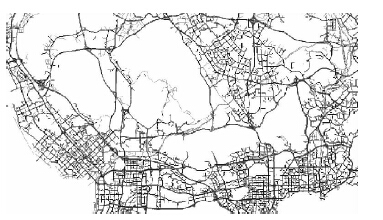| 图 7 最终的路网结构Fig. 7 Final road network |
为了展示本文算法能探测到更多更细致的轨迹模式，这里与基于网格划分的算法、 基于聚类的算法(PopularRegions)[17]进行对比.
图 8展示的是这三种算法的轨迹模式挖掘结果. 由图中可看出，本文提出的基于路网探测及道路匹配的挖掘算法能够探测很多较长的轨迹模式，且这些模式均能与道路形状保持高度一致(图 8(a))； 而基于简单网格划分的算法只能探测到一些较短的轨迹模式(图 8(b)). 图 9为两者的模式长度及数量对比，从中可以更清楚地看出前者比后者能探测到更多长模式(模式长度是指每个模式所包含的网格个数). 究其原因，是因为道路匹配能将道路附近的轨迹都“集中”到道路脊线上的网格中，从而克服了网格硬划分方法将属于同一条道路的多条轨迹划分到不同网格中的错误现象，最终使得更多长轨迹序列满足了模式支持度阈值.
 |
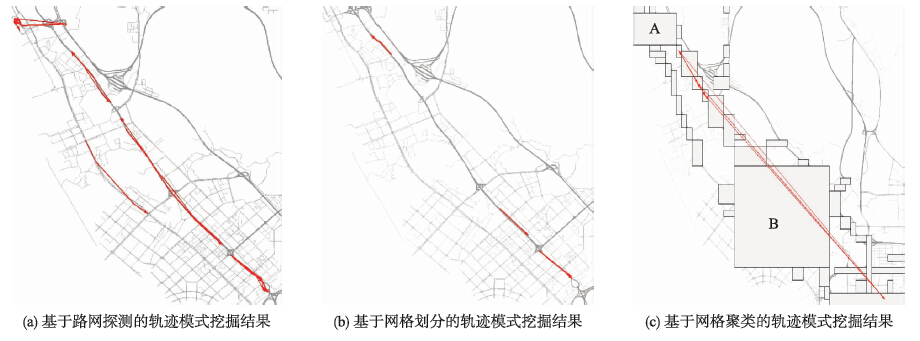| 图 8 三种轨迹模式挖掘算法的结果对比Fig. 8 Comparison of three trajectory pattern mining algorithms |
 |
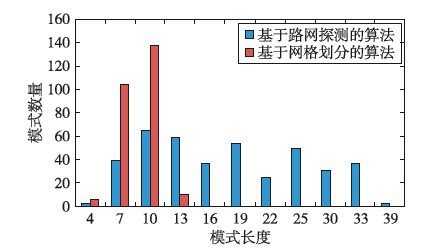| 图 9 基于路网探测的算法与基于网格划分算法的轨迹模式数量对比Fig. 9 Quantity comparison of trajectory patterns between road network detecting-based algorithm and grid splitting-based algorithm |
由图 8(c)可看出，道路稠密的区域由于轨迹较多，所形成的聚类就较大，如区域A、 B； 而道路稀疏的区域由于轨迹量小，所形成的聚类也就较小，这些小聚类区域主要沿着道路分布. 这样，最终的轨迹模式只能反映轨迹在某些大区域之间的移动规律，而无法反映大聚类区域内部的轨迹模式，也难以反映其它小聚类区域之间的轨迹模式. 由此表明，与基于聚类的算法相比，本文算法能够探测出更细致的轨迹模式. 5.3.3 路网精度的影响
由于对轨迹离散化所使用的路网也是从轨迹中提取出来的，那么轨迹的道路匹配结果一定会受路网精度的影响. 轨迹量越大所构造的路网覆盖度就一定越高，轨迹的道路匹配精度也一定越高. 经实验发现，当使用的轨迹超过2 h时，所构造的路网便能覆盖绝大部分实际道路，而探测到的轨迹模式也基本能保持稳定. 图 10显示了3 h轨迹在2 h路网和3 h路网中所探测到模式数量对比，从中可看出使用二者探测到的轨迹模式数量没有太大差别，微小的不同在于前者探测的短模式稍多些，而后者探测的长模式更多些.
 |
| 图 10 基于不同路网探测出的轨迹模式数量Fig. 10 Quantity comparison of trajectory patterns based on different road networks |
这里讨论路网构造算法的执行效率. 由图 11中可看出，随着数据量的增加，算法的运行时间几乎呈线性增加. 而且，当定位点数量达到2.4×106时，算法执行时间也没超过3 min(包括读取数据文件的时间). 这表明了此算法效率较高.
 |
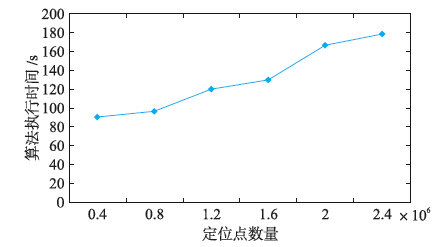| 图 11 路网构造算法的效率Fig. 11 Efficiency of road network construction algorithm |
另外需要说明的是，由于路网本身的稳定性，一旦路网构造完毕就可以一直被使用，而无需在每次探测轨迹模式时都先执行一遍路网构造算法. 从这一点上讲，在进行多次轨迹模式挖掘时路网构造算法的计算代价可以忽略不计.
6 总结本文研究了轨迹模式挖掘过程中的轨迹离散化问题，针对移动受限轨迹提出了基于路网匹配的轨迹离散化解决方案. 为此，实现了基于形态学方法从轨迹中提取路网的算法. 经实验表明，此算法能够快速构造出高覆盖率的路网. 通过道路匹配的方式对轨迹进行离散化之后，利用最大频繁序列模式挖掘算法就能有效地探测出轨迹模式. 经实验对比，证明了基于道路匹配的算法克服了简单网格划分造成的“模式丢失”现象，同时也解决了基于聚类的算法无法探测聚类内部移动模式的问题.
| [1] | Han J W,Pei J,Mortazavi-Asl B,et al. FreeSpan: Frequent pattern-projected sequential pattern mining[C] //Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York,NJ,USA: ACM,2000: 355-359. |
| [2] | Pei J,Han J W,Mortazavi-Asl B,et al. Prefixspan: Mining sequential patterns efficiently by prefix-projected pattern growth[C] //Proceedings of the 17th International Conference on Data Engineering. Piscataway,NJ,USA: IEEE,2001: 215-224. |
| [3] | Zaki M J. SPADE: An efficient algorithm for mining frequent sequences[J]. Machine Learning,2001,42(1): 31-60. |
| [4] | Yue Y,Wang H D,Hu B,et al. Exploratory calibration of a spatial interaction model using taxi GPS trajectories[J]. Computers,Environment and Urban Systems,2012,36(1): 140-153. |
| [5] | Yue Y,Zhuang Y,Li Q Q,et al. Mining time-dependent attractive areas and movement patterns from taxi trajectory data[C] //2009 17th International Conference on Geoinformatics. Piscataway,NJ,USA: IEEE,2009: 1-6. |
| [6] | Wei L Y,Zheng Y,Peng W C. Constructing popular routes from uncertain trajectories[C] //Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York,USA: ACM,2012: 195-203. |
| [7] | Wang L,Hu K Y,Ku T,et al. Mining frequent trajectory pattern based on vague space partition[J]. Knowledge-Based Systems,2013,50(1): 100-111. |
| [8] | Veloso M,Phithakkitnukoon S,Bento C. Urban mobility study using taxi traces[C] //Proceedings of the 2011 International Workshop on Trajectory Data Mining and Analysis. Piscataway,NJ,USA: IEEE,2011: 23-30. |
| [9] | Gidófalvi G,Pedersen T B. Mining long,sharable patterns in trajectories of moving objects[J]. GeoInformatica,2009,13(1): 27-55. |
| [10] | Yavas G,Dimitrios K,Özgür U,et al. A data mining approach for location prediction in mobile environments[J]. Data & Knowledge Engineering,2005,54(1): 121-146. |
| [11] | Sohn K,Kim D. Dynamic origin-destination flow estimation using cellular communication system[J]. IEEE Transactions on Vehicular Technology,2008,57(5): 2703-2713. |
| [12] | Cao H P,Mamoulis N,Cheung D W. Discovery of periodic patterns in spatiotemporal sequences[J]. IEEE Transactions on Knowledge and Data Engineering,2007,19(4): 453-467. |
| [13] | Giannotti F,Naani M,Pedreschi D,et al. Trajectory pattern mining[C] //International Symposium on Computing with Spatial Trajectories. Berlin,Germany: Springer,2011: 143-177. |
| [14] | Cao H P,Mamoulis N,Cheung D W. Mining frequent spatio-temporal sequential patterns[C] //Fifth IEEE International Conference on the Data Mining. Piscataway,NJ,USA: IEEE,2005. |
| [15] | Chen G,Chen B Q,Yu Z Z. Mining frequent trajectory patterns from GPS tracks[C] //2010 International Conference on the Computational Intelligence and Software Engineering. Piscataway,NJ,USA: IEEE,2010: 1-6. |
| [16] | Kang J,Yong H S. Mining spatio-temporal patterns in trajectory data[J]. JIPS,2010,6(2): 521-536. |
| [17] | Giannotti F,Naani M,Pedreschi D,et al. Trajectory pattern mining[C] //Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York,USA: ACM,2007. |
| [18] | Li X L,Han J W,Lee J G,et al. Traffic density-based discovery of hot routes in road networks[C] //10th International Symposium on Advances in Spatial and Temporal Databases. Berlin,Germany: Springer,2007: 441-459. |
| [19] | Won J I,Kim S W,Baek J H,et al. Trajectory clustering in road network environment[C] //IEEE Symposium on Computational Intelligence and Data Mining. Piscataway,NJ,USA: IEEE,2009: 299-305. |
| [20] | Lou Y,Zhang C Y,Zheng Y,et al. Map-matching for low-sampling-rate GPS trajectories[C] //Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York,USA: ACM,2009: 352-361. |
| [21] | Goh C Y,Dauwels J,Mitrovic N,et al. Online map-matching based on hidden markov model for real-time traffic sensing applications[C] //2012 15th International IEEE Conference on Intelligent Transportation Systems. Piscataway,NJ,USA: IEEE,2012: 776-781. |
| [22] | Miwa T, Kiuchi D, Yamamoto T, et al. Development of map matching algorithm for low frequency probe data[J]. Transportation Research Part C: Emerging Technologies, 2012, 22(1): 132-145. |
| [23] | Hunter T, Abbeel P, Bayen A M, et al. The path inference filter: Model-based low-latency map matching of probe vehicle data[C]//Proceedings of the 10th International Workshop on the Algorithmic Foundations of Robotics. Berlin, Germnay: Springer, 2013: 591-607. |
| [24] | Chen D, Driemel A, Guibas L J, et al. Approximate map matching with respect to the Fréchet distance[C]//Proceedings of the Workshop on Algorithm Engineering and Experiments. Berlin, Germany: Springer, 2011: 75-83. |
| [25] | Afshar R. Mining frequent max and closed sequential patterns[D]. Vancouver, Canada: Simon Fraser University, 2002. |