1 引言
间歇过程存在非线性特性和扰动问题,控制器设计时模型存在不确定性,且在实际运行时也有输入输出约束问题. 控制器若采用比例—积分—微分控制,往往和参考轨迹有一定的误差,且从控制系统时域分析,上升时间比较长. 这引起了学者的广泛关注[1, 2, 3, 4, 5, 6]. 为了快速跟踪给定参考轨迹,需采用先进的控制方法设计控制器跟踪参考轨迹. 因此近些年来,迭代学习控制(iterative learning control,ILC)算法被广泛应用于间歇过程中的跟踪控制问题. ILC的基本原理是利用前面批次过程的历史数据来提高当前批次系统性能.
对间歇过程的控制,国内学者Xiong[7]提出了基于时变偏扰模型表示间歇过程,采用迭代学习控制跟踪给定的期望轨迹,同时文[8]对间歇过程的控制做出了较详细的综述. 将预测控制运用在间歇过程中,可从不同的角度考虑,分别为末端点控制[9]和轨迹控制[10]. 但这是从一个批次角度考虑间歇过程重复性的运行过程,故引入2维技术,Shi[11, 12, 13, 14]等提出将2D(two dimensional)控制系统用在间歇过程的控制中. 2D系统指构建的综合系统不仅有时间变量而且还有批次变量,文章中主要解决了间歇过程中的不确定参数和初始值不确定性问题,但控制算法中未考虑输入输出约束问题. 线性矩阵不等式(LMI)有较强的约束能力,将不确定系统的预测控制技术[15],推广到2D系统,即基于2D系统的重复控制[16],针对2D系统采用了2D李亚普诺夫函数构建了基于模型预测控制的LMI,通过求解LMI问题保证了重复控制系统沿周期和时间方向收敛. 文[17, 18, 19]对间歇过程不确定时延和故障容错作出一定研究,巩固了间歇过程的应用. Liu[20]对非线性间歇过程在不同平衡点处线性化为仿射线性系统,转化为2D系统时采用状态反馈和输出反馈设计鲁棒控制律,对参考轨迹进行跟踪.
本文主要针对非线性间歇过程,在平衡点处线性化,得到线性状态空间方程. 考虑2维系统优势,将简化的状态空间模型转化为2D Rosser系统,采用预测控制算法并给出适合2D性能的优化指标,同时将优化问题转化为凸优化问题,进而通过求解上述LMI不等式得到下一时刻的系统输入. 在下一批次运行时,将上一批次的输入作为参考量,结合当前的预测控制给出更新律,再将控制律代入到系统运行. 数值仿真结果验证了该设计控制算法的有效性.
2 问题描述2.1 非线性间歇过程的描述
考虑下面非线性间歇过程:
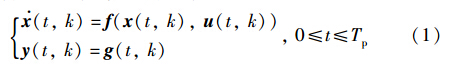
其中,x(t,k)∈ R n,u(t,k)∈ R m,y(t,k)∈ R p,t表示时间,k代表批次,T p 是系统每周期运行的时间,x(0,k)表示系统各批次的初始状态.
间歇过程产品的质量往往和过程状态变量有关,比如CSTR中温度常常是一个重要变量. 如果温度控制的精度高,那么间歇过程的产品质量就高. 设定参考轨迹常常是由经验或者通过最优控制求解式(1)获得. 针对上述非线性方程(1),需要线性化处理. 本文采用泰勒展开法在某一平衡点(xeq,ueq)处线性化非线性方程:
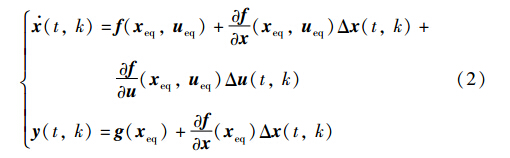
由于现代采集技术都是通过计算机实现的,最终的表现都是离散的数据,因此将上面的连续系统简化为下面离散方程. 以式(3)模型为基础设计控制算法,使得式(1)能够跟踪参考轨迹.
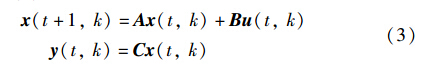
2.2 2D Rosser模型
为便于表述2D Rosser模型,定义函数如下:
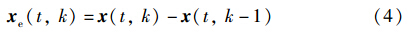
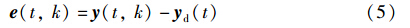
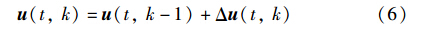
其中x e (t,k)为系统状态批次误差,e(t,k)为系统误差, Δ u(t,k)是系统输入的更新律,u(t,k)是通过前一批次的输入和当前批次的增量叠加得到的,这种控制律形式被称为迭代学习控制律.
结合式(3)~(6)可得到下面的状态方程:
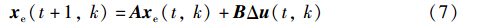
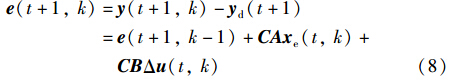
将式(7)、 (8)综合在一个框架内,得到等价的2D系统模型:
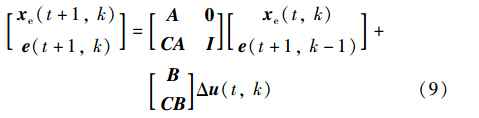
对于系统(9)采用迭代学习控制律(6),其中迭代学习控制律的具体表现形式如下:

将式(10)代入到式(9)得到下面的2D Rosser状态空间模型:
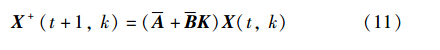
其中 =A0CAI,=BCB X+(t+1,k)=x Te (t+1,k)e Τ (t+1,k) Τ X(t+1,k)=[x Te (t,k) e Τ (t+1,k-1)] Τ
下面将对系统(11),设计控制器使得系统(11)鲁棒稳定.
3 2D鲁棒预测控制设计文[7]对1维系统提出了基于LMI的鲁棒预测控制,现将此方法拓展到2D系统中,使得系统(1)不仅能够收敛而且还满足给定的输入输出约束.
间歇过程被要求每一批次都跟踪给定的参考轨迹同时满足输入输出约束. 利用以前批次的稳定状态信息设计控制器,可以在每一批次k和每一时刻t优化下面的性能指标:

其中控制域和预测域为N-t-1,N-t-1表示优化指标的时间段,y((t+i+1)|t,k)是k批次t+i+1时刻的预测值. 可以看出性能指标函数是最小化当前批次剩下时间的输出误差且预测域和时间域从当前批次看是随时间的运行不断地减小.
结合式(11),目标函数(12)可以转换为
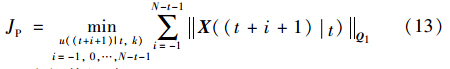
其中Q1为权值矩阵.
3.1 控制器设计和稳定性这部分利用2D李亚普诺夫函数证明系统的稳定性,并且推导出控制器增益 K . 定义李亚普诺夫函数:
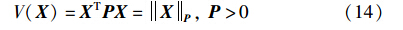
为了证明2D系统的稳定性,假设系统(11)满足2D李亚普诺夫函数不等式约束:
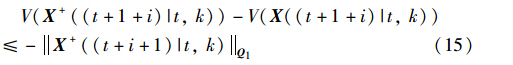
对i进行如下形式的求和:

可以得到:
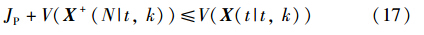
上式给出了性能指标的上限.
最小化V(X(t|t,k)),等价于最小化:
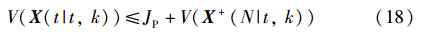
为了使上面的不等式成立,且前一批次的信息已经确定,故假设下面约束条件成立:
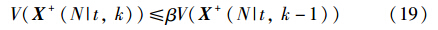
则式(18)可以写成:
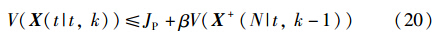
由于X+(N|t,k-1)的信息已经确定且在第k批次保持恒定,定义V(X+(N|t,k-1))=M. 即若式(20)成立,则不等式(15)成立,由此可以推出系统是稳定的.
下面求解控制器增益K.
定理1 系统在批次运行时是渐近稳定的,存在变量λ>0、 β>0和适当的矩阵Q、 Y可使得下面的矩阵不等式成立:
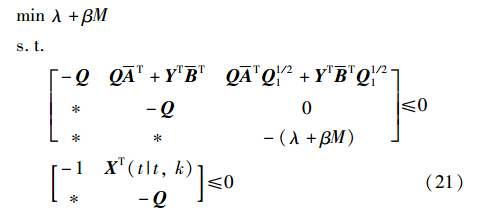
其中P和Y是 LMI 的解,Y=KQ,Q=(λ+βM)P-1.
证明 最小化V(X(t|t,k)),则不等式(20)等价于:
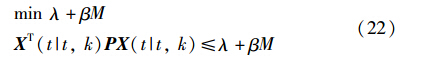
定义Q=(λ+βM)P-1,则式(20)等价于不等式:
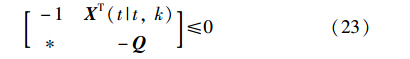
将式(11)代入式(15)得到:
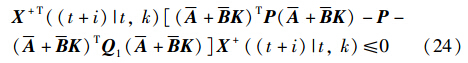
即对于所有的i,下面的不等式成立:
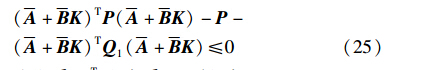
对上式两边左乘Q T 和右乘Q ,得到:
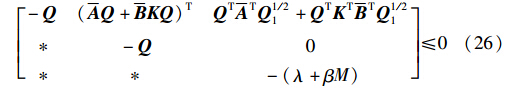
令Y=KQ,则式(26)可以写成:

3.2 约束问题处理
当系统存在较大误差或者较大扰动时,会使得系统的输入值较大,而这些控制作用从安全角度和实际物理限制等实际情况看是不允许的,系统的性能会变差甚至导致系统不稳定. 因此考虑系统的输入输出约束问题在实际过程中是非常重要的,由式(23)可知:

3.2.1 输入约束
下面将考虑2D Rosser模型的输入输出约束问题转换为求解LMI问题. 若输入满足如下2范数:
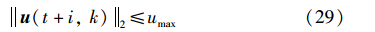
则将定理1中控制作用代入式(29)可得到:
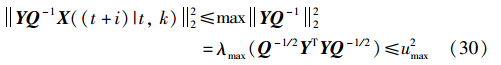
将式(30)转化为下面的不等式:
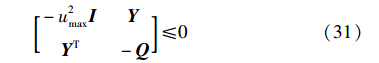
3.2.2 输出约束
下面将2D Rosser模型的输出约束问题转化为LMI问题. 若输出满足如下2范数约束条件:
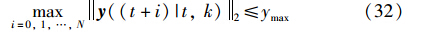
则
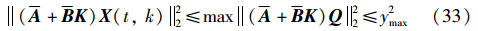
即为

3.3 控制算法流程图
系统(1)在实施鲁棒预测控制策略前应初始化,包括批次运行周期的输入输出值、 系统的参考轨迹、 模型简化、 系统的初始值. 控制流程图如图 1所示.
 |
| 图 1 控制流程图Fig. 1 The flow chart of control |
将上述算法用控制框图表示如图 2所示,图中虚线表示的是上一批次的信息,实线表示当前批次的信息.
 |
| 图 2 控制结构Fig. 2 Control structure |
4 仿真实例
4.1 仿真模型
考虑具有较强非线性的连续搅拌釜反应. 反应过程如图 3所示.
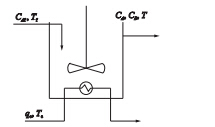 |
| 图 3 传统CSTR框图Fig. 3 Typical CSTR chart |
这是一个恒定体积、 发热、 不可逆反应,A→B. 从物料平衡和热量平衡反应角度可得到反应方程的机理模型如式(35)所示:
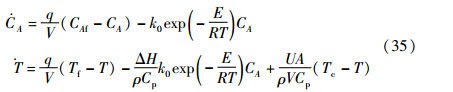
系统参数值如表 1所示.
| 参数 | 值 | 备注 |
| q | 100 L/min | |
| V | 100 L | |
| CA f | 1 mol/L | |
| T f | 400 K | |
| ρ | 1 000 g/L | |
| C p | 1 J/(g·K) | |
| k0 | 4.71×108 min-1 | |
| E/R | 8 000 K | |
| Δ H | -2×105 J/mol | |
| UA | 1×105 J/(min·K) | 约束条件: 200≤ T c≤450 K 0≤ CA ≤1 mol/L 250≤ T ≤500 K |
模型中的两个状态变量: CA为反应器中A的浓度,T是反应器中的温度. 操作变量T c 是夹套中的温度. 设初始状态(C eq ,T eq )=(0.898 6,361.141),T c=302 K,且每一批次初始状态保持不变. 经过10 min反应后,期望反应器最终的状态量为( C eq, T eq)=(0.52,398.972). 如果从批次运行角度看,此过程则可看成间歇过程. 给定温度参考轨迹,使得在线温度能够跟踪参考轨迹. 可将上述基于2D模型的预测控制算法运用于跟踪参考轨迹.
根据文[9]将易于测量的状态变量温度作为参考轨迹:

4.2 仿真结果
无扰动的情况:

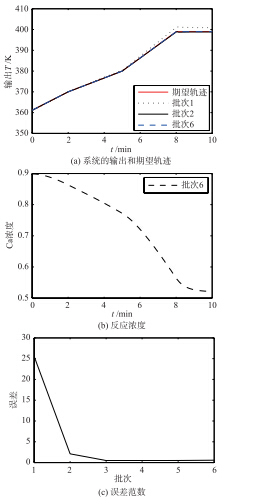 |
| 图 4 系统温度输出、 浓度、 绝对误差图(无扰动)Fig. 4 The system′s temperature output,concentration,absolute error without disturbance |
有重复扰动的情况:
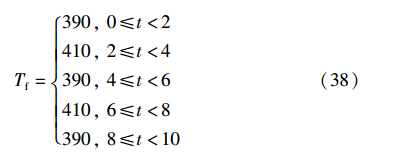
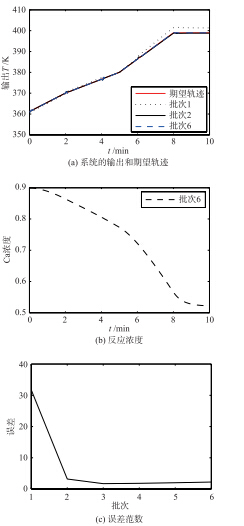 |
| 图 5 系统温度输出、 浓度、 绝对误差图(重复扰动)Fig. 5 The system′s temperature output,concentration,absolute error with repetitive disturbance |
扰动不确定的情况:

从图 4~6给出的3种扰动情况可以看出,本文所设计的控制器在面对不确定扰动的情况时,可以跟踪系统的参考轨迹. 各个批次随机的非重复性扰动和各个批次重复性扰动相比,非重复性扰动下的系统绝对误差较大,是由于系统的输出要完全跟踪系统的期望轨迹,需要系统可逆,这条件约束性极强,对非线性系统而言条件更为苛刻,因此只要系统的期望轨迹渐近跟踪期望轨迹即可.
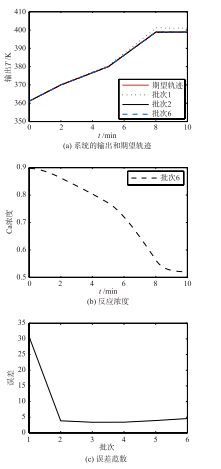 |
| 图 6 系统温度输出、 浓度、 绝对误差图(不确定扰动)Fig. 6 The system′s temperature output,concentration,absolute error with uncertainty disturbance |
5 结语
针对间歇过程中的非线性和输入输出约束问题,通过2D鲁棒预测控制算法将上述问题转化为LMI问题,同时给出了控制算法的稳定性证明,指出了系统在批次和时间方向上的收敛性. 将控制算法用在对间歇反应器温度参考轨迹的跟踪上,仿真结果表明设计的控制算法在无扰动、 重复性扰动和非重复性扰动情况下能够实现对参考轨迹的跟踪控制.
| [1] | Bonvin D. Control and optimization of batch processes[J]. IEEE Control Systems, 2006, 26(6): 34-45. |
| [2] | Lee J H, Lee K S. Iterative learning control applied to batch processes: An overview[J]. Control Engineering Practice, 2007, 15(10): 1306-1318. |
| [3] | Lee J H, Lee K S, Kim W C. Model-based iterative learning control with a quadratic criterion for time-varying linear systems[J]. Automatica, 2000, 36(5): 641-657. |
| [4] | Ahn H, Lee K S, Kim M, et al. Control of a reactive batch distillation process using an iterative learning technique[J]. Korean Journal of Chemical Engineering, 2014, 31(1): 6-11. |
| [5] | Chin I, Qin S J, Lee K S, et al. A two-stage iterative learning control technique combined with real-time feedback for independent disturbance rejection[J]. Automatica, 2004, 40(11): 1913-1922. |
| [6] | Lee K S, Lee J H. Iterative learning control-based batch process control technique for integrated control of end product properties and transient profiles of process variables[J]. Journal of Process Control, 2003, 13(7): 607-621. |
| [6] | Lee K S, Lee J H. Iterative learning control-based batch process control technique for integrated control of end product properties and transient profiles of process variables[J]. Journal of Process Control, 2003, 13(7): 607-621. |
| [8] | Wang Y, Gao F, Doyle III F J. Survey on iterative learning control, repetitive control, and run-to-run control[J]. Journal of Process Control, 2009, 19(10): 1589-1600. |
| [9] | Lee K S, Chin I S, Lee H J, et al. Model predictive control technique combined with iterative learning for batch processes[J]. AIChE Journal, 1999, 45(10): 2175-2187. |
| [10] | Ghaffari V, Naghavi S V, Safavi A A. Robust model predictive control of a class of uncertain nonlinear systems with application to typical CSTR problems[J]. Journal of Process Control, 2013, 23(4): 493-499. |
| [11] | 师佳, 江青茵, 曹志凯, 等. 一种基于2维鲁棒预测控制的迭代学习控制方案[C]//第29届中国控制会议论文集. 北京: 中国自动化学会, 2010: 5863-5870. |
| [12] | Shi J, Gao F, Wu T J. Robust design of integrated feedback and iterative learning control of a batch process based on a 2D Roesser system[J]. Journal of Process Control, 2005, 15(8): 907-924. |
| [12] | Shi J, Gao F, Wu T J. Robust design of integrated feedback and iterative learning control of a batch process based on a 2D Roesser system[J]. Journal of Process Control, 2005, 15(8): 907-924. |
| [14] | Shi J, Gao F, Wu T J. Robust iterative learning control design for batch processes with uncertain perturbations and initialization[J]. AIChE Journal, 2006, 52(6): 2171-2187. |
| [15] | Kothare M V, Balakrishnan V, Morari M. Robust constrained model predictive control using linear matrix inequalities[J]. Automatica, 1996, 32(10): 1361-1379. |
| [15] | Kothare M V, Balakrishnan V, Morari M. Robust constrained model predictive control using linear matrix inequalities[J]. Automatica, 1996, 32(10): 1361-1379. |
| [17] | Liu T, Gao F. Robust two-dimensional iterative learning control for batch processes with state delay and time-varying uncertainties[J]. Chemical Engineering Science, 2010, 65(23): 6134-6144. |
| [18] | Wang L, Mo S, Qu H, et al. Design of 2D controller for batch processes with uncertainties and interval time-varying delays[J]. Chemical Engineering Science, 2010, 65(23): 6134-6144. |
| [19] | Wang L, Chen X, Gao F. An LMI method to robust iterative learning fault-tolerant guaranteed cost control for batch processes[J]. Chinese Journal of Chemical Engineering, 2013, 21(4): 401-411. |
| [20] | Liu T, Wang Y. A synthetic approach for robust constrained iterative learning control of piecewise affine batch processes[J]. Automatica, 2012, 48(11): 2762-2775. |
| [20] | Liu T, Wang Y. A synthetic approach for robust constrained iterative learning control of piecewise affine batch processes[J]. Automatica, 2012, 48(11): 2762-2775. |

