1 引言
PDF策略是由美国康奈尔大学的Phelan教授基于One-Mater原则率先提出的一种实用性很强的工程控制理论[1],PDF策略的提出主要是为了避免传统PID控制所存在的“积分饱和”和“微分突变”这两个问题. PDF策略根据“One-Master原则”将积分环节作为主控环节,同时,为了保证系统稳定,将微分反馈直接反馈到功率级控制元件的输入处. 大量的研究表明,PDF策略相比PID控制策略具有更强的鲁棒特性、 较强的抗负载扰动能力和好的控制性能,因此,在一些高要求的场合得以研究和应用[2, 3, 4, 5, 6, 7, 8, 9, 10].
文[2]的研究表明,PDF策略应用于变载荷电机控制系统中体现了PDF控制器本身良好的抗负载扰动能力. 但是在实际的工程应用中,存在负载变化很大、 非线性特性严重的问题,同时又需要进行高精度的控制,所以仍然需要对其进行改进以达到所要求的控制目标和精度. 如何提高对这类应用的控制手段,达到所要求的控制目标和精度要求,一直是一个研究热点. 有研究表明,通过负载观测器将系统负载转矩状态变量引入到控制系统中能够提高控制系统的抗负载扰动能力[11, 12, 13, 14, 15, 16]. 本文基于PDF策略的构架,针对无刷直流电机驱动控制系统,通过引入一个负载转矩观测器,将降阶负载转矩观测器融入到PDF控制系统中,建立一个基于负载扰动观测和控制的电机PDF控制系统模型,以期实现对对其抗负载扰动能力的改善和提高. 2 PDF策略控制器设计
PDF策略的控制结构(2阶)如图 1所示,图中,环节1为简化的功率控制元件,R、 Y分别为系统的输入和输出,系统中PDF控制器的设计实际就是图中3个控制参数ki、 kd1、 kd2的设计.
 |
| 图 1 2阶PDF策略控制结构Fig. 1 Control structure of the second-order PDF strategy |
根据文[2]可知,2阶PDF策略控制器的系数设计公式为
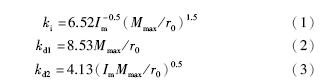
式中,Mmax为末级控制元件的最大输出值,r0为系统阶跃响应输入最大值,Im为被控对象的最大阶项系数. 此系数设计公式是根据特征根结构理论[10]得到的,此公式的特征根配置原则是按照无超调时的最快响应来配置的,根据此公式设计出的PDF控制器具有基本无超调且响应快的特点[2, 17].
本文控制对象为无刷直流电机,该电机基本参数如表 1所示.
| 参数名 | 参数值 |
| 电枢电阻Ra | 0.524 |
| 电枢电感La /mH | 0.390 |
| 转动惯量J /(g·cm2) | 10.5 |
| 转矩常数Km /(N·m/A) | 0.016 9 |
| 最大转速ωmax /(r/min) | 10 400 |
针对该电机所建立的调速系统,其系统末级控制元件的最大输出Mmax即为该电机的最大输出电压24 V,此控制系统做速度调控,因此其阶跃响应输入最大值r0即为电机最大转速10 400 r/min,根据电机的基本参数,简化出电机的数学模型,该数学模型中最高阶项的系数即为Im=5.199×10-7. 将以上数据代入到系数计算公式(1)~(3)得到PDF控制器控制系数为 ki=1.002 4,kd1=0.019 7,kd2=1.430 5×10-4 3 降阶负载转矩观测器设计
负载观测器的设计跟控制对象相关,针对不同的控制对象,根据对象工作原理得到其相应的平衡方程,选取适当的状态变量建立其状态方程. 对于电机,各类电机的平衡方程大体一致,因此本文选取无刷直流电机为控制对象进行观测器设计,以其它种类电机为对象的观测器设计只需针对相应电机工作原理对其平衡方程进行相应修改即可. 3.1 无刷直流电机数学模型
根据无刷直流电机工作原理,得到其数学模型方程如下:
无刷直流电机电磁转矩方程:

式中,Te为电机电磁转矩,Km为转矩常数,φm为每极磁通,Id为电枢电流.
无刷直流电机转矩平衡方程:

式中,TL为包含电机空载转矩的负载转矩,J为转动惯量,ω为转子角速度.
3.2 降阶负载转矩观测器表达式确定
由于电机机械转速信号实际是通过对角度信号进行微分得到的,为了避免引入微分放大的传感器噪声,本文采用伺服控制系统能够直接测量的转角作为已知观测状态变量,这样就避免了采用转速作为已知观测状态变量所引入的微分突变问题. 本文的控制系统为无刷直流电机调速系统,为2阶系统,但在得到电机转角值时已经引入了第3阶,因此若设计一个全阶负载状态观测器则需要设计一个3阶的系统. 鉴于测量结果并不存在严重的噪声干扰且转角信号可以直接测量得到,本文考虑对观测器进行降阶处理,设计降阶负载转矩观测器.
在本文的降阶观测器设计中,本文选取电机的负载转矩和角速度为被观测状态变量,由式(5)可以得到如下状态方程:

将状态方程(6)的状态变量分为可观测的直接测量状态变量和需估测的状态变量,分别定义为xa=θm,xb=[ω TL]T,定义系统输出状态变量y=xa=θm,对式(6)的状态方程进行分块儿,得到新的系统状态方程如下:
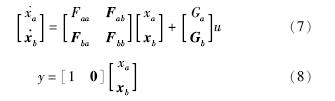
式(7)和式(8)构成了系统分块后的状态方程,式中各参数与式(6)对应,即:

所得到的降阶观测器的结构如图 2所示,图中u为控制量Te,L=[l1 l2]T为观测器的反馈增益,带有“^”符号的参数表示的是相应参数的估计值(观测值).
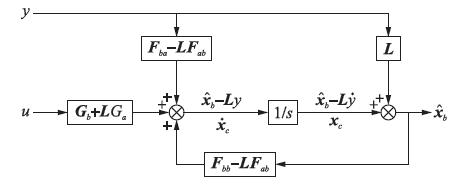 |
| 图 2 降阶观测器结构Fig. 2 Structure of the reduced-order observer |
参考文[14]和文[18]的降阶观测器设计方法,结合图 2所示的降阶观测器结构,可将降阶负载观测器表示为
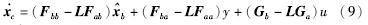
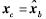 -Ly,它是为了避免进行微分运算造成噪声放大而定义的新状态. 由式(4)和式(9)可以得到如下状态表达式:
-Ly,它是为了避免进行微分运算造成噪声放大而定义的新状态. 由式(4)和式(9)可以得到如下状态表达式:
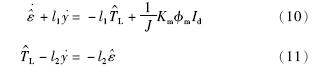
将式(9)和式(11)进一步化简,并进行S变换后可以得到降阶负载观测器的传递函数表达式:

选取合适的反馈增益L是为了获得满意的误差特性[18]. 由式(7)和式(8)化简可以得到不可测量状态变量的状态方程为
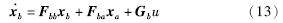
用状态方程(式(13))与状态估计方程(式(9))相减,得到误差的动态方程:
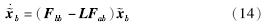
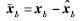 为观测器误差,上式的特征方程为
为观测器误差,上式的特征方程为
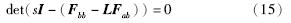
化简式(15)得:

假设期望的观测器误差极点位置为β1、 β2,则期望的观测器特征方程为
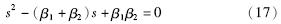
由式(16)和式(17)可得到:
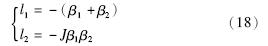
根据本文选取的直流电机的参数,得到系统控制对象的传递函数为
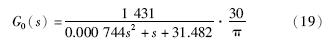
加入PDF策略后的系统传递函数为
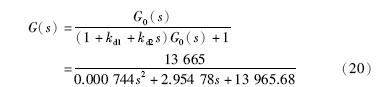
由式(20)可得到控制系统的极点α=-1 985±3 850j.
为了保证观测器误差与期望动态相比衰减得更快,从而使得控制器极点控制整个响应过程,作为一个经验法则,可以将观测器理想极点选得比控制器极点快2~6倍[8]. 同时,在选取观测器理想极点时还应考虑到观测器响应速度过快会导致观测器的带宽过高,从而导致更多的传感器噪声传递到控制执行机构. 综上考虑,本文选取观测器理想极点为控制系统极点的2.5倍,由此得到的观测器理想极点的实部为 β1=β2=-4 962
代入式(18)得到反馈增益L的值,进而将L和其它参数代入式(12)中可以得到降阶负载观测器的各项系数. 4 PDF控制器与观测器融合
为了提高电机PDF策略控制系统的抗负载干扰能力,本文将设计的负载转矩观测器观测的负载转矩值前馈到控制器输出端,组成了一个新的系统,其结构如图 3所示. 本文分别设计了电机的PDF策略控制器和降阶负载转矩观测器. 之所以能将它们融合成一个复合系统是因为此复合系统的主导极点是由控制极点和观测器极点组成的,这说明控制规律和观测器的设计可以独立进行.
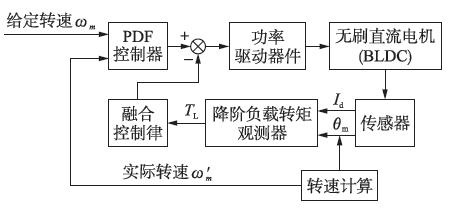 |
| 图 3 控制系统结构Fig. 3 Structure of the control system |
为了实现融合,需要找到观测的负载状态变量与控制器控制量相结合的控制规律. 本文中的PDF策略控制器的输出量为电枢电压,要将二者融合就需要找到观测负载状态变量与电枢电压直接的关系. 无刷直流电机的电压平衡方程式如下:
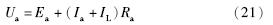
由式(21)知,将观测到的负载转矩状态变量与IL关联即可得到将控制器与观测器融合的控制规律. 由电机原理理论可以知道电流与负载之间存在线性关系,即:

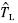 为观测到的负载转矩状态变量,ki为转矩与电流的比例常数.
为观测到的负载转矩状态变量,ki为转矩与电流的比例常数.
通过对系统进行仿真,可以得到几组电机负载电流IL与负载转矩观测量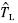 的取值,如表 2所示.
的取值,如表 2所示.
| IL/A | 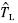 /(N·M) /(N·M)
|
| 0.001 | 0.055 5 |
| 0.002 | 0.111 1 |
| 0.004 | 0.222 2 |
由表 2可得ki=55.5. 结合式(21)和式(22)可知融合控制规律为

对系统进行仿真,验证降阶负载转矩观测器对电机PDF策略控制系统抗负载扰动能力的改善效果. 根据图 3的系统结构图,建立系统的Simulink仿真模型. 在模型中,给定的负载转矩为TL=0.02 N·m,在0.35 s时加入,0.55 s时去掉; 给定的转速为300 r/min.
降阶负载观测器观测到的负载转矩值如图 4所示. 从图中可以看到,观测的负载转矩值与给定的转矩值一致,说明本文设计的降阶负载观测器能够准确地对负载转矩进行观测.
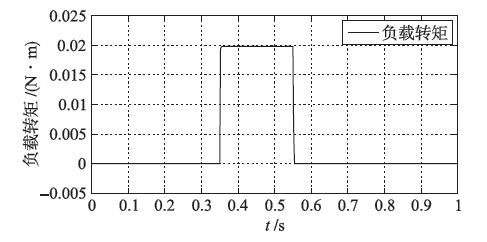 |
| 图 4 负载转矩观测值Fig. 4 Observed values of load torque |
将观测器融入到本文设计的电机PDF控制系统当中,仿真得到的结果如图 5所示. 其中,图右下角的曲线为虚线圈内曲线放大后的图形. 该仿真结果表明: 在未加入降阶负载转矩观测器进行前馈补偿时,在设定的转速和负载转矩条件下,系统的转速波动值达到15 r/min,其调节时间为0.05 s左右; 而进行负载观测前馈补偿后,系统的转速波动最大值约为3 r/min,调整时间减小到了0.007 s左右. 显然,对电机PDF策略控制系统进行负载转矩观测前馈补偿,减小了系统负载突变引起的速度波动和调整时间,提高了电机PDF策略控制系统的抗负载扰动能力.
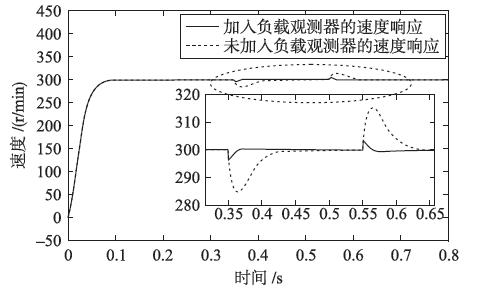 |
| 图 5 抗负载扰动能力对比Fig. 5 Comparison of anti-load disturbance ability |
本文通过将降阶负载转矩观测器所观测的负载转矩状态变量作为前馈引入到电机PDF策略控制系统当中,设计出了抗负载扰动的电机PDF策略控制器. 本文的研究结果表明: 1) 本文采用的将传感器能够直接测量的转角变量作为已知观测状态量的降阶负载转矩设计方法是可行的,设计出的降阶负载转矩观测器能够对转矩进行精确的估计; 2) 本文将观测器观测的转矩作为前馈引入到PDF策略控制系统当中是可行的,不会对系统正常控制造成影响; 3) 本文对电机PDF策略控制系统进行负载转矩观测前馈补偿,降低了负载扰动对系统转速造成的波动,减小了转矩突变时系统速度的调整时间,增强了电机PDF策略控制系统的抗负载扰动能力.
| [1] | Phelan R M. Pseudo-derivative-feedback (PDF) control[D]. California: University of California, 1971. |
| [2] | 李波, 唐猛. PDF策略在变载荷高性能控制系统中的设计与仿真[J]. 工程设计学报, 2013, 20(1): 49-54. Li B, Tang M. Design and performance simulation in integrated platform control system based on PDF algorithm for varied-load object[J]. Chinese Journal of Engineering Design, 2013, 20(1): 49-54. |
| [3] | Tang M, Chen L. The system band width analysis in electro-hydraulic servo system with PDF control[C]//The 5th Asian Control Conference. Piscataway, NJ, USA: IEEE, 2004: 20-23. |
| [4] | Chen L, Xu M H, Ke J. Pseudo derivative feedback control of electro hydraulic speed servos[J]. Journal of Southwest Jiaotong University, 2000, 8(2): 107-113. |
| [5] | Chen L. Robust behavior of subvariable control of pseudo derivative feedback algorithm[C]//The 1989 ASME Design Technical Conferences. 1989: 89-WA/DSC-16. |
| [6] | 曾文火, 周万里, 朱鹏程. 直流电机伪微分反馈位置控制参数优化方法[J]. 电机与控制学报, 2006, 10(6): 562-566. Zeng W H, Zhou W L, Zhu P C. The parameters optimum method of pseudo-derivative feedback algorithm for DC motor position control[J]. Electric Machines and Control, 2006, 10(6): 562-566. |
| [7] | Richard M. Phelan. A simplified approach to feedback control system design[C]//ASME Design Engineering Conferences Anaheim. 1979: 23-67. |
| [8] | Tang M, Xiao S D. The performance improvement in electro-hydraulic servo system with PDF control[C]//The 2nd International Conference on Computer and Automation Engineering. Piscataway, NJ, USA: IEEE, 2010: 26-28. |
| [9] | 丁策, 戴明, 李嘉全, 等. 机载光电陀螺稳定平台的伪微分反馈控制[J]. 光电工程, 2012, 39(10): 128-134. Ding C, Dai M, Li J Q, et al. The PDF control of airborne photoelectric gyro stabilized platform[J]. Opto-Electronic Engineering, 2012, 39(10): 128-134. |
| [10] | 曾文火, 朱鹏程. 电枢控制式直流电机伪微分反馈速度调节系统设计[J]. 电机与控制学报, 2005, 9(2): 171-174. Zeng W H, Zhu P C. The design of speed adjustment of armature control DC motor using pseudo-derivative feedback algorithm[J]. Electric Machines and Control, 2005, 9(2): 171-174. |
| [11] | 张晓光, 孙力, 赵克. 基于负载转矩滑模观测的永磁同步电机滑模控制[J]. 中国电机工程学报, 2012, 32(2): 111-116. Zhang X G, Sun L, Zhao K. Sliding mode control of PMSM based on a novel load torque sliding mode observer[J]. Proceedings of the CSEE, 2012, 32(2): 111-116. |
| [12] | Ko J S. MRAC load torque observer for position control of a brushless DC motor[J]. International Journal of Electronics, 1996, 80(2): 622-627. |
| [13] | Zhang C F, Jia L, He J. Load torque observer based sliding mode control method for permanent magnet synchronous motor[C]//The 25th Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2013: 550-555. |
| [14] | 张兵, 唐猛, 廖海洲. 基于负载观测的PMSM滑模抗扰动自适应控制[J]. 工程设计学报, 2013, 20(5): 427-433. Zhang B, Tang M, Liao H Z. Anti-disturbance adaptive sliding mode control of PMSM based on load torque observer[J]. Chinese Journal of Engineering Design, 2013, 20(5): 427-433. |
| [15] | 解后循, 高翔. 无刷直流电机参数自适应负载观测器设计[J]. 机械科学与技术, 2011, 30(2): 237-241. Xie H X, Gao X. Design of an adaptive load observer for a brushless DC motor[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(2): 237-241. |
| [16] | 陈荣, 邓智泉, 严仰光. 基于负载观测的伺服系统抗扰研究[J]. 中国电机工程学报, 2004, 24(8): 103-108. Chen R, Deng Z Q, Yan Y G. Research on resist-disturbance performance of servo system based on load observer[J]. Proceedings of the CSEE, 2004, 24(8): 103-108. |
| [17] | 卜柏营, 唐猛, 李海. 基于PDF策略的电机调速系统设计与仿真[J]. 重庆理工大学学报, 2011, 25(8): 52-59. Bo B Y, Tang M, Li H. Design and simulation for electromotor speed regulation system based on PDF strategy[J]. Journal of Chongqing University of Science and Technology, 2011, 25(8): 52-59. |
| [18] | Franklin G F, Powell J D, Emami-Naeini A. 动态系统的反馈控制控制[M]. 4版. 北京: 电子工业出版社, 2004: 367-386. Franklin G F, Powell J D, Emami-Naeini A. Feedback control of dynamic systems[M]. 4th ed. Beijing: Publishing House of Electronics Industry, 2004: 367-386. |
| [19] | Dorf R C, Bishop Robert H. 现代控制系统[M]. 11版. 北京: 电子工业出版社, 2011: 636-653. Dorf R C, Bishop Robert H. Modern control systems[M]. 11th ed. Beijing: Publishing House of Electronics Industry, 2011: 636-653. |
| [20] | Chen L. Selection of control coefficients for the optimum linear systems[R]. New York, NJ, USA: ASME, 1984: 84-WA/DSC-15. |



