1 引言
非最小相位行为在工业过程中是普遍存在的,它是指具有右半复平面零、 极点或延时的线性对象[1],如水轮机调速系统、 动力锅炉的主汽压对象、 锅炉汽包水位系统、 飞机高度调节系统等都具有明显的非最小相位特征. 其中,只具有右半复平面零点的系统是一类典型的非最小相位系统. 由于右半复平面零点的存在,系统的阶跃响应存在负调,这对工业控制产生了很大的影响,因此同时抑制超调、 负调和确保调整时间也就成了此类非最小相位系统控制器设计的关键难题[2, 3].
针对非最小相位系统的控制问题,文[4]提出了一种新的拉格朗日基函数迭代学习控制算法,将迭代学习控制转换在有限的输入输出空间中进行. 文[5]提出了分数阶的学习律设计,但并不能保证能够完全补偿非最小相位系统的所有的相位滞后; 文[6, 7, 8, 9]将扰动观测器理论应用于非最小相位的控制,并取得了一些研究成果,但对被控对象的限制条件太多. 文[10]提出使用两个具有积分补偿的固定频率滑模控制器来消除非最小相位特性给系统带来的不良影响. 文[11]通过串加比例—微分(PD)控制方式降低系统阶次,设计尼科尔斯曲线的比例—积分—微分(PID)控制器. 文[12]提出了自适应高增益控制和低幅值反馈控制结合的非线性控制器. 文[13]采用迭代学习方法设计控制器,实现系统输出对期望轨迹的完全跟踪. 文[14]采用饱和非线性控制实现了X-Z倒立摆的稳定控制,如何提高X-Z倒立摆控制的鲁棒性能需要进行进一步的研究. 以上方法都是针对某一特定条件设计的,所能实现的控制效果有限,而且结构复杂,实际应用中组态、 整定困难,大多停留在实验室仿真阶段.
PID控制因其结构简单、 容易实现、 鲁棒性强等特点,仍然是工业过程中应用最广泛的控制算法. 文[15, 16]对目前PID控制器的整定方法进行了详细的总结与比较,其中比较著名的是Ziegler-Nichols经验公式整定方法、 Cohen-Coon整定方法和S-IMC整定方法. Cohen-Coon法是针对1阶滞后模型(FOPDT模型)而提出的一种PID参数整定方法; S-IMC法是一种基于内模控制的PID参数整定方法,不仅适用于1阶模型而且也适用于2阶模型. 这2种方法都有较大的超调量和上升时间,应用在非最小相位系统中也不能有效克服系统负调,所以控制性能不佳; 文[17, 18]与智能算法相结合研究了新的PID整定方法,虽然将PID参数整定问题视为一个多目标优化问题,将系统的超调量、 上升时间和调节时间同时作为待优化的目标函数. 但是,应用在具有右半复平面零点的非最小相位系统PID控制器整定中效果并不理想,3个目标函数并不能及时有效反映出系统负调的克服情况,此外智能整定算法在实际应用中编程复杂,不易于应用. 文[19]给出了一种分数阶内模PID控制器的设计方法,该方法不仅需要采用最小二乘原理对模型进行简化,而且还需要与内模控制原理相结合,使得该方法目前仍处于仿真研究阶段. 文[20]针对高维多变量时滞系统,基于内模控制原理提出分散PI控制器设计新方法. 该方法受到分散结构和PI控制结构的限制,使得强耦合多变量系统的解耦性能不佳,导致系统的性能不能满足相应的控制要求.
本文通过分析具有右半复平面零点的非最小相位系统的动态特性及PID控制特性,将一种大滞后系统的两步PID参数整定方法应用于此类对象的控制,仿真结果表明,该方法完全可以抑制系统的超调和负调且调整时间短、 鲁棒性强,是一种值得推广的工程整定方法.
2 动态特性分析式(1)是具有一个右半复平面零点的非最小相位系统:
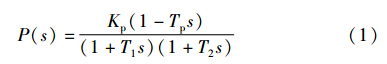
其中,Kp,Tp,T1,T2>0. 将纯迟延环节e-τs采用Pade近似展开得

其中,τ为纯迟环节的滞后时间.
式(1)和式(2)都含有一个右半复平面的零点,如果给式(1)配置一个左半复平面的零、 极点,那么式(1)的非最小相位系统就变成了一个稳定的滞后系统:
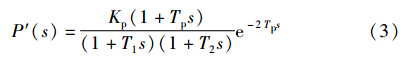
某燃煤锅炉主汽压在汽机调门扰动下的传递函数如式(4)所示:
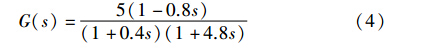
转化为滞后对象为
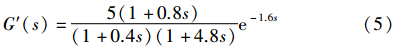
式(4)和式(5)的开环阶跃响应如图 1所示.
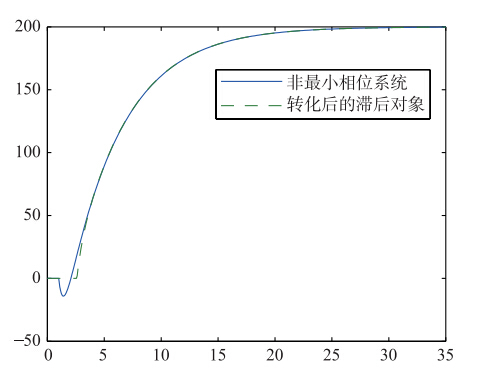 |
| 图 1 对象的开环特性Fig. 1 Open-loop characteristics of the plants |
由图 1开环特性的对比可以看出,在滞后时间(τ=1.6)之后,两个对象的开环特性曲线完全重合,动态特性相同. 在滞后时间之内,非最小相位对象有明显的时滞和负调. 对于非最小相位对象来说,PID参数整定的困难来自于滞后时间之内的一段特性曲线,以比例系数Kc为例,作用过强会引起负调的加剧,甚至于过调,比例作用太弱,调整时间会过长. 尤其从开环特性来看,非最小相位系统不仅有负调还有时滞,因此合理地加入微分作用是非常必要的. 综上所述,如何合理地设计滞后时间之内一段曲线的PID参数,对于非最小相位系统的控制器设计来说至关重要.
从图 1的特性对比也可以看出,含有迟延环节的非最小相位系统是含有右半复平面零点非最小相位系统的一种特殊情况.
3 PID控制特性分析PID控制器的典型系统如图 2所示.
 |
| 图 2 PID控制系统Fig. 2 PID control system |
PID控制器输出u(t)如式(6):
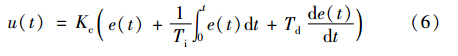
式中,Kc、 e(t)、 Ti、 Td分别为控制器比例增益、 输入偏差信号、 积分时间常数和微分时间常数.
控制器的传递函数为

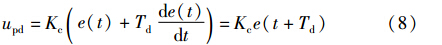
从式(8)可以看出,PD的作用可以看作是对误差在t+Td时刻的线性预测.
式(7)并不是实现PID控制算法的唯一形式,PID控制算法也可是如下形式[15]:
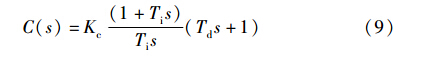
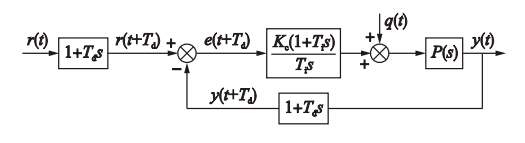 |
| 图 3 等价的PID控制系统Fig. 3 The equivalent PID control system |
采用式(9)的控制器可得图 3[15],从图 3可以看出PI控制器的输入信号(t)为
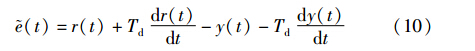
其中r(t)为系统给定值,y(t)为系统输出. 式(10)的误差信号也可以表达为
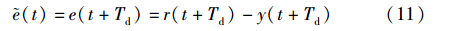
式(10)和式(11)可以清楚地表达出PID控制器对系统误差的超前预测作用.
由以上分析可以看出,只要参数设计合理,PID控制器还是能够克服式(1)所示非最小相位对象的时滞和负调.
式(7)和式(9)中的理想微分作用在实际应用中是无法实现的,式(12)是目前应用广泛的PID控制器形式:
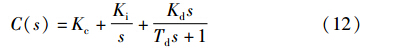
其中,Ki、 Kd分别为控制器积分与微分作用的加权系数.
4 PID参数两步整定方法文[21, 22]针对稳定的时不变2阶大滞后对象式(13)提出了一种有效的PID参数两步整定方法. 第1步,针对稳定的2阶系统G1(s)=kas2+bs+1设计PID控制器参数. 这是容易做到的,现在有多种优化方法来设计这种系统的控制器参数. 第2步,设置和调整控制器前置系数Kf,来达到整定2阶大滞后系统控制器参数的目的:
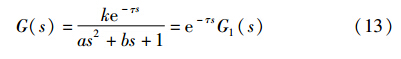
这种方法的主要优点是通过调整前置系数Kf来同时调整PID控制器的4个参数,即Kc、 Ki、 Kd、 Td,达到克服纯滞后时间τ的目的,使得控制器参数整定简单实用. 另外,2阶系统是控制系统中最具代表性的系统. 一般地,对于2阶被控对象所设计的控制器具有通用性[21, 22].
同样,对于式(1)所示的非最小相位对象,首先,利用Pade近似法转化成最小相位带纯滞后的2阶对象,如式(3)所示,然后,便可以借用文[21, 22]的两步整定法进行PID参数整定: 第1步,针对式(3)传递函数的不带纯滞后部分,设计PID参数; 第2步,考虑式(3)中的纯滞后因子,在所得到的PID控制器的前面增设前置系数Kf,调节Kf以克服纯滞后因子对闭环系统性能的不利影响及非最小相位系统的负调.
由于P′(s)毕竟是实际对象P(s)的近似模型,按照上述方法对P′(s)设计出的PID参数,还要进行必要的调整,为此,引进一个比例调整系数α∈(0,1),从而把上述第1步得到的PID表达式(12)修改成式(14):
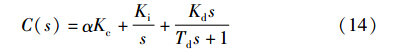
其中,α∈(0,1). 最后,得到整个控制系统结构(如图 4所示).
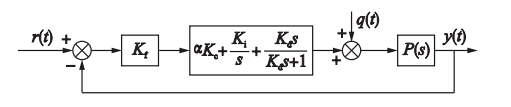 |
| 图 4 系统结构图Fig. 4 The system structure |
由文[21, 22]可得,前置系数Kf是h=Tptp的单调递减函数,tp是系统阶跃响应曲线超调量的第一个峰值时间,Kf=f(h)可以通过曲线拟合的方法得到.
5 实例仿真
采用图 4所示的控制系统,令P(s)=G(s),对式(4)的对象进行仿真实验,并同文[15, 16]中提到的Ziegler-Nichols和S-IMC整定方法进行对比,整定参数见表 1,仿真结果如图 5所示. 由图 5可以看出,两步整定方法没有产生负调和超调,而且也没有牺牲系统调整时间,效果明显好于Ziegler-Nichols和S-IMC的方法.
|
整定方法 | 控制系统参数 |
| 两步整定 | Kf=0.05 α=0.4 Kc=0.5 Ki=0.286Kd=0.1 Td=1 |
| Ziegler-Nichols | Kc=0.06 Ki=0.086 Kd=0.48 Td=1 |
| S-IMC | Kc=0.12 Ki=0.017 Kd=0.48 Td=1 |
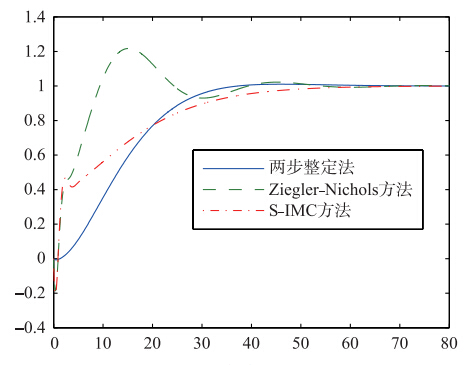 |
| 图 5 仿真结果Fig. 5 The simulation results |
为了考量不同过程模型下闭环系统的鲁棒性,可以认为控制对象P(s)是一系列线性模型的集合,即P(s)=Pn(s)+ΔP(s),其中Pn(s)是过程对象的标称模型. 因此,在控制器参数不变的情况下,将式(4)的控制对象的各个参数均改变±20%进行仿真实验,结果如图 6所示. 由图 6可以看出,系统的最大超调量也没有超过5%.
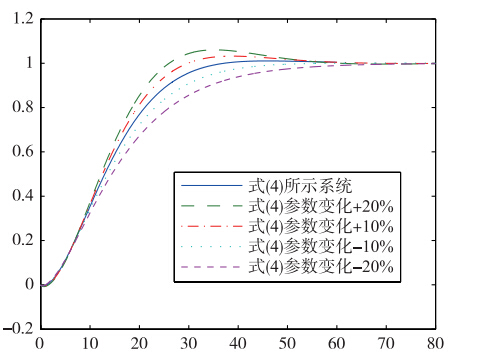 |
| 图 6 不同过程模型的鲁棒性测试1Fig. 6 The robustness test 1 of different models |
进一步考量了不同过程模型下闭环系统的鲁棒性,图 7是控制器参数不变的情况下,将过程模型式(4)的分子、 分母分别增大、 减小20%或者减小、 增大20%的仿真结果. 由此可以看出这一组仿真结果优于将式(4)的各个参数均改变±20%的情形.
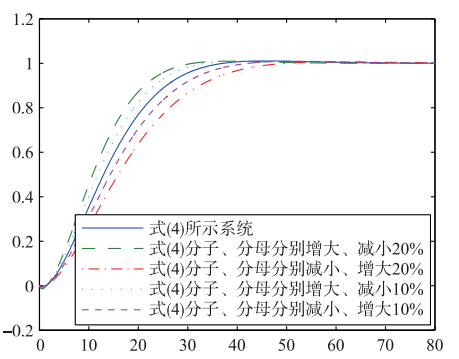 |
| 图 7 不同过程模型的鲁棒性测试2Fig. 7 The robustness test 2 of different models |
工程应用中图 4系统结构图中的扰动q(t)是指控制器输出执行机构的误差,实际应用中以阀门为例,执行机构的抖动误差超过5%就认为非常大了. 因此,在图 4扰动q(t)处分别加入3%和5%的阶跃信号,来考量闭环系统对于扰动的鲁棒性,如图 8所示.
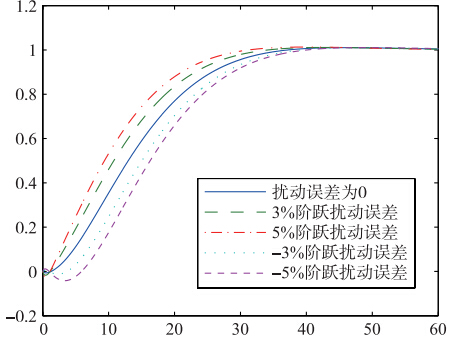 |
| 图 8 扰动鲁棒性测试Fig. 8 The robustness test result under disturbance |
由图 8可以看出,执行机构输出误差为正值,也就是说执行机构的输出比控制器的输出响应更快时,系统调节时间快并伴有少量的超调; 而当执行机构扰动为负值,也就是说执行机构的输出比控制器的实际输出小,执行机构跟不上控制器的调整速度,系统的上升时间变慢,对负调的克服不是非常理想.
6 结论
(1) 具有右半复平面零点的非最小相位对象,其开环动态特性不仅具有一定的时滞还具有很强的负调特性. PID控制不仅能够实现无差调节,而且对于系统误差还具有一定的超前预测作用. 只要合理设置PID控制器参数完全可以达到克服此类非最小相位系统时滞和负调的目的.
(2) 本文将一种2阶大滞后系统的PID参数两步整定方法应用于非最小相位系统的控制,成功克服了由右半复平面零点引起的时滞和负调,控制效果明显好于Ziegler-Nichols和S-IMC整定方法,仿真实验证明了该方法的有效性和鲁棒性. 该方法整定简单、 鲁棒性好,值得在工程应用中推广.
| [1] | 詹习生. 基于通信约束的网络化控制系统最优性能研究[D]. 武汉: 华中科技大学, 2012. Zhan X S. On optimal performance of networked control system with communication constraints[D].Wuhan: Huazhong University of Science and Technology, 2012. . |
| [2] | 王后能. 控制系统的性能优化分析与设计限制研究[D]. 武汉: 华中科技大学, 2009. Wang H N. Performance optimization and design limit research of control system[D]. Wuhan: Huazhong University of Science and Technology, 2009.. |
| [3] | 梁兆阳. 基于神经网络的非最小相位控制系统的研究[D]. 河北: 华北电力大学, 2008. Liang Z Y. Research on the non-minimum phase system control based on neural network[D]. Beijing: North China Electric Power University, 2008. 性能优化分析与设计限制研究[D]. 武汉: 华中科技大学, 2009. Wang H N. Performance optimization and design limit research of control system[D].. |
| [4] | 刘山, 刘杰. 非最小相位系统的扩展Laguerre基函数迭代学习控制[J]. 控制理论与应用, 2012, 29(8): 986-992. Liu S, Liu J. Extended Laguerre basis function based iterative learning control for non-minimum phase systems[J]. Control Theory & Applications, 2012, 29(8): 985-992. 性能优化分析与设计限制研究[D]. 武汉: 华中科技大学, 2009. Wang H N. Performance optimization and design limit research of control system[D].. |
| [5] | Ye Y Q, Tayebi A, Liu X P. All-pass filtering in iterative learning control[J]. Automatica, 2009, 45(1): 257-264. |
| [6] | Shim H, Jo N H, Son Y. A new disturbance observer for nonminimum phase linear systems[C]//Proceedings of the American Control Conference. Piscataway, NJ, USA: IEEE, 2008: 3385-3389. |
| [7] | Shim H, Joo Y. State space analysis of disturbance observer and a robust stability condition[C]//Proceedings of the 46th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2007: 2193-2198. |
| [8] | Son Y, Shim H, Jo N H, et al. Design of disturbance observer for non-minimum phase systems using PID controllers[C]//International Conference on Instrumentation, Control and Information Technology. Piscataway, NJ, USA: IEEE, 2007: 196-201. |
| [9] | 谢巍, 何忠亮. 采用改进型扰动观测器的控制方法[J]. 控制理论与应用, 2010, 27(6): 695-700. Xie W, He Z L. A Control method with improved disturbance observer[J]. Control Theory & Applications, 2010, 27(6): 695-700.. |
| [10] | 陈宗祥, 蒋赢, 潘俊民, 等. 基于滑模控制的Z源逆变器在单相光伏系统中的应用[J]. 中国电机工程学报, 2008, 28(21): 33-39. Chen Z X, Jiang Y, Pan J M, et al. A Z-source inverter for a single-phase PV system based on sliding-mode control[J]. Proceedings of the CSEE, 2008, 28(21): 33-39.. |
| [11] | 孔繁镍, 李啸骢, 吴杰康, 等. 基于尼科尔斯PID设计方法的负荷频率控制[J]. 中国电机工程学报, 2012, 32(22): 79-85. Kong F N, Li X C, Wu J K, et al. Design of Nichols PID controller for load frequency control[J]. Proceedings of the CSEE, 2012, 32(22): 79-85.. |
| [12] | Fiorentini L, Serrani A, Bolender M A, et al. Nonlinear control of non-minimum phase hypersonic vehicle models[C]//Proceedings of the 2009 American Control Conference. Piscataway, NJ, USA: IEEE, 2009. 3160-3165. |
| [13] | 陈冰玉, 孙明轩, 朱胜. 输出重定义下的非线性非最小相位系统迭代学习控制[J]. 控制理论与应用, 2010, 27(7): 948-952. Chen B Y, Sun M X, Zhu S. Output-redefinition-based iterative learning control for nonlinear non-minimum phase systems[J]. Control Theory & Applications, 2010, 27(7): 948-952.. |
| [14] | 王家军, 刘栋良, 王宝军. X-Z倒立摆的一种饱和非线性稳定控制方法的研究[J]. 自动化学报, 2013, 39(1): 92-96. Wang J J, Liu D L, Wang B J. Research on one type of saturated nonlinear stabilization control method of X-Z inverted pendulum[J]. Acta Automatica Sinica, 2013, 39(1): 92-96. . |
| [15] | Normey-Rico J E, Camacho E F. Control of dead-time processes[M]. Berlin, Germany: Springer-Verlag, 2007. |
| [16] | 邱亮. 基于阶跃辨识的PID自整定算法研究及其应用[D]. 上海: 上海交通大学, 2013. Qiu L. Research and application on PID auto-tuning control method based on step identification[D]. Shanghai: Shanghai Jiao Tong Uninversity, 2013.. |
| [17] | 袁桂丽, 薛彦广, 刘吉臻, 等. 基于免疫疫苗的主汽温系统PID优化整定[J]. 动力工程学报, 2013, 33(4): 285-289. Yuan G L, Xue Y G, Liu J Z, et al. PID parameter optimization for main steam temperature control system based on immune vaccine algorithm[J]. Journal of Chinese Society of Power Engineering, 2013, 33(4): 285-289.. |
| [18] | 孟丽, 韩璞, 任燕燕, 等. 基于多目标粒子群算法的PID控制器设计[J]. 计算机仿真, 2013, 30(7): 388-391. Meng L, Han P, Ren Y Y, et al. Design of PID controller based on multi-objective particle swarm optimization algorithm[J]. Computer Simulation, 2013, 30(7): 388-391.. |
| [19] | 赵志诚, 张博, 刘志远, 等. 一种分数阶系统内模PID控制器设计方法[J]. 信息与控制, 2014, 43(2): 129-133. Zhao Z C, Zhang B, Liu Z Y, et al. Design method for IMC-PID controller for fractional order system[J] . Information and Control, 2014, 43(2): 129-133.. |
| [20] | 陈强, 栾小丽, 刘飞. 高维多变量时滞系统多环PI控制的解析设计[J]. 信息与控制, 2014, 43(2): 205-210, 216. Chen Q, Luan X L, Liu F. Analytical design of multiloop PI control for high-dimensional multivariable systems with time-delay[J]. Information and Control, 2014, 43(2): 205-210, 216.. |
| [21] | 开平安, 刘建民, 焦嵩鸣, 等. 火电厂热工过程先进控制技术[M]. 北京: 中国电力出版社, 2010. Kai P A, Liu J M, Jiao S M, et al. Advanced control technologies in power plant[M].. Beijing: China Electric Power Press, 2010. |
| [22] | 刘建民. 火电厂热工过程优化控制策略及应用研究[D]. 北京: 华北电力大学, 2009. Liu J M. Optimization control strategies and application studies in thermal system of power plant[D]. Beijing: North China Electric Power University, 2009. . |



