1 引言
从滤波估计技术[1, 2],到多机器人协作[3, 4, 5],再到课堂教学[6, 7, 8],专业的移动机器人生产厂家系列化、 标准化的两差动轮移动机器人为科研和教学工作带来了方便. 针对此类机器人的应用实践显示,一款性能卓越的目标跟踪控制器可以有效促进教研工作.
目标跟踪控制器,这里特指用来连接实验算法和移动机器人两侧轮子硬件接口的代码层. 这一层可用的传感器只有编码器,生产厂商通常开放速度接口,目标跟踪控制器接收上层算法产生的目标点信息,利用航迹推算法确定机器人当前位姿,解算控制量并传送至硬件接口,引导移动机器人从初始位置运动到目标点.
导航和定位是移动机器人技术主要研究方向之一[9] ,目标跟踪控制器最直接的应用是连续跟踪一系列坐标,引导机器人完成预定轨迹. 这些坐标可以由导航算法产生,也可以预先设计好以验证定位算法的精确程度. 在多机器人协作研究中,目标跟踪控制器用于将1阶微分模型转化为Unicycle模型,同时克服实验平台整体时延对算法的干扰[10]. 使用目标跟踪控制器连接算法和硬件接口的另一个显著优势在于,实验过程的任意时刻均可以暂停算法排查问题,此时机器人停止于最后一个目标点.
在此类应用中,对目标跟踪控制器的性能需求是运动的平滑性和有限时间可达性. 由于只有当前位姿和目标坐标,较优的策略是从初始位置到目标点由快及慢运动,并逐渐调整朝向指向目标,体现运动的平滑性. 在接近目标后,保持最低速运动,降低停止时的滑动.
实现上述策略的前提之一是控制信号在驱动器的可执行范围内. 驱动器执行能力有限体现在2个方面: 1) 具有最高速限制. 关于这种情况,文[11, 12]给出了系统的解决方案. 2) 具有最低速限制. 当控制器给出的电机转速低于最低转速后,将导致转速不准确、 抖动和突然的倒转. 商业化的移动机器人为降低成本,采用低分辨率的编码器配合高倍减速器,导致低速性能不佳. 矛盾的是,机器人的正常运动通常需要执行器工作在低于最低转速的情况下. 如果这种情况发生在接近目标区域,机器人会突然偏离目标,为了准确到达,控制器必须重新对位姿加以修正. 不但破坏了运动平滑性要求,而且延长了到达目标位置的时间.
本文的解决思路是提高运动的复杂性: 在机器人距离目标位置较远时,执行文[13]的控制策略; 接近目标后,若机器人朝向仍然偏离目标,则优先调整之,然后缩短与目标点的距离,以避免出现控制量过小的问题. 复杂的运动并不能够使用复杂的算法. 目标跟踪控制器需要运行于机器人内部硬件上且能达到实时控制的要求. 文[13]是一种快速而有效的算法,缺点之一是渐近稳定的. 在距离目标足够近时必然导致控制量过小而超出驱动器的执行范围. 本文的策略是在接近目标位置后使用一种改进的控制算法,与文[13]相比仅有略微不同,因而没有增加额外的运算负荷. 在配置控制器参数时,将移动机器人的结构参数和驱动器转速上下界考虑其中. 驱动器转速上下界由厂商提供,精确的结构参数值可以参考文[14, 15, 16]介绍的实验方法. 这些实验是进行航迹推算前必须的准备工作. 通过直接调用文[14, 15, 16]的实验结果,可以在结构参数矫正完毕的同时得到合适的控制器参数,不再需要为每一台机器人重新编写控制算法,提高了代码的可移植性. 在多机器人协作实验时,可以避免大量重复性工作.
目标跟踪控制器满足运动平滑性和有限时间可达性要求由仿真实验Ⅰ说明,在恶劣条件下的工作可靠性由仿真实验Ⅱ说明. 实验重现仿真Ⅱ的情形,其数据取自一台真实的KheperaⅢ机器人[17].
2 研究问题和建模本文研究的问题可以描述为: 在假设机器人当前位姿(x,y,θ)和目标点(x*,y*)均精确已知的情况下,设计一种可以连接实验算法和移动机器人两侧轮子硬件接口的控制算法. 该算法要求复杂度低,而且在机器人驱动器执行能力有限,特别是具有最低转速限制的条件下,仍能够引导机器人平稳且准确地到达目标位置,同时给出控制器参数的整定方案.
为方便描述,坐标系及相关的符号如图 1所示. 在运动平面上建立世界坐标系{O}. 机器人上附着坐标系{Robot},其原点在两轴中心,x轴正方向指向两轴距中心和前部支撑点的连线方向,y轴正方向指向左轮. 机器人绝对速度正方向为x{Robot},大小用v表示,其转角定义为将x{o}正方向依顺时针转到x{Robot}正方向所经过的角度θ,相应的角速度用ω表示. 为目标角,表示从机器人所在坐标到目标的射线按逆时针旋转到x{Robot}方向所转过的角度. 设rR、 rL为机器人左右轮半径,则机器人的速度(v、 ω)与两轮转速(ωR、 ωL)的关系为[14]
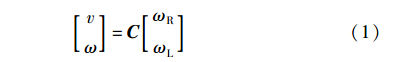
其中,C为两差动轮机器人的结构参数矩阵:
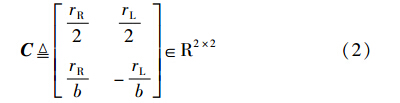
移动机器人两侧轮子驱动器作为物理器件,具有最高和最低速限制,表示为ωR/L<ωmax和ωR/L>ωmin. 文中所有涉及的角度均在[-π,π)之间.
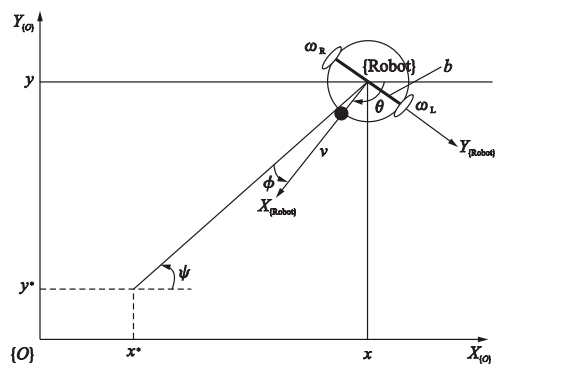 |
| 图 1 机器人运动坐标系定义及各符号表示Fig. 1 Robot motion coordinate system and the representation of the variables |
3 运动控制器设计
移动机器人的当前位姿和目标精确已知,这一假设相对理想. 但是目标跟踪控制器所处的位置仅能够访问到编码器,不足以依靠其规避观测噪声. 机器人到目标点的距离和目标角具有如下关系:r=(x*-x)2+(y*-y)2 =π+θ-ψ其中,ψ=arctany*-yx*-x
目标跟踪控制器在机器人距离目标较远时使用文[13]的控制策略,而接近目标后使用在其基础上略微改进的控制算法. 首先对这种控制器加以分析,然后给出接近目标的判断标准及控制器参数的求解步骤. 文[13]的控制策略如式(3)、 (4)所示,仅有K1、 K2两个待定参数,可以轻易编写为程序并被多数移动机器人的处理器快速执行:

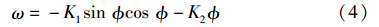
将上述控制策略应用于两差动轮机器人上,及将式(3)、 (4)代入式(1)后得式(5):
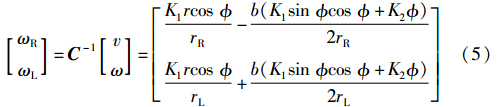
这一变化不会改变文[13]的稳定条件. 可以证明,采用能量函数(6):

得到K1>0且K2>0时,V·<0,这与文[13]的结论一致. 理论上,只要控制参数K1、 K2为正数,则控制律(5)能将两差动轮机器人引导至目标点. 目标跟踪控制只能够获得当前机器人的位姿和目标,这种情况下较优的策略是从初始位置到目标点由快及慢运动,式(5)是一个渐近稳定的控制器,满足要求. 不足之处在于控制量ωR和ωL的大小与目标点距离r相关,实际应用中无论如何设置控制参数K1、 K2,均会导致足够接近目标后ωR/L<ωmin,超出驱动器执行能力范围. 本文使用2个策略应对这一问题: 合理配置控制器参数及在接近目标后微调控制算法. 为说明这一点,定义:
D K1rcos
E b2(K1sin cos +K2 )
式(5)可以简写为

由式(7)可得如下结论: 在某一特定距离r下,目标跟踪控制器能够输出的基础控制量为DrR和DrL,分别对应右轮和左轮. ErR、 ErL是 ≠0时导致在这一基础控制量上的叠加值,并且左右两轮叠加值为异号. 设存在一个临界距离d2,超过这一距离后设法使得DrR和DrL不再随着r变化,并且minDrR,DrL=ωmin,由于叠加值的存在( ≠0),有一侧轮子可以正常工作,而另一侧可能出现控制量ωR/L<ωmin的情况. 启用死区非线性规则,如果这一情况出现,控制量过小的这一侧轮子停转,机器人就会围绕这只不转的轮子为轴旋转,继续调整朝向以指向目标点. 当然,从工程意义的角度,需要在minDrR,DrL略大于ωmin的情况下就启用这一机制. 在机器人到达临界距离d2以后,由于这一机制的存在,机器人的朝向会逐渐指向目标点,直到 接近为0,ωR/L>ωmin条件满足,死区非线性规则不再起作用,两侧轮子将以接近最小转速运动,最终使机器人到达目标点.
这种控制策略的缺陷是,上层算法给出新的目标点以后,控制量会突然增大,这可能导致机械冲击和侧滑. 好在这些实验用移动机器人较文[18, 19]的质量都较小,并且不必运行在复杂的路面条件下,连续发生侧滑的可能性不大. 生产厂商的产品一般都带有软启动功能,可以进一步避免侧滑. 整个实验过程中,最大控制量取决于最大的r. 一个新的算法在试验验证初期通常关注其有效性,研究者不能够保证算法会给出距离多远的目标. 参考实验场地设置合理的K1,进而抑制试验中出现的最高转速. 定义辅助函数:
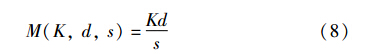
设开始运动时r=d1,s=rmin=min(rR,rL),K=K1,则:
M(K1,d1,rmin)=K1d1rmin
可以用来衡量实验中机器人某侧轮子能够具有的基础控制量,令:
ωmax=M(K1,d1,rmin)
可解出:

例如实验场地大小为M×N(M>N),则可设置d1=N/2比较合适. 待实验算法有效性得到充分验证以后,逐渐增大K1提高实验效率.
接下来考虑r
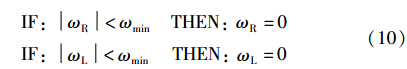
r
可见运算复杂度没有增加:
式(12)与式(5)相比,其实就是让基础控制量与r脱离关系,在以后的运动过程,即使r仍然不断减小,基础速度仍保持不变. 为了充分利用驱动器有效速度范围并避免在到达目标停车时造成侧滑,这一基础速度应为ωmin. 也就是说,在控制律切换以前:
其中rmax=max(rR,rL),可以计算启用条件d2:
启用的控制律应满足:
可得
出于工程应用考虑,略微增大K3以留有裕度. 当 不为0时,ErR、 ErL产生的对基础控制量的叠加不得同时使两侧驱动器均受到式(10)的限制,否则机器人将不能继续运动. 通过调整K2来做到这一点,方法是绘制式(17)关于 的曲线,调整K2使整个曲线均在ωmin的上方:
实践证明,K2的选取范围相对宽裕. 注意过大的K2将导致在 较大的条件下产生很高的角速度,有限的采样速率导致控制量不能及时更新造成超调,机器人蛇形前进影响控制效果.
d1和d2将目标点为圆心的2维空间分为图 2所示的3个部分. d1的取值可由实验场地确定,d由式(14)确定. 在非平稳区内,至少有一侧轮子达到最大转速,转向灵活性受到影响; 在可控区内使用控制策略(5),参数K1由式(9)确定,K2通过绘制(17)的图形获得. 进入接近区后,控制律由(5)变为(12),并启用死区非线性规则(10),K3由式(16)确定. 目标跟踪控制器的程序流程见图 3.

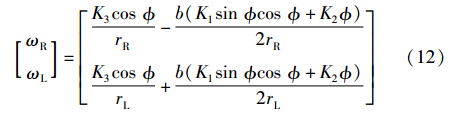
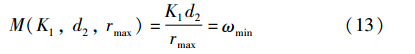

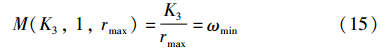

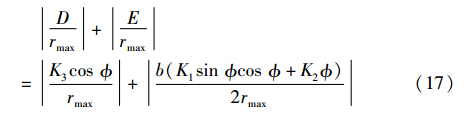
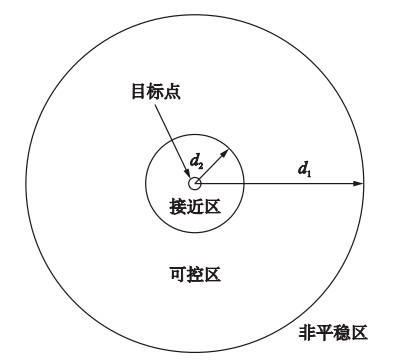 |
| 图 2 目标点周围区域划分Fig. 2 Dividing the surrounding area of the target |
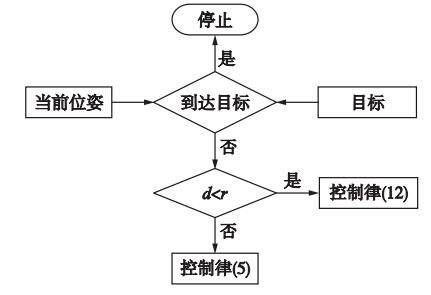 |
| 图 3 目标跟踪控制器程序流程图Fig. 3 The program flow chart of the target tracking controller |
4 仿真和实验验证
为了验证上述控制策略的有效性,进行了大量的仿真和实验,实验参数取自K-Team公司生产的移动机器人KheperaⅢ[17]. 该机器人高70 mm,形状类似直径130 mm的圆形,质量为690 g,标准结构参数: rR=rL=20.5 mm,b=88.41 mm. 驱动两侧轮子的直流电动机内部带有41∶ 1的减速器,加之外部1.6∶1的齿轮箱和软件4倍频,实际轮子转一圈可以得到16×41×1.6×4=4 198.4个脉冲. 驱动器速度范围为: ωmin=0.44 rad/s,ωmax=9.56 rad/s.
厂商向用户开放速度控制接口,两块DsPic单片机分别作为各自轮子的PID速度控制器. 目标跟踪控制器的相关算法运行于内部Intel XSCALE PXA-270@600 MHz嵌入式系统板上,通过I2C总线向PID速度控制器间接传送用户程序的速度指令.
仿真实验展示了具有厂家标准模型参数的KheperaⅢ机器人在4 m×4 m的虚拟环境中运动. 控制器参数为: d1=2 m,K1=0.101 9,d2=0.093 m,基于工程需要,在精确计算的基础上将K3的取值略微放大,取K3=ωminrmax+0.000 1=0.009 6,并取K2=2K1,为与实际验证保持一致,当r<10 mm时认为机器人已经到达目标点.
仿真实验Ⅰ演示了初始位置距离目标较远的情况,目的是说明目标跟踪控制器满足运动平滑性和有限时间可达要求. 仿真实验Ⅱ用以说明即便机器人在接近目标后完全没有转向,目标跟踪控制器仍然能够正常工作. 实验重现仿真Ⅱ的情形,其数据取自一台真实的KheperaⅢ机器人.
4.1 仿真验证
仿真实验Ⅰ中,机器人以初始位姿(2,0,0)运动到目标位置点(0,0),虽然开始时机器人背向目标点(图 5),但由于控制策略(5)的作用,机器人做了一个类似汽车“掉头”动作,逐渐朝向目标. r
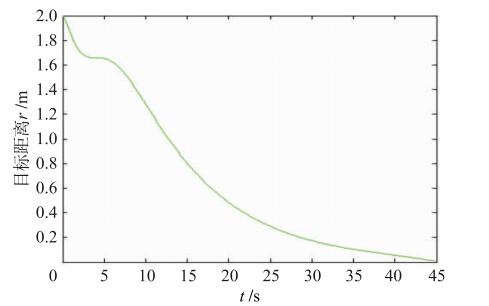 |
| 图 4 仿真Ⅰ:目标距离变化情况图. 随运动的进行,目标距离平滑地逐渐减小Fig. 4 Simulation Ⅰ: Target distance variation. The distance of the target decreases smoothly with the movement |
 |
| 图 5 仿真Ⅰ: 目标角 变化情况图. 目标角 平滑地逐渐减小Fig. 5 Simulation Ⅰ: Target angle variation. The target angle decreases smoothly |
在模拟实验Ⅱ中,将机器人的初始位置调节到“接近区”的外侧,设定为(0.065 8,-0.065 8,-π/4). 可见这是机器人在进入“接近区”以前朝向完全没有得到调整的极端情况. 机器人开始运动时首先调整转向(图 9),大约在(0.06,-0.05)处,一侧轮子被式(10)设置为0,机器人以停转的轮子为轴旋转继续调整朝向,最终指向目标点并满足停止条件,整个运动过程(图 8)控制器没有输出执行
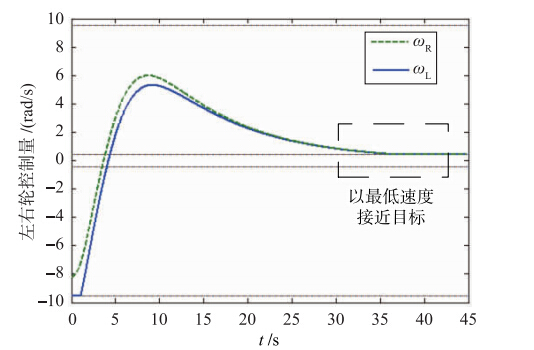 |
| 图 6 仿真Ⅰ:控制量变化情况图.机器人以接近最低速度到达目标.Fig. 6 Simulation Ⅰ: Control signal variation. The robot reaches the goal at a minimum speed |
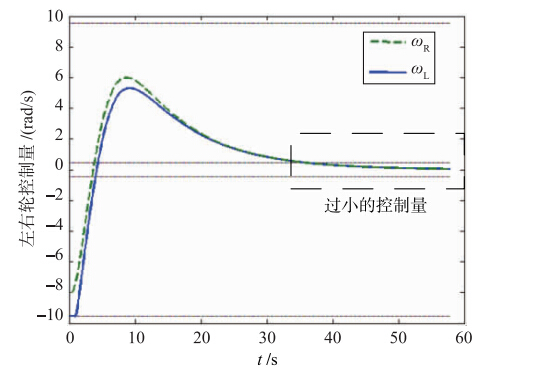 |
| 图 7 控制量变化情况图. 参数与模拟实验Ⅰ完全相同,但仅使用控制策略(5),机器人运动过程中约有1/3的时间控制量均小于ωminFig. 7 Control signal variation. The simulation parameters are the same,but only controller (5) is used. The control commands are smaller than ωmin in about 1/3 of the time |
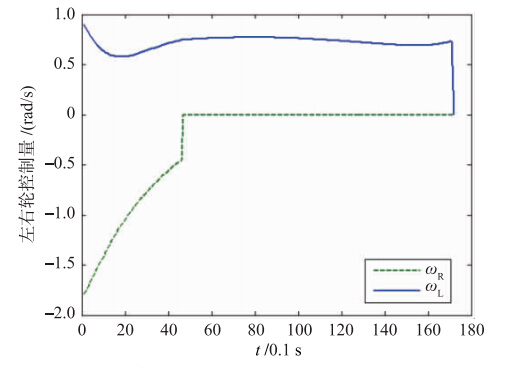 |
| 图 8 仿真Ⅱ: 控制量变化情况图. 大约在仿真开始5 s以后,右侧轮子停止运动Fig. 8 Simulation Ⅱ: Control signal variation. The right wheel stops at 5 s after the simulation began |
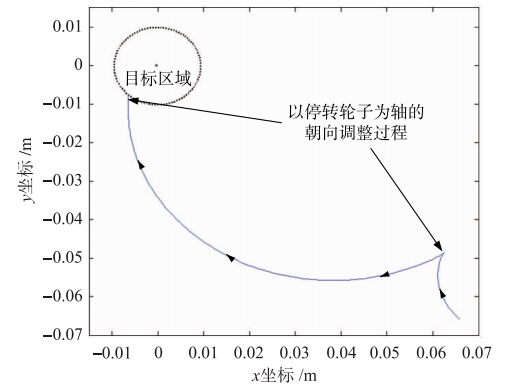 |
| 图 9 仿真Ⅱ:机器人坐标变化图. 仿真开始一段时间,机器人以不转的轮子为轴旋转调整朝向Fig. 9 Simulation Ⅱ: Robot coordinate variation. The robot adjusts its direction by rotating around a stopping wheel for some time since the simulation began |
能力之外的控制量. 这说明在极端情况下,目标跟踪控制器也可以引导机器人到达预期目标并避免了电动机执行能力有限对控制精度的影响.
4.2 实验验证根据模拟实验2,d=0.093 m是一个相对较小的数值. 在实际条件下,捕获并绘制机器人的运动轨线是相对困难的,尽管如此,从实际机器人系统上采集两侧电动机控制指令并加以分析研究,足以判断目标跟踪控制器的有效性. 应用航迹推算以前,需要做类似[14, 15, 16]的结构参数校准实验,本文利用程序包[20]完成之. 校准后的结构参数在机器人初始化过程中部被调用并计算控制器参数K1、 K2、 K3及d2. 每一台参与实验的机器人在完成结构参数校准的同时得到了合适的目标跟踪控制器,这种可移植性在多机器人协作实验时可以避免大量重复性工作. 机器人初始位姿及目标点与模拟实验Ⅱ完全相同. 图 10即为从真实机器人系统上采集的两侧电动机控制指令序列,可以看出与图 8在形状上非常相似,说明控制策略在真实机器人系统上也起到了类似的作用.
5 结论
本文为实验用两差动轮机器人设计了一种目标跟踪控制器并给出了控制器参数的确定方法. 该控制器可以将两差动轮移动机器人引导至目标点而不会受到执行器最低转速限制的影响,应用于低速性能不佳的商业化实验用两差动轮机器人上颇为有效.
利用目标跟踪控制器连接实验算法和移动机器人两侧轮子硬件接口这一技术手段具有广泛的应用. 本文提供的目标跟踪控制器设计方案,在移动机器人距离目标较远时使用控制策略(5),该策略在缩短机器人与目标点之间距离的同时调整机器人朝向使之指向目标. 接近目标后,控制律切换为(12),并启用死区非线性规则(10),此时则优先调整机器人朝向,然后缩短与目标点的距离.
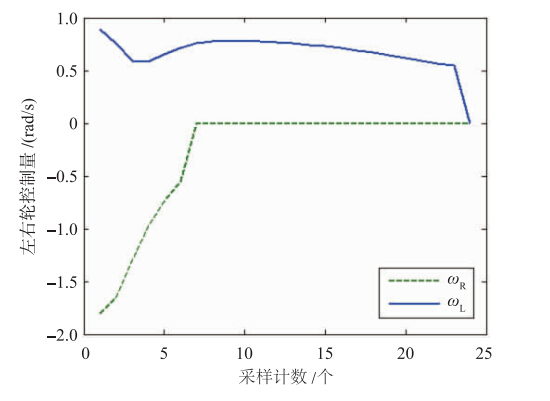 |
| 图 10 基于KheperaⅢ机器人的实验. 约7个采样点以后,右侧轮子停止转动Fig. 10 Experiment on a KheperaⅢ robot. The right wheel stops moving after about 7 sample points. |
引导机器人沿着一条平滑的轨迹,由快及慢地运动到目标点,最终以接近最低速度的方式到达目标,降低停止时发生侧滑的可能性. 涉及的算法非常简单,可以简便地编写为程序代码并快速运行于移动机器人内部处理器上且达到实时控制的要求.
本文给出的控制器参数整定过程,可以与结构参数校准实验同时进行,这一特性在多机器人协作实验中节省大量工作时间.
机器人长期运行的过程中,航迹推算得到的当前位姿必须不断被某种精度更高的定位算法修正. 这些定位算法工作频率通常与依赖的传感器工作频率相同,并且具有更高的运算复杂度,因而不与目标跟踪控制器同步运行. 这些定位算法带给系统的随机扰动随定位原理的不同而不同. 对这些干扰的规避需要多层算法联合设计,不在本文的讨论范围内.
重新关注式(14),在假设rR=rL=r的条件下d2=ωminr/K1. d2决定了控制算法的切换距离,如果d2可以小于定位算法所带来的误差,那么本文讨论的问题就可以被忽略. 但是这要求更小的ωmin,及需要提升驱动器的性能; 更小的轮子半径r,意味着机器人制造的精巧性; 更大的K1,意味着机器人将忍受更强的加减速冲击并面临更高的侧滑风险. 在实验用机器人商业化生产的今天,这些都是需要厂商和用户权衡考虑的问题.
运行在专门设计的平面上,移动机器人轮子频繁打滑的可能性低. 商业化的移动机器人通常只开放速度和步长两种硬件接口,动力学模型、 滑动参数等关键信息缺乏,导致现有优秀研究成果[18, 19]难于应用. 机器人启动时轮子突然转动导致的侧滑通过厂商预设的软起动功能加以规避.
基于KheperaⅢ机器人的模拟和实验显示,本文设计的目标跟踪控制器及提供的控制器参数确定方法,能够引导实验用两差动轮移动机器人在有限时间内沿平滑轨迹运动到目标点,并避免执行器最低转速限制对运动过程的影响.
| [1] | Wang X B, Fu M Y, Zhang H S, et al. Target tracking in wireless sensor networks based on the combination of KF and MLE using distance measurements[J]. IEEE Transactions on Mobile Computing, 2012, 11(4): 567-576. |
| [2] | 安雷, 张国良, 张维平, 等. 移动机器人扩展卡尔曼滤波定位与传感器误差建模[J]. 信息与控制, 2012, 41(4): 406-412. An L, Zhang G L, Zhang W P, et al. EKF localization and sensor error modeling for mobile robots[J]. Information and Control, 2012, 41(4): 406-412. . |
| [3] | Sungwon M, Dongjun K, Kim H J, et al. Cooperative control of differential wheeled mobile robots for box pushing problem[C]//International Conference on Control, Automation and Systems. Piscataway, NJ, USA: IEEE, 2012: 140-144. |
| [4] | 王牛, 李祖枢, 潘娅, 等. 基于意图的多智能体协调机制及其在Mirosot机器人足球系统中的应用[J]. 机器人, 2007, 29(6): 590-595. Wang N, Li Z S, Pan Y, et al. An intention-based multi-agent coordination mechanism and its application to Mirosot soccer robot systems[J]. Robot, 2007, 29(6): 590-595.. |
| [5] | 程磊. 多移动机器人协调控制系统的研究与实现[D]. 武汉: 华中科技大学, 2005. Cheng L. Research and implementation on multiple mobile robots coordination control system[D]. Wuhan: Huazhong University of Science and Technology, 2005. . |
| [6] | Mondada F, Bonani M, Raemy X, et al. The e-puck, a robot designed for education in engineering[C]//9th Conference on Autonomous Robot Systems and Competitions. 2009: 59-65. |
| [7] | 李成林. 基于e-puck机器人的多智能体实验平台的设计[D]. 哈尔滨: 哈尔滨工业大学, 2013. Li C L. Multi-agent platform design based on e-puck[D]. Harbin: Harbin Institute of Technology, 2013.. |
| [8] | de la Croix J P, Egerstedt M. Flipping the controls classroom around a MOOC[C]//American Control Conference. Piscataway, NJ, USA: IEEE, 2014: 2557-2562. |
| [9] | 李磊, 叶涛, 谭民, 等. 移动机器人技术研究现状与未来[J]. 机器人, 2002, 24(5): 475-480. Li L, Ye T, Tan M, et al. Present state and future development of mobile robot technology research[J]. Robot, 2002, 24(5): 475-480. . |
| [10] | Ren W, Chao H Y, Bourgeous W, et al. Experimental validation of consensus algorithms for multivehicle cooperative control[J]. IEEE Transactions on Control Systems Technology, 2008, 16(4): 745-52. |
| [11] | 马海涛. 非完整轮式移动机器人的运动控制[D]. 合肥: 中国科学技术大学, 2009. Ma H T. The motion control of nonholonomic wheeled mobile robots[D]. Hefei: University of Science and Technology of China, 2009.. |
| [12] | 韩光信. 控制受限的非完整轮式移动机器人运动控制研究[D]. 长春: 吉林大学, 2009. Han G X. Study on motion control for nonholonomic wheeled mobile robots[D]. Changchun: Jilin University, 2009. . |
| [13] | Lee S O, Cho Y J, Hwang-Bo M, et al. A stable target-tracking control for unicycle mobile robots[C]//International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2000: 1822-1827. |
| [14] | Antonelli G, Chiaverini S, Fusco G, et al. A calibration method for odometry of mobile robots based on the least-squares technique: Theory and experimental validation[J]. IEEE Transactions on Robotics, 2005, 21(5): 994-1004. |
| [15] | Kelly A. Fast and easy systematic and stochastic odometry calibration[C]//International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2004: 3188-3194. |
| [16] | Borenstein J, Feng L Q. Measurement and correction of systematic odometry errors in mobile robots[J]. IEEE Transactions on Robotics and Automation, 1996, 12(6): 869-880. |
| [17] | Schmidt L, Buch B, Burger B, et al. KheperaⅢ Mobile Robot-Practical aspects[DB/OL]. [2014-11-24].. |
| [18] | 叶锦华. 不确定非完整轮式移动机器人的运动控制研究[D]. 广州: 华南理工大学, 2013. Ye J H. Research on motion control of uncertain nonholonomic wheeled mobile robot[D]. Guangzhou: South China University of Technology, 2013.. |
| [19] | 崔明月. 复杂环境下不确定轮式移动机器人运动控制的研究[D]. 重庆: 重庆大学, 2012. Cui M Y. Research on motion control in the complex environment for the wheeled mobile robots with uncertainties[D]. Chongqin: Chongqing University, 2012. . |
| [20] | Prorok A, Arfire A, Bahr A, et al. KheperaⅢ toolbox[CP/DK]. [2014-11-24]. . |



