1 引言
数据分类是机器学习和模式识别的基础. 主要方法有支持向量机[1, 2]、 核密度评估[3]; 为进一步提高精度的半监督支持向量机[4],还有用于一类分类的支持向量数据描述(support vector data description,SVDD)[5]和最小球最大间隔方法[6]等. 这些方法都可以用公式表示为二次规划问题. 假如给定n个样例,求解对应的二次规划问题的计算复杂度为O(n2)(甚至为O(n3)),严重限制了这些方法用于训练大规模数据集.
许多学者已经找到了不同的方法来降低求解二次规划问题的复杂度. 典型的方法包括分块算法和复杂的分解算法如SMO(sequential minimal optimization,SMO)算法[7]、 贪婪逼近[8]、 取样方法[9]和矩阵分解[10]. 最近Tsang等人提出的核向量机(core vector machine,CVM)[11, 12]将二次规划问题转化为求解一个最小包围球(MEB)问题,并使用快速近似算法寻找MEB,为求解二次规划问题展开了全新的方向. 最近胡文军等人又提出了最大向量夹角间隔分类算法(MAMC)[13],并且证明了核化的MAMC等价于核化的MEB问题.
本文在文[13]的基础上,提出了求解最优向量d的不同方法,得到中心夹角间隔分类器(CAMC). 进而证明CAMC也等价于核化的MEB,但是应用MEB进行求解时,可以发现MEB的结构严重依赖于调和参数的选择,从而影响了其分类精度. 受文[14]的启发,提出了正则化核向量机(RCVM),进而与CAMC结合得到中心向量夹角间隔正则化核向量机(CAMCVM). 基于大量基准数据集的实验表明,CAMC具有与MAMC相同的分类性能,并且CAMCVM可以有效训练大规模数据集,而且CAMCVM的分类精度高于文[13]中的最大向量夹角间隔核向量机(central vector-angular margin core vector machine,MAMCVM).
2 背景给定样本集{(xi,yi),i=1,2,…,m,m+1,…,n},其中xi∈Rd,yi∈{+1,-1}为对应的类标,yi=+1(1≤i≤m),yi=-1(m+1≤i≤n).
2.1 最小包围球问题
目前,最小包围球问题[15, 16, 17]受到了普遍关注. 最小包围球问题旨在找到一个能包含所有样本点的超球. 这个超球用B(c,R)表示,其中c和R分别表示球的中心和半径. 最小包围球问题表示如下:

引入拉格朗日函数,得对偶问题如下:
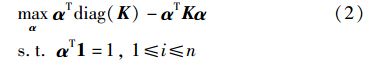
其中,K=[ T(xi) (xj)]n×n是对应的核矩阵. 此问题等价于一类的硬间隔SVDD.
2.2 支持向量数据描述Tax和Duin 2004年提出了支持向量数据集描述算法(SVDD),旨在找到一个超球包含所有的正常点,检测出异常点. 给定关于映射 的核函数k. SVDD的优化问题公式化如下:
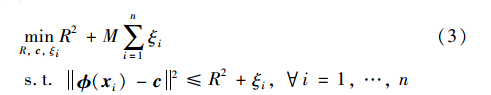
其中,M是调和参数,用于调节边界和误差; c和R分别表示球B(c,R)的中心和半径. 引入拉格朗日函数,得对偶问题如下:
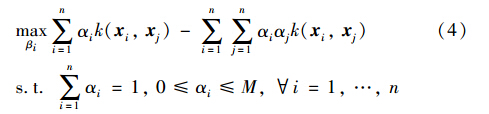
表示成矩阵形式为
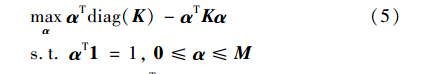
其中,α=[α1,α2,…,αn]T是拉格朗日乘子. M是各项都为M的n维向量.
2.3 最大化向量夹角间隔分类器2012年胡文军等人基于向量夹角距离提出了一种新的分类算法. 即在样例的特征空间找到最优向量d,再根据训练点与d的向量夹角距离对训练点进行分类. 理论上VC维的上界依赖于包围所有训练样例的最小包围球的半径,所以向量d应尽量靠近训练样例的中心,因此上面的问题可公式化为
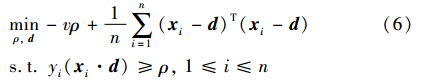
根据欧氏几何,xTid是个实数,并且xTid=xidcosθi,θi是xi与d之间的向量夹角,所以xTid实际反映的是xi与d在欧氏空间中夹角与距离的信息. 因此称之为向量夹角,式(6)中的参数ρ称为向量夹角间隔. 此方法被称为最大化向量夹角间隔分类器. 引入拉格朗日函数,得到对偶问题:

引入核函数k(xi,xj)= T(xi) (xj)后,对偶问题(7)变为
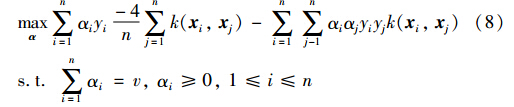
最优向量:

根据上面的公式还可得

其中,S={xiαi>0,1<i<n}.
根据式(9)和式(10),可以得到决策函数:
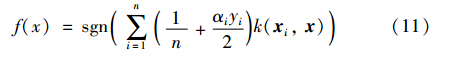
3 中心夹角间隔分类器
考虑到不平衡数据集,为了让d尽量靠近数据集的中心,考虑让d同时靠近正类样例和负类样例的中心. 此方法优化问题如下:
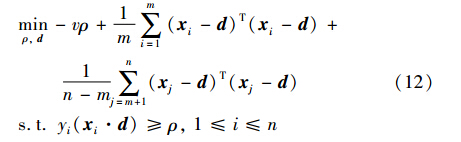
为了得到上面优化问题的对偶形式,引入拉格朗日函数得
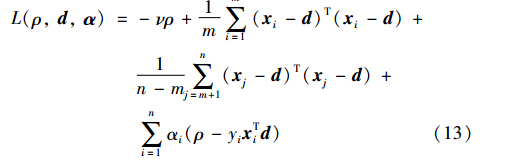
其中,α=[α1,α2,…,αn]T是拉格朗日乘子. 令函数L(ρ,d,α)对ρ、 d求偏导为0得


由式(15)得

把式(14)、 (16)代入式(12),可以得到对偶问题:
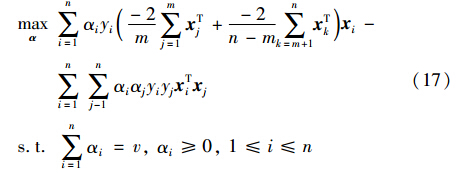
若 为特征映射,则用核函数k(xi,xj)= T(xi) (xj)代替xi·xj,可得如下形式:
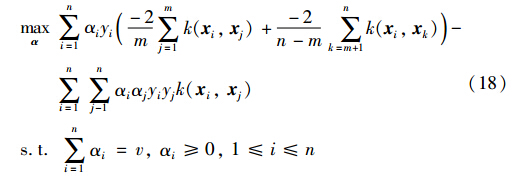
那么ρ和决策函数f(x)如下:

其中,S={xiαi>0,1<i<n}.
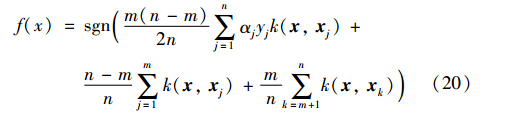
容易看出,上述问题为二次规划问题,所以求解的计算复杂度为O(n3),因此限制了此方法用于训练大规模数据集. 下一部分将证明此方法等价于MEB问题,可以用CVM求解,从而此方法就可以快速训练大规模数据集.
4 中心向量夹角间隔正则化核向量机
4.1 正则化核向量机
应用CVM训练数据集,寻找最小包围球时,可以发现球的结构对所选择的调和参数M非常敏感,尤其是在目标函数中直接应用惩罚项M∑ni=1ξi时,球的体积和分类精度严重依赖于参数M. 因此应该给每个样本点一个不同的调和参数,以此来反映此点被包含在超球中的可能性. 给每个样本点一个权重,用此权重代替参数M,从而提高参数的分类精度.
权重wi是用特征样例xi(i.e. (xi))到特征空间样例中心i.e.1n∑nj=1 (xj)的距离的倒数定义的,即在特征空间中距离中心越远的点所给权重越小. 为了计算正则化权重,首先通过核矩阵K计算一个核向量距离D =[D ll=1,2,…,n].
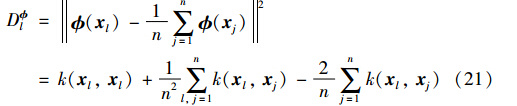
权重wi, i=1,…,n,通过以下公式计算:
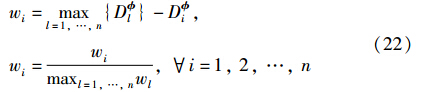
权重wi(i=1,…,n)用于代替调和参数M,则优化问题表示如下:
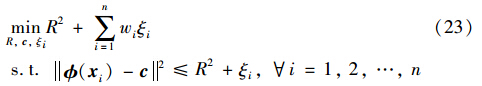
在优化问题(23)中,每一个权重wi反映了对应数据点xi成为异常点的可能性. 通过引入拉格朗日函数,可以得到对偶问题如下:

值得注意的是,拉格朗日乘子βi(i=1,…,n)的上界不再是同一个. 每一个的上界都由权重wi来控制. 显然这是一个二次规划问题,优化参数β,可以得到:
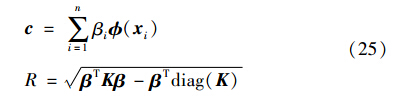
4.2 CAMC与中心限制最小包围球的关系
首先令αi=νβi,并代入对偶问题(18)中,得:
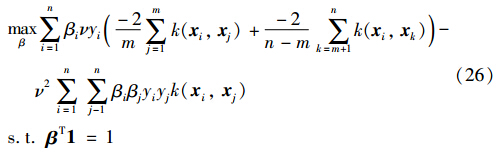
上面的优化问题等价于:
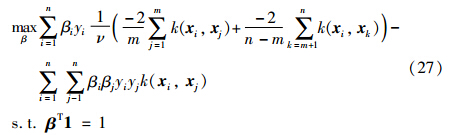
令:
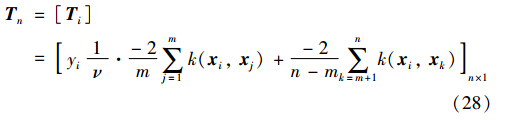
Tn是式(27)中的线性系数向量. 再用αi代替式(27)中βi,式(27)变为
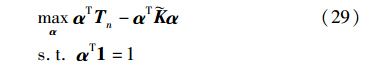
其中,=[yiyjk(xj,xj)]n×n是对应的核矩阵. 通过定义
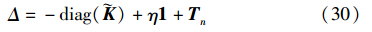
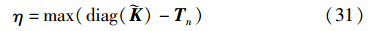
式(29)可以写成如下形式:
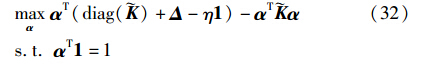
其中,Δ≥0. 因此可以将CAMC看成中心限制最小包围球问题,进而可以将CAMC和RCVM结合得到CAMCVM,进行大规模数据集的训练.
4.3 CAMCVM的算法基于CAMC与中心约束MEB的关系,给出了快速的训练算法CAMCVM,此方法将CAMC与RCVM相结合,可以有效训练大规模数据集. CAMCVM算法包括2个阶段: 第1阶段应用RCVM寻找核心集; 第2阶段应用CAMC算法进行训练. 具体步骤如下:
第1阶段 应用RCVM得到核心集
第1步: 初始化ε、 t=0、 St、 ct、 Rt.
第2步: 更新核心集: 如果所有的训练样例都包含在特征空间球B(ct,(1+ε)Rt)中,那么直接转到第6步.
第3步: 在特征空间中找到距离ct最远的点z,令St+1=St∪{z}.
第4步: 找到新的MEB: 应用式(25)求解ct和Rt.
第5步: 令t=t+1,并且跳转到第2步.
第2阶段 用CAMC进行训练
第6步: 用CAMC算法训练核心集.
第7步: 根据式(20)得到决策函数.
5 实验结果
这一部分进行中心向量夹角间隔分类算法和中心向量夹角间隔正则化核向量机算法的性能评估. 实验结果分为2个部分. 第1部分是用CAMC训练小数据集,第2部分是用CAMCVM训练大规模数据集. 在所有的实验中,核函数都选用高斯函数k(xi,xj)=exp-xi-xj2/h,其中h为高斯核参数. 所有的实验都在3.1 GHz Pentium CoreTM,8GB RAM,Matlab R2009a实验平台进行.
5.1 CAMC的性能
本节主要是CAMC与之前的最大向量夹角间隔分类算法的性能进行比较. 所用到的实验数据都来自UCI数据库. 对于每一个数据集包括总样例个数、 正类样例个数、 负类样例个数和维数. 详见表 1. 性能结果用训练时间、 测试时间和测试精度来说明. 在所有的实验中,核参数h根据以下选择{s2/32,s2/16,s2/8,s2/4,s2/2,s2},s为训练数据的平均2范数. 所有数据的70%用于训练,30%用于测试. 正则化参数ν在{2,5,7,9,10,20,50,70}中选择. 性能比较实验结果见表 2和图 1. 从中可以看出,CAMC的测试时间比MAMC的测试时间短,但是训练精度不比MAMC差,甚至比MAMC训练精度还要高.
| 数据集 | 维数 | 样例个数 | 正类个数 | 负类个数 |
| Arrhythmia | 279 | 452 | 245 | 207 |
| B.cancer | 10 | 699 | 458 | 241 |
| C.bench | 278 | 452 | 249 | 203 |
| Wdbc | 31 | 569 | 212 | 357 |
| Iris | 4 | 150 | 56 | 94 |
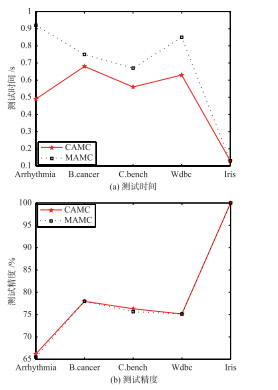 |
| 图 1 CAMC与MAMC的比较Fig. 1 Comparison between CAMC and MAMC |
| 数据集 | 训练时间 /s | 测试时间 /s | 测试精度 /% | |||
| CAMC | MAMC | CAMC | MAMC | CAMC | MAMC | |
| Arrhythmia | 4.36 | 3.96 | 0.49 | 0.92 | 66.20 | 65.49 |
| B.cancer | 53.22 | 52.03 | 0.68 | 0.75 | 77.99 | 77.99 |
| C.bench | 4.54 | 4.48 | 0.56 | 0.67 | 76.31 | 75.66 |
| Wdbc | 34.29 | 36.76 | 0.63 | 0.85 | 75.15 | 75.15 |
| Iris | 0.32 | 0.42 | 0.13 | 0.13 | 100.00 | 100.00 |
将CAMCVM与MAMCVM的性能在大数据集上进行比较,实验数据见表 3,所有的数据都来自UCI数据库. 对于多类标的数据集,将其中一类作为正类,其余的类作为负类进行训练.
| 数据集 | 样本维数 | 样本个数 | 训练样例个数 | 测试样例个数 |
| DNA | 180 | 5 176 | 3 457 | 1 729 |
| Magic | 10 | 19 020 | 9 510 | 9 510 |
| Codrna | 8 | 488 565 | 325 710 | 162 855 |
| Shuttle | 9 | 58 000 | 29 000 | 29 000 |
| Digit | 64 | 5 620 | 2 810 | 2 810 |
| Sat | 37 | 6 435 | 3 217 | 3 218 |
1) 在此实验中,基于Shuttle数据集,获得对于CAMCVM最优的逼近参数ε. 在实验中,随机选取50%作为训练数据,剩下的50%作为测试数据. 实验结果见表 4、 图 2. 从实验结果可以看出,随着逼近参数ε的减小,测试精度逐渐提高,但是训练时间和测试时间逐渐增大. 从图 2中可以看出,当选取ε=1e-4时,可以很好地调和精度和时间. 因此在以下的实验中,选取ε均为1e-4.
| ε | 测试精度 /% | 训练时间 /s | 测试时间 /s |
| 1e-2 | 89.95 | 0.047 | 0.65 |
| 1e-3 | 90.57 | 0.094 | 0.84 |
| 1e-4 | 97.88 | 0.140 | 1.34 |
| 1e-5 | 98.23 | 0.312 | 1.97 |
| 1e-6 | 99.02 | 0.452 | 2.56 |
2) 不同方法的性能比较: 在本实验中,将CAMCVM与MAMCVM的性能进行比较. 核参数和正则化参数分别按以下选取{s2/8,s2/4,s2/2,s2,2s2,4s2},{2,5,7,9,10,20,50,70}. 实验结果见表 5,为了便于观察,还绘制了图 3. 从表 5和图 3中可以看出,在训练时间和测试时间几乎相当的情况下,对于Magic数据集,CAMCVM的训练精度要比MAMCVM高很多; 对于其它数据集,CAMCVM的精度也要高于MAMCVM.
 |
| 图 2 参数ε对CAMCVM的影响Fig. 2 Performance influence of the parameter ε for CAMCVM |
 |
| 图 3 CAMCVM与MAMCVM测试精度实验结果Fig. 3 The comparison results of testing accuracy between CAMCVM and MAMCVM |
| 数据集 | 训练时间 /s | 测试时间 /s | 测试精度 /% | |||
| CAMCVM | MAMCVM | CAMCVM | MAMCVM | CAMCVM | MAMCVM | |
| DNA | 73.46 | 76.60 | 3.23 | 2.90 | 76.63 | 76.63 |
| Magic | 18.41 | 22.41 | 3.33 | 3.12 | 77.19 | 60.26 |
| Codrna | 29.89 | 37.40 | 56.13 | 64.60 | 67.41 | 67.11 |
| Shuttle | 0.23 | 0.31 | 1.42 | 1.86 | 97.88 | 93.71 |
| Digit | 902.65 | 1 123.3 | 6.55 | 6.94 | 99.79 | 98.82 |
| Sat | 38.20 | 51.34 | 2.37 | 2.31 | 97.70 | 96.12 |
本文在最大化向量夹角间隔分类器的基础上,提出了求解最优向量的不同方法,即使得最优向量最大限度的接近正类样例的中心和负类样例的中心,得到中心向量夹角间隔分类器.进而建立中心向量夹角间隔分类器与包围球的关系,训练大规模数据集.但鉴于包围球的结构严重依赖于调和参数,又提出了正则化核向量机,与中心向量夹角间隔分类器结合得到中心向量夹角间隔正则化核向量机.实验结果表明,中心向量夹角间隔分类器的分类精度和训练时间均优于之前的最大化向量夹角间隔分类器.中心向量夹角间隔正则化核向量机的训练时间和测试时间均短于最大化向量夹角间隔核向量机,并且测试精度高于最大化向量夹角间隔核向量机,即中心向量夹角间隔正则化核向量机可以有效快速地训练大规模数据集.
| [1] | Cortes C, Vapnik V N. Support vector networks[J]. Machine Learning, 1995, 20(3): 273-297. |
| [2] | Chang C C, Lin C J. Training v-support vector classifiers: Theory and algorithms[J]. Neural Computation, 2002, 13(9): 43-54. |
| [3] | Marizio M D, Taylor C C. Kernel density classification and boosting: An L2 analysis[J]. Statistics and Computing, 2005, 15(2): 113-123. |
| [4] | 陶新民, 曹盼东, 宋少宇, 等. 基于半监督高斯混合模型核的支持向量分类算法[J]. 信息与控制, 2013, 42(1): 18-26. Tao X M, Cao P D, Song S Y, et al. The SVM classification algorithm based on semi-supervised Gauss mixture model kernel[J]. Information and Control, 2013, 42(1): 18-26.. |
| [5] | Tax D M J, Duin R P W. Support vector data description[J]. Machine Learnings, 2004, 54(1): 45-66. |
| [6] | Wu M R, Ye J P. A small sphere and large margin approach for novelty detection using training data with outlier[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2009, 31(11): 2088-2092. |
| [7] | Takahashi N, Nishi T. Rigorous proof of termination of SMO algorithm for support vector machines[J]. IEEE Transactions on Neural Networks, 2005, 16(3): 774-776. |
| [8] | Smola A, Scholkopf B. Sparse greedy matrix approximation for machine learning[C]//Proceedings of the 17th International Conference on Machine Learning. New York, NJ, USA: ACM, 2000: 911-918. |
| [9] | Achlioptas D, McSherry F, Scholkopf B. Sampling techniques for kernel methods[C]//The 2001 Conference on Advances in Neural Information Processing Systems. 2002: 335-342. |
| [10] | Fine S, Scheinberg K. Efficient SVM training using low-rank kernel representations[J]. Journal of Machine Learning Research, 2001, 2(2): 243-264. |
| [11] | Tsang I W, Kwok J T, Cheung P M. Core vector machine: Fast SVM training on very large data sets[J]. Journal of Machine Learning Research, 2005, 6(2): 363-392. |
| [12] | Tsang I W, Kwok J T, Zurada J M. Generalized core vector machines[J]. IEEE Transactions on Neural Networks, 2006, 17(5): 1126-1140. |
| [13] | Hu W J, Chung F L, Wang S T. The maximum vector-angular margin classifier and its fast training on large datasets using a core vector machine[J]. Neural Networks, 2012, 27(3): 60-73. |
| [14] | Wang C D, Lai J H. Position regularized support vector domain description[J]. Pattern Recognition, 2013, 46(3): 875-884. |
| [15] | Hu W J, Chung F L, Wang S T, et al. Scaling up minimum enclosing ball with total soft margin for training on large datasets[J]. Neural Networks, 2012, 36(8): 120-128. |
| [16] | Chung F L, Dend Z H, Wang S T. From minimum enclosing ball to fast fuzzy inference system training on large datasets[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(1): 173-184. |
| [17] | Deng Z H, Chung F L, Wang S T. FRSDE: Fast reduced set density estimator using minimal enclosing ball approximation[J]. Pattern Recognition, 2008, 41(4): 1363-1372. |



