1 引言
基于LCMV准则的波束形成算法能够有效提高阵列信号处理系统的性能,但是,该算法需要准确知道期望信号方向,进而对波束方向进行约束. 若约束方向偏离期望信号的实际方向,则期望信号会被误认为是干扰,并在该方向上形成零陷,对算法性能造成极大影响.
针对LCMV算法对导向矢量误差敏感这一问题,许多学者在提高LCMV算法鲁棒性方面做出了研究. 文[1, 2, 3]提出了基于特征空间分解的LCMV算法,该算法的权矢量是由LCMV波束形成器的最优权矢量向信号相关矩阵特征空间作投影得到的,该算法有效地减少了算法的计算量,且使波束具有更好的信噪比和稳健性,但当指向误差较大时,算法的性能明显变差. 文[4]对此提出一种改进方法,该算法主要利用阵列接收数据来校正算法中的约束导向矢量,使该导向矢量尽可能地接近期望信号的导向矢量,从而提高波束形成的性能. 为了节约特征值分解所需的时间,文[5, 6]提出一种简化的特征空间分解方法,该方法利用空间协方差矩阵构建一个信号子空间,无需特征分解,大大降低了计算量. 另一种较为常见的改进方法是对角加载类方法,文[7]结合对角加载量与LCMV算法,有效地增强了算法的稳健性,但它需要凭经验来确定对角加载量的值. 对此,文[8, 9]根据自相关阵特征向量中与期望信号导引向量相关性最大的特征向量所对应的特征值来调整加载值,使得算法形成特性良好的方向图,但算法计算量较大. 文[10]提出了一种基于广义线性组合(generalized linear combination,GLC)的全自动计算对角加载值的改进算法,该算法无需提前给出任何参数,具有较强的鲁棒性.
为了降低LCMV算法的运算量,文[11, 12]采用递归最小二乘(recursive least squares,RLS)算法来避开LCMV中的逆矩阵计算并降低了运算量,但在快拍数较低时,算法对噪声抑制效果较差. 同为迭代计算最优权矢量的LMS算法,其收敛速度虽然较RLS算法慢,但是其计算复杂度要低得多. 因此,文[13]提出一种递归搜索最优权矢量的方法,该方法采用基于梯度搜索的最优化算法计算导向矢量,在有效减小LCMV算法运算量的同时,使算法对导向矢量误差具有较好的稳健性. 文[14, 15, 16, 17]则通过变步长的方法提高LMS算法的收敛速度. 文[18]利用最陡下降法递归搜索最优权矢量和约束导向矢量,该算法能够同时兼顾指向误差、 阵元位置误差以及相位误差对算法性能的影响.
本文提出了一种改进的LCMV-LMS波束形成方法,采用信号的4阶累积量估计导向矢量,避免人为设定导向矢量,提高算法自适应性; 采用变步长LMS方法避免常规LCMV中矩阵求逆运算; 通过迭代更新LMS算法中的步长,使得算法具有较快的收敛速度和较小的输出稳态误差.
2 阵列信号模型设有M个远场窄带信号分别从方向(θ1,θ2,…,θM)入射到由N个阵元组成的线阵上,其阵元间距为d,则阵列接收数据可表示为
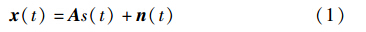
其中,x(t)为t时刻阵列的接收数据,x(t)=[x1(t),x2(t),…,xN(t)]; A为阵列的流形矩阵,A=[a(θ1),a(θ2),…,a(θM)],其中,a(θm)为θm方向信号的导向矢量; s(t)是t时刻接收信号的复包络; n(t)为t时刻接收的噪声矢量,本文的仿真过程中采用的是高斯噪声.
若将窄带波束形成器的加权向量表示为ω=[ω1,ω2,…,ωN]T,其中,ωn为第n个阵元对应的加权值. 则经波束形成器后的输出信号加权和表示为

阵列接收数据的协方差矩阵可表示为
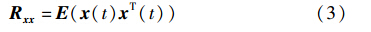
阵列输出总功率为
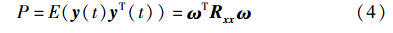
3 LCMV-LMS算法简介
LCMV算法是在输出功率P最小情况下的波束形成,即:

约束条件为

其中,(θ1)为期望信号的假设导向矢量,θ1为假设的来波方向.
LCMV算法的代价函数写为

对J(ω)关于ωT求导,得到权矢量搜索过程中的梯度矢量:
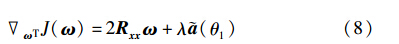
因此,最优权矢量ωopt为

其中,λ=(T(θ1)R-1xx(θ1))-1.
为避免式(8)中的求逆运算,LCMV-LMS算法迭代求得最优权矢量:
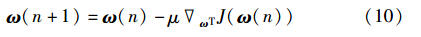
其中,μ为权矢量ω的迭代步长.
由文[7]可知,LCMV-LMS波束形成法不具备预测来波方向的功能,若假设的导向矢量与真实导向矢量之间存在误差,波束的主瓣将对准假设的导向,真正的目标信号将有可能被视为干扰而被抑制掉,这会导致自适应波束形成的信噪比(signal to noise ratio,SNR)降低.
Widrow等[19]在研究LMS算法收敛性时,总结出其稳态误差S为

到达稳态后的S值越大,则算法的稳态误差越大. 由式(11)可见,稳态误差S与步长μ成正比. 因此,固定步长的LCMV-LMS算法不能兼顾收敛速度和稳态误差两方面的性能.
4 改进的自适应LCMV-LMS算法
4.1 自适应导向矢量估计
为了自适应地得到期望信号的真实导向矢量,本文采用了基于接收信号4阶累积量的导向矢量估计方法.
设接收信号的4阶累积量为C=[C1,C2,…,CN]T. 其中,Cn为第n个阵元所对应的接收信号4阶累积量,N为阵元数,即:
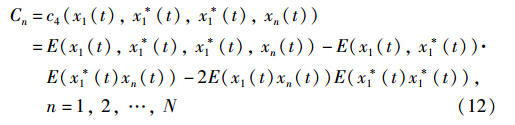
其中,xn(t)=an(θ1)sn(t)+nn(t),xn(t)为t时刻第n个阵元的接收信号,an(θ1)是第n个阵元对θ1方向目标的导向,nn(t)是第n个阵元接收到的噪声,c4(·)代表求4阶累积量.
4阶累积量具有可加性,且高斯噪声的4阶累积量为0,因此:
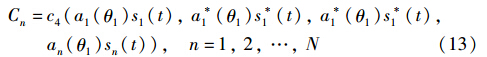
根据4阶累积量的性质可知:
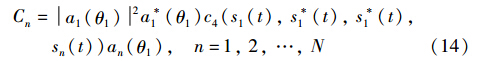
令β=[β1,β2,…,βN],且:

则Cn=βnan(θ1)且C=β·a(θ1). 由此可知,第n个阵元对θ1方向目标的估计导向值n(θ1)为

对θ1方向目标的估计导向矢量(θ1)为(θ1)=[1(θ1),2(θ1),…,N(θ1)]. 将期望信号导向矢量由(θ1)替换,则:
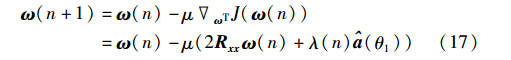
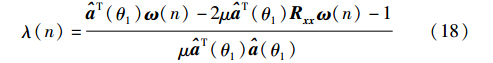
4.2 自适应改变步长参数
为兼顾算法的收敛速度和稳态误差,本文提出一种基于标准正态分布函数的变步长方法. 基本思想是: 当单步的权矢量远离最优权矢量时,选用大步长以提高算法收敛速度; 当单步的权矢量接近最优权矢量时,选用小步长以此提高收敛精度.
迭代开始时,根据文[19],设定步长最大值的更新公式μmax(n)为
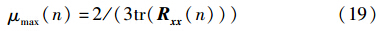
其中,tr(·)表示矩阵的迹. 为了满足自适应设置迭代步长的需求,本文引入关系式:
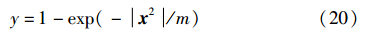
图 1为式(20)的函数曲线.
 |
| 图 1 m值不同时式(20)的函数曲线Fig. 1 Function curves of the equation (20) with different m |
对式(8)中梯度矢量求欧氏范数的平方,得:
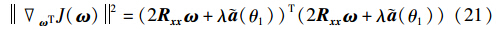
变量 ωTJ(ω)2减小得越慢,则LCMV-LMS算法迭代到最优权矢量的时间越长,即算法的收敛速度越慢; 其减小得越快,代表算法的收敛速度越快. 若假设式(20)中的变量x为梯度矢量 ωTJ(ω)的欧氏范数平方 ωTJ(ω)2,变量y为归一化的迭代步长,则由图 1可知, ωTJ(ω)2与迭代步长之间的关系满足变步长的基本思想,而且步长的变化速度随着参数m的减小而加快.
本文引入前后两步 ωTJ(ω)2的比值作为参数m的更新式,即:
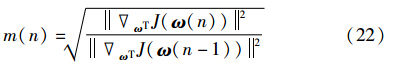
这样,当迭代的权矢量接近最优权矢量时,随着 ωTJ(ω)2变化的减小,步长的变化减慢,稳态误差减小. 因此,步长的更新公式表示为
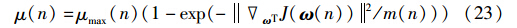
将本文提出的算法称为“4阶累积量的变步长LCMV-LMS(简称CUM-LCMV-VLMS)算法”.
5 仿真实验结果与分析
5.1 实验的主要步骤
步骤1 设置阵元数N,快拍数Q.
步骤2 设置θ1方向期望信号的导向矢量的初始估计值为(θ1)=0.
步骤3 (1) 根据式(14)计算接收信号的4阶累积量Cn; (2) 根据式(15)计算变量βn; (3) 根据式(16)计算相对于第n个阵元,期望信号的导向估计值n(θ1); (4) 重复步骤3中的(1)~(3),直至n=N; (5) 输出导向矢量的估计值(θ1).
步骤4 设置加权矢量初始值ω(1)=0,初始的信号协方差矩阵Rxx(1)=x(1)xT(1),初始步长μ(1)=2/(3tr(Rxx(1))),变量λ(1)=0.
步骤5 (1) 根据式(18)更新参数λ(n); (2) 根据式(17)更新权矢量ω(n); (3) 根据式(23)更新步长μ(n); (4) 更新协方差矩阵[14]: Rxx(n+1)=1-1nRxx(n)+1nx(n)xT(n); (5) 重复步骤5(1)~5(4),直至n=Q; (6) 输出最终迭代出的权矢量ω.
5.2 实验结果与分析本文均以16阵元等间距线阵为例,信噪比SNR=0 dB,快拍数Q=1 000次,分别对算法的归一化方向图、 收敛特性及稳态误差特性进行仿真.
实验1 图 2、 3为分别采用LCMV、 LCMV-LMS和CUM-LCMV-VLMS算法对0°、 20°和60°方向目标的归一化方向图. 图 2中假设导向矢量与真实信号的导向矢量相同,图 3中假设导向比真实信号的导向偏大5°.
 |
| 图 2 无导向矢量误差时的归一化方向图Fig. 2 Normalized pattern without steering vector error |
从图 2可以看出,无导向矢量误差时,3种算法的方向图均能正确地指向目标所在方向,但LCMV算法的旁瓣很高,甚至在-23°左右处形成一个接近主瓣高度的旁瓣. 将该波束形成方法用于目标探测时,这一方向的高旁瓣会被误认为是有目标,对目标识别有着严重的影响. LCMV-LMS算法与本文算法则能够有效的抑制旁瓣,其中本文算法具有更低的旁瓣.
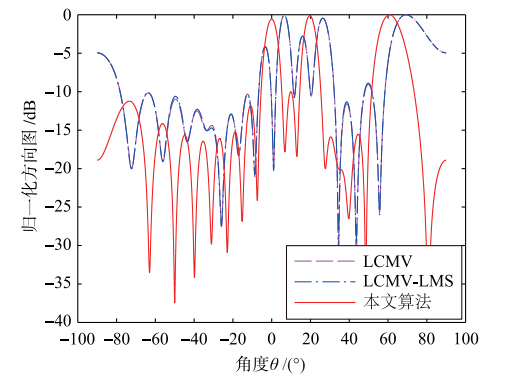 |
| 图 3 存在5°导向误差时3种算法的归一化方向图Fig. 3 Normalized pattern of the three algorithms with 5° steering vector error |
从图 3可以看出,当前两种算法的假设导向与真实导向存在误差时,它们的波形几乎重合且都指向错误的假设导向,在真实导向0°、 20°和60°处形成零陷,即将真实信号当作噪声抑制掉,并且主瓣之间的旁瓣过高,将波束形成应用于超声成像时,图像的对比度降低,增加了图像识别的难度.
本文算法无需设置假设导向,自适应地估计出信号导向,其方向图能够较为准确地指向目标的方向,旁瓣抑制效果较好.
实验2 图 4为LCMV-LMS与本文算法对20°方向目标的归一化方向图,假设的导向比真实导向偏大5°. 图 5为LCMV-LMS与本文算法迭代过程中的输出信噪比曲线.
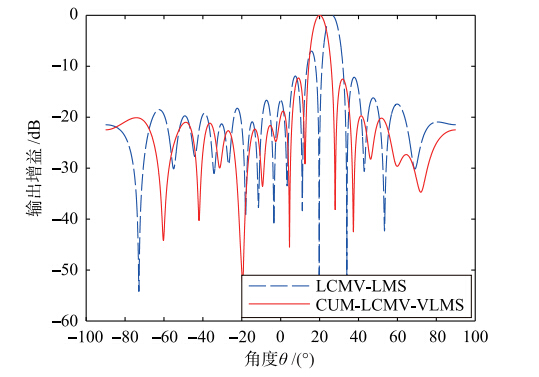 |
| 图 4 存在5°导向误差时本文方法与LCMV-LMS算法的归一化方向图Fig. 4 Normalized pattern of the proposed algorithm and the LCMV-LMS algorithm with 5° steering vector error |
图 4中,LCMV-LMS算法的方向图偏离目标方向5°,本文算法的方向图能够较为准确地指向目标方向20°. 对应图 5中的SNR曲线,LCMV-LMS算法达到稳态时,其信噪比较标准值下降约8 dB,而本文算法仅下降约3 dB.
 |
| 图 5 输出信噪比随迭代次数变化曲线Fig. 5 Curves of output SNR with the change of iterations |
实验3 图 6和图 7为LCMV-LMS、 固定步长CUM-LCMV-LMS和本文算法的 ωTJ(ω)2曲线. 图 6中,前两种算法取最大步长[8]μmax=2/(3tr(Rxx))=0.020 9. 图 8中,作为对比,保持第1种算法为最大步长不变,将第2种算法的步长降为0.01. 图 8和图 9分别为与图 6和图 7对应的稳态误差曲线.
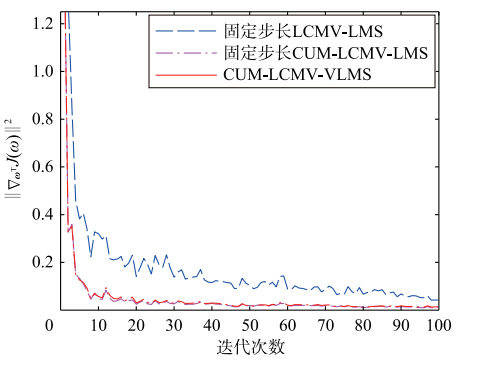 |
| 图 6 μmax=0.020 9时3种算法 ωTJ(ω)2曲线对比Fig. 6 Comparison of ωTJ(ω)2 curves among the three algorithms while μmax=0.0209 |
从图 6和图 7可以看出,即使固定步长设定为最大值,第1种算法的收敛速度仍然较慢,第2种算法与本文算法收敛速度较快,说明本文算法具有最大步长的收敛速度. 而当第2种算法的步长减小时,其收敛速度明显下降. 稳态时的 ωTJ(ω)2可表示为
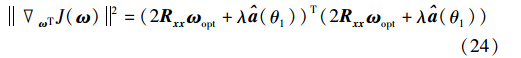
从图 8和图 9可以看出,最大步长的前两种算法具有
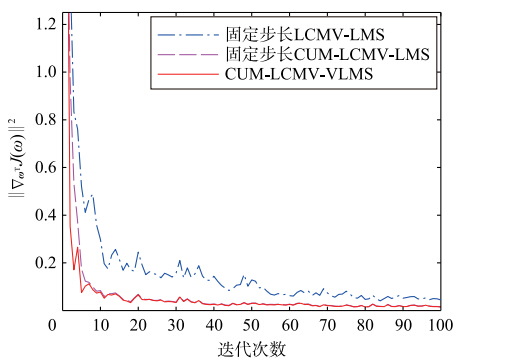 |
| 图 7 μ=0.01时3种算法的 ωTJ(ω)2曲线对比Fig. 7 Comparison of ωTJ(ω)2 curves among the three algorithms while μ=0.01 |
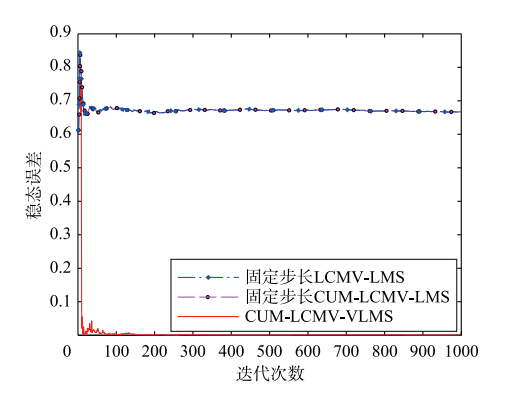 |
| 图 8 μmax=0.020 9时3种算法稳态误差曲线对比Fig. 8 Comparison of steady-state error curves among the three algorithms while μmax=0.0209 |
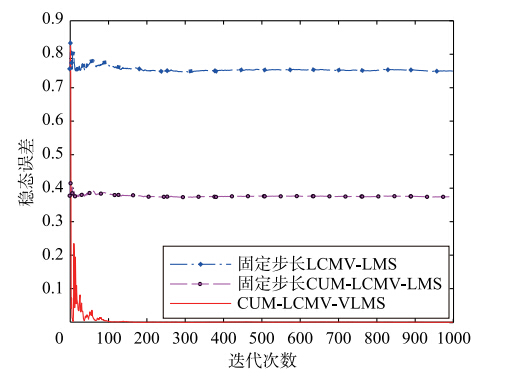 |
| 图 9 μ=0.01时3种算法的稳态误差曲线对比Fig. 9 Steady-state error curves of the three algorithms while μ=0.01 |
几乎相同的稳态误差曲线,当第2种算法的固定步长减小时,其稳态误差降低. 本文算法具有更接近于0的稳态误差. 除此之外,不同步长对应的收敛性能如表 1所示. 可以看出,本文算法无需设定步长且稳态误差很小,达到稳态所需的迭代次数也较少. 在迭代过程中,本文算法的自适应步长最大值为0.020 9,最小值为2.531 5×10-6.
| LCMV-LMS算法 | CUM-LCMV-LMS算法 | 本文算法 | |||||
| 步长μ | 0.020 9 | 0.01 | 0.005 | 0.020 9 | 0.01 | 0.005 | — |
| 稳态误差S | 0.666 8 | 0.318 8 | 0.160 7 | 0.666 7 | 0.322 4 | 0.163 8 | 0.946 9×10-3 |
| 迭代次数 | 33 | 53 | 61 | 6 | 10 | 18 | 13 |
本文针对LCMV算法对导向矢量误差敏感、 求逆运算量较大及自适应性能差的问题,提出了一种基于信号4阶累积量的变步长LCMV-LMS算法. 该算法能够对导向矢量进行预测,较为准确地估计出来波方向,具有较强的自适应测向能力; 能够迭代求解最优权矢量,避免信号相关矩阵求逆运算,降低运算复杂度; 能够自适应改变迭代步长,平衡算法收敛速度和稳态误差两方面性能. 实验证明,本文提出的算法具有良好的自适应性能.
| [1] | Chang L, Yeh C C. Effect of pointing errors on the performance of the projection beamformer[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(8): 1045-1056. |
| [2] | Lee C C, Lee J H. Eigenspace based adaptive array beamforming with robust capabilities[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(12): 1711-1716. |
| [3] | 廖桂生, 保铮, 张林让. 基于特征结构的自适应波束形成新算法[J]. 电子学报, 1998, 26(3): 23-26. Liao G S, Bao Z, Zhang L R. A new eigenstructure-based algorithm for adaptive beamforming[J]. Acta Electronica Sinica, 1998, 26(3): 23-26. . |
| [4] | 张林让. 自适应阵列处理稳健方法研究[D]. 西安: 西安电子科技大学, 1998. Zhang L R. Steady method research of adaptive array signal processing[D]. Xi'an: Xi'an Electronic and Engineering University, 1998.. |
| [5] | 闫冰冰, 代月花, 陈军宁, 等. 一种简化特征空间稳健自适应波束形成算法[J]. 计算机应用研究, 2011, 28(11): 4057-4059. Yan B B, Dai Y H, Chen J N, et al. Simplified eignspace-based robust adaptive beamforming algorithm[J]. Application Research of Computers, 2011, 28(11): 4057-4059.. |
| [6] | 赵宏鹏, 代月花, 朱德智, 等. 一种稳健的波束域自适应波束形成算法[J]. 计算机应用技术, 2014, 31(4): 1151-1153. Zhao H P, Dai Y H, Zhu D Z, et al. Robust neam-space adaptive beamforming algorithm[J]. Application Research of Computers, 2014, 31(4): 1151-1153. . |
| [7] | Li J, Stoica P, Wang Z. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715. |
| [8] | 程春悦, 吕英华. 基于可变对角加载的自适应波束形成算法[C]//通信理论与信号处理新进展——2005年通信理论与信号处理年会论文集. 北京: 电子工业出版社, 2005: 209-212. Cheng C Y, Lu Y H. Adaptive beamforming algorithm based on the variable diagonal loading[C]//New Progress of Communication Theory and Signal Processing-2005 Essays of Communication Theory and Signal Processing. Beijing: Publishing House of Electronics Industry, 2005: 209-212.. |
| [9] | 程春悦, 吕英华. 改进LCMV算法在抑制干扰噪声中的应用[J]. 电子测量与仪器学报, 2006, 20(4): 29-32. Cheng C Y, Lu Y H. Application of improved LCMV algorithm in restraining interference and noise[J]. .Journal of Electronic Measurement and Instrument, 2006, 20(4): 29-32 . |
| [10] | 张海滨, 曲强, 金明录. 一种改进的基于可变加载的鲁棒波束形成算法[C]//2010年通信理论与信号处理学术年会论文集. 北京: 电子工业出版社, 2010: 360-366. Zhang H B, Qu Q, Jin M L. An improved robust adaptive beamforming algorithm based on variable loading[C]//2010 Academic Essays of Communication Theory and Signal Processing. Beijing: Publishing House of Electronics Industry, 2010: 360-366. . |
| [11] | Li Z L, Han Z R, Deng L G. Research on an new RLS-LCMV beamforming algorithm with robustness[C]//4th IEEE International Conference on Wireless Communications, Networking and Mobile Computing. Piscataway, NJ, USA: IEEE, 2008: 1-3. |
| [12] | 刘广钟, 夏晓丽. 水声通信中RLS-LCMV波束形成算法的研究[J]. 现代电子技术, 2011, 34(21): 89-91. Liu G Z, Xia X L. Research on RLS-LCMV beamforming algorithm in underwater communication[J]. Modern Electronics Technique, 2011, 34(21): 89-91.. |
| [13] | 邓欣, 廖桂生, 刘宏清. 递归的稳健LCMV波束形成算法[J]. 系统工程与电子技术, 2007, 29(3): 449-452. Deng X, Liao G S, Liu H Q. Recursive robust LCMV beamforming algorithm[J]. Systems Engineering and Electronics, 2007, 29(3): 449-452.. |
| [14] | 孙恩昌, 李于衡, 张冬英, 等. 自适应变步长LMS滤波算法及分析[J]. 系统仿真学报, 2007, 19(14): 3172-3175. Sun E C, Li Y H, Zhang D Y, et al. Adaptive variable-step size LMS filtering algorithm and its analysis[J]. Journal of System Simulation, 2007, 19(14): 3172-3175. . |
| [15] | 张会芝, 穆晓霞, 王鲜芳. 一种新变步长LMS算法及在自适应波束形成中的应用[J]. 测控技术, 2014, 33(1): 129-132. Sun H Z, Mu X X, Wang X F. A new variable step LMS algorithm and its application in adaptive beamforming[J]. Measurement and Control Technology, 2014, 33(1): 129-132. . |
| [16] | 倪宁, 李京华, 王景. 基于新的变步长模型的LMS自适应滤波算法[J]. 现代电子技术, 2011, 34(10): 91-94. Ni N, Li J H, Wang J. LMS adaptive filtering algorithm based on novel variable step size model[J]. Modern Electronics Technique, 2011, 34(10): 91-94. . |
| [17] | 亢润东, 宋国强. 基于S形函数的变步长LMS算法[J]. 无线电工程, 2013, 43(11): 29-32. Hang R D, Song G Q. Variable step-size LMS algorithm based on sigmoid function[J]. Radio Engineering, 2013, 43(11): 29-32. . |
| [18] | 燕飞, 赵书敏. 基于最陡下降的稳健LCMV波束形成算法[J]. 计算机仿真, 2012, 29(6): 117-139. Yan F, Zhao S M. Robust LCMV beamformer algorithm based on steepest descent method[J]. Computer Simulation, 2012, 29(6): 117-139.. |
| [19] | Widrow B, McCool J M, Larimore M G, et al. Stationary and nonstationary learning characteristics of the LMS adaptive filter[J]. Proceedings of the IEEE, 1976, 64(8): 1151-1162. |



