1 引言
第三代蜂窝移动通信具有支持不同速率多媒体多业务(如语音、 音频、 视频、 数据包等)传输的特点. 针对这种多业务多速率传输的要求,CDMA提供了一种比较直接可靠的多速率解决方案,目前提出了多速率CDMA方法,主要包括可变切普速率(variable chip rate,VCR)技术、 可变扩频长度(variable spreading length,VSL)技术以及多子码(multi-code,MC)技术等,其中可变扩频长度多速率CDMA是一种比较有效的方法.
在非合作通信中,一些盲估计方法用来估计直扩信号的扩频序列,典型的方法包括特征值分解[1, 2, 3]、 基于子空间的方法[4, 5]、 盲源分离[6, 7, 8]以及期望最大化(EM)算法[9, 10]等. 这些方法对于一般的简单的直扩信号具有一定的效果,但对于多速率DS/CDMA信号不能直接应用. 对于多速率信号的参数盲估计问题值得去研究,文[11]利用多速率采样的方法估计出多速率CDMA扩频码片速率,文[12]利用波动相关(fluctuation of correlation)的方法估计出了多速率DS/CDMA扩频码周期,文[13]借鉴文[12]方法估计出了伪码周期具有整数倍数关系的多速率DS/CDMA以及多载波DS/CDMA的扩频码周期. 文[14]利用Frobenius范数结合特征值分解的方法估计出异步多速率DS/CDMA延迟以及扩频码序列. 文[15]利用FastICA[16]方法估计出扩频周期为整数倍数关系的多速率DS/CDMA的伪码序列. 该方法使用子空间的思想,以伪码周期循环地对数据分段估计出伪码序列,相对其它周期的伪码序列等效为虚拟用户,可以估计各用户伪码周期呈整数倍关系的伪码序列. 但是,各用户伪码周期是非整数倍关系时方法并不适用,这是由于伪码周期非整数倍关系按照主用户周期分段截取数据,除主用户外其它用户的信号已经失去了周期特征不能等效多个虚拟用户模型.
本文提出一种结合稳健JADE[17, 18]算法的多速率DS/CDMA信号扩频序列并行估计方法,克服了文[15]对伪码周期是非整数倍关系失效的缺陷,方法是以各个周期用户信号相互独立为依据的,与盲源分离方法独立性的要求一致,直接将信号建模为主用户和干扰用户的模型,即其它周期内所有伪码直接等效为一个干扰用户. 方法首先利用二次功率谱[19, 20]的方法估计出不同速率用户的扩频码周期,然后利用多速率DS/CDMA信号周期特性将信号按照周期建模为主用户和干扰用户模型,最后针对同步和异步两种情况,分别以单倍周期和两倍周期长度对数据进行分割,生成数据矩阵,并结合稳健的JADE盲源分离算法对扩频序列进行盲估计.
2 多速率DS/CDMA信号模型
考虑有效用户数为Nu的多速率DS/CDMA信号模型,将用户可利用的信息速率分为S组,且各个速率之间满足R1
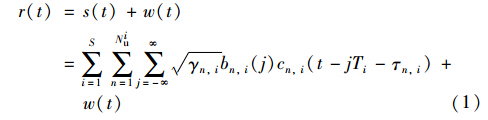
其中,γn,i、 bn,i(j)=±1( j∈Z)、 τn,i分别表示第i组速率群的第n个用户信号信息码符号、 幅度及延迟,cn,i(t)为第i组速率群的第n个用户扩频码波形,表示为

其中,{cn,i(l)=±1,l∈Z+}为扩频序列的取值,ψ(t)为矩形切普脉冲,且满足ψ(t)=1,0≤t≤Tc0,others,n(t)为零均值、 方差为σ2n的高斯白噪声. 图 1为3组速率的用户扩频的多速率模型.
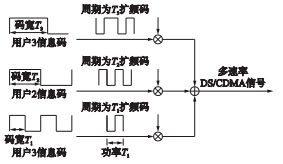 |
| 图 1 多速率DS/CDMA信号产生示意图Fig. 1 Diagrammatic sketch of multi-rate DS/CDMA signals generation |
不失一般性,作如下假设:
(1) 信号信息符号服从等概率分布,且用户之间的信息序列相互独立,即E{bn,i(k)bm,j(k)}=0(i≠j或n≠m).
(2) 扩频码片宽度Tc为已知,各个用户之间的扩频序列互不相关,即E{cn,i(k)cm,j(k)}=0(i≠j或n≠m).
(3) 系统的噪声由均值为0、 方差为σ2n的高斯白噪声组成,且噪声与信号相互独立.
(4) 假设各组速率的用户数已知或已被估计出.
3 理论分析
3.1 多速率DS/CDMA信号的扩频码周期估计
对于多速率DS/CDMA信号伪码周期的估计,文[5]利用波动相关(fluctuation of correlation)的方法估计出了多速率DS/CDMA扩频码周期. 二次功率谱方法能够有效地估计一般单速率的DS-CDMA信号的伪码周期,经过理论证明二次功率谱的方法也可以扩展到多速率DS-CDMA信号,先前已经做过这方面工作,这里对多速率DS/CDMA伪码周期二次功率谱估计方法作一下简单阐述.
多速率DS/CDMA信号接收信号已经由式(1)给出,对多速率信号s(t)先求一次功率谱Ss(f),其表达是为
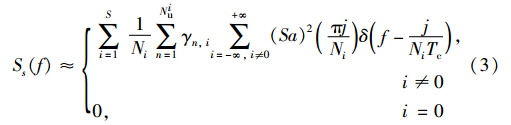
再对式(3)傅里叶变换并求模取平方求得二次谱:
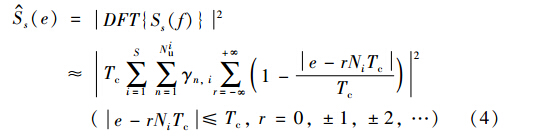
由式(4)的结果可以看出,当二次谱频率e=rNiTc(r=±1,±2,…),二次谱功率S^s(e)会产生一系列尖锐的谱线,该谱线间隔为扩频序列周期的整数倍(Sa倍),并且不同速率用户的二次谱谱线幅度是不同的,因此可以利用幅度区分各个速率并通过估计谱峰间隔求得各个速率伪码周期.
图 2为两组速率多用户信号二次谱示意图,扩频码选取周期255、 63的m序列,每组速率对应两个用户,其中采样率Sa=4. 图 2说明了利用二次谱估计能够准确地估计多速率DS/CDMA扩频码周期,从而为下文的并行建模的序列估计方法作铺垫. 由于该方法并不要求信号是同步的,因此无论同步还是异步方法均适用. 下面将利用已估计的周期进行扩频序列的估计,并针对同步和异步两种情况展开讨论.
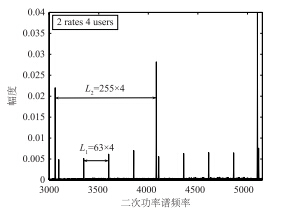 |
| 图 2 多速率DS/CDMA扩频码周期的盲估计Fig. 2 The blind estimation of spreading sequence periods of multi-rate DS/CDMA |
3.2 多速率DS/CDMA信号的并行建模方法
若将第q组速率(即扩频码周期为Tq)的扩频信号划分为一组,其余的v=S-q组速率的扩频信号以及噪声划分为一组,将式(1)等效为

其中,bq(t)=sv(t)+w(t)定义为干扰信号,由先前作出的假设,各个速率的用户扩频码以及信息码是统计独立,即在某种程度上可以将多速率DS/CDMA信号建模为由具有伪码周期为Tq的Nqu个主用户和与之相互统计独立的1个干扰用户构成,也即总用户个数为Nu的多速率DS/CDMA信号可以用Nqu+1个用户代替. 因而利用多速率信号周期特性实现扩频码序列的并行估计.
为了表述更清楚,对于依据不同周期划分时不同的建模方式其接收信号r(t)的表达式也相应地作出修改,并且对两者不作严格的区分,则:

图 3为多速率DS/CDMA信号并行建模的示意图.
3.3 多速率DS/CDMA信号扩频序列的并行估计以及JADE盲源分离算法基于以上的分析可知,可以依据周期特性将多速率DS/CDMA建模为主用户和干扰用户的模型,然而针对同步和异步信号需要作出不同的分段处理处理,下面针对两种情况分别进行分析.
 |
| 图 3 多速率DS/CDMA信号并行建模的示意图Fig. 3 Schematic diagram of multi-rate DS-CDMA signals′ parallel modeling |
3.3.1 同步多速率DS/CDMA
当考虑同步多速率DS/CDMA时,式(5)的延迟τn,i=0,则多速率表达式如下:
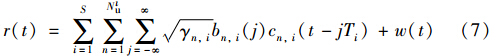
对信号进行采样,采样周期为Tc,其接收端信号离散形式为
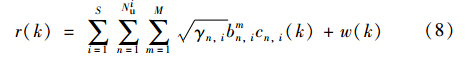
其中,bmn,i表示为第i组速率第n个用户的第m个信息码符号,cn,i(k)为第i组速率第n个用户的第k时刻扩频码符号,w(k)是高斯白噪声w(t)的离散形式. 以第q组速率的用户作为主用户,其余用户当作干扰用户建立模型,因此式(8)可以表示为
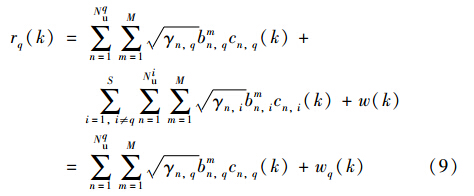
那么第m个信息符号的表达式为
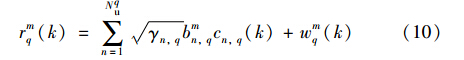
以单倍伪码周期Tq对数据进行分段,则写成向量的形式有:
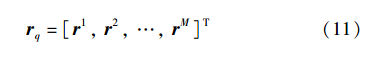
其中,

故将式(11)写成矩阵的形式有:
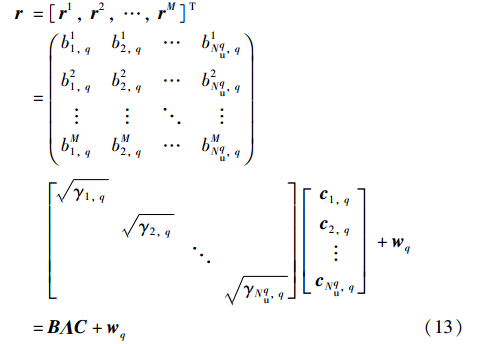

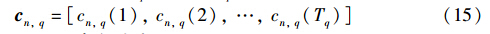
3.3.2 异步多速率DS/CDMA
对于式(5),当延迟τn,i≠0时,该模型为异步多速率模型,为了简化处理,这里认为τn,i=dn,iTc,其中dn,i=1,2,…,Ti,并且根据并行估计方法将扩频码周期为Tq的用户组作为主用户以及非Tq为周期的用户作为噪声,则异步信号表达式为

 |
| 图 4 异步多速率DS/CDMA信号的分割示意图Fig. 4 Diagrammatic sketch of the segmentation for asynchronous multi-rate DS-CDMA signals |
以采样周期为Tc进行采样,再以两倍主用户信息符号周期,重叠一倍信息符号周期进行数据分割生成数据矩阵,如图 4所示. 对应的第k个window分段表达式:
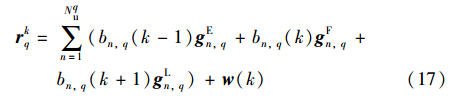
其中,w(k)为干扰用户. 第n个用户一个周期完整序列gn,q=[cn,q(1),cn,q(2),…,cn,q(Nn,q)]T,则gEn,q、 gFn,q、 gLn,q分别表示长度为2Nn,q且包含gn,q序列的后半部分、 中间部分以及前半部分的向量,表示如下:
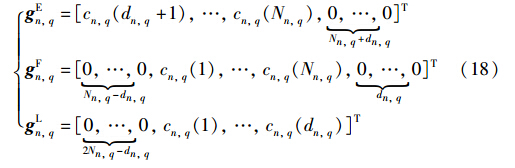
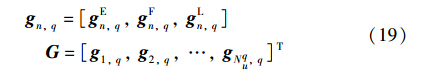
其中,式(18)中gFn,q包含了完整的用户伪码序列.
对于截取信号M个用户信息码长度的多速率DS/CDMA,则第q组速率第n个用户的信息码矩阵用AEn,q、 AFn,q、 ALn,q、 A表示,其表达式为
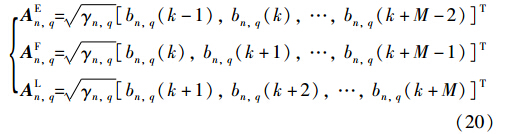
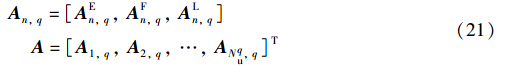
那么,可以得到多速率DS/CDMA信号矩阵表达式r为

其中w为干扰用户矩阵.
3.3.3 稳健的JADE盲源分离算法及多速率DS/CDMA扩频序列并行估计由前面两节关于同步和异步多速率DS/CDMA信号的分析可知,同步和异步模型的主要区别在于处理数据时分段的不同,同步是以单倍扩频周期长度对数据进行分段,异步是以两倍扩频码周期长度对数据进行分段,但是通过模型的确立,最终数据矩阵都可以写成两个矩阵的乘积的形式,如式(14)、 式(22)所示,这与盲源分离的模型相匹配,因此可以利用盲源分离的方法实现对多速率DS/CDMA扩频序列的估计.
考虑到JADE盲源分离算法具有良好的数值稳定性,以及对噪声具有一定稳健效果,这里采用JADE算法对多速率DS/CDMA扩频序列进行估计的步骤如下:
步骤1 白化
这里为了更好地对加性的高斯白噪声进行抑制,采用稳健的白化过程[17],得到白化后的观测信号,过程如下:
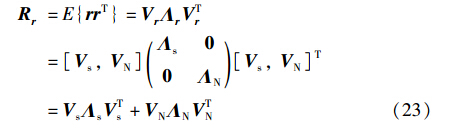
其中,Rr为r自相关矩阵,Vs、 VN分别表示信号子空间和噪声子空间,Λs=diag(λ1,λ2,…,λn)、 ΛN=diag(λn+1,λn+2,…,λm)分别表示为主特征值和噪声特征值构成的对角矩阵. 估计的噪声方差表示为2v=λn+1+λn+2+λmm-n,于是:


步骤2 特征矩阵联合近似对角化
(1) 选取一组M=[M1,M2,…,Mp](Mi均为N×N矩阵)计算M关于已白化的数据Z的4阶累积量矩阵QZ(Mi),其表达式为
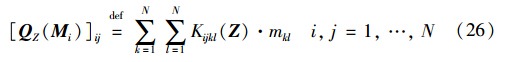
其中,Kijkl(Z)是矢量Z中第i,j,k,l 4个分量的4维累积量,mkl是矩阵M的第k行l列元素.
(2) 计算优化步骤求得酉矩阵V,使所有的QZ(Mi)联合对角化,即使式(27)DM(V)达到极小:
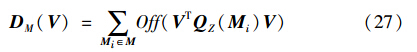
其中,Off(·)表示矩阵非对角元素平方求和运算. 得到分离后的矩阵y,即为对伪码序列的估计,其中:

上述算法中M得按照如下规律选取,将各个N×N矩阵Mi中的第p行q列个元素定义为
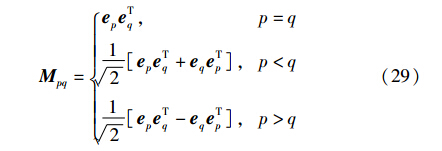
其中p,q=1,…,N,ep是除位置p处等于1外,其余位置都等于0的N×1单位矢量.
综上分析,对于同步和异步两种情况的多速率DS/CDMA信号扩频序列并行估计方法步骤归纳如下:
(1) 对截取的多速率DS/CDMA信号进行采样,并利用二次谱的方法估计所有伪码周期,记为T1,T2,…,TS.
(2) 按照周期Ti(i=1,2,…,S)对信号进行分段处理(同步情况下,以Ti长度分段; 异步时分段数据窗为2Ti,且重叠Ti)并按照式(11)和式(22)生成r数据矩阵.
(3) 确定分离用户个数: 若是同步情况下,分离用户数为Niu+1(其中Niu为周期为Ti的用户个数); 若是异步情况下,分离用户数为3Niu+1.
(4) 按照3.3.3节步骤,利用JADE算法对r进行盲分离,提取用户的扩频序列的估计值.
4 实验仿真为了验证本文算法在同步和异步情况下的有效性,做以下仿真实验:
实验1 同步多速率DS/CDMA信号扩频码序列的并行估计
当信噪比(signal noise ratio,SNR)SNR=-5 dB时,分别对两组速率的多速率DS/CDMA进行仿真,分别采用扩频码周期为31和63的m序列,处理数据为300×63 bit,且每组速率对应两个用户,如图 5所示.
从图 5(a)、 图 5(b)可以看出伪码序列并行估计按伪码周期为31或伪码周期为63进行数据分段并且用户数n=2,利用JADE算法进行盲源分离,会产生3个用户序列,其中2个序列为有用用户的序列,1个序列为干扰用户的序列,当作噪声源处理.
实验2 不同信噪比下正确估计扩频序列所需要的数据组数
为验证本文算法的性能,不同用户数随信噪比变化完全正确估计出所有伪码序列所需要的组数. 在信噪比为-16 dB~5 dB,采用扩频周期分别为255、 127、 63的m序列3组速率,依次为每组速率各1个用户,每组速率各2个用户,每组速率各3个用户以及每组速率各4个用户,采用并行估计方法对序列进行估计,估计序列每组数据长度127. 仿真结果如图 6所示.
 |
| 图 5 同步信号扩频序列的估计Fig. 5 Spreading sequence estimation of the synchronous signals |
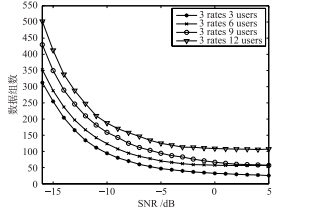 |
| 图 6 完全正确估计所有用户扩频序列所需要的数据组数的性能曲线Fig. 6 Performance curves of data numbers for estimating all users′ spreading sequences |
从图 6可以看出针对多个速率群的同步多速率DS/CDMA信号,算法是有效的,并且可以看出在速率组数、 用户数固定随着信噪比下降的条件下,实现正确的分离所需要的处理数据组数是增加的,同时从图 6看出在相同速率组数、 相同信噪比的条件下随着用户数的增加,需要的处理数据组数相应地增加.
实验3 同步多速率DS/CDMA信号不同速率组数不同信噪比的正确估计率
在图 7中,正确估计率等于正确估计次数除以蒙特卡洛仿真次数,从图 7可以看出速率组数、 用户数固定的情况下随着信噪比的降低,正确估计率下降,和仿真4.2结果吻合. 另外图 7表明了随着速率组数的增加,信噪比固定条件下,正确估计率相对降低.
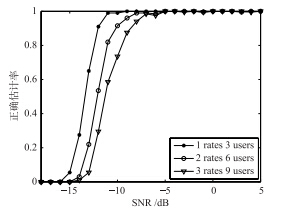 |
| 图 7 不同组速率不同信噪比的正确盲估计率Fig. 7 The correct ratio of the blind estimation for different group rates and different SNR |
实验4 异步多速率DS/CDMA信号扩频码序列的并行估计
为了验证本文算法对异步多速率DS/CDMA信号扩频码序列适用,采用两组速率信号,其伪码周期为127两个用户,延迟分别为30、 20,以及伪码周期为63的两用户,其延迟分别为20、 10,数据分割窗为254,且重叠127,进行仿真,结果如图 8所示. 图 8仿真结果表明对于异步的多速率DS/CDMA信号算法可行,同时说明当以伪码周期为127为主用户时,周期为63的用户以及噪声会当作干扰用户,并且算法两倍主用户伪码周期为分割窗进行的盲源分离,得到的用户数也会增加,2个用户通过分离算法会得到7个用户,而其中可以得出包含完整用户伪码的序列.
实验5 异步多速率DS/CDMA信号扩频码序列的并行估计性能仿真
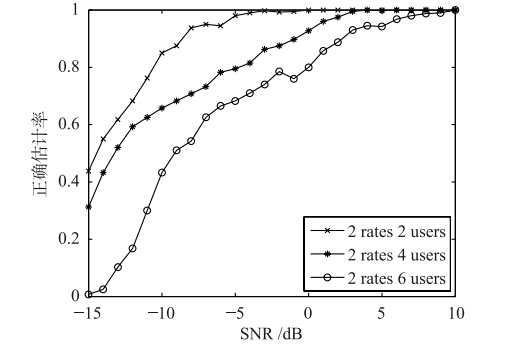
仿真采用两组速率,伪码周期为127、 63,总用户数分别为2、 4、 6的异步多速率DS/CDMA信号,异步延迟为随机生成,采用最大扩频码周期的两倍作为分割窗,应用本文算法,观察正确估计率、 信噪比以及用户数变化之间的关系. 仿真结果如图 9所示.
图 9看出异步多速率DS/CDMA信号在速率组数、 用户数固定条件下,正确估计率随信噪比降低而减小,当信
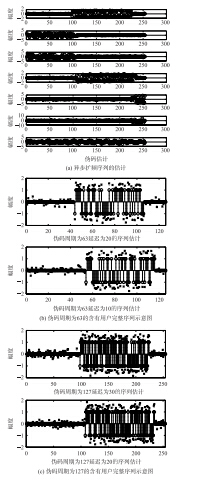 |
| 图 8 异步信号扩频序列的估计Fig. 8 Spreading sequence estimation of the asynchronous signals |
 |
| 图 9 不同信噪比下完全估计出所有用户序列的正确盲估计率Fig. 9 The correct ratio of the blind estimation of all users under different SNR |
噪比达到一定的程度时,正确估计率趋向1. 图 9同样说明随真实用户数的增加,分离算法会导致产生的虚拟用户成倍地增加,正确估计率变化较大.
实验6 伪码周期满足整数倍数多速率DS/CDMA两种方法的对照
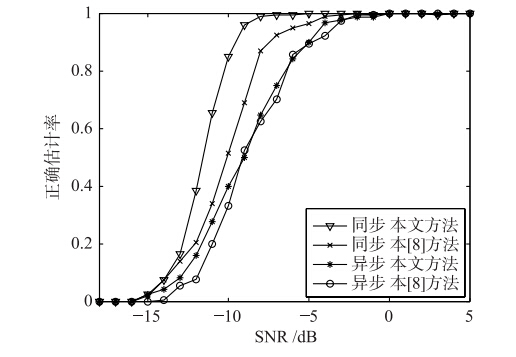
仿真分别采用具有两组速率的同步和异步的多速率信号,其伪码周期分别为128、 64,且每组速率包含两个用户,分别采用本文方法及文[8]方法进行伪码估计,蒙特卡洛仿真400次,并计算其正确估计率,结果如图 10所示.
 |
| 图 10 不同信噪比相同条件两种方法的对照Fig. 10 Comparison between two methods under different SNR |
5 结论
通过仿真分析,表明本文算法能在较低信噪比条件下实现对多速率DS/CDMA信号伪码序列的正确估计,并且适用于同步异步两种情况. 与文[8]相比,不仅可以估计各组速率伪码周期为整数倍数关系的多速率DS/CDMA的伪码序列,而且对各速率伪码周期为非整数倍的情况也适用. 另外,本文并行估计方法将多速率信号建模为主用户和干扰用户模型是基于信号源的独立性和信号的周期特性,这与盲源分离方法的独立性要求一致,方法具有一定的扩展性能.
| [1] | Gilles B, Cine B. Blind estimation of the pseudo-random sequence of a direct sequence spread spectrum signal[C]//21st Century Military Communications Conference. Piscataway, NJ, USA: IEEE, 2000: 967-970. |
| [2] | 张花国, 魏平. 基于恒模特性的QPSK-DSSS信号扩频序列的估计[J]. 航空学报, 2003, 34(6): 1389-1396. Zhang H G, Wei P. Spreading sequence estimation based on constant modulus property for QPSK-DSSS signals[J]. Acta Aeronautica Sinica, 2003, 34(6): 1389-1396. . |
| [3] | 张天骐, 周中正, 林孝康, 等. 低信噪比长伪码直扩信号的盲估计方法[J]. 信号处理, 2008, 24(3): 370-375. Zhang T Q, Zhou Z Z, Lin X K, et al. Approach to blind estimation of lower SNR long code DS signals[J]. Signal Proceesing, 2008, 24(3): 370-375.. |
| [4] | 张红波, 吕明. 基于子空间跟踪的扩频码盲估计算法[J]. 系统工程与电子技术, 2006, 28(10): 1470-1472. Zhang H B, Lü M. Blind estimation of PN sequence based on subspace tracking[J]. Journal of Systems Engineering and Electronics, 2006, 28 (10): 1470-1472.. |
| [5] | 侯瑞玲, 张天骐, 庞统, 等. 基于子空间的 DS-CDMA信号扩频序列估计技术[J]. 计算机应用研究, 2011, 28(2): 673-676. Hou R L, Zhang T Q, Pang T, et al. Spreading spectrum code estimation for DS-CDMA signal based on subspace[J]. Application Research of Computers, 2011, 28(2): 673-676. . |
| [6] | 付卫红, 杨小牛, 刘乃安. 基于盲源分离的CDMA多用户检测与伪码估计[J]. 电子学报, 2008, 36(7): 1319-1323. Fu W H, Yang X N, Liu N A. Muti-user detection and chip sequence estimation for CDMA system based on the blind source separation[J]. Acta Electronica Sinica, 2008, 36(7): 1319-1323.. |
| [7] | 高丽, 张天骐, 侯瑞玲, 等. 基于改进的EASI算法的DS-CDMA的信息码和伪码估计[J]. 电讯技术, 2012, 52(8): 1275-1279. Gao L, Zhang T Q, Hou R L, et al. Information and chip sequence blind estimation for DS-CDMA system based on improved EASI algorithm[J]. Telecommunication Engineering, 2012, 52(8): 1275-1279. |
| [8] | 任啸天, 徐辉, 黄知涛, 等. 基于FastICA的CDMA信号扩频序列优化盲估计[J]. 电子学报, 2012, 40(8): 1532-1538. Ren X T, Xu H, Huang Z T, et al. FastICA based optimize blind estimation of spreading sequence of CDMA signals[J]. Acta Electronica Sinica, 2012, 40(8): 1532-1538. . |
| [9] | Yao Y W, Poor H V. EM-based blind demodulation of synchronous CDMA[C]//2000 IEEE Sixth International Symposium on Spread Spectrum Techniques and Applications. Piscataway, NJ, USA: IEEE, 2000: 738-742. |
| [10] | Yao Y W, Poor H V. Blind detection of synchronous CDMA in non-Gaussian channels[J]. IEEE Transactions on Signal Processing, 2004, 52(1): 271-279. |
| [11] | Siavash G, Bahman A. Blind chip rate estimation in multirate CDMA transmissions using multirate sampling at slow flat fading channels[C]//2008 11th IEEE Singapore International Conference on Communication Systems. Piscataway, NJ, USA: IEEE, 2008: 1344-1348. |
| [12] | Nzeza C N, Gautier R, Burel G. Blind multiuser detection in multirate CDMA transmissions using fluctuations of correlation estimators [C]//Proceedings of the IEEE Global Telecommunications Conference. Piscataway, NJ, USA: IEEE, 2006: 1-5. |
| [13] | 沙志超, 吴海斌, 任啸天, 等. 非合作直扩信号检测的相关函数二阶距方法[J]. 系统工程与电子技术, 2013, 35(8): 160-164. Sha Z C, Wu H B, Ren X T, et al. Second-order moment of autocorrelation for signal detection in non-cooperative DS/SS communication[J]. Systems Engineering and Electronic, 2013, 35(8): 160-164.. |
| [14] | Nzeza C N, Gautier R, Burel G. Parallel blind multiuser synchronization and sequences estimation in multirate CDMA transmission[C]//2006 Fortieth Asilomar Conference on Signals, Systems and Computers. Piscataway, NJ, USA: IEEE, 2006: 2157-2161. |
| [15] | 任啸天, 徐晖, 黄知涛, 等. 基于盲源分离的Multi-Rate DS/CDMA信号扩频序列盲估计[J]. 航空学报, 2012, 33(8): 1455-1465. Ren X T, Xu H, Huang Z T, et al. Blind source separation based blind estimation of spreading sequences for multi-rate DS/CDMA signals[J]. Acta Aeronautica Sinica, 2012, 33(8): 1455-1465.. |
| [16] | Hwarinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634. |
| [17] | Cichocki A, Amari S. 自适应盲信号与图像处理[M]. 吴正国, 唐劲松, 章林柯, 等译. 北京: 电子工业出版社, 2005: 177-178. Cichocki A, Amari S. Adaptive blind signal and image processing[M]. Wu Z G, Tang J S, Zhang L K, et al Trans. Beijing: Publishing House of Electronics Industry, 2005: 177-178. |
| [18] | Pham D T, Cardoso J. Blind separation of instantaneous mixtures of non-stationary sources[J]. IEEE Signal Processing, 2001, 49(9): 1837-1848. |
| [19] | 张天骐, 张传武, 林孝康, 等. 直扩伪码周期及序列的估计算法[J]. 电波科学学报, 2001, 16(4): 518-521. Zhang T Q, Zhang C W, Lin X K, et al. Algorithm for period and sequence estimation of PN code in DS-SS signals[J]. Chinese Journal of Radio Science, 2001, 16(4): 518-521. |
| [20] | 张天骐, 代少升, 杨柳飞, 等. 在残余频偏下微弱直扩信号伪码周期的谱检测[J]. 系统工程与电子技术, 2009, 31(4): 777-781. Zhang T Q, Dai S S, Yang L F, et al. Method of spectra for periodic detection of the PN sequence in the weak DS-SS signals with residual carrier[J]. Journal of Systems Engineering and Electronics, 2009, 31(4): 777-781. . |



