1 引言
分数阶微积分的概念已经有300多年的历史,近年来随着在工程领域的广泛应用,已经引起控制界众多研究者的关注[1],如分数阶系统的稳定性分析[2]、 分数阶系统辨识[3]、 分数阶信号处理[4]、 分数阶控制器设计[5, 6]等,其中在分数阶控制器设计的研究中,最具代表性的当属Podlubny提出的分数阶PIλDμ控制器[7],在此基础上,文[8]针对常见的1阶时滞过程提出了分数阶PIλDμ控制器. 文[9, 10]针对一类分数阶系统,分别提出了一种FO-PD(fractional order proportional-derivative)控制器设计整定方法.
与整数阶PID(proportional-integral-derivative)控制器相比,分数阶PID控制器由于增加了微积分阶次参数,因此其整定的难度加大,目前主要的整定方法有Z-N法[11]、 稳定裕量法[12]、 稳定域内参数整定法[13]、 ITAE(integrated time and absolute error)指标最优法[14]等,但是这些方法都存在着复杂的运算. 另外,考虑系统参数摄动、 外界干扰等不确定性因素的影响以及对系统鲁棒性的要求,文[15]提出了基于输出反馈的分数阶(PI)γ和(PIDf)γ控制器的设计方法,该方法在改善系统动态响应性能的同时,保证了系统的鲁棒性.
内模控制是一种基于过程数学模型进行控制器设计的新型控制策略,由于它设计简单、 调整方便、 跟踪和控制性能好,因此得到广泛的应用. 将内模控制与分数阶控制相结合,不但保证系统良好的控制性能,而且有效地降低了分数阶控制器参数整定的复杂度.
本文针对常见的1阶系统、 2阶系统、 1阶加积分系统,根据内模控制原理设计了一种分数阶(PID)γ控制器,并基于系统的相位裕量(φm)和截止频率(ωc),实现了控制器参数的整定,该方法可在改善控制系统动态性能的同时,保证系统的鲁棒性.
2 分数阶微积分和分数阶PID控制器分数阶微积分的Riemann-Liouville(R-L)定义为: 若f(t)在[a,t]上连续可微,则R-L分数阶微分表示为
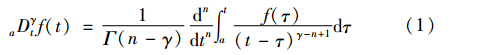
式中,a为初值,分数阶阶次γ满足n-1<γ
式中,若x为正整数,则Γ(x)=(x-1)!.
对式(1)进行拉普拉斯变换:
令L[f(t)]=F(s),在零初始状态下,式(3)中的求和项为零,则其可简化为
基于分数阶微积分的基础理论,Podlubny提出的分数阶PIλDμ控制器的传递函数为
式中,Kp、 Ki、 Kd分别为比例、 积分和微分增益,λ和μ分别为积分和微分阶次,且为大于0的实数.
在分数阶PIλDμ控制器的基础上,文[15]给出了一种改进型分数阶(PID)γ控制器,其传递函数为
式中,γ为分数阶积分阶次.
内模控制系统结构图如图 1所示,其中Q(s)为内模控制器,P(s)为被控过程,M(s)为过程模型,D(s)为过程的输入扰动,R(s)和Y(s)分别为系统的给定输入和输出.
根据内模控制原理,内模控制器Q(s)可按下式进行设计:
式中,M-(s)为过程模型中稳定的最小相位部分,f(s)为低通滤波器,本文采用以下形式:
式中,1<γ<2,η为滤波器时间常数.
图 1所示的内模控制系统可以等效为图 2所示的常规反馈控制系统,其中C(s)为等效反馈控制器.
C(s)和Q(s)有如下关系:
针对常见的1阶系统、 2阶系统和带积分的1阶系统,其传递函数分别如下:
式中,T、 T1和T2为时间常数,K为系统增益.
当系统模型精确时,即M(s)=P(s)且模型可逆,由式(7)和式(8)可得相应的内模控制器分别为
由式(9)得相应的反馈控制器分别为
可见式(16)~(18)均为分数阶(PID)γ控制器,该控制器仅包含η和γ两个可调参数,与式(5)和式(6)所示的分数阶PID控制器相比,为降低控制器整定的难度提供了可能.
在设计和分析控制系统时,鲁棒性总是首要关注的问题,因为用于控制器设计的模型往往不够精确,而且所有物理系统的参数常常会随着工作条件和时间而变化,这些因素总会使系统偏离设计要求,甚至使系统不稳定而无法正常工作. 稳定裕量φm是一个重要的鲁棒性指标,可以用来整定控制器参数,使其满足系统的性能要求.
开环系统可表示为
由稳定裕量和截止频率的基本理论可得系统开环传递函数G(s)的相位和幅值指标分别如下[9]:
式中,ωc为系统的截止频率.
另外,在截止频率ωc处,相位的导数为0,即:
基于式(10)和(16)、 式(11)和(17)、 式(12)和(18),得到系统的开环传递函数为
由式(23)可知,Arg(G(jω))=-γπ/2,且在截止频率ωc处,相位的变化率为0,即相位Bode图在对应截止频率附近有一个水平区域,闭环系统对增益的变化具有很强的鲁棒性. 基于式(20)和式(21)得
由式(24)和式(25)得:
如果给定系统的相位裕量φm和截止频率ωc的值,由式(26)可以得到控制器的参数γ和η.
为了验证本文方法的有效性,针对典型系统,利用Matlab对所提方法进行仿真分析,选择时间乘以误差绝对值积分(ITAE)和超调量(σ%)作为验证系统闭环性能的质量指标,并与现有的多种方法进行比较.
例1 考虑文[16]中的1阶系统模型:
由式(16)得分数阶(PI)γ控制器为
文[16]基于频域准则设计的分数阶PIλ控制器为
考虑比较的公平性,利用文[16]中给出的截止频率ωc=10 rad/s,相位裕量φm=60°,根据式(26)进行本文控制器参数整定,得γ=1.333 3和η=0.046 4. 设系统的设定值输入r(t)=1(t),输入扰动d(t)=-0.5(t-2),系统的单位阶跃响应曲线如图 3所示,系统的性能指标如表 1所示.
由图 3可见,本文方法和文[16]方法均表现出较好动态响应性能,但本文方法稳态无差,同时具有较强的干扰抑制特性. 同时表 1表明本文方法的系统性能指标均优于文[16]方法.
为了验证系统的鲁棒性,使系统参数T和K分别摄动20%和15%,即T=1.2,K=1.15,此时系统的单位阶跃响应曲线如图 4所示,由图 4和表 1可见当参数发生变化时,文[16]方法稳态误差增大,而本文方法具有更好的鲁棒性.
例2 考虑文[17]中的2阶系统模型:
由式(17)得分数阶(PID)γ控制器为
文[17]首先将此2阶系统模型降阶为1阶加时滞模型,然后将Bode理想传递函数作为期望特性设计了分数阶PIλ控制器为
同样根据文[17]给出的截止频率ωc=9.95 rad/s,并由γ=1.45和式(24)得相位裕量φm=49.5°,根据式(26)得η=0.035 7. 设系统的设定值输入r(t)=1(t),输入扰动d(t)=-0.5(t-4),系统的单位阶跃响应曲线如图 5所示,系统性能指标见表 2.
由图 5可见本文方法具有良好的动态响应性能,稳态无差,同时具有较强的抗干扰能力. 表 2表示本文方法的系统性能指标均优于文[17]方法.
当系统参数K、 T1和T2分别摄动30%、 20%和10%时,即K=1.3、 T1=0.24、 T2=1.32,系统的单位阶跃响应曲线如图 6所示. 由图 6和表 2可见当参数发生变化时,使用文[17]方法时系统的动态响应性能变差,稳态误差增大,本文方法则表现出更好的鲁棒性.
例3 考虑文[18]中直流电机位置伺服系统模型:
由式(18)得分数阶(PD)γ控制器为
文[18]基于系统稳定裕量设计分数阶PDμ控制器为
同样根据文[18]给出的截止频率ωc=10 rad/s,相位裕量φm=70°,根据式(26)进行本文控制器参数整定,得γ=1.222 2和η=0.06. 设系统的设定值输入r(t)=1(t),输入扰动d(t)=-1(t-5),系统的单位阶跃响应曲线如图 7所示,系统性能指标如表 3所示. 由图 7可见两种方法均具有良好的动态响应性能,但文[18]方法抗干扰能力较差. 表 3中本文方法的超调量略高于文[18]方法,但ITAE性能指标明显优于文[18]方法. 当系统的参数K和T分别摄动20%和10%时,即K=1.824、 T=1.44,系统的单位阶跃响应曲线如图 8所示. 由图 8和表 3可见,当参数发生变化时,文[18]方法表现出较差的干扰抑制特性.
6 结论
针对常见的1阶、 2阶、 1阶加积分系统,基于内模控制原理,采用分数阶滤波器代替整数阶滤波器给出了一种分数阶(PID)γ控制器的设计方法,并根据系统的稳定裕量,实现了分数阶控制器参数的整定,保证了系统的鲁棒性. 仿真结果表明所提方法设计简单,整定方便,可使系统获得良好的动态响应特性和克服系统参数变化的鲁棒性.

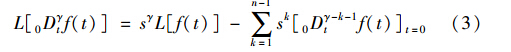


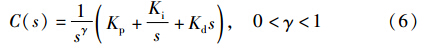

图 1 内模控制结构Fig. 1 Structure of IMC 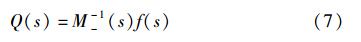


图 2 等效内模控制结构Fig. 2 Equivalent structure of IMC 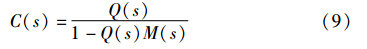

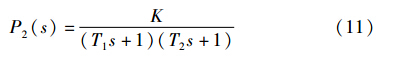


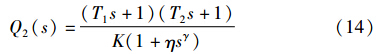
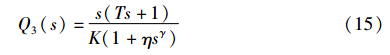
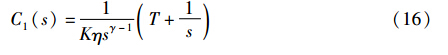
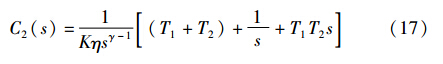


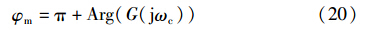
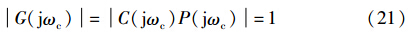



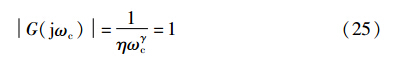


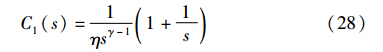

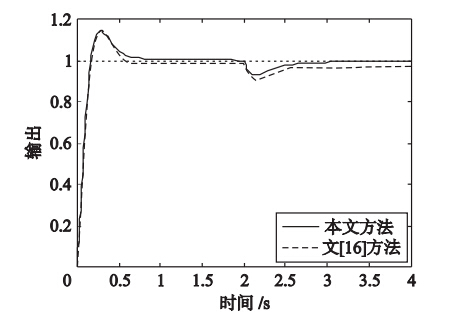
图 3 例1标称系统的单位阶跃响应Fig. 3 Unit step response of the nominal system for example 1 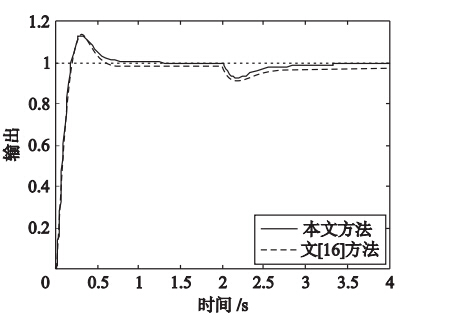
图 4 例1摄动系统的单位阶跃响应Fig. 4 Unit step response of the perturbation system for example 1 
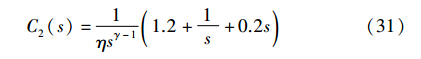
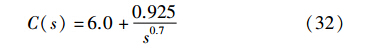
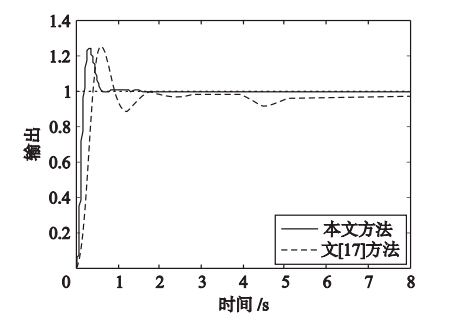
图 5 例2标称系统的单位阶跃响应Fig. 5 Unit step response of the nominal system for example 2 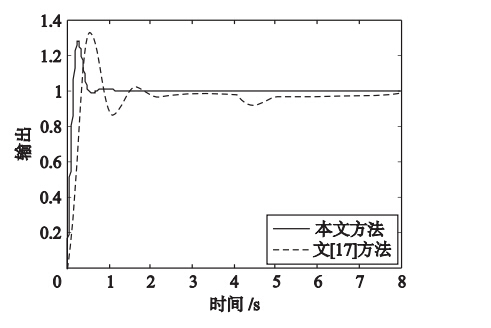
图 6 例2摄动系统的单位阶跃响应Fig. 6 Unit step response of the perturbation system for example 2 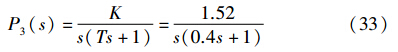


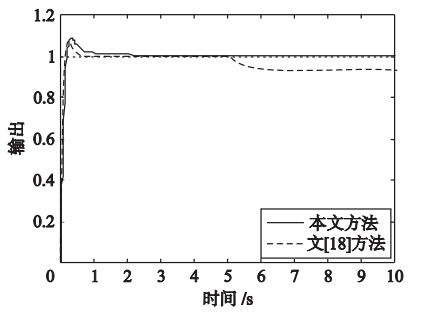
图 7 例3标称系统的阶跃响应曲线Fig. 7 Unit step response of the nominal system for example 3 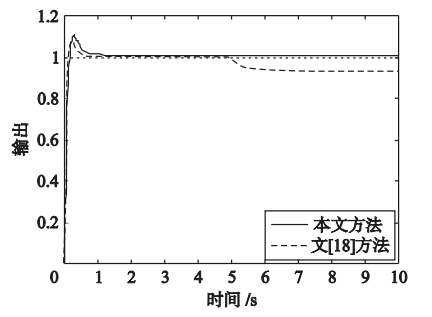
图 8 例3摄动系统的单位阶跃响应Fig. 8 Unit step response of the perturbation system for example 3
| [1] | Monje C A, Chen Y Q, Vinagre B M. Fractional-order systems and controls: Fundamentals and applications[M]. Berlin, Germany: Springer Verlag, 2010. |
| [2] | Lu J G, Chen Y Q. Robust stability and stabilization of fractional-order interval systems with the fractional order: The 0< α< 1 case[J]. IEEE Transactions on Automatic Control, 2010, 55(1): 152-158. |
| [3] | 廖增, 彭程, 王永, 等. 分数阶系统时域子空间辨识[J]. 信息与控制, 2011, 40(5): 658-667. Liao Z, Peng C, Wang Y, et al. Time domain subspace method for fractional order system identification[J]. Information and Control, 2011, 40(5): 658-667. |
| [4] | Hu S, Chen Y Q, Qiu T S. Fractional processes and fractional-order signal processing[M]. Berlin, Germany: Springer, 2012. |
| [5] | Das S, Saha S, Das S. On the selection of tuning methodology of FOPID controllers for the control of higher order processes[J]. ISA Transactions, 2011, 50(3): 376-388. |
| [6] | Luo Y, Chen Y Q, Wang C Y. Tuning fractional order proportional integral controllers for fractional order systems[J]. Journal of Process Control, 2010, 20(7): 823-831. |
| [7] | Podlubny I. Fractional-order systems and PIλDμ-controllers[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 208-218. |
| [8] | Monje C A, Vinagre B M, Feliu V. Tuning and auto-tuning of fractional order controllers for industry applications[J]. Control Engineering Practice, 2008, 16(7): 798-812. |
| [9] | Luo Y, Chen Y Q. Fractional order [proportional derivative] controller for a class of fractional order systems[J]. Automatica, 2009, 45(10): 2446-2450. |
| [10] | Vahid B, Mohammad S T. On tuning fractional order [proportional-derivative] controllers for a class of fractional order systems[J]. Automatica, 2013, 49(5): 2297-2301. |
| [11] | Valério D, Costa J S. Tuning of fractional PID controllers with Ziegler-Nichols-type rules[J]. Signal Processing, 2006, 86(10): 2771-2784. |
| [12] | Luo Y, Chen Y Q, Pi Y. Experimental study of fractional order proportional derivative controller synthesis for fractional order systems[J]. Mechatronics, 2011, 21(1): 204-214. |
| [13] | Wang D J, Gao X L. H∞ design with fractional-order PDμ controllers[J]. Automatica, 2012, 48(5): 974-977. |
| [14] | Zhao C N, Xue D Y, Chen Y Q. A fractional order PID tuning algorithm for a class of fractional order plants[C]//Proceedings of the IEEE International Conference on Mechatronics & Automation. Piscataway, NJ, USA, IEEE, 2005: 216-221. |
| [15] | Tenoutit M, Maamri N, Trigeassou J C. An output feedback approach to the design of robust fractional PI and PID controllers[C]//Proceedings of the 18th World Congress of the International Federation of Automatic Control. Laxenburg, Australia: IFAC Secretariat, 2011: 12568-12574. |
| [16] | Castillo F J, Feliu V, Rivas R. Design of a class of fractional controllers from frequency specifications with guaranteed time domain behavior[J]. Computers & Mathematics with Applications, 2010, 59(5): 1656-1666. |
| [17] | Vu T N L, Lee M. Analytical design of fractional-order proportional-integral controllers for time-delay processes[J]. ISA Transactions, 2013, 52(5): 583-591. |
| [18] | Li H S, Luo Y, Chen Y Q. A fractional order proportional and derivative (FOPD) motion controller: Tuning rule and experiments[J]. IEEE Transactions on Control Systems Technology, 2010, 18(2): 516-520. |



