1 引言
多传感器管理[1]是指通过对传感器系统中有限的传感器的工作方式及参数进行选择和设定,以获得整个系统某种具体度量特性(如检测概率、 跟踪精度、 识别概率等)的最优值. 在地面防空武器系统中,通过多传感器调度可以动态地协调传感器使用以实现系统整体跟踪性能的最大化,从而实现高精度跟踪目标.
目前解决多传感器管理的方法主要有: (1) 基于协方差控制的方法. 文[2, 3]分别讨论了基于协方差控制的集中式与分布式多传感器分配问题; 王琳[4]、 崔博鑫[5]利用协方差控制思想讨论了基于任务需求的传感器分配方案; 吴巍[6, 7, 8]基于协方差的方法对主被动传感器协同跟踪中的传感器分配方案进行了讨论. (2) 基于信息论的方法. 主要是利用Shannon信息增量[9, 10, 11]、 交叉熵[12]、 Kullback-Leibler分辨力增益[13]、 Rényi信息增量[14, 15, 16]等不同的方式描述量测前后信息的增量,从而实时调整传感器资源,实现不同任务下传感器资源的有效利用. (3) 基于规划论和智能优化算法的方法. 该方法侧重于模型的建立及模型的求解,杨海燕[17]提出了一种适用于分布式跟踪的动态传感器管理方法,并用蚁群算法实时求近似优解; 杨啸天[18]在考虑传感器协同能力基础上建立了传感器管理模型,并提出了一种遗传—粒子群混合优化策略; 文[19, 20]利用粒子群算法对传感器分配问题进行了讨论.
与Shannon信息增量、 K-L分辨力增益等相比,Rényi信息增量更加强调某个局部信息,从而更具有灵活性和普适性[14]. 鉴于此,本文针对地面防空武器系统,面向机动目标跟踪任务,提出了基于Rényi信息增量的多传感器管理方案.
2 交互式多模型容积卡尔曼滤波算法2.1 容积卡尔曼滤波
对于非线性系统的状态估计问题,常用的滤波算法有扩展卡尔曼滤波(EKF)、 不敏卡尔曼滤波(UKF)、 粒子滤波(PF)及容积卡尔曼滤波(CKF). CKF是基于曲面径向准则的滤波算法,采用一组等权值的Cubature点集解决贝叶斯滤波积分问题. 与其它高斯非线性滤波算法相比,具有更优的非线性逼近能力(2阶矩)、 数值精度以及滤波稳定性[21, 22].
考虑非线性动态系统:
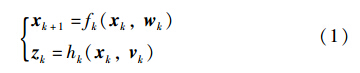
其中,xk∈Rn,zk∈Rm为k时刻系统状态向量和量测向量; fk(·)、 hk(·)为系统状态演化映射和量测映射; wk、 vk分别是协方差阵为Qk、 Rk的n维过程演化噪声和m维量测噪声. CKF算法如下:
选取m=2n个Cubature点ξi(其权值为ωi):
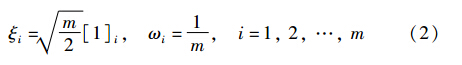
若、 Pt分别表示t时刻状态向量估计值及估计协方差,则容积点(i=1,2,…,m)的计算方式如下:

Pt=StSTt.
(1) 状态预测:
① 计算预测状态容积点(Xi,k-1k-1为容积点):
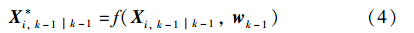
② 估计预测状态与预测协方差:
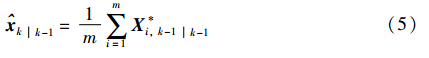
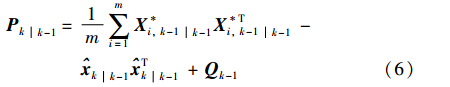
(2) 量测更新:
① 计算预测量测容积点(Xi,kk-1为容积点):
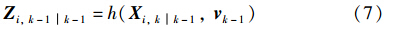
② 估计预测量测值、 新息协方差、 互协方差:

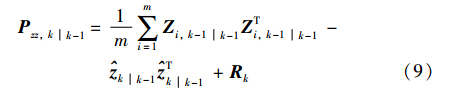

③ 状态更新:
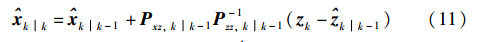
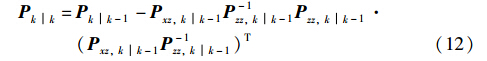
2.2 交互式多模型容积卡尔曼滤波算法
交互式多模型(IMM)算法是一种关于混合系统状态估计的次优算法[23],能够很好地满足实际中对机动目标跟踪的需求. 本文将该模型与CKF相结合,形成交互式多模型容积卡尔曼滤波(IMM-CKF)算法,用以解决高斯非线性系统状态估计问题.
IMM-CKF包括一个交互作用器、 多个CKF滤波器、 一个模型概率估计器和一个估计混合器. 交互作用器为IMM-CKF的输入端,由上一时刻各滤波器的估计初始化这一时刻的模型条件; 模型概率估计器用于获得各模型的概率; 各CKF滤波器并行工作,获得系统的状态估计; 最后估计混合器输出交互计算结果.
(1) 输入交互:
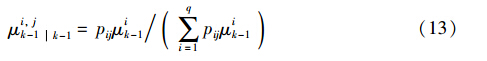
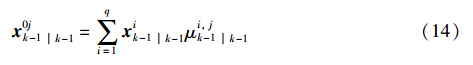
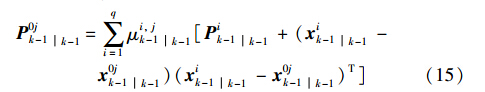
其中,pij表示马尔可夫链中模型j转移到模型i的概率,μi,jk-1k-1表示k-1时刻模型i的条件概率,μik-1表示k-1时刻模型i的概率,x0jk-1k-1、 P0jk-1k-1分别表示模型j的重初始化状态估计及协方差,xik-1k-1、 Pik-1k-1分别表示模型i在k-1时刻的估计及协方差.
(2) 各模型CKF滤波器平行滤波,得到各模型k时刻的估计xjkk、 Pjkk,并通过量测预测值zkk-1、 量测预测残差Sjk得到各模型的似然度:
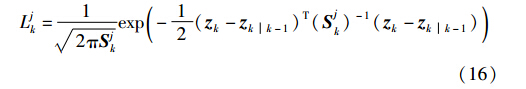
(3) 模型概率更新:

(4) 估计融合:
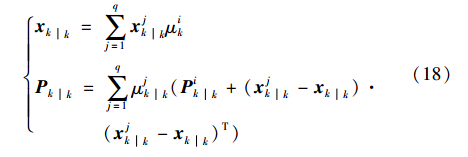
3 Rényi信息增量
多传感器管理的目的就是通过实时调整传感器的使用,探测更全面、 更可靠的目标相关信息,减少目标环境的不确定性,这种不确定性可以用信息论中的熵、 互熵、 分辨力增益、 信息增量等方式来度量. Shannon熵常用以描述一个事件的信息. 假设先、 后验概率密度函数p0、 p1分别服从高斯分布p0~Gμ0,Σ0,p1~Gμ1,Σ1 ,基于Shannon熵的信息增量[9]为

Rényi熵是Shannon熵的广义形式,反映了系统信息的高阶特性. 随机变量X由概率f1变化为f2,其Rényi信息增量被定义为
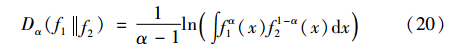
参数α的设置使Rényi信息增量对信息的度量更具有一般性和灵活性. 不同的取值强调概率分布的不同部分,例如,当α=1时,Rényi信息增量即为K-L分辨力函数. 文[17, 18]详细分析了参数α的变化对Rényi信息增量的影响,其结果表明当α=0.5时强调分布函数的尾部,可以对两个相似的概率分布是否达到最佳进行辨别. 因此在跟踪时选取α=0.5可获得较好的跟踪性能[14, 24, 25].
针对目标跟踪而言,不同的传感器对同一目标进行跟踪,由于其跟踪性能不同使得在一次量测后目标的后验概率密度函数不同,因此可以基于先、 后验概率密度函数的Rényi信息增量对传感器进行动态管理. Rényi信息增量为

4 面向机动目标跟踪的多传感器管理
4.1 基于Rényi信息增量的多传感器管理模型
针对地面防空武器,面向机动目标跟踪的任务提出了基于Rényi信息增量的多传感器管理模型. 该模型利用IMM-CKF算法解决高斯非线性环境下系统状态估计问题,利用滤波结果计算各目标和各传感器配对时的Rényi信息增量,以传感器系统总效能最大为原则选择传感器进行目标跟踪,建立基于Rényi信息增量的多传感器管理模型. 其优势在于以下两个方面:
① IMM-CKF滤波算法具有较优的非线性逼近能力、 数值精度及滤波稳定性,有效提高了非线性运动模型中目标状态估计的准确性. 一方面从滤波结果上提高目标的跟踪精度; 另一方面,精确的状态估计是传感器管理的前提,有助于实现传感器资源的有效利用,从而提高目标跟踪精度,并为下一时刻的估计提供准确的输入数据.
② 由式(19)、(21)对比可以看出,基于Shannon熵的信息增量仅包含了概率密度函数的一个特征值,而Rényi信息增量比较的是概率密度函数的近似程度,更能够表征信息的差异,为目标跟踪时传感器一次量测前后信息的增量提供更加精确的度量.
假设某地面防空武器系统来袭目标m个,我方共有探测传感器n部. 基于Rényi信息增量的多传感器管理模型可描述为在一定约束条件下,寻求目标—传感器配对矩阵X,使得多传感器系统的总效能Ep最大,即:
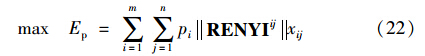
约束条件:
① 传感器最大跟踪能力约束:
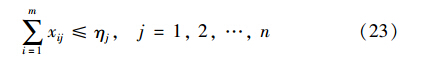
② 目标数目约束:

③ 目标被执行跟踪容量约束:

式中,RENYIij为传感器j跟踪目标i的Rényi信息增量,由式(19)计算可得; xij为传感器配对矩阵X中的元素,若传感器j跟踪目标i,则xij=1,否则,xij=0; pi为目标i的优先级,主要根据上级是否指定、 是否有攻击意图、 攻击何种目标、 目标机型等因素综合判断; ηj为传感器j的最大跟踪能力.
4.2 算法实现步骤
建立基于Rényi信息增量的多传感器管理模型,以系统总效能最大为原则选择传感器进行目标跟踪,最终实现传感器资源的有效利用,基本步骤如图 1所示.
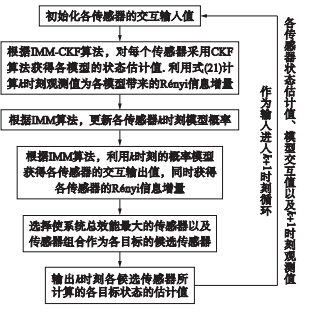 |
| 图 1 基于Rényi信息增量的多传感器管理步骤流程图Fig. 1 The flow diagram of the multi-sensor management based on Rényi information gain |
5 算例仿真
仿真场景描述: 地面防空武器系统检测到来袭目标3个(m=3),记为T1、 T2、 T3,其运动模型均为非线性高斯模型,目标优先级函数P=[0.5 0.8 0.9]. 现多传感器跟踪系统共有3部跟踪传感器(n=3),为只具有单目标跟踪能力的雷达,记为S1、 S2、 S3.
表 1为各雷达量测噪声. 仿真实验中各雷达同步采样,采样周期为1 s,采样时间为100 s,Monte Carlo仿真次数为100.
| 传感器 | x标准差 | y标准差 | 相关系数 | |
| S1 | 12.7 | 13.2 | 0.82 | |
| S2 | 10.1 | 9.6 | -0.74 | |
| S3 | 8.4 | 9.3 | 0.42 |
采用不确定性椭球描述3部雷达的精度,定义为: 对于任意给定的n维对称正定方阵W>0,与之相对应的不确定性椭球为

椭球面积越小,该雷达量测精度越高. 绘制各雷达量测精度的不确定性椭球如图 2所示. 根据椭球面积对各雷达的量测精度进行排序,由高到底依次为S3、 S2、 S1.
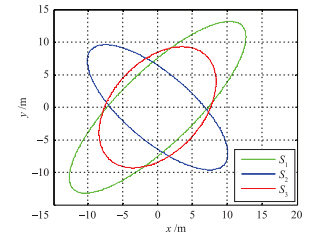 |
| 图 2 雷达量测精度的不确定性椭球Fig. 2 Uncertain ellipses of radars′ measurement accuracy |
设定如下3种跟踪方案:
方案1: 固定方案. 根据目标优先级以及传感器量测精度关系,由量测精度高的S3跟踪优先级高的T3,S2跟踪T2,S1跟踪T1.
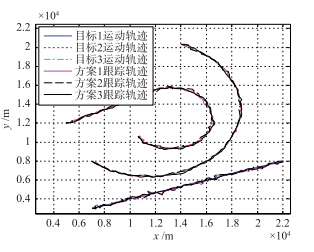 |
| 图 3 真实航迹以及各跟踪方案跟踪结果Fig. 3 The true track and the tracking result of each scheme |
方案2: 基于Shannon信息增量的多传感器多目标跟踪方案.
方案3: 基于Rényi信息增量的多传感器多目标跟踪方案.
图 3和图 4是各方案跟踪结果和跟踪性能对比. 表 2为100次Monte Carlo仿真的均方根误差均值.
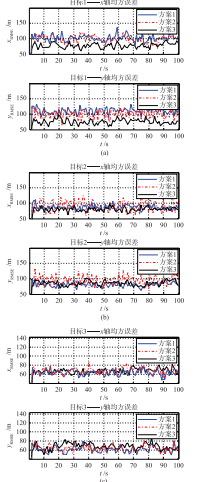 |
| 图 4 3种方案跟踪性能比较Fig. 4 Comparison among three tracking schemes |
| 均方根误差(RMSE) | |||
| 方案1 | 方案2 | 方案3 | |
| 目标1 | |||
| X轴 | 101.034 1 | 96.495 9 | 74.505 2 |
| Y轴 | 110.534 1 | 100.435 5 | 76.555 1 |
| 目标2 | |||
| X轴 | 80.490 6 | 86.702 0 | 72.989 4 |
| Y轴 | 75.880 8 | 86.826 4 | 74.890 5 |
| 目标3 | |||
| X轴 | 63.834 8 | 66.619 9 | 68.563 5 |
| Y轴 | 62.434 2 | 67.657 5 | 68.054 6 |
对3种跟踪方案进行对比,方案1采用固定跟踪方案,高跟踪精度传感器跟踪高优先级目标,目标3虽然取得了很好的跟踪效果,但这是以牺牲目标1和目标2的跟踪效果为代价的,尤其目标2虽然与目标3优先级相近,但跟踪精度却低很多,这种方案实际上显然是不可取的. 方案2以跟踪过程中多传感器系统的Shannon信息增量最大化为原则对多传感器进行管理,目标3的跟踪效果虽然不如方案1,但是一定程度上权衡了3个目标的跟踪效果. 方案3以跟踪过程中多传感器系统的Rényi信息增量最大化为原则对多传感器进行管理时,对3个目标的跟踪精度进行了更佳的权衡,目标3的跟踪精度与方案1和2相差无几,同时较大地提高了目标1和2的跟踪精度. 这是由于Rényi信息增量比较的是概率密度函数的近似程度,而Shannon信息增量比较的仅是概率密度函数的一个特征值,因此Rényi信息增量更能够表征信息的差异,可见基于Rényi信息增量的传感器管理方案实现了传感器资源的合理利用,相比与方案1和方案2能够有效地提高整个跟踪系统的跟踪效果.
6 结束语本文针对地面防空武器系统中的机动目标跟踪问题,提出了一种基于Rényi信息增量的多传感器管理方案. 结合IMM算法和CKF较好地处理了非线性高斯模型中目标状态滤波估计问题,实现了对机动目标运动状态的准确估计,以计算传感器—目标配对Rényi信息增量. 建立了基于Rényi信息增量的多传感器管理模型,并进行了关联仿真. 仿真对3种跟踪方案进行了对比,表明基于Rényi信息增量的多传感器管理模型能够实现传感器资源的合理利用,提高多传感器系统的整体性能. 针对传感器调度问题,当传感器和目标数目相对较多时,难以保证模型求解的时效性,因此,探索适用于传感器调度模型的优化算法是下一步有待研究的问题.
| [1] | 罗开平, 姜维, 李一军. 传感器管理述评[J]. 电子学报, 2010, 38(8): 1900-1907. Luo K P, Jiang W, Li Y J. Review of sensor management[J]. Acta Electronics Sinica, 2010, 38(8): 1900-1907.. |
| [2] | 周文辉, 胡卫东, 余安喜. 基于协方差控制的集中式传感器分配算法研究[J]. 电子学报, 2003, 31(12): 2158-2162. Zhou W H, Hu W D, Yu A X. A study of sensor allocation algorithm based on covariance control in centralized multisensory systems[J]. Acta Electronics Sinica, 2003, 31(12): 2158-2162.. |
| [3] | 韩海峰, 周文辉, 陈国海. 目标跟踪中协方差控制的分布式多传感器管理[J]. 现代雷达, 2007, 29(1): 47-50. Han H F, Zhou W H, Chen G H. Decentralized multi-sensor management algorithm based on covariance control for target tracking[J]. Modern Radar, 2007, 29(1): 47-50.. |
| [4] | 王琳, 于雷, 寇英信. 以任务需求为驱动的多传感器资源管理方法[J]. 系统工程与电子技术, 2010, 32(9): 1925-1930. Wang L, Yu L, Kou Y X. Multi-sensor resource management method driven by task requirement[J]. Systems Engineering and Electronics, 2010, 32(9): 1925-1930. . |
| [5] | 崔博鑫, 许蕴山, 夏海宝, 等. 基于任务控制的动态多传感器管理方案[J]. 系统工程与电子技术, 2012, 34(12): 2473-2478. Cui B X, Xu Y S, Xia H B. Dynamic multi-sensor management algorithm based on task control[J]. Systems Engineering and Electronics, 2012, 34(12): 2473-2478.. |
| [6] | 吴巍, 王国宏, 柳毅. 机载雷达、红外、电子支援措施协同跟踪与管理[J]. 系统工程与电子技术, 2011, 33(7): 1517-1522. Wu W, Wang G H, Liu Y. Airborne radar/IRST/ESM synergistic tracking and management[J]. S ystems Engineering and Electronics, 2011, 33(7): 1517-1522. . |
| [7] | 吴巍, 王国宏, 双炜. 多机载平台多目标跟踪与辐射控制[J]. 系统工程与电子技术, 2012, 34(3): 495-501. Wu W, Wang G H, Shuang W. Multi-airborne-platform multi-target tracking and radiation control technology[J]. . Systems Engineering and Electronics, 2012, 34(3): 465-501. |
| [8] | 吴巍, 王国宏, 李世忠. 给定辐射时间限制下的雷达辐射时机最优规划研究[J]. 兵工学报, 2012, 33(4): 41-47. Wu W, Wang G H, Li S Z. Research on optimum scheduling for radar radiation occasions with emission time constraint[J]. Acta Armamentarii, 2012, 33(4): 41-47. . |
| [9] | 李彬彬, 冯新喜, 王朝英, 等. 基于信息增量的多被动传感器资源分配算法[J]. 系统工程与电子技术, 2012, 34(3): 502-507. Li B B, Feng X X, Wang C Y, et al. Multi-passive sensors resource allocation algorithm based on information gain[J]. Systems Engineering and Electronics, 2012, 34(3): 502-507. . |
| [10] | Ji Q, Zhang Y. Efficient sensor selection for active information fusion[J]. IEEE Transactions on Systems, Man, and Cybemetics, 2010, 40(3): 719-728. |
| [11] | 刘先省, 赵巍, 潘泉. 用于检测与分类的多传感器管理算法研究[J]. 西北工业大学学报, 2001, 19(1): 27-30. Liu X S, Zhao W, Pan Q. An algorithm of multisensor management used in detection and classification[J]. Journal Northwestern Polytechnical University, 2001, 19(1): 27-30. . |
| [12] | 卢迪, 赵洪, 张开玉. IMMKF中基于交叉熵的传感器管理算法[J]. 系统仿真学报, 2011, 23(7): 1426-1433. Lu D, Zhao H, Zhang K Y. Multi-sensor management based on cross-entropy in IMMKF[J]. Journal of System Simulation, 2011, 23(7): 1426-1433.. |
| [13] | 刘先省, 周林, 杜晓玉. 基于RIMMKF的一种传感器管理算法[J]. 电子学报, 2007, 35(12): 2247-2251. Liu X X, Zhou L, Du X Y. An algorithm of sensor management based on RIMMKF[J]. Acta electronica Sinica, 2007, 35(12): 2247-2251.. |
| [14] | 刘钦, 刘峥. 一种基于Renyi信息增量的机动目标协同跟踪方法[J]. 控制与决策, 2012, 27(9): 1437-1440. Liu Q, Liu Z. A method of maneuvering target collaboration tracking based on Renyi information gain[J]. Control and Decision, 2012, 27(9): 1437-1440. . |
| [15] | Aughenbaugh J M, LaCour B R. Sensor management for particle filter tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 503-523. |
| [16] | Kreucher C M, Kastella K D, Hero A O, et al. Information-based sensor management for multi-target tracking[C]//Proceeding of SPIE on Signal and Data of Small Traget. 2003: 480-489. |
| [17] | 杨海燕, 尤政, 王琳. 协同网络下分布式跟踪的动态传感器管理[J]. 华南理工大学学报, 2012, 35(5): 1000-1007. Yang H Y, You Z, Wang L. Dynamic sensor management for distributed tracking in collaborative network[J]. Journal of South China University of Technology, 2012, 35(5): 1000-1007.. |
| [18] | 杨啸天, 冯金富, 冯媛. 基于遗传粒子群的多传感器目标分配算法[J]. 电光与控制, 2011, 18(3): 5-8. Yang X T, Feng J F, Feng Y. A multi-sensor target assignment based on genetic particle swarm optimization[J]. Electronics Optics and Control, 2011, 18(3): 5-8.. |
| [19] | 王博, 盛卫东, 安玮. 基于粒子群优化的传感器管理算法研究[J]. 信号处理, 2009, 25(7): 1135-1140. Wang B, Sheng W D, An W. Research on PSO based sensor management algorithms[J]. Signal Processing, 2009, 25(7): 1135-1140. . |
| [20] | 王一川, 单甘霖, 童俊. 基于协同memticPSO算法的传感器—目标分配问题求解[J]. 系统工程与电子技术, 2013, 35(5): 1000-1007. Wang Y C, Shan G L, Tong J. Solving sensor-target assignment problems based an cooperative memticPSO algorithm[J]. Systems Engineering and Electronics, 2013, 35(5): 1000-1007.. |
| [21] | 孙妍, 鲁涤强, 陈启军. 一种基于强跟踪的改进容积卡尔曼滤波器[J]. 华中科技大学学报, 2013, 41(增刊I): 451-454. Sun Y, Lu D Q, Chen Q J. An improved cubature Kalman filters based on strong tracking[J]. Journal of Huazhong University of Science and Technology, 2013, 41(Sup. I): 451-454. . |
| [22] | 鹿传国, 冯新喜, 张迪. 基于改进容积卡尔曼滤波的纯方位目标跟踪[J]. 系统工程与电子技术, 2012, 34(1): 27-33. Lu C G, Feng X X, Zhang D. Pure bearing tracking based on improved cubature Kalman filter[J]. Systems Engineering and Electronics, 2012, 34(1): 27-33. . |
| [23] | 韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M]. 2版. 北京: 清华大学出版社, 2010: 60-62. Han C Z, Zhu H Y, Duan Z S. Multi-source information fusion[M]. 2nd ed. Beijing: Tsinghua University Press, 2010: 60-62. |
| [24] | Kreucher C M, Kastella K D, Hero A O, et al. An information-based approach to sensor management in large dynamic networks[J]. Proceedings of the IEEE, 2007, 95(5): 978-999. |
| [25] | Liu Y, Wang H. UKF based nonlinear filtering using minimum entropy criterion[J]. IEEE Transactions on Signal Processing Journal of Astronautics, 2013, 61(20): 4988-4999. |



