2. 盐城工学院信息工程学院, 江苏 盐城 224051
2. School of Information Engineering, Yancheng Institute of Technology, Yancheng 224051, China
1 引言
社区结构(community structure)是继小世界效应和无标度特征之后发现的又一个重要网络拓扑结构特性[1, 2],目前社区尚无严格的数学定义,但社区通常被认为是网络中的节点内聚子图,子图内部的节点间连接紧密,而子图间的连接较为疏松[3]. 社区结构表示真实网络可以看作是由许多不同类型节点组合形成的,如在生物网络中的功能子团、 人际关系网中的朋友圈子、 科学家协作网中的科研团队等.
社区检测(community detection)早已成为复杂网络领域中的一个重要研究分支. 大部分已有研究工作聚焦于静态网络的社区检测,静态网络既可以表示一段时间上的数据聚合,也可以表示一个时间点上的快照[4],从早期的以最小化割的图分割方法(如Kernighan-Lin算法[5]),到著名的以优化模块性(modularity)的Fast Newman方法[6],都属于静态网络社区检测的范畴.
2006年,Kossinets和Watts在《Science》上发表的论文指出[7],实际社会网络随时间而演变,时间是社会网络分析应该考虑的重要因素. 社区结构易随时间演化更是显而易见,如政治社区在选举前后的活跃程度可能差别很大,某社区中的个体也有可能转移兴趣或受到特定事件影响而迁移到另一社区[8]. 动态网络通常建模为连续时间点上的快照(snapshot)序列,动态网络上社区演化分析可以看作是静态网络上社区检测的泛化. 社区演化分析试图揭示动态网络社区结构随时间的演变过程,除了与静态网络上社区检测一样考虑快照的拓扑结构之外,社区演化分析还需融入前一时刻社区结构对当前时刻的影响作用.
动态网络社区演化分析试图融合当前时刻快照拓扑结构和上一时刻社区结构两个因素,挖掘当前时刻的社区结构. 本文首先构建刻画当前时刻社区结构优劣的目标函数,将社区演化分析形式化为优化问题; 然后,利用随机分块模型(stochastic block model,SBM)描述当前时刻快照拓扑结构与社区结构之间的关系及Dirichlet分布构建上一时刻社区结构与当前时刻社区结构之间的关联,从而推导出目标函数的可计算形式. 在Chi等人提出的谱聚类框架下[9],本文证明了社区演化分析目标函数与谱聚类目标函数是等价的,架设起利用谱聚类解决动态社区演化分析问题的桥梁,从而提出基于谱聚类的社区演化分析算法.
2 相关工作静态网络上的社区检测问题长期受到关注,国内外研究者提出数以千计的方法来应对这一问题[1, 2, 3, 10],这些方法总体可以分为2类: 有全局目标函数和无全局目标函数. 有全局目标函数的方法将社区检测问题归为该目标函数上的最优化问题,由于目标函数最优化是NP(non-deterministic polynomial)难问题,为此,研究者围绕目标函数定义和启发式策略展开了广泛研究[2, 6, 11]. 无全局目标函数的方法从刻画节点间连接紧密程度出发,将紧密连接的节点凝聚成局部结构,再将所有局部结构组装成全局的社区结构,如Palla等人提出的邻接k团合并方法[12].
近年来,动态网络上的社区演化问题受到越来越多的关注,社区演化分析本质上属于演化数据学习[13],希望观察社区的出现、 变化、 分裂和消失这一动态过程. 社区演化分析亦可分为2类[8]: (1) 采用2阶段方法,先把每个快照视为一个静态网络,进行社区检测,再分析快照上社区随时间的演化. (2) 采用统一框架,将社区检测和演化融合到一起. 由于两阶段方法未能考虑前后时刻社区结构之间的联系,因此社区检测和演化的统一框架逐渐引起研究者的广泛重视. Tantipathananandh等人的解决方案则有所不同,他们将社区演化建模为图着色问题[14],并考虑到网络中存在一些不属于任何社区的点,从而得到大部分点的社区演化序列[15]. Tang等人则致力于解决异构社会网络中的社区演化问题[16]. 大部分方法利用随机分块模型将社区演化分析建模为优化问题,然后基于已有方法,如Gibbs抽样[8]和演化聚类[4]等,提出启发式算法来解决. 本文的研究延续利用优化方法解决社区演化分析这一思路,与现有工作的主要区别在于: 将上一时刻社区结构的影响作用直接融入目标函数,而非间接地根据上一时刻社区结构估计目标函数中的某些参数[8]. 本文从理论上证明了社区演化分析目标函数与谱聚类目标函数是等价的,为利用谱聚类解决社区演化分析优化问题奠定了基石.
3 问题定义静态网络关系通常用图来描述:G(V,E),其顶点集是V; 边集是E,可以使用一个n×n的邻接矩阵W来描述,W中元素xij是二值的,1表示顶点i和顶点j之间有边连接,0表示没有. 随着时间的推移,社会网络关系发生变化,如果将一段时间划分成T个离散时间点,整个网络被建模为T个离散时间点上的快照WT=[W(1),W(2),…,W(T)][8]. 社区演化问题试图获得T个离散时间点上的社区结构演化序列ZT={Z(1),Z(2),…,Z(T)},Z(t)是一个矩阵,其元素表示在t时刻顶点i被划分到第k个社区. 显然,t时刻社区结构受到t-1时刻社区结构和t时刻网络关系共同的影响,因此有:
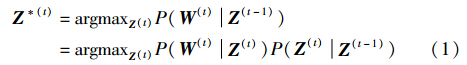
式(1)的优化函数可解释为在已知上一时刻社区结构条件Z(t-1)下,找到最好的当前社区结构Z(t),使得当前时刻网络结构W(t)发生的概率最大,式(1)最大化目标函数可以重写成式(2):
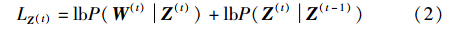
由式(2)可知,优化函数LZ(t)由2部分组成: P(W(t)Z(t))刻画了t时刻快照下网络和社区结构之间的关系,P(Z(t)Z(t-1))建立起两个连续时刻间社区结构之间的关系. 3.1节和3.2节分别讨论P(W(t)Z(t))和P(Z(t)Z(t-1))的建模过程,从而给出的整体建模.
3.1 基于随机分块模型的P(W(t)Z(t))建模由于P(W(t)Z(t))刻画了t时刻快照下网络拓扑和社区结构之间的关系,相当于在静态网络下的社区划分过程,随机分块模型是在静态网络社区划分中得到成功应用的经典模型,本文借助于随机分块模型对P(W(t)Z(t))进行建模. 设网络在t时刻由K个社区组成,将社区结构Z(t)视作n×K矩阵,元素zik表示顶点i属于社区k. 定义K×K的转移矩阵Λ(t),其元素λkl表示节点从第k个社区转移到第l个社区的概率,显然有∑lλkl=1. 据此,定义Φij(t):
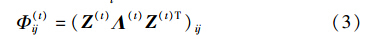
式(3)刻画出了n个网络顶点之间的相似关系,Φij(t)值越大,表明顶点i和j的相似度越高. 实际上,集合{Φij(t)}是一个二部图,一侧节点是n个网络顶点,另一侧节点是K个社区. 由此,本文将P(W(t)Z(t))建模为参数Φij(t)的多项式分布:
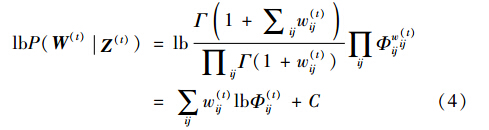
其中,Γ(·)是Gamma函数,C为常数. 常数C在优化问题中不予以考虑,至此完成了P(W(t)Z(t))的建模.
3.2 基于Dirichlet分布的P(Z(t)Z(t-1))建模由于Z(t)Λ(t)能唯一决定Z(t)和Λ(t),因此有P(Z(t)Z(t-1))=P(Z(t)Λ(t)Z(t-1)Λ(t-1)),即P(Z(t)Z(t-1))是P(W(t)Z(t))的共轭分布. 3.1节将P(W(t)Z(t))建模为多项式分布,得出P(Z(t)Z(t-1))满足Dirichlet分布. 因此,本文假设Z(t)Λ(t)满足参数为ψ(t)的Dirichlet分布,得到式(5):
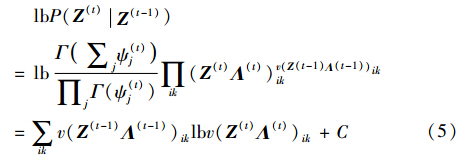
其中,ψ(t)为Dirichlet分布的参数,有ψ(t)=v·vec(Z(t-1)·Λ(t-1))+1,vec(·)表示矩阵的向量化,v表示当前时刻Dirichlet分布参数向量与上一时刻顶点迁移向量之间的常数倍关系. 根据式(4)、 (5)容易得到式(2)的优化函数LZ(t)的最终形式,如下所示:
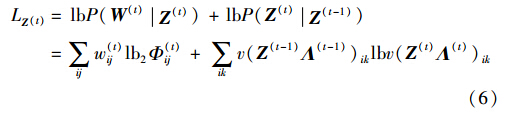
实际上,优化函数LZ(t)的两部分分别由随机分块模型及其共轭分布所遵循的Dirichlet分布导出,即同一时间点上社区分布和网络拓扑结构上的条件概率可以用随机分块模型建模,而某个时间点与其上一个时间点上社区分布遵循Dirichlet分布. 给出式(6)的社区演化目标函数后,需要设计优化算法求解.
4 基于演化谱聚类的解决方案数据的分布随时间的变化而逐渐变化,这类数据的学习问题被称为演化数据学习[11]. 显然,动态社会网络社区演化分析属于典型的演化数据学习. 演化数据学习中的一个重要问题就是聚类分析,它是发掘数据演化机制的重要手段,引起学者们的广泛关注. Chakrabarti等人在2006年首次明确定义了演化聚类问题[15],随后,Chi等人于2007年提出基于谱聚类(spectral clustering)的演化聚类框架[8]. 本文发现式(6)所示的优化函数LZ(t)与Chi等人提出的演化谱聚类密切关联,求解LZ(t)可以通过演化谱聚类框架来解决. 本节首先简要介绍演化谱聚类框架,然后,给出社区演化分析归化到演化谱聚类框架的过程.
4.1 演化谱聚类框架演化谱聚类框架的关键是定义衡量演化数据聚类质量的代价函数,Chi等人给出了代价函数定义的通用框架,代价函数由2部分组成: (1) 快照代价(SC),衡量在当前时间点数据特征分布下的聚类质量; (2) 时间代价(TC),衡量在历史时间点数据特征过渡到当前时间点特征的平滑性. 简言之,SC考虑了当前时间点上聚类质量的优劣,而TC考虑了历史数据的影响. 代价函数C定义如式(7)所示:

其中,α和β是规格化权重,即α+β=1,0≤α≤1. α和β反映出具体应用对快照代价和时间代价的偏重程度.
谱聚类将聚类问题转化为图分割(graph partitioning)问题[15],将样本看作顶点,样本间的相似度看作带权的边,目标是找到一种图分割的方法使得连接不同组的边的权重尽可能低,组内的边的权重尽可能高. 从图论角度看,谱聚类试图找到割(cut),通过割将图节点分成两部分,使得通过割的边(边的连接点分别在割的两侧)权重最小. 因此,规格化割(normalized cut,NC)成为谱聚类最常用的目标函数之一,令k为类簇数量,NC计算公式为
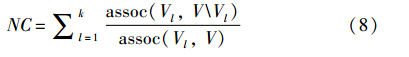
其中,Vl为第l个类簇,V\Vl为Vl的补集,assoc(V1,V2)为V1和V2顶点之间的边数量. 据此,谱聚类伪代码如算法1所示,首先构造图G的拉普拉斯矩阵L,然后,计算L的前K个特征值,从而将n×n维矩阵降到n×K维,最后在n×K维上用K均值算法获得K个类簇.
算法1 基于谱聚类的图分割算法
|
输入: 图G的n×n维邻接矩阵W,社区数量K. 输出: 1×n维标记向量π[n],其中π[i]表示第i个点所属社区 |
| (1) 构建稀疏矩阵D,Dii=deg[i]; /*deg[i]表示顶点i的度*/ (2) L=D-W; /*L为图G的拉普拉斯矩阵*/ (3) 计算L矩阵的前K个特征值,对应的n维特征向量为zk,k=1,…,K; (4) 由K个n维特征向量构建n×K维矩阵L′; (5) π[n]=Kmeans(L′,K);/*利用Kmeans算法将矩阵聚成K个类簇*/ (6) return π[n] |
Chi等人的工作架设起时变数据过渡到谱聚类的桥梁,通过推导出NC在式(7)所示代价函数下的形式,演化聚类可以通过谱聚类算法来解决. 本文仅给出NC代价函数CNC的公式,详细推证过程见文[9]:
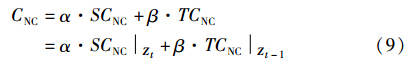
4.2 从社区演化分析到演化谱聚类
由4.1节的分析可知,如果能给出社区演化分析的代价函数,就能利用谱聚类算法来求解社区演化分析的目标函数. 而社区演化正是试图从当前时刻网络拓扑结构及历史时刻社区结构出发,寻求当前时刻最优的社区结构,这与式(7)给出的代价函数非常契合.
3.1节利用二部图{Φij(t)}对t时刻快照W(t)建模,因此,可定义Φ(t)ij与W(t)之间的距离为快照代价SC,含义为: Φ(t)ij与W(t)之间距离越大,SC越大,即在W(t)上的社区划分质量越差. 由于KL-divergence能很好地刻画高维稀疏向量之间的距离,本文选取KL-divergence[19]为距离计算公式,设x和y为两个向量,KL-divergence的计算公式为
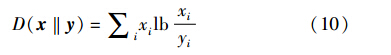
社区演化分析中快照代价SC定义为
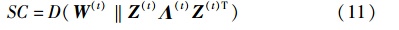
时间代价TC刻画了t-1时刻与t时刻之间社区结构的变化程度,同样可以用KL-divergence来衡量,于是,TC可以定义为
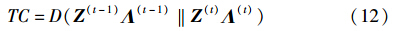
由此得到社区演化分析问题的代价函数CKL:
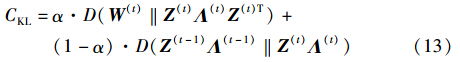
谱聚类试图最小化式(13)所示的CKL,而社区演化分析则试图最大化式(6)所示的LZ(t),下面定理证明了当v=(1-α)/α时,最小化CKL和最大化LZ(t)是等价的.
定理1 当v=(1-α)/α时,最小化式(13)所示的CKL等价于最大化式(6)所示的LZ(t).
证明 由于∑ij(W(t))ij为常数,不失一般性,设∑ij(W(t))ij=1,有:
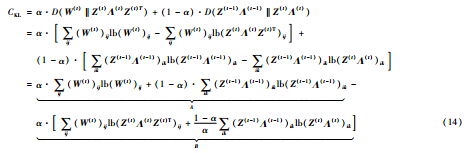
因为∑ij(W(t))ij=1,有∑kλ(t)k=1,因此式(14)的A部分为常数. 由此,最小化CKL等价于最大化式(14)的B部分,由式(6)可知,令v=(1-α)/α,B部分即为式(6),得证.
综上所述,利用KL-divergence定义了社区演化问题在演化谱聚类框架下的代价函数,定理1证明了演化谱聚类最小化该代价函数与前面推导的最大化LZ(t)是等价的,这架设起了社区演化问题过渡到演化谱聚类框架的桥梁,基于算法1所示的谱聚类算法,容易得出社区演化的优化算法.
5 实验评价5.1 实验设置
由于合成网络具有真实标记(ground truth),适用于精确地评估算法性能,本文利用Newman和Girvan[20]公布的合成网络为实验数据集,该网络包含128个节点,被平均划分到4个社区,即每个社区包含32个节点. 本文产生50个时间点的网络快照: 在每个社区随机抽取一定比例的节点,随机选择另外3个社区进行迁移,然后,按照网络pin随机添加与同个社区内节点之间的边,按照网络pout随机添加与不同社区节点之间的边. 实验在两种场景下进行: (1) pin=0.05,pout=0.16,表示社区结构较为清晰的网络; (2) pin=0.06,pout=0.12,表示社区结构较为模糊的网络. 接着,实验设置两种不同的迁移节点比例(TP)为10%和30%,表明从t-1时刻到t时刻发生迁移节点的数量.
由于传统谱聚类都以规格化割NC为优化目标[16],因此,本文实验以基于NC优化的谱聚类为比较对象,称为NC_Spec. 本文提出的方法本质上以KL-divergence距离为优化目标,因此称为KL_Spec. 由于实验数据集具有ground truth信息,因此,本文以错误率为评价指标,社区标记Z可以表示成128×4的矩阵,每行对应一个节点,每列对应一个社区,zik=1表示第i个节点属于第k个社区. 同理,ground truth信息亦可表示为128×4的矩阵G,本文用范数计算错误率,如式(15)所示:
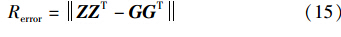
5.2 实验结果
首先,本文将KL_Spec中参数α设为0.8,即v=1/4. 图 1给出随时间变化,KL_Spec和NC_Spec两种算法在错误率指标上的性能比较结果. 可以看出,在几乎所有的时间点上,KL_Spec都具有较低的错误率. 表 1给出图 1中所有时刻错误率的均值和方差两种统计信息,KL_Spec比NC_Spec均值和方差小,这表明KL_Spec得到的社区质量较高,而且随时间变化具有更好的稳定性. 当节点迁移比例从10%提升至30%时,由于更多的节点呈现出动态性,两种算法的错误率都相应增加,但是,KL_Spec错误率均值和方差的增幅小于NC_Spec增幅,这说明KL_Spec对网络动态性的适应性较强.
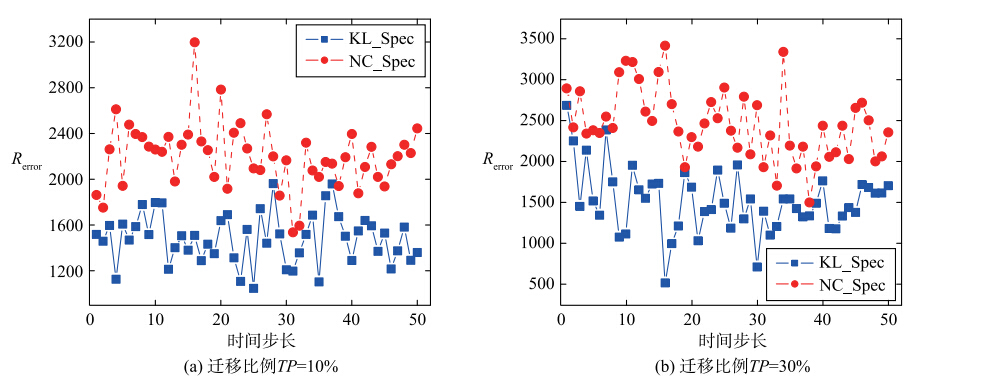 |
| 图 1 KL_Spec和NC_Spec性能比较Fig. 1 Performance comparison between KL_Spec and NC_Spec |
| KL_Spec/10% | NC_Spec/10% | KL_Spec/30% | NC_Spec/30% | |
| 均值 | 1484.5 | 2200.6 | 1516.5 | 2467.4 |
| 方差 | 218.3 | 285.5 | 393.0 | 427.9 |
其次,本文观察快照代价权重α对KL_Spec算法性能的影响,α在0.5~0.9之间以步长0.1递增,分别计算KL_Spec算法在TP=10%和TP=30%两种情况下错误率均值,得到如图 2所示的实验结果. 可以看出,错误率随α的增加而减小,这说明当前时刻下网络拓扑结构远比历史时刻带来的变化重要,即社区演化分析应首要考虑当前网络快照的拓扑结构,再结合考虑历史数据的影响. 同时发现,当α=0.8时,KL_Spec算法错误率基本降至最低,尽管当TP=30%时,α=0.9略优于α=0.8,这也是本文之所以选择α=0.8作为KL_Spec默认参数的缘由.
 |
| 图 2 α对KL_Spec算法性能的影响Fig. 2 Impact of α on the performance of KL_Spec algorithm< |
6 结论
本文研究动态网络中的社区演化分析问题,模型融合 当前时刻快照拓扑结构和上一时刻社区结构两个因素,并用随机分块模型和Dirichlet分布分别对上述两个因素建模,从而证明了社区演化分析与谱聚类是等价的. 以KL-divergence距离为优化目标,提出一种新颖的社区演化分析算法KL_Spec. 与传统的以规格化割为目标函数的谱聚类方法相比,实验结果表明所提方法在动态社区发现上具有更佳的准确率和稳定性.
在进一步的研究中,将本文方法扩展到大规模异构网络的社区演化分析,并在更多的实际数据集上进行广泛实验验证.
| [1] | 张忠元. 基于字典学习的网络社团结构探测算法[J]. 中国科学下辑: 信息科学, 2011, 41(11): 1343-1355. Zhang Z Y. Community structure detection in social networks based on dictionary learning[J]. Science in China Series F: Information Sciences, 2011, 41(11): 1343-1355... |
| [2] | 淦文燕, 赫南, 李德毅, 等. 一种基于拓扑势的网络社区发现方法[J]. 软件学报, 2009, 20(8): 2241-2254. Can W Y, He N, Li D Y, et al. Community discovery method in network based on topological potential[J]. Journal of Software, 2009, 20(8): 2241-2254.. |
| [3] | 冯霞, 陈卉敏, 李勇. 一种结合SVD的SNMF复杂网络社区发现方法[J]. 信息与控制, 2013, 42(3): 387-391. Feng X, Chen H M, Li Y. A complex network community discovery method of symmetric nonnegative matrix factorization combined with SVD[J]. Information and Control, 2013, 42(3): 387-391. . |
| [4] | Lin Y R, Chi Y, Zhu S, et al. Analyzing communities and their evolutions in dynamic social networks[J]. ACM Transactions on Knowledge Discovery from Data, 2009, 3(2): 8. |
| [5] | Kernighan B W, Lin S. An efficient heuristic procedure for partitioning graphs[J]. Bell Systems Technical Journal, 1970, 49(2): 291-307. |
| [6] | Newman M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6): 066133. |
| [7] | Kossinets G, Watts D J. Empirical analysis of an evolving social network[J]. Science, 2006, 311(5757): 88-90. |
| [8] | Yang T, Chi Y, Zhu S, et al. A Bayesian approach toward finding communities and their evolutions in dynamic social networks[C]//SIAM International Conference on Data Mining. Philadelphia, PA, USA: SIAM, 2009: 990-1001. |
| [9] | Chi Y, Song X, Zhou D, et al. Evolutionary spectral clustering by incorporating temporal smoothness[C]//Proceedings of the 13th ACM International Conference on Knowledge Discovery and Data Mining. New York, NJ, USA: ACM, 2007: 153-162. |
| [10] | Wu Z A, Cao J, Wu J J, et al. Detecting genuine communities from large-scale cocial networks: A pattern-based method[J]. The Computer Journal, 2014, 57(9): 1343-1357. |
| [11] | Papadopoulos S, Kompatsiaris Y, Vakali A, et al. Community detection in social media performance and application considerations[J]. Data Mining and Knowledge Discovery, 2012, 24: 515-554. |
| [12] | Palla G, DeRényi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814-818. |
| [13] | 张长水, 张见闻. 演化数据的学习[J]. 计算机学报, 2013, 36(2): 310-316. Zhang C S, Zhang J W. Learning on time-evolving data[J]. Chinese Journal of Computers, 2013, 36(2): 310-316. |
| [14] | Tantipathananandh C, Berger-Wolf T, Kempe D. A framework for community identification in dynamic social networks[C]//Proceedings of the 13th ACM International Conference on Knowledge Discovery and Data Mining. New York, NJ, USA: ACM, 2007: 717-726. |
| [15] | Tantipathananandh C, Berger-Wolf T. Constant-factor approximation algorithms for identifying dynamic communities[C]//Proceedings of the 15th ACM International Conference on Knowledge Discovery and Data Mining. New York, NJ, USA: ACM, 2009: 827-836. |
| [16] | Tang L, Liu H, Zhang J. Identifying evolving groups in dynamic multimode networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(1): 72-85. |
| [17] | Tang L, Wang X, Liu H. Community detection via heterogeneous interaction analysis[J]. Data Mining Knowledge Discovery, 2012, 25(1): 1-33. |
| [18] | Chakrabarti D, Kumar R, Tomkins A. Evolutionary clustering[C]//Proceedings of the 12th ACM International Conference on Knowledge Discovery and Data Mining. New York, NJ, USA: ACM, 2006: 554-560. |
| [19] | Cao J, Wu Z A, Wu J J, et al. SAIL: Summation-bAsed Incremental Learning for information-theoretic text clustering[J]. IEEE Transactions on Cybernetics, 2013, 43(2): 570-584. |
| [20] | Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113. |



