2. 吉林大学控制科学与工程系, 吉林 长春 130022
2. Department of Control Science and Engineering, Jilin University, Changchun 130022, China
1 引言
如今,汽车工业处于一个闭环主动安全控制的时代,大多数先进的汽车电控系统,如牵引力控制系统(traction control system,TCS)、 防抱死制动系统(anti-lock braking system,ABS)等[1],其控制算法的实现都取决于精确的车辆状态信息. 特别地,轮胎力信息的获取对于增强车辆主动安全性和集成底盘控制[2](unified chassis control,UCC)系统的实现具有重要意义. 然而,车辆现应用的车载传感器无法直接测量车辆的轮胎力信息,这就需要设计估计器作为虚拟传感器应用于汽车电控系统.
一般来说,轮胎纵向/侧向力可以通过估算或估计的方法获得[3, 4, 5, 6, 7, 8, 9, 10]. 对于估算,有以下2种方法: 通过适用于实时计算的简单的轮胎模型获得; 通过包含横摆角速度、 侧向加速度等测量输入的相关动力学方程获得. 而估计的方法在轮胎特性的线性范围内更加准确,常见的方法是设计出不同的估计算法,如卡尔曼滤波(Kalman filter,KF)、 滑模观测器(sliding mode observer,SMO)和非线性观测器.
近几年,学者们针对车辆轮胎与路面之间的纵向力与侧向力的估计做了许多研究和实验,但都具有一定的计算复杂性. 文[11]分别基于单轨和4轮车辆模型构造观测器,运用扩展卡尔曼滤波方法(extended Kalman filter,EKF)估计轮胎力,从而在不需要轮胎力模型的情况下提供满意的轮胎力估计值. 文[12]利用计算得到的轮胎法向力和EKF计算得到的系统状态,通过Dugoff轮胎力模型估计轮胎力. 文[13]设计了一种联合轮胎力估计方案,运用一个随机行走的卡尔曼滤波器来补偿纵向/侧向轮胎力估计器,并将提出的估计方案集成到UCC系统. 文[14]基于单轨车辆模型设计了SMO来估计轮胎力,并对SMO的收敛性进行了讨论. 文[15]提出了一种针对四轮独立转向、 驱制动车辆系统的最优纵向和侧向轮胎力分配方案,最大程度地优化轮胎的使用,实现车辆运动的目标响应. 文[16]提出了一种基于新的神经网络的估计方案,降低轮胎力估计器对于车辆模型不确定性的敏感度.
近年来,由于结构简单、 鲁棒性好等特点,干扰/未知输入观测器已经成为了控制工程中研究的主要课题之一,无论是在传递函数域还是状态空间域都广泛地使用了干扰观测器的方法. 干扰/未知输入观测器(unknown input observer,UIO)作为一种扩展状态观测器,将未知输入或干扰列入到要观测的状态变量中,因此其估计干扰的基本概念类似于一般状态观测器,但是用干扰估计量补偿实际干扰与状态观测器不同. 其补偿基于高增益反馈原理,因而能有效地消除内部及外部干扰. 它的重要性已经体现于各种不同的实际应用中,如轨道牵引系统[17]、 磁推轴承系统[18]、 机械臂[19]等. 此外,干扰观测器也是故障检测系统设计[20]的一种主要方法. 然而,这种方法在车辆状态估计方面的应用依然很少.
为了简便、 快捷、 准确地获取轮胎力的估计值,通过阅读大量相关文献,本文基于车辆动力学模型,以车载传感器测量信号作为输入,设计一种以纵向轮胎力为未知干扰输入项的干扰观测器,并给出推导过程及稳定性分析; 再根据车辆动力学关系,以纵向轮胎力的估计值为输入项之一,估计轮胎的侧向力; 最后,进行离线仿真实验,与估计轮胎力常用的方法EKF做对比分析,验证本文轮胎力级联估计方法的有效性.
2 车辆动力学建模2.1 纵向轮胎力
在纵向轮胎力的估计过程中应用了单轮滚动动力学模型,如图 1所示.
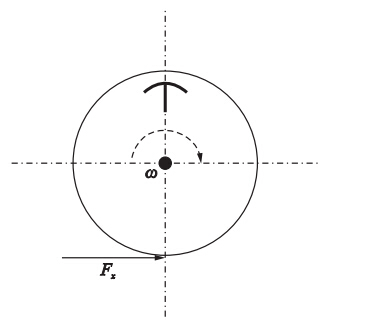 |
| 图 1 车轮动力学模型Fig. 1 Dynamics model of a single wheel |
车辆的每个车轮的动力学方程可以用式(1)表示:
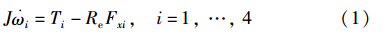
其中,J为车轮转动惯量,ωi为第i个车轮的滚动速度,Re为轮胎有效半径,Fxi为第i个轮胎的纵向力,Ti为第i个车轮驱动与制动力矩的总和. ωi可以通过车载传感器测量得到,但测量值的微分将加大测量噪声,很大程度地降低了估计值的准确性,所以对于车轮纵向力的估计值不能通过车轮滚动的动力学方程直接得到,需要设计一种观测器来避免测量值ωi的微分误差.
2.2 侧向轮胎力考虑整车纵向、 侧向和横摆运动的动力学特性,选取结构简单又能准确地描述本文侧向轮胎力估计问题的3自由度(DOF)平面车辆模型,如图 2所示.
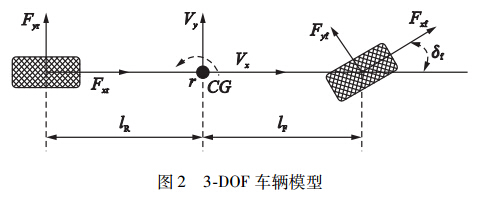 |
| 图 2 3-DOF车辆模型Fig. 2 3-DOF vehicle dynamics model |
车辆y轴和横摆方向的动力学方程用式(2)表示:
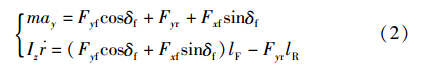
其中,m为车辆质量,ay为车辆侧向加速度,δf为前轮转角,Iz为车辆沿z轴的转动惯量,r为横摆角速度,lF/lR为车辆质心到前后轴的距离,Fxf代表了车辆前轴两侧纵向轮胎力的和,Fyf和Fyr分别代表了车辆前后轴两侧侧向轮胎力的和.
3 估计方案当车辆行驶在有纵向坡度或横向倾斜度的道路上时,车载传感器的测量精度可能会受到影响,所以本文假设车辆行驶在平直路上,也就是说,忽略了车辆的侧倾和俯仰运动的影响. 图 3描述了本文的整体估计方案,由车辆纵向和侧向轮胎力的估计方法设计两部分组成.
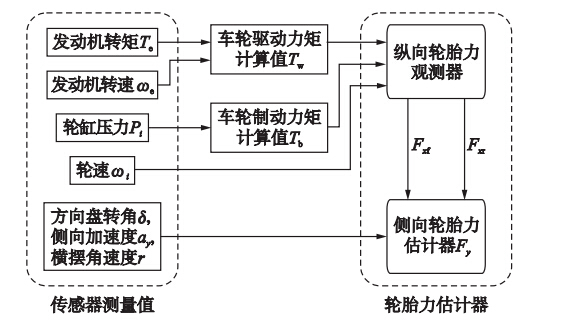 |
| 图 3 轮胎力估计器结构Fig. 3 Structure of the tire force estimator |
纵向轮胎力的估计以车轮驱动/制动力矩和车轮角速度信号作为输入量. 车轮驱动/制动转矩信号不能直接从车载传感器测量得到,但可以从所测量的发动机扭矩和转速与轮缸的压力信号计算得到,为了便于分析和描述本文所关心的车辆轮胎力估计问题,本文假设车轮驱动/制动力矩信号可以直接得到.
将纵向轮胎力的估计值作为输入信号之一输入到侧向轮胎力估计器,形成级联估计器,所以纵向轮胎力估计值的准确性在一定程度上也将影响侧向轮胎力的估计效果. 除此之外,侧向轮胎力的估计所需要的传感器信号包括方向盘转角、 侧向加速度和横摆角速度. 车辆方向盘转角δ与前轮转角δf的关系可以用式δf=δ/Isw表示,Isw为转向传动比.
3.1 纵向轮胎力估计根据文[21, 22]中干扰观测器和摩擦力观测器设计的理论,摩擦力的恒定稳态幅值的估计值具有渐近指数稳定性. 事实上,可以看出,对于一个定向运动,车辆轮胎力观测器可以看成是一个比例误差估计器. 根据车轮滚动动力学方程,对车辆的每个车轮可以设计如式(3)所示的标准观测器,也就是干扰/未知输入观测器估计纵向轮胎力. 未知输入观测器法的基本原理是产生状态估计误差,这种状态估计误差与未知输入干扰(或噪音)变量相解耦. 为了消除未知干扰的影响,首先,对干扰矢量进行重构; 然后,在状态方程中通过重构的干扰项来解耦干扰.
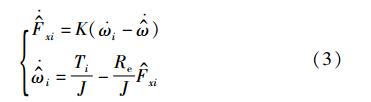
根据纵向轮胎力与轮速的微分的直接的动力学关系,将轮速的微分i作为估计纵向轮胎力的校正量,反馈增益为K,即该干扰估计量正比于观测器状态与系统真实状态之间的误差. 随着t→∞,估计值ω^·无限接近真值i.
为避免对测量信号ωi进行微分带来的估计误差,设正实数ρi,常微分方程变量χi,令ρi=-ReJK,χi=-ρii,则车辆纵向轮胎力的观测器可以转化为

纵向轮胎力作为一个干扰输入项,变量χi的动态特性为

结合车轮滚动动力学方程,纵向轮胎力估计值的动态特性可以表示为式(6):
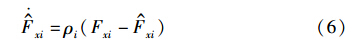
综上所述,车辆纵向轮胎力的干扰观测器的最终表达形式如式(7)所示:

观测得到,该干扰观测器中估计变量i的动态特性由已知系统状态与干扰估计值F^xi结合获得. 实验表明,增益ρi应该足够大,以加快估计响应,同时减少轮胎纵向力的估计误差,下面给出该估计方法的稳定性分析[23].
选取李亚普诺夫函数为
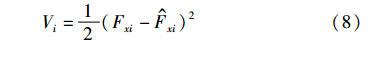
当估计系统稳定时,有V·i≤0,结合式(6),可以得到式(9):
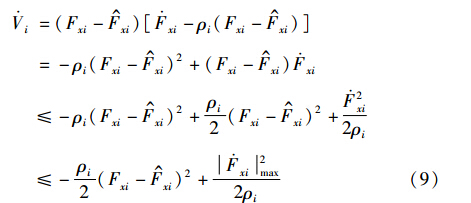
从而得到纵向轮胎力的估计误差的界为
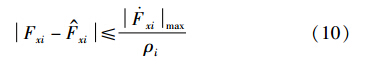
本文可以得出结论: 在该干扰输入全维状态观测器中,作为干扰项的状态变量并不跟踪系统状态,即干扰估计量动态独立于系统状态估计动态,并且该干扰观测器的结构可以被系统地扩展,可以在未来扩展出更多系统所需的高阶项.
3.2 侧向轮胎力估计根据车辆动力学关系式(2),轮胎侧向力的估计值可以根据纵向力的估计值计算得到. 将车辆动力学系统方程转换为矩阵的表达形式,如式(11)所示:
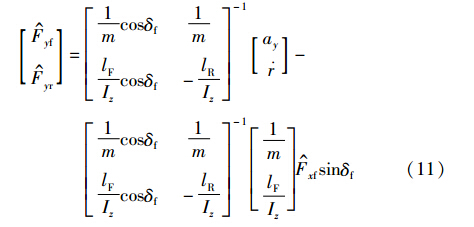
其中,
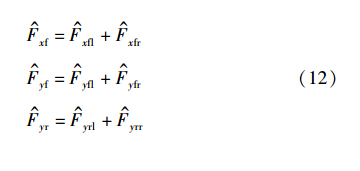
4 仿真实验
本节将通过2种车辆行驶的典型工况对前面给出的轮胎力估计方法进行仿真和验证. 应用高保真的车辆动力学软件veDYNA的整车模型进行仿真研究,其中用到的车辆参数如表 1. 通过调节干扰观测器增益ρi的大小获得最佳的轮胎纵向力估计值. 此外,为了对比本文轮胎力级联估计方法与常用的扩展卡尔曼滤波器(EKF)方法[24]的估计性能,同时将EKF方法应用于本文的车辆模型,选取最佳初值状态,并在同样的条件下与本文方法的估计结果进行比较.
| 符号 | 单位 | 值 |
| m | kg | 1 296 |
| lF | m | 1.25 |
| lR | m | 1.32 |
| J | kg·m2 | 0.8 |
| Iz | kg·m2 | 1 750 |
| Re | m | 0.288 |
考虑车辆行驶在平直的沥青路面上,路面摩擦系数μ=0.8,开始时车辆一直加速到100 km/h,之后保持匀速直线运动稳定行驶,纵向车速的变化过程如图 4所示.
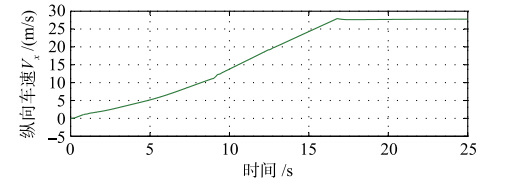 |
| 图 4 纵向车速Fig. 4 Longitudinal vehicle velocity |
将本文干扰观测器估计得到的纵向轮胎力与EKF估计值作对比(车辆轮胎力真值如估计对比图中的实线所示),得到的前后轮的纵向轮胎力估计结果与估计误差如图 5、 6所示. 由于车辆系统的对称性,本文只给出了左侧轮胎力的估计结果,其中仿真曲线的明显振动是由行驶换挡过程引起. 可以用式(13)相应地计算轮胎力估计偏差的均值与方差:

两种估计方法的各轮胎力估计值都是同时估计得到的,利用本文轮胎力级联估计方法,经过数据统计,前左轮的轮胎纵向力的估计偏差的均值与方差分别为27.123 07 N、 14.198 8 N,后左轮的轮胎纵向力的估计偏差的均值与方差分别为13.129 39 N、 626.946 25 N.
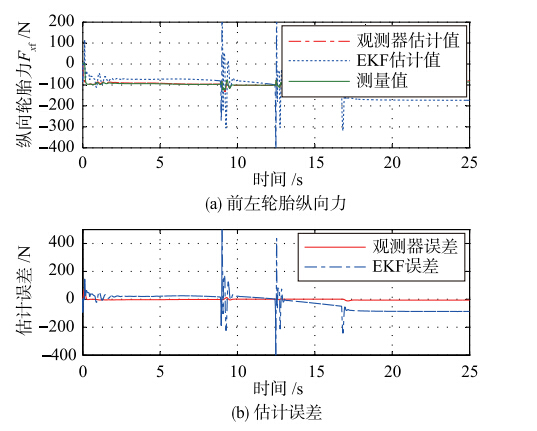 |
| 图 5 直线加速行驶的估计结果Fig. 5 Simulation results of the linear acceleration operation |
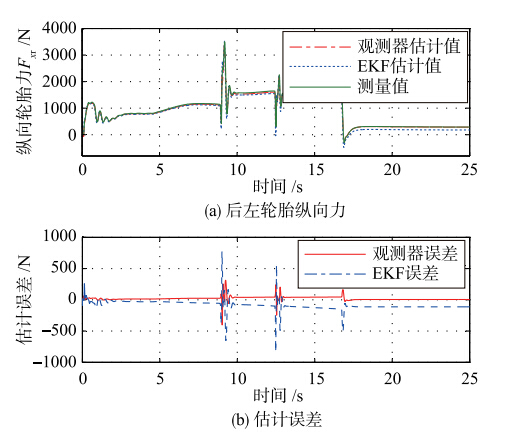 |
| 图 6 直线加速行驶的估计结果Fig. 6 Simulation results of linear acceleration operation |
仿真结果说明,通过两种估计方法得到的轮胎纵向力都存在一定误差,但EKF前轮估计值在车辆行驶换挡过程中振荡更明显. 本文仿真对象为后轮驱动的传统车辆,存在严重机械振动,由于换挡瞬间车辆时变系统非线性很强,容易产生估计滞后,也会导致估计发散,这时EKF估计性能极不稳定,这也是采用EKF方法进行汽车行驶状态参数估计,在实车应用中有待解决的关键问题. 而本文干扰观测器取得了较好的实验结果,实时性更强,在一定程度上说明了估计的有效性.
4.2 常规双移线实验考虑车辆行驶的一种典型工况,激发轮胎侧向特性: 沥青路面上(μ=0.8)的双移线行驶工况,具体运动过程如下: 开始时车辆直线加速到目标车速80 km/h,之后进入双移线操作,最后保持匀速直线运动稳定行驶.
仿真行驶路径及方向盘转角的大小如图 7、 8所示.
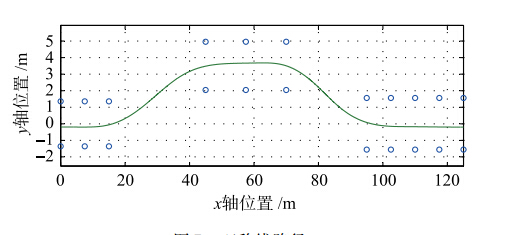 |
| 图 7 双移线路径Fig. 7 Double lane change path |
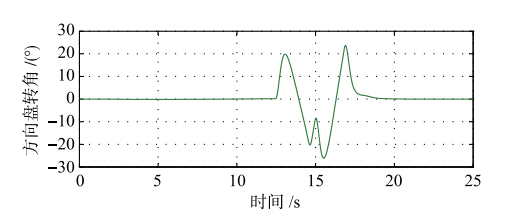 |
| 图 8 方向盘转角Fig. 8 Steering wheel angle |
实验得到的前后轮的纵向轮胎力估计值对比结果与估计误差如图 9、 10所示,轮胎侧向力的估计值对比结果与估计误差如图 11、12所示.
 |
| 图 9 前左轮胎双移线工况的仿真结果Fig. 9 Simulation results of the double lane change of the front-left wheel |
利用本文轮胎力级联估计方法,经过数据统计,前左轮的轮胎纵向力的估计偏差的均值与方差分别为-4.480 21 N、 54.442 89 N,后左轮的轮胎纵向力估计偏差的均值与方差分别为8.692 06 N、 839.379 52 N. 前轴的轮胎侧向力的估计偏差的均值与方差分别为-0.005 33 N、 766 N,后轴的轮胎侧向力的估计偏差的均值与方差分别为0.001 36 N、 690 N.
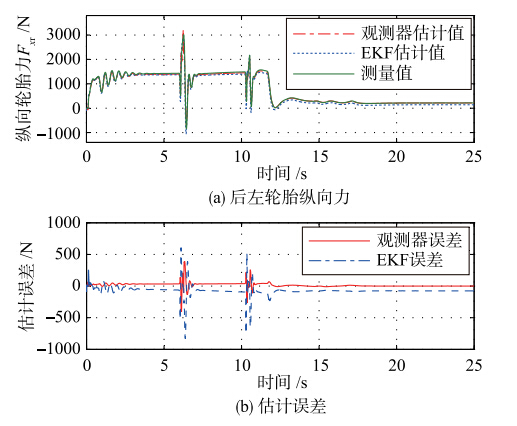 |
| 图 10 后左轮胎双移线工况的仿真结果Fig. 10 Simulation results of the double lane change of the rear-left wheel |
 |
| 图 11 前轴双移线工况的仿真结果Fig. 11 Simulation results of the double lane change of the front axle |
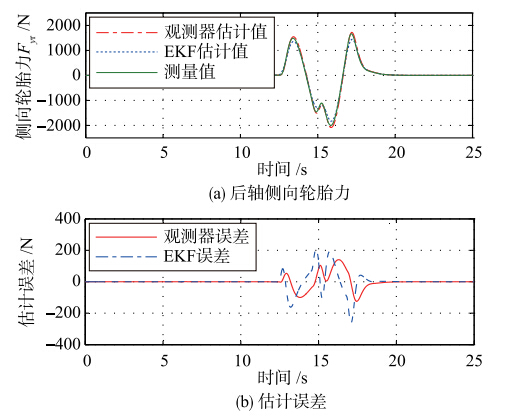 |
| 图 12 后轴双移线工况的仿真结果Fig. 12 Simulation results of the double lane change of the rear axle |
仿真结果在一定程度上说明了本文轮胎力级联估计器的有效性. 与直线加速实验类似,当车辆行驶换挡,产生较大机械振动时,轮胎力估计结果产生较大瞬时静差. 整体轮胎力估计值的动态响应与真实值保持一致,但后轮的纵向轮胎力估计效果要比前轮好,与轮胎力真值相比,干扰观测器对轮胎力的估计结果比EKF更加准确. 如图 11、12所示,两种方法对轮胎侧向力的估计效果相似,都比较良好.
5 结论为了充分地获取车辆信息,提高车辆的主动安全控制性能,本文提出了一种级联的轮胎力估计方法,推导并应用了一种干扰/未知输入观测器的方法来估计轮胎纵向力. 实验表明,这种方法适用于高精度的车辆仿真模型或实车. 另外,利用常用的车载传感器,以轮胎纵向力的估计值作为输入量之一,根据车辆动力学的关系进一步地估计轮胎侧向力. 车辆行驶过程的建模往往包含高阶滤波器,具有计算复杂性,这种分散式的估计结构对于解决车辆状态和参数的严重耦合问题具有很大优势.
仿真结果表明,与EKF方法相比,非线性观测器方法更加灵活,计算量小,更能满足实时性要求,适合实车使用. 本文的估计方法在仿真实验中估计效果优于EKF,具有一定的实时性和有效性.
在今后的工作中,可以尝试引入系统状态的积分校正项来减少静态误差,提高观测结果的精度,满足工程应用的要求. 此外,可以进一步将本文的估计方法应用于四轮独立驱动电动汽车的轮胎力估计,并在实验室的xPC-Target试验台架进行在线仿真实验,进一步验证和提高算法的估计精度.
| [1] | Kang M, Li L, Li H, et al. Coordinated vehicle traction control based on engine torque and brake pressure under complicated road conditions[J]. Vehicle System Dynamics, 2012, 50(9): 1473-1494. |
| [2] | Cho W, Yoon J, Yim S, et al. Estimation of tire forces for application to vehicle stability control[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 638-649. |
| [3] | Baffet G, Charara A, Dherbomez G. An observer of tire-road forces and friction for active security vehicle systems[J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(6): 651-661. |
| [4] | Ono E, Asano K, Sugai M, et al. Estimation of automotive tire force characteristics using wheel velocity[J]. Control Engineering Practice, 2003, 11(12): 1361-1370. |
| [5] | Kim J, Kim S. Estimation of lateral tire force from objective measurement data for handling analysis[R]. Washington, ML, USA: SAE, 2013. |
| [6] | Ray L R. Nonlinear state and tire force estimation for advanced vehicle control[J]. IEEE Transactions on Control Systems Technology, 1995, 3(1): 117-124. |
| [7] | M'sirdi N K, Rabhi A, Zbiri N, et al. Vehicle-road interaction modelling for estimation of contact forces[J]. Vehicle System Dynamics, 2005, 43(s1): 403-411. |
| [8] | Hsiao T, Liu N C, Chen S Y. Robust estimation of the friction forces generated by each tire of a vehicle[C]//American Control Conference. Piscataway, NJ, USA: IEEE, 2011: 5261-5266. |
| [9] | Faraji M, Majd V J, Saghafi B, et al. An optimal pole-matching observer design for estimating tyre-road friction force[J]. Vehicle System Dynamics, 2010, 48(10): 1155-1166. |
| [10] | Acarman T. Observation of vehicle states by using steering wheel angle and wheel angular speeds[C]//IEEE International Conference on Vehicular Electronics and Safety. Piscataway, NJ, USA: IEEE, 2008: 189-194. |
| [11] | Baffet G, Charara A, Lechner D, et al. Experimental evaluation of observers for tire-road force, sideslip angle and wheel cornering stiffness[J]. Vehicle System Dynamics, 2008, 46(6): 501-520. |
| [12] | Dakhlallah J, Glaser S, Mammar S, et al. Tire-road forces estimation using extended Kalman filter and sideslip angle evaluation[C]//Proceedings of IEEE American Control Conference. Piscataway, NJ, USA: IEEE, 2008: 4597-4602. |
| [13] | Cho W, Yoon J, Yim S, et al. Estimation of tire forces for application to vehicle stability control[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 638-649. |
| [14] | Baffet G, Charara A, Lechner D. Experimental evaluation of a sliding mode observer for tire-road forces and an extended Kalman filter for vehicle sideslip angle[C]//Proceedings of the IEEE 46th Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2007: 3877-3882. |
| [15] | Mokhiamar O, Abe M. Simultaneous optimal distribution of lateral and longitudinal tire forces for the model following control[J]. Journal of Dynamic Systems, Measurement, and Control, 2004, 126(4): 753-763. |
| [16] | Matuko J, Petroic' I, Peric' N. Neural network based tire/road friction force estimation[J]. Engineering Applications of Artificial Intelligence, 2008, 21(3): 442-456. |
| [17] | Iannuzzi D, Rizzo R. Disturbance observer for dynamic estimation of friction force in railway traction systems[C]//Proceedings of the IEEE 29th Annual Conference on Industrial Electronics Society. Piscataway, NJ, USA: IEEE, 2003: 2979-2982. |
| [18] | Chen X, Su C Y, Fukuda T. A nonlinear disturbance observer for multivariable systems and its application to magnetic bearing systems[J]. IEEE Transactions on Control Systems Technology, 2004, 12(4): 569-577. |
| [19] | Katsura S,Matsumoto Y,Ohnishi K. Modeling of force sensing and validation of disturbance observer for force control[J]. IEEE Transactions on Industrial Electronics,2007,54(1): 530-538. |
| [20] | Zhang P,Ding S X. Disturbance decoupling in fault detection of linear periodic systems[J]. Automatica,2007,43(8): 1410-1417. |
| [21] | Do K D. Control of nonlinear systems with output tracking error constraints and its application to magnetic bearings[J]. International Journal of Control,2010,83(6): 1199-1216. |
| [22] | Kim K S,Rew K H,Kim S. Disturbance observer for estimating higher order disturbances in time series expansion[J]. IEEE Transactions on Automatic Control,2010,55(8): 1905-1911. |
| [23] | Wang R,Wang J. Actuator-redundancy-based fault diagnosis for four-wheel independently actuated electric vehicles[J]. IEEE Transactions on Intelligent Transportation Systems,2014,15(1): 239-249. |
| [24] | 苏海涛. 汽车非线性轮胎力的估计方法研究[D]. 长春: 吉林大学,2007. Su H T. Research on the methods of vehicle nonlinear tyre forces estimation[D]. Changchun: Jilin University,2007.. |



