2. 中国人民解放军93115部队, 辽宁 沈阳 110031;
3. 中国科学院大学, 北京 100049
2. PLA 93115, Shenyang 110031, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
PID控制因调节方便、 易于工程化等特点,在过程控制、 机电系统控制等多种领域已经获得了广泛的应用[1, 2, 3, 4]. 在实际PID控制系统的参数设计中,一般具有两组最佳整定参数,即“干扰抑制最佳参数”和“伺服跟踪最佳参数”,两组参数在数值上相差甚远. 由此产生了系统设计中的性能指标间的矛盾[5, 6].
为了解决这一性能指标间的矛盾,通常采用2自由度控制方法[7, 8, 9, 10, 11, 12, 13, 14, 15]. 所谓2自由度控制,是指将控制器分解为两部分,然后采用适当的设计方法,找到两组独立的参数并设计出两个独立的控制器,分别用来获得最优的目标跟踪值特性和干扰抑制特性,从而达到控制系统的期望特性.
关于2自由度控制系统的设计方法包括: 内模控制的方法[7, 8]、 级联控制的方法[9, 10]、 基于前置预滤波器的方法[11]、 基于事件的方法[12, 13, 14, 15]等.
事实上,由于2自由度控制系统中两个控制器的相对独立性,它们可以很方便地分别采用不同的方法来设计.
设计使某一个特定的指标达到最优的PID控制器是容易的. 比如,在不考虑伺服跟踪性能的情况下,采用Ziegler-Nichols设计方法[16, 17],可以获得具有优良的扰动抑制性能的单自由度PID控制系统. 在此基础上,通过设计前置预滤波器,即可在不改变系统扰动抑制能力的前提下使系统具有良好的伺服跟踪性能. 因此,前置预滤波器的研究,具有重要的工程实际意义.
常见的前置预滤波器包括低通滤波器[18, 19]与时滞滤波器[21, 22]. 然而,低通滤波器只能滤除高频振动,对于中低频震荡则不起作用; 而时滞滤波器则一般只适用于2阶开环系统,且会带来系统响应中的时间延迟.
本文提出一种面向2自由度PID控制系统的基于最小二乘法的前置预滤波器设计方法. 采用本方法,能够在没有系统模型的情况下,基于系统的响应输出曲线进行前置预滤波器的设计. 所设计出的前置预滤波器能使有效减小2自由度PID控制系统在阶跃响应中的震荡,且能使系统的响应速度与预设的参考模型的响应速度一致. 从而简化了2自由度PID控制系统的设计,并确保了所设计的系统具有良好的伺服响应特性.
2 2自由度控制系统的基本结构图 1给出了2种典型的2自由度控制系统结构. 其中,r(t)为参考输入信号,d(t)为负载扰动输入,y(t)为系统输出,C1(s)、 C2(s)、 Ca(s)及Cb(s)为控制器的各个组成模块,G(s)为被控对象.
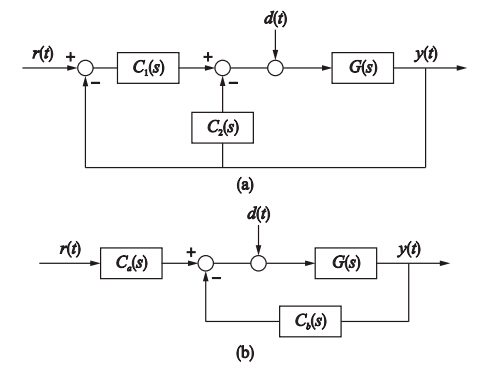 |
| 图 1 两种典型的2自由度控制系统结构图Fig. 1 Structures of two typical 2-DOF control systems |
不同结构的2自由度控制系统是可以相互转换的,如令:
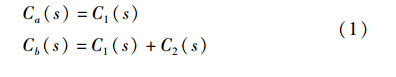
则图 1所示的2个控制系统是完全等价的. 其它结构的2自由度控制系统也可以通过类似的方法进行等价转换.
本文基于图 1(b)所示的2自由度控制系统结构,研究当Ca(s)与Cb(s)为PID型控制器时,Ca(s)与Cb(s)的设计方法.
令:

其中,KaP、 KaI、 KaD分别表示前馈控制器的比例、 积分、 微分系数; KbP、 KbI、 KbD分别表示反馈控制器的比例、 积分、 微分系数. 图 1(b)所示的2自由度控制系统化为图 2所示的结构.
 |
| 图 2 2自由度PID控制系统的结构图Fig. 2 Structure diagram of 2-DOF PID control system |
图 2所示控制系统分为2个部分: 对参考输入信号进行预处理的前馈控制器F(s)及包含了被控对象的闭合回路部分H(s).
3 系统的伺服跟踪性能设计3.1 系统输出的分解
图 3所示系统为图 2中的2自由度PID控制系统的一种等价结构. 其中,H(s)为图 2所示系统中包含被控对象的闭合回路部分.
 |
| 图 3 对2自由度PID控制系统的系统输出进行分解的结构图Fig. 3 Structure diagram of system output decomposition of 2-DOF PID control system |
根据图 3,该2自由度控制系统的输出信号可以分解为
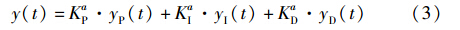
其中,yP(t)、 yI(t)和yD(t)定义为系统输出的分量.
3.2 参考模型在控制器设计中,需要根据执行器的输出能力、 系统的响应速度等因素来决定控制系统的带宽. 假设控制系统的带宽与阻尼系数的设计目标为ωn,可以建立如下参考模型:
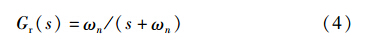
不失一般性,Gr(s)也可以设定为具有相应带宽的2阶系统或其它符合动态特性要求的系统.
不考虑扰动信号的影响,对于相同的系统参考输入r(t),假设图 3所示系统的输出信号为y(t),Gr(s)的输出信号为yr(t). 显然,yr(t)为理想的系统响应输出,因此定义为参考响应输出.
线性定常系统的传递函数定义为系统输出的拉氏变换与输入信号的拉氏变换之比. 因此在系统初始状态为零的前提下,系统的传递函数(即动态特性)由系统的阶跃响应输出唯一确定[16, 17]. 因此,要使目标系统的动态特性接近于Gr(s),只需要使y(t)尽可能地接近于yr(t). 为此,设计如下代价函数:
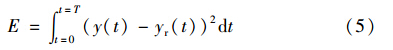
其中,T为选定的用于确定积分范围的时间点,T的值应该足够大,使得y(t)与yr(t)能够在[0,T]的时间范围内完成动态过程.
根据上述论述,设计目标转化为: 如何计算出能够使得E取得最小值的KaP、 KaI与KaD的值.
3.3 基于最小二乘法的参数设计根据3.1节中的系统输出分解,将式(3)代入式(5)得
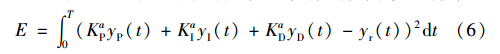
根据最小二乘法,式(6)取得最小值的充要条件是:
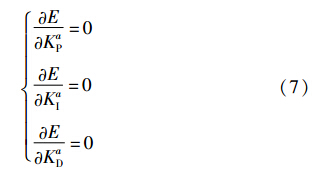
即:
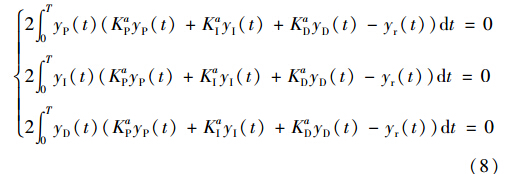
定义:
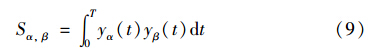
其中α,β∈{P,I,D}.
根据Sα,β的定义,显然有:

这意味着,由式(9)给出的9个参数,只需计算其中的6个.
对于yr(t),定义:
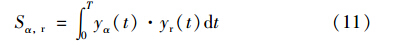
其中α∈{P,I,D}.
将式(9)和(11)代入式(7),得到取得最小值的充要条件:
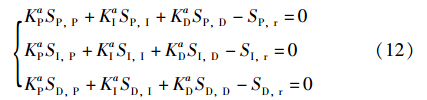
式(12)中的各个S的意义由式(11)给出. 因此,只需要根据式(9)和式(11)计算出Sα,β和Sα,r的值,并将其代入式(12),即可计算出能够使得E取得最小值的KaP、 KaI与KaD的值.
在实际应用中,往往需要利用式(9)和式(11)的离散形式,即:
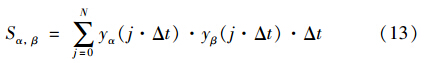

其中,Δt=T/N.
在式(12)所给出的3个方程两边同时乘以或除以同一个常数,方程仍然成立,因此为了简化计算,可以将Sα,β和Sα,r重新定义为
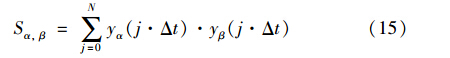
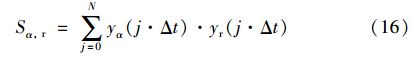
3.4 系统静态增益的校正
尽管采用上述方法能够得到使E取得最小值的KaP、 KaI与KaD的值,从而使得图 2所示系统的动态特性尽可能地接近于参考模型. 但是,一般情况下E的最小值不等于0,即y(t)与yr(t)之间总是存在差别的,而这种差别可能导致图 2所示系统的静态增益不等于1,即系统的输出存在静态误差.
由于前置预滤波器只对参考输入信号进行处理,与系统的反馈回路无关,因此上述静态误差与外部扰动及测量误差无关,而且是由滤波器参数决定的确定值. 所以这个问题是容易解决的. 一个简单的解决方法是: 在上述参数设计完成之后,对所得系统的静态增益进行测量辨识,然后将所设计的前馈控制器F(s)乘以静态增益的倒数即可. 系统的静态增益的测量辨识是容易的.
4 仿真在仿真中所采用的被控对象的传递函数为P(s)=1/(s+1)3. 首先采用方法设计一个具有良好扰动抑制性能的PID控制器,其传递函数为C(s)=4.8+2.65/s+2.11s. 构成的控制系统如图 4所示.
尽管采用(Ziegler Nichols)法设计的PID控制系统具有良好的扰动抑制能力,但其伺服跟踪性能较差. 图 7中的曲线1给出了上述单自由度PID控制系统的阶跃响应曲线,其超调约为40%.
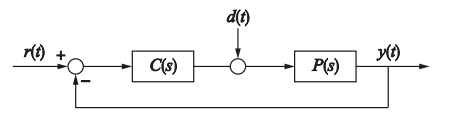 |
| 图 4采用N-Z法设计的单自由度PID控制系统Fig. 4 Single degree PID control system designed by N-Z method |
为了改善控制系统的伺服跟踪性能,在上述设计基础上,进一步设计2自由度PID控制系统. 其基本结构如图 5所示.
 |
| 图 5 2自由度PID控制系统的基本结构图Fig. 5 Basic structure of 2-DOF PID control system |
在图 5所示控制系统中,控制器Cb(s)即为图 4所示系统中的C(s)、 Ca(s)的传递函数:
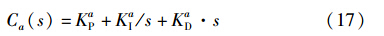
其中KaP、 KaI与KaD为所要设计的参数.
参考模型选择为

将图 5所示系统结构变换为图 3所示的形式. 将系统的阶跃响应输出的各个分量以0.1 s的周期进行采样,采样时间为T=40 s. 系统响应输出的分量如图 6所示.
将系统响应输出的分量信号采样数据代入式(15)与式(16)可得
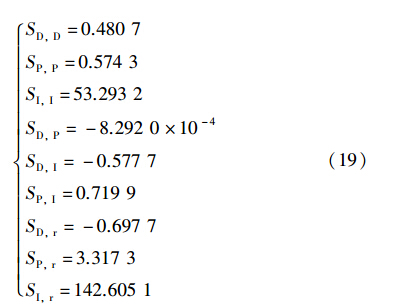
将式(19)给出的结果代入式(12)可得:
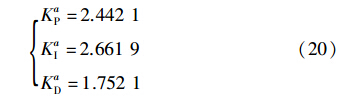
将式(20)代入式(17),并将所得Ca(s)应用于图 5所示的2自由度PID控制系统,所得系统的阶跃响应输出如图 7中的曲线2所示.
比较图 7中的曲线1与曲线2可见,所设计的2自由度PID控制系统,其阶跃响应输出中的振荡及超调量显著变小; 比较曲线2与曲线3可知,所设计系统的阶跃响应输出与参考模型的阶跃响应输出非常相近.
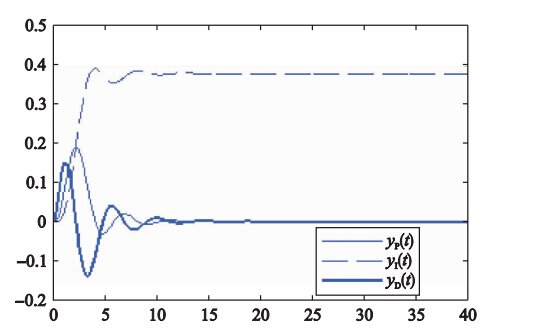 |
| 图 6 系统响应输出的分量信号Fig. 6 Component signals of system output |
 |
| 图 7 各系统的阶跃响应输出曲线比较Fig. 7 Comparison of step response outputs among various systems |
通过对曲线2的稳态值进行测量可知,所得系统的稳态增益为1.004 5,因此Ca(s)的最终设计结果为
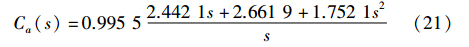
为了验证本文所提前置预滤波器的效果,将所设计的上述滤波器与其它方法设计的滤波器的滤波效果进行比较. 由于时滞滤波方法只适用于欠阻尼开环系统的预滤波,在对于闭环系统的前置预滤波问题上无法作为比较对象,因此比较对象选取两个不同阶数的低通滤波器. 其传递函数分别为


相应的控制系统的整体结构如图 8所示,其中,F(s)为F1(s)或F2(s).
 |
| 图 8 采用低通滤波器的PID控制系统的结构图Fig. 8 Structure of PID control system with pre-filter |
当图 8所示系统中的F(s)采用F1(s)和F2(s)时,系统的阶跃响应输出分别为图 9中的曲线2和曲线3. 对比可得,采用本文所提出的前置预滤波方法所得系统的阶跃响应中的振荡和超调明显小于采用低通滤波方法所得的结果.
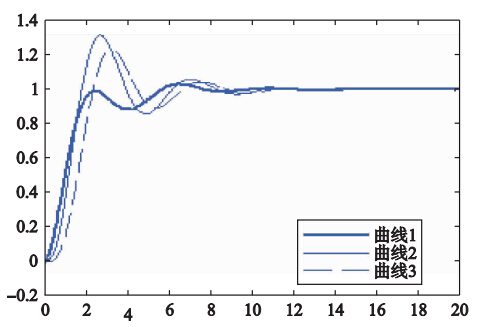 |
| 图 9 前置预滤波器的滤波效果比较Fig. 9 Filtering effect comparison of the pre-filters |
为了对所设计的前置预滤波器进行鲁棒性验证,将所设计的Ca(s)的KaP、 KaI与KaD的值分别增加10%,并进行阶跃响应仿真,所得的系统响应输出曲线如图 10所示. 其中,曲线1对应初始前置预滤波器,曲线2对应将KaI增大10%并调整稳态增益后的系统输出,曲线3和曲线4分别对应将KaP与KaD增大10%后的系统输出. 由图可见,当滤波器参数变化10%后,系统响应输出的变化较小,滤波器的滤波效果仍明显优于由式(22)和式(23)给出的低通滤波器. 由此可见,所提方法具有较好的鲁棒性.
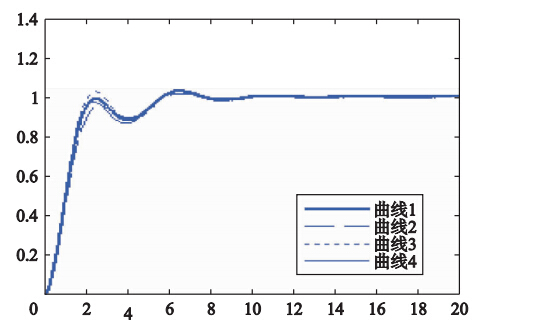 |
| 图 10 前置预滤波器参数变化后的系统响应输出曲线Fig. 10 System output curves after the variation of pre-filter parameters |
5 结论
本文提出了一种基于2自由度控制思想的改进PID控制系统伺服跟踪性能的设计方法. 该方法基于最小二乘法原理,能够使系统的阶跃响应输出尽可能地接近于参考模型的阶跃响应输出. 仿真结果表明,采用该设计方法能够显著减小系统阶跃响应输出中的振荡与超调,从而改善系统的伺服跟踪性能. 通过系统阶跃响应输出曲线的比较可得,所提方法的滤波效果明显优于采用前置预滤波器的滤波效果. 最后通过仿真验证了所提方法具有良好的鲁棒性.
| [1] | 宋彦, 赵盼, 陶翔, 等. 基于μ综合的无人驾驶车辆路径跟随串级鲁棒控制方法[J]. 机器人, 2013, 35(4): 417-424. Song Y, Zhao P, Tao X, et al. UGV robust path following control under double loop structure with μ synthesis[J]. Robot, 2013, 35(4): 417-424.. |
| [2] | 刘楠楠, 石玉, 范胜辉. 基于Pareto 最优的PID 多目标优化设计[J]. 信息与控制, 2010, 39(4): 385-390. Liu N N, Shi Y, Fan S H. PID multi-objective optimization design based on Pareto optimality[J]. Information and Control, 2010, 39(4): 385-390.. |
| [3] | 胡志强, 周焕银, 林扬, 等. 基于在线自优化PID 算法的USV 系统航向控制[J]. 机器人, 2013, 35(3): 263-268. Hu Z Q, Zhou H Y, Lin Y, et al. The course control based on an on-line self-adjusted PID control algorithm for unmanned surface vehicle[J]. Robot, 2013, 35(3): 263-268. . |
| [4] | 葛金来, 张承慧, 崔纳新. 模糊自整定PID 控制在三自由度直升机实验系统中的应用[J]. 信息与控制, 2010, 39(3): 342-347. Ge J L, Zhang C H, Cui N X. Fuzzy self-tuning PID controller in the 3DOF helicopter experimental system[J]. Information and Control, 2010, 39(3): 342-347. . |
| [5] | Alcantara S, Vilanova R, Pedret C. PID control in terms of robustness/performance and servo/regulator trade-offs: A unifying approach to balanced autotuning[J]. Journal of Process Control, 2013, 23(4): 527-542. |
| [6] | Huba M. Performance measures, performance limits and optimal PI control for the IPDT plant[J]. Journal of Process Control, 2013, 23(4): 500-515. |
| [7] | Liu T, Gao F R. Enhanced IMC design of load disturbance rejection for integrating and unstable processes with slow dynamics[J]. ISA Transactions, 2011, 50: 239-248. |
| [8] | Alfaro V M, Vilanova R. Model-reference robust tuning of 2DoF PI controllers for first-and second-order plus dead-time controlled processes[J]. Journal of Process Control, 2012, 22(2): 359-374. |
| [9] | Liu T, Gu D Y, Zhang W D. Decoupling two-degree-of-freedom control strategy for cascade control systems[J]. Journal of Process Control, 2005, 15(2): 159-167. |
| [10] | Alfaro V M, Vilanova R, Arrieta O. Robust tuning of Two-Degree-of-Freedom (2-DoF) PI/PID based cascade control systems[J]. Journal of Process Control, 2009, 19(10): 1658-1670. |
| [11] | Cerone V, Milanese M, Regruto D. Robust feedforward design for a two-degrees of freedom controller[J]. Systems & Control Letters, 2007, 56(11/12): 736-741. |
| [12] | Sancheza J, Visioli A, Dormidoa S. A two degree of freedom PI controller based on events[J]. Journal of Process Control, 2011, 21(4): 639-651. |
| [13] | Krebs G, Tounzi A, Pauwels B, et al. Modeling and control of a 2DoF PM synchronous actuator using Hall effect sensors[J]. Mechatronics, 2010, 20(1): 153-161. |
| [14] | Alfaro V M, Vilanova R. Robust tuning of 2DoF five-parameter PID controllers for inverse response controlled processes[J]. Journal of Process Control, 2013, 23: 453-462. |
| [15] | Cao B C, Sarkar P P. Identification of rational functions using two-degree-of-freedom model by forced vibration method[J]. Engineering Structures, 2012, 43: 21-30. |
| [16] | Åström K J, Hgglund T. PID controllers: Theory, design and tuning[M]. New York, USA: Instrument Society of America, 1995: 151-163. |
| [17] | Ogata K. Modern control engineering[M]. 3rd ed. New York, USA: Prentice Hall, 2001: 263-272. |
| [18] | Cole M O T. A class of low-pass FIR input shaping filters achieving exact residual vibration cancelation[J]. Automatica, 2012, 48(9): 2377-2380. |
| [19] | Economou D, Mavroidis C, Antoniadis I, et al. Maximally robust input preconditioning for residual vibration suppression using low-pass FIR digital filters[J]. Journal of Dynamic Systems, Measurement, and Control, 2002, 124(2): 85-97. |
| [20] | 梁春燕, 李旻智, 谢剑英. 抑制柔性机械臂残留振荡的时滞滤波器设计[J]. 控制与决策, 2001, 16(6): 943-946. Liang C Y, Li M Z, Xie J Y. Time delay filter design to eliminate residual vibration of flexible beam[J]. Control and Decision, 2001, 16(6): 943-946. . |
| [21] | 王晓军, 邵惠鹤. 鲁棒最优随机时滞滤波器的频域设计方法[J]. 控制与决策, 2006, 21(10): 1172-1176. Wang X J, Shao H H. Design of robust optimal arbitrary time-delay filter in the frequency domain[J]. Control and Decision, 2006, 21(10): 1172-1176. . |
| [22] | 梁春燕, 钟庆昌, 谢剑英. 时滞滤波器抑制残留振荡: 理论、方法及应用[J]. 控制与决策, 2006, 21(10): 263-269. Liang C Y, Zhong Q C, Xie J Y. Time delay filter to reduce residual vibration: Theory, methods and applications[J]. Control and Decision, 2006, 21(10): 263-269. . |



