2. 北京交通大学先进控制系统研究所, 北京 100044
2. Advanced Control Systems Laboratory, Beijing Jiaotong University, Beijing 100044, China
1 引言
高速列车自动控制(ATC)系统用于实现列车的运行指挥功能,是列车高效、 安全运行的重要保障. ATC系统的重要功能之一是实现高速列车的自动停车,即列车在期望停车点处准确停车以保障行车安全. 现阶段高速列车的停车控制是通过分布式空电混合制动系统实现的. 制动系统通过调节各机车的电制动和空气制动的介入比,使整个列车获得一致、 稳定的制动性能[1]. 另外,高速列车的实际制动过程还要受理想制动曲线的约束. 因此,自动停车控制器应当以分散的空电混合制动控制系统为设计基础,以理想停车曲线为参考,实现高速列车的自动精确停车功能.
高速列车自动停车控制器实际设计中需要考虑以下因素[1]: 首先,高速列车各车厢间通过弹性车钩连接,因此在列车制动过程中,各节车厢会受到车钩弹力和阻尼力的影响. 其次,列车制动过程中不确定非线性阻力同样会降低列车的停车精度. 列车运行速度越高,其所受的阻力越大,阻力的非线性越明显. 最后,列车制动力表现为空气制动力和电制动力的联合作用,控制器设计需要同时考虑这两个系统的特点.
许多先进的控制策略应用到动车组ATC控制器的设计中以克服上述问题. 为处理高速列车自身的非线性特性,控制器设计通常采用智能化的方法,如模糊控制、 神经网络控制和多模型预测控制[2, 3, 4]. 为消除列车运行过程中所受不确定阻力的影响,智能化的自适应控制策略得到了应用,并取得良好的仿真效果[5, 6, 7]. 文[8]基于Pade近似,处理了具有输入时滞的线性制动系统模型. 对于高速动车组的巡航控制,文[9, 10]提出基于线性模型辨识(LMI)方法的鲁棒巡航控制器. 上述方法虽然均取得了良好的控制效果,但是仍缺少不同速度条件下对于制动模型动态特性的分析.
高速列车制动模型本质为非线性大系统模型[10, 11]. 由于大系统模型的复杂性,其控制器设计通常采用智能化的方法. 文[12, 13, 14]将非线性模型表示为T-S模糊模型,并基于状态观测器及自适应、 鲁棒等策略设计了分布式模糊控制器,取得了良好的仿真效果. 为实现对参考信号的追踪,滑模控制方法应用到了控制器设计中[15, 16, 17, 18, 19]. 文[16, 17]中,作者将自适应方法、 智能控制策略与滑模控制相结合,克服了大系统模型中参数化的不确定性和非线性特性等因素的影响. 基于T-S模糊模型,Chiang将模糊滑模控制器推广到具有状态时滞、 输入时滞的系统中[18, 19]. 但是,上述文献由于缺少对实际应用背景的分析,导致其使用受到限制.
本文基于大系统观点,提出了一种基于自适应模糊策略的自动停车滑模控制器,用以消除制动过程中车间作用力、 不确定非线性阻力的影响,提高列车的停车精度. 首先,建立了描述列车制动系统动态特性的非线性大系统模型,并将该模型转化为T-S模糊模型进行处理; 其次,提出了分布式自动停车滑模控制器,该控制器采用自适应模糊系统用于逼近模型中互联项及不确定项的上界; 最后,利用Matlab软件对制动系统进行了仿真实验. 仿真结果验证了所提算法的有效性.
2 高速列车制动模型2.1 高速列车动力学方程
基于大系统观点,高速列车纵向动力学分析如图 1所示. 图中,高速列车共n节车厢,mi表示第i节车厢的质量; xi=[xi,1,xi,2]T表示每节车厢的状态变量,其中xi,1为第i节车厢的位置,xi,2为第i节车厢的速度; ki、 di分别表示第i个车钩的弹性系数和阻尼系数; l为相邻车厢间的自然距离,具体为列车长度、 车钩原始长度及车钩间隙; bi为第i节车厢轮轨间的制动力; Rr,i为第i节车厢轮轨间的滚动阻力; Ra为空气阻力,其主要作用在第1节车厢.
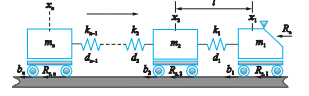 |
| 图 1 高速列车受力分析示意图Fig. 1 Force diagram of high speed train |
车钩系统的作用在于车厢间传递纵向牵引/制动力,从而使列车作为一个整体运行. 实际中,车钩力主要表现为弹性力和阻尼力. 第i节车厢与i+1节车厢间的车钩力Fc为[10, 11]
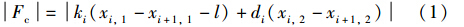
列车制动过程中受到的阻力分为滚动阻力和空气阻力. 每节机车都会受到轮轨间滚动阻力的影响,而空气阻力则主要作用在第1节机车. 第i节车厢所受的滚动阻力Rr,i的经验公式为

式中,c0、 cv为常数.
第1节车厢所受空气阻力Ra的经验公式为
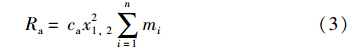
式中,ca为常数. 由式(2)和式(3)可知,运行阻力在高速条件下的非线性较强. 在实际应过程中,受运行环境影响,阻力Rr,i和Ra包含外界扰动,具有不确定性.
高速列车制动系统采用空电混合制动方式. 对于第i节机车,在高速区段制动力bi主要表现为电制动力; 低速区段则主要为空气制动力. 空气制动力的大小与闸瓦摩擦系数成正比. 由于闸瓦摩擦系数受材料、 环境等因素的影响,故其实际值μi会偏离设计值μi′,导致空气制动力的实际值与设计值的比值为μi/μi′. 因此,在不同速度条件下,不同制动系统的制动力施加效果也是不同的.
根据上述分析,n节车厢的高速列车动力学方程可以表示为
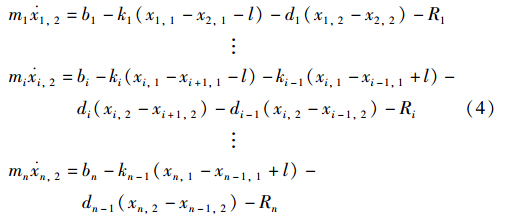
式中,当i=1时,R1=Ra+Rr,1; 当i≠1时,Ri=Rr,i. 由于阻力包含不确定扰动且为速度的非线性函数,因此Ri为不确定的非线性项.
2.2 高速列车T-S模糊模型大系统(4)中,第i个子系统可以抽象表示为
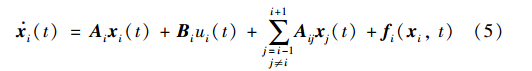
式中,状态向量xi=[xi,1,xi,2]T且满足i,1=xi,2; ui为控制器输出,表示自动停车控制器发出的制动减速度指令; Ai为系统矩阵,其形式为 Ai=01-kimi-ki-1mi-dimi-di-1mi (i=2,3,…,n),A1=01-k1m1-d1m1; Bi=σ0μi/μi′+(1-σ)01,σ为空气制动作用在整个制动系统中的比例; Aij为互联矩阵,其形式为Ai,i-1=00ki-1midi-1mi (i=2,3,…,n),Ai,i+1=00kimidimi (i=1,2,…,n-1); fi(t)为不确定项,其具体表达式为f1(x1,t)=0-R1(x1,t)+k1l,fi(xi,t)=0-Ri(xi,t)+kil-ki-1l (i=2,3,…,n-1),fn(xn,t)=0-Rn(xn,t)-kn-1l. 将非线性模型(5)表示为T-S模糊模型. 根据列车运行速度,第i个子系统、 第m条规则Rmi为

式中,规则分为高速区间规则(m=2)和低速区间规则(m=1); Fmi为对应的模糊集合,即F1i为低速区间集合,F2i为高速区间集合; Ami、 Bmi和Amij均为常数矩阵, Ami=01ami,1ami,2,Bmi=0bmi,2,Amij=00amij,1amij,2,m=1,2; 非线性扰动fmi(xi,t)=0Δfmi,2,m=1,2,Δfmi,2为未知函数. 高速列车制动速度分布整体论域区间为[0, 50](m/s),低速模糊集合为F1i={ν|0≤ν≤40},高速模糊集合为F2i={ν|10≤ν≤50},其中ν为列车运行速度. 针对子系统i,模糊集合的隶属度函数ωmi,m=1,2,如图 2所示.
 |
| 图 2 T-S模糊模型隶属度函数Fig. 2 Membership functions of T-S fuzzy model |
隶属度函数ωi=[ω1i,ω2i]T,满足ωmi(t)≥0且∑2m=1ωmi(t)=1. 隶属度函数表示当列车速度较低时,系统主要表现为低速模型; 当速度较高时,系统更接近高速模型.
因此,高速列车非线性大系统模型表示为
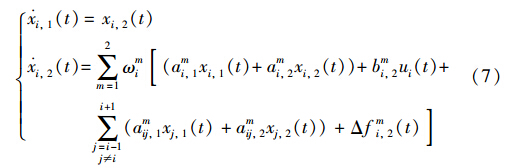
3 自适应模糊滑模停车控制器设计
3.1 高速列车自动停车控制器设计目标
高速列车自动停车控制器的重要功能是使列车具有较高的停车精度. 在实际应用中,为保证列车制动过程的平稳性,控制器应当使列车追踪匀减速制动曲线. 参考信号xmi(t)=[xmi,1(t),xmi,2(t)]T用来描述第i节车厢理想停车曲线且满足mi,1(t)=xmi,2(t).
假设1 第i节车厢的参考信号xmi(t)为连续且有界的,即xmi(t)∞≤δi,其中δi为常数.
自动停车控制器设计目标为: 利用高速列车分散制动的条件,设计分布式滑模制动控制器ui(t),i=1,2…,n,在满足列车实际制动约束的前提下,使得各子系统的实际制动过程跟踪理想制动曲线,即使各子系统追踪误差渐近收敛于0.
3.2 高速列车自动停车控制器为提高控制器的鲁棒性[18],对模型中互联项以及不确定项作为整体进行处理,即定义:

根据式(8),列控大系统的第i个子系统(7)可进一步表示为
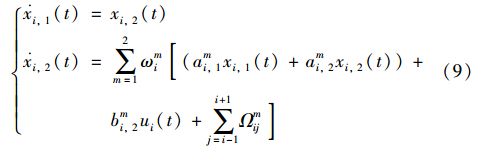
针对第i个子系统的参考信号,定义追踪误差ei(t)=xi(t)-xmi(t),可得误差系统:
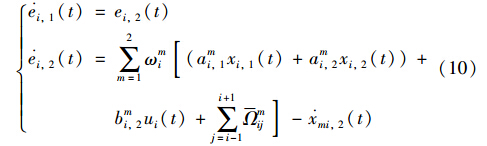
为对消系统中第i个子系统中的确定项,选取控制器为

式中,ua,i为鲁棒项.
将控制器(11)代入误差系统(10),可得
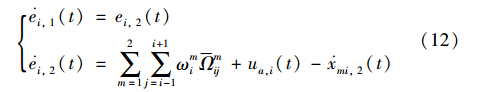
根据式(12),为使系统追踪误差渐近收敛于0,针对第i个子系统,选取滑模面:

式中,ci,1>0.
由于系统(12)中存在不确定项,因此需要设计控制器中的鲁棒项ua,i,使滑模面Si渐近收敛于0. 鲁棒项可以通过自适应模糊推理系统得到.
假设2 根据式(8),互联项和不确定项在制动过程中是有界的且满足:
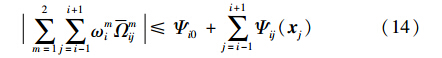
式中,Ψi0为未知常数,Ψij(xj)为未知函数.
针对式(14)中存在未知参数Ψi0和未知非线性函数Ψij(t),本文采取自适应策略来处理这一问题. 具体地,引入自适应增益项Ψ^i0逼近不确定增益项Ψi0; 根据模糊逼近引理[17, 18],引入模糊系统Ψ^ij(xjηij)来逼近未知函数Ψij(t).
模糊推理系统采用三角隶属度函数模糊化、 乘积推理规则和中心解模糊化,其形式为

式中,l为模糊逼近系统的规则,rij为规则总数,Alijk为第l条规则下xj,k的模糊集合,其对应的隶属度函数为μAl ijk ; ηij=[η1ij,η2ij,…,ηrijij]T为权系数. 由式(15)可得模糊系统基函数为
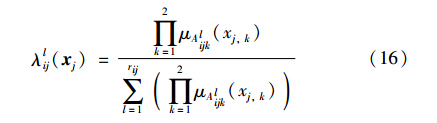
则模糊推理系统表示为
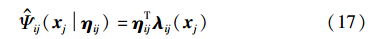
式中,λij(xj)=[λ1ij(xj),λ2ij(xj),…,λrijij(xj)]T为回归向量,ηij=[η1ij,η2ij,…,ηrijij]T∈Λ表示与回归向量对应的参数向量,Λ为包含ηij可行参数集合的紧集.
定义模糊逼近系统的最优参数向量和相应的最小逼近误差:
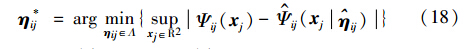
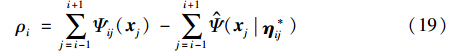
定义估计误差如下:



式中,Ψ^i0、 ij及i为对应参数的估计值.
由滑模面(13)的导数,可得

因此,鲁棒项ua,i(t)选择如下:

式中,αi>0,sgn(·)为符号函数[17].
综上所述,结合式(11)和式(24),高速列车分布式自动停车控制器为
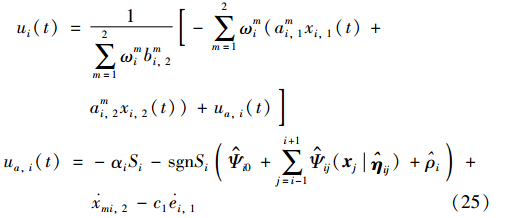
对应地,参数的鲁棒自适应律为

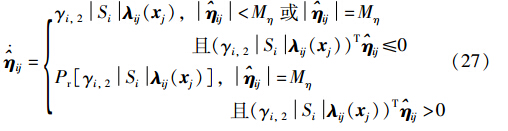

式中, Pr[·]=I-ijTijij2γi,2Siλij(xj),γi,1、 γi,2、 γi,3均为正常数,Mη为已知正常数. 控制器框图如图 3所示,图中∫表示积分器.
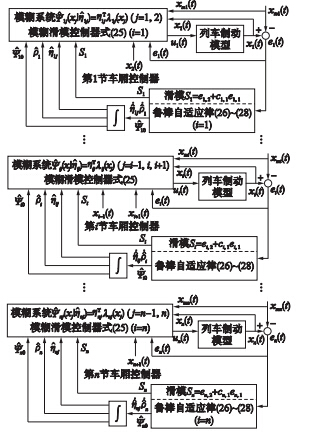 |
| 图 3 控制器设计框图Fig. 3 Design diagram of the controller |
3.3 高速列车自动停车控制器性能分析
针对误差系统(12),选取李亚普诺夫函数:

式中, Vi,1=S2i/2,Vi,2=12γi,12i+12γi,2∑i+1j=i-1Tijij+12γi,32i0.
Vi,1的导数可表示为
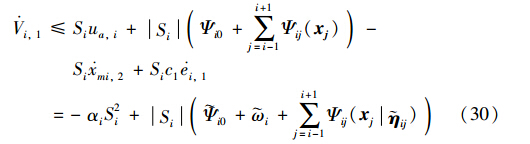
Vi,2导数可以表示为
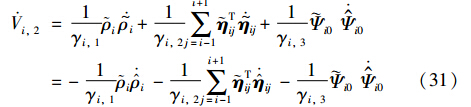
将自适应律(26)~(28)代入式(31),可得
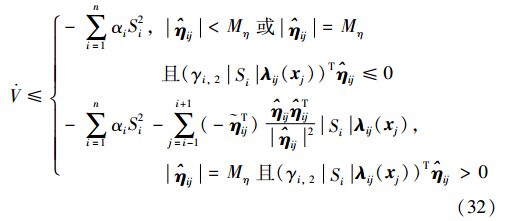
由于-Tijij≥Mη(Mη-η*ij)≥0且TijSiλij(xj)>0,因此∑i+1j=i-1(-Tij)ijTijij2Siλij(xj)>0,则式(32)可进一步化简为

由式(33)系统中全部信号均为有界的,根据Barbalat引理[20],Si∈L2且Si(t)→0,t→∞,因此ei(t)→0,t→∞,所以在控制器(25)的作用下,高速列车的实际停车曲线可以渐近追踪目标曲线.
4 数值仿真在Matlab环境下对高速列车制动情况进行数值仿真实验. 仿真中以“一动一拖”为背景,首车为动车; 高速列车最高制动减速度为-1 m/s2,为保证列车运行的平稳性,实际制动减速度不能超过最高减速度限制[1]; 列车制动的初始速度为162 km/h; 制动过程追踪-0.8 m/s2的匀减速停车曲线,当目标曲线的速度趋于0时,其减速度随速度快速收敛到0; 列车有效制动时间约为56 s,为显示追踪误差和滑模面的收敛性,仿真时间设置为100 s; 制动距离约为1 300 m; 列车初始间距为30 m. 高速列车仿真参数如表 1所示.
第i个子系统的模糊逼近系统Ψ^ij(xjηij)的位移和速度论域分别为[0,1 300](m),[0, 50](m/s). 对于位移定义两个模糊集合Aij11(制动距离近)和Aij12(制动距离远),对于速度定义两个模糊集合Aij21(运行速度高)和Aij22(运行速度低). 选取模糊集合的三角隶属度函数如图 4所示.
 |
| 图 4 模糊系统隶属度函数Fig. 4 Membership functions of fuzzy systems |
模糊逼近系统的规则数rij=4,隶属度函数为
μA1 ij1 (xj,1)=μA2 ij1 (xj,1)=μAij11(xj,1)
μA3 ij1 (xj,1)=μA4 ij1 (xj,1)=μAij12(xj,1)
μA1 ij2 (xj,2)=μA3 ij2 (xj,2)=μAij21(xj,2)
μA2 ij2 (xj,2)=μA4 ij2 (xj,2)=μAij22(xj,2)
在不确定非线性阻力和控制器(25)的作用下,动车追踪误差曲线和减速度曲线分别如图 5和图 6所示.
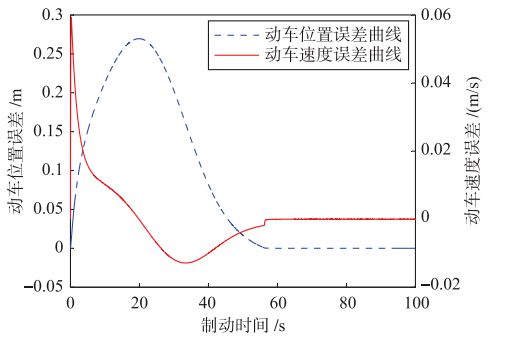 |
| 图 5 动车追踪误差曲线Fig. 5 Locomotive tracking error curves |
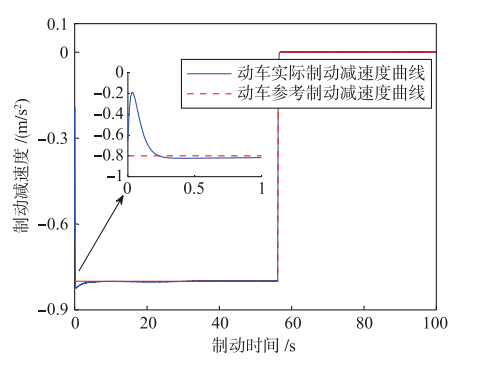 |
| 图 6 动车减速度曲线Fig. 6 Locomotive deceleration curves |
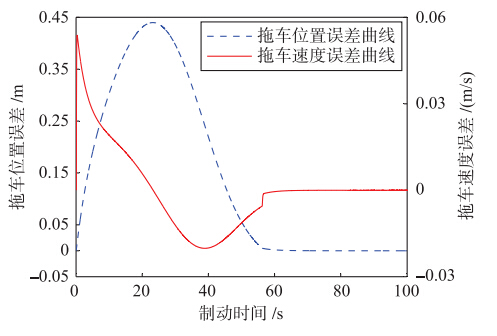
拖车的追踪误差曲线和制动减速度曲线分别如图 7和图 8所示.
 |
| 图 7 拖车追踪误差曲线Fig. 7 Wagon tracking error curves |
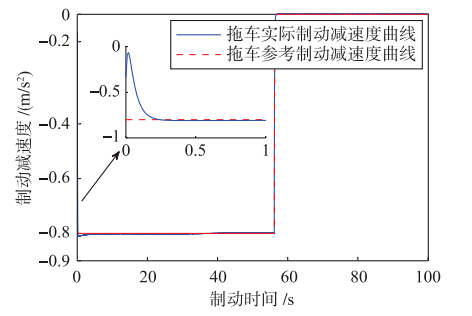 |
| 图 8 拖车减速度曲线Fig. 8 Wagon deceleration curves |
动车和拖车的滑模面变化曲线如图 9所示.
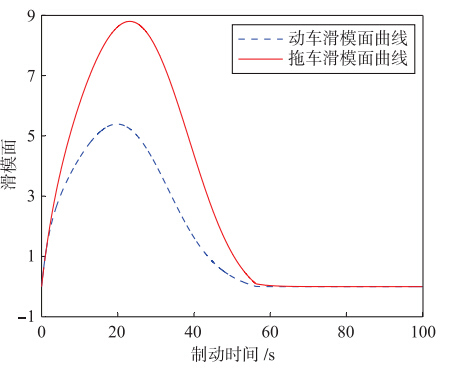 |
| 图 9 滑模面曲线Fig. 9 Sliding mode surface curves |
图 5和图 7显示自动停车控制器克服了制动过程中运行阻力和车间作用力的影响,使得追踪误差渐近收敛到0,实现对理想停车曲线的渐近追踪.
图 6和图 8描述了制动减速度曲线,小图为动态过程的展开显示. 制动过程中,各车厢实际制动减速度经短暂调整均快速收敛到参考减速度值,即-0.8 m/s2; 当列车速度较低,实际制动减速度曲线追踪参考制动减速度快速收敛到0; 列车停车后,动车拖车的实际制动减速度均为0,整个过程满足列车实际制动情况要求. 仿真实验中,动车和拖车的实际制动减速度值均不超过最大制动减速度的限制,保障了高速列车运行的平稳性.
图 9中各车的滑模面均收渐近收敛到0,满足理论分析结果,验证了滑模控制器的正确性.
5 结论本文研究了高速列车自动停车控制器的设计问题. 本文建立了高速列车制动模型,设计了自适应模糊滑模控制器,并基于Matlab/Simulink仿真软件进行了数值仿真实验.
(1) 根据高速列车纵向动力学分析,建立了列车制动非线性大系统模型. 根据列车运行速度,将非线性模型转化为T-S模糊模型. 该模型描述了运行阻力和制动系统在不同制动速度下的动态特性.
(2) 基于自适应模糊策略,设计了高速列车自动停车滑模控制器. 控制器通过设计自适应模糊推理系统,逼近模型中不确定信号和互联项的上界,提高控制精度.
(3) 以“一动一拖”为背景对高速列车制动模型进行仿真实验. 结果表明自动停车算法在获得较高停车精度的同时保障了高速列车运行的平稳性.
因此,该算法对于高速列车实际自动停车控制器的设计,实现ATC自动停车功能,具有较高的参考价值.
| [1] | 王月明. 动车组制动技术[M]. 北京: 中国铁道出版社, 2004: 43-75. Wang Y M. EMU braking technology[M]. Beijing: China Railway Publication House, 2004: 43-75. |
| [2] | Dong H R, Gao S G, Ning B, et al. Extended fuzzy logic controller for high speed train[J]. Neural Computing & Application, 2013, 22(2): 321-328. |
| [3] | 余进, 钱清泉, 何正友. 两级模糊神经网络在高速列车ATO系统中的应用研究[J]. 铁道学报, 2008, 30(5): 52-56. Yu J, Qian Q Q, He Z Y. Research on application of two-degree fuzzy neural network in ATO of high speed train[J].. Journal of the China Railway Society, 2008, 30(5): 52-56. |
| [4] | Zhou Y, Yang X, Mi C. Model predictive control for high-speed train with automatic trajectory configuration and tractive force optimization[J]. Computer Model in Engineering & Sciences, 2013, 90(6): 415-437. |
| [5] | Song Q, Song Y D, Tang T, et al. Computationally inexpensive tracking control of high-speed Trains with traction/brake saturation[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1116-1125. |
| [6] | Song Q, Song Y D. Data-based fault-tolerant control of high-speed trains with traction/braking notch nonlinearities and actuator failures[J]. IEEE Transactions on Neural Networks, 2011, 22(12): 2250-2261. |
| [7] | Song Q, Song Y D, Cai W. Adaptive backstepping control of train systems with traction/braking dynamics and uncertain resistive forces[J]. Vehicle System Dynamics, 2011, 49(9): 1441-1454. |
| [8] | 罗仁士, 王义惠, 于振宇, 等. 城轨列车自适应精确停车控制算法研究[J]. 铁道学报, 2012, 34(4): 64-68. Luo R S, Wang Y H, Yu Z Y, et al. Adaptive stopping control of urban rail vehicle[J]. Journal of the China Railway Society, 2012, 34(4): 64-68.. |
| [9] | Yang C D, Sun Y P. Mixed H2/H∞ cruise controller design for high speed train[J]. International Journal of Control, 2001, 74(9): 905-920. |
| [10] | Chou M S, Xia X H. Optimal cruise control of heavy-haul trains equipped with electronically controlled pneumatic brake systems[J]. Control Engineering Practice, 2007, 15(5): 511-519. |
| [11] | Chou M S, Xia X H, Kayser C. Modelling and model validation of heavy-haul trains equipped with electronically controlled pneumatic brake systems[J]. Control Engineering Practice, 2007, 15(4): 501-509. |
| [12] | Liu Y J, Tong S C, Chen L P. Adaptive fuzzy control via observer design for uncertain nonlinear systems with unmodeled dynamics[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(2): 275-288. |
| [13] | Tong S C, Huo B Y, Li Y M. Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(1): 1-15. |
| [14] | Koo G B, Park J B, Joo Y H. Decentralized fuzzy observer-based output-feedback control for nonlinear large-scale systems: An LMI approach[J]. IEEE Transactions on Fuzzy Systems, 22(2): 406-419. |
| [15] | Islam S, Liu P. Robust sliding mode control for robot manipulators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(6): 2444-2453. |
| [16] | Zhang Y X, Dong H R. Fuzzy-neural network adaptive sliding mode tracking control for interconnected system[J]. Computational Intelligence, 2006, 4114(1): 127-133. |
| [17] | 张严心, 张嗣瀛. 一类非线性互联系统的间接自适应模糊滑模跟踪控制[J]. 自动化学报, 2003, 29(5): 658-665. Zhang Y X, Zhang S Y. Fuzzy indirect adaptive sliding mode tracking control for a class of nonlinear interconnected systems[J]. Acta Automatica Sinica, 2003, 29(5): 658-665.. |
| [18] | Chiang C C. Adaptive fuzzy sliding mode control for time-delay uncertain large-scale systems[C]//44th IEEE Conference on Decision and Control and European Control Conference. Piscataway, NJ, USA: IEEE, 2005: 4077-4082. |
| [19] | Chiang C C. Decentralized robust fuzzy-model-based control of uncertain large-scale systems with input delay[C]//IEEE International Conference on Fuzzy Systems. Piscataway, NJ, USA: IEEE, 2006: 498-505. |
| [20] | Krstic M, Kanellakopoulos I, Kokotvic P. Nonlinear and adaptive control design[M]. New York, USA: Wiley, 1995: 21-25. |



