2. 铁道部信息技术中心, 北京 100860
2. Information and Technologies Center, MOR, Beijing 100860, China
1 引言
为了加快货车的周转速度,编组站通过编制各种计划来组织作业和调度资源. 其中阶段(3 h~4 h)计划是日班计划的分阶段具体安排,也是对调车作业计划的统筹规划,包括配流、 作业排程和资源分配三个相互关联的子问题. 配流是阶段计划的核心,指将现车和计划到达列车中符合货物列车编组计划要求的车流编组生成出发列车. 作业排程主要解决解编顺序问题,是指在满足资源容量限制的情况下实现作业在时间上的排序. 由于不同的作业排程方案会产生不同的车流接续关系,所以有必要在静态配流中考虑作业排程问题,实现动态配流,决策出优化的解编顺序和出发车车流来源.
针对动态配流问题,文[1, 2, 3, 4, 5, 6, 7, 8, 9]分别设计了表上作业方法与遗传的混合算法、 免疫算法、 遗传算法、 局部邻域搜索算法、 拉格朗日松弛算法、 有偏随机键遗传算法、 联赛选择规则与遗传的混合算法、 遗传—蚁群协同求解算法及和声算法求解动态配流整数规划模型. 上述研究都是建立在数学规划(mathematical programming,MP)模型基础上的,只能将约束表示成算术表达式,存在逻辑约束难于量化和计算复杂性过大等问题. 另外有的研究[4, 6, 7, 8, 9]使用加权和法建立多目标规划模型,这种方法需要针对不同的数据确定不同权值,在实际应用中存在目标权值无法确定的问题. 以往的智能算法均未使用约束推理方法来化简模型,求解时间较长,不符合现场对计划编制实时性的要求; 而且将MP模型和求解紧密结合的方法,难以适应编组站作业流程和组织模式变化的情况. 其存在的主要问题有: 有的是在到发车流平衡的前提下以车辆在站总的停留时间最短为目标,但是现场到发车流一般是不均衡的,即不是所有的出发列车都能配流成功,正点发车; 有的在建立班计划平均中停时最小目标时,用车辆的出发时间减去到达时间,这样可能会导致越早到达的车辆越晚出发,延长了一个班时间内平均中停时,应该加以修正; 有的没有充分考虑调车场容量限制和阶段初始时刻的资源不空闲等因素,偏离现场实际需求; 有的只建立了单推单溜解体方式的MP模型,不能适应双推单溜和双推双溜等复杂的作业模型,通用性不好.
针对以往MP理论存在建模困难、 求解效率低和不稳定的问题,本文基于约束程序(constraint programming,CP)[10, 11, 12, 13, 14]的累积调度问题(cumulative scheduling problem,CuSP)[10, 11, 12, 13, 14]和字典序多目标优化(lexicographic multi-objective optimization,LMO)[15]理论,按照配流成功的出发列车优先级总和最大、 车辆平均中停时最小和资源利用率最高3个目标的优先级,建立动态配流字典序多目标累积调度(DWALMCuS)3层模型; 并设计了约束传播(constraint propagation,CPr)[13]和多点构建性搜索(multi-point constructive search,MPCS)[16]的混合算法(CPr-MPCS)迭代求解,每层先通过约束传播化简模型、 缩小搜索空间,再通过带约束传播的多点构建性搜索算法快速求解,决策出优化的作业排程和配流方案. 针对模型存在通用性和适应性低的问题,本文充分考虑现场实际需求,应用CP约束谓词建模方法,修订了目标函数,考虑了调车场总容车量限制和阶段初始时刻资源的实际占用状态,并将整个解体作业划分为推峰和溜放作业,以适应不同解体方式的需求.
2 动态配流模型为了解决多目标加权和法权值无法确定的问题,按照3个目标函数的优先级,建立了动态配流字典序多目标累积调度(DWALMCuS)三层模型,每层都是累积调度(CuSP)模型.
2.1 字典序多目标由于到发车流不均衡,因此,不是所有的出发列车都能配流成功,为了尽量兑现班计划,故主目标为配流成功的出发列车优先级总和最大. 在发车最多的基础上,应该使得先到车先发,加快车辆的周转速度. 另外,当前阶段作业排程时要充分利用资源,为下一阶段动态配流提供良好的资源初始占用状态. 综上所述,建立3个具有字典序的目标:


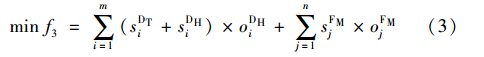
目标(1)为配流成功的出发列车优先级总和最大,其中oFMj∈{0,1}为出发列车fj的编组作业AFMj的执行标志,默认取值为0,当执行时oFMj=1; pEFj为出发列车fj的优先级,根据列车等级(直达>直通>区段>摘挂>小运转)和发车时间唯一确定,n为出发列车数.
目标(2)为在目标(1)的基础上使得到达列车先到先发,等价于车辆在站的平均停留时间最短目标,其中oDHi∈{0,1}为到达列车di溜放作业ADHi的执行标志; pEDi为di的优先级,先到车优先级高,m为到达列车数.
目标(3)为资源利用率最高,其中sDTi=tDi为di接入股道作业ADTi的开始时刻; sDHi∈{tDi+pDTi+pDPi,tDi+pDTi+pDPi+1,…,te-pDHi}为di溜放作业ADHi的开始时刻; sFMj∈{ts,ts+1,…,tFj-pFMj-pFTj}为fj编组作业AFMj的开始时刻.
为了解决线性加权和法在实际应用中权值无法确定导致模型求解不稳定问题,依据现场实际需求和调度员决策偏好建立的字典序多目标模型,并通过带初始解的迭代法[15]依次求得每层的最优解:

2.2 约束
本模型根据现场实际需求,用CP中逻辑约束谓词[13, 14]来表达作业实施逻辑、 作业间的优先级、 满轴、 车流接续、 不违编等约束条件; 用CuS中资源(分为可恢复和不可恢复)容量限制表达式[13, 14]表示车流、 调车场、 到发线、 解编调机、 推送线和溜放线等资源容量约束:
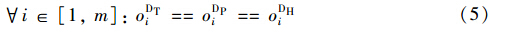

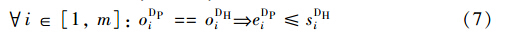
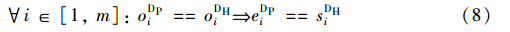
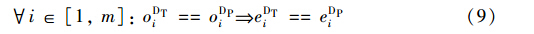
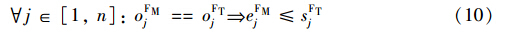
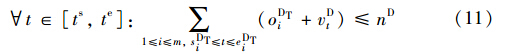
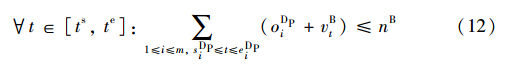
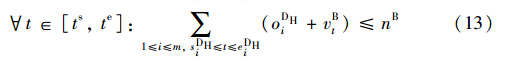
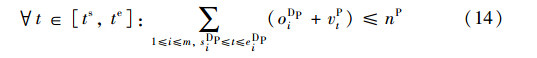
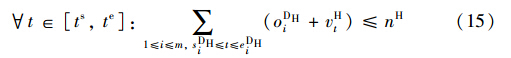
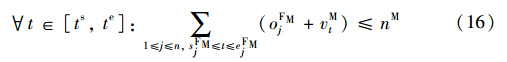
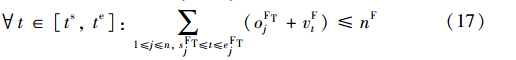
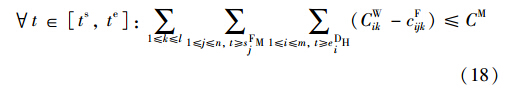
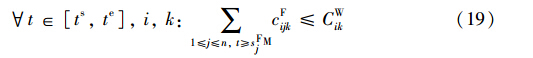



式(5)和式(6)为作业间实施逻辑蕴含约束,是指某作业的执行是以其它作业的执行为前提的; oDTi∈{0,1}为di接入股道作业ADTi的执行标志,默认取值为0,当执行时oDTi=1; oDPi∈{0,1}为di推峰作业ADPi的执行标志,默认取值为0,当执行时oDPi=1; oFTj∈{0,1}为fj接入股道作业AFTj的执行标志,默认取值为0,当执行时oFTj=1.
式(7)为在双推单溜解体方式下,到达车列推峰完毕可能需要等峰再溜放的作业优先级约束. 其中eDPi为di推峰作业结束时刻,等于推峰开始时刻sDPi∈{tDi+pDTi,tDi+pDTi+1,…,te-pDPi-pDHi}与推峰持续时间pDPi之和,tDi为到达时刻,现车的到达时刻为ts,te为阶段技术时刻,pDTi为技术作业持续时间,pDHi为溜放作业持续时间; sDHi∈{tDi+pDTi+pDPi,tDi+pDTi+pDPi+1,…,te-pDHi}为di溜放作业开始时刻,pDPi为推峰作业持续时间.
式(8)为在单推单溜或者双推双溜解体方式下到达车列推峰完毕后,不需要等峰而直接溜放的作业优先级约束.
式(9)为到达列车接入股道和解体作业之间的优先级约束: 在实际作业中,当推峰出了到达场股道的防护信号机时就出清了股道,此时到达车列还没有解体完毕,即股道腾空时刻应该早于解体完毕时刻,但为了保障安全,一般情况下会认为到达列车占用股道结束时刻等于解体结束时刻.
式(10)为出发列车编组结束时间早于接入股道开始时刻的作业优先级约束,eFMj为编组结束时刻,等于编组开始时刻sFMj∈{ts,ts+1,…,tFj-pFMj-pFTj}与编组持续时间pFMj之和,pFTj为出发技术作业持续时间,tFj为发车时刻.
式(11)~(17)为到达场股道、 推送线、 溜放线、 解编调机和出发场股道等资源容量约束,其中nD为到达场股道数,nB为解体调机数,nP为推送线数,nH为溜放线数,nM为编组调机数,nF为出发场股道数; t∈[ts,te],vDt∈[0,nD]、 vBt∈[0,nB]、 vPt∈[0,nP]、 vHt∈[0,nH]、 vMt∈[0,nM]和vFt∈[0,nF]表示在t时刻被占用的到达场股道数、 解体调机数、 推峰线数、 溜放线数、 编组调机数和出发场股道数.
式(18)为调车场容量约束. 其中,cFijk∈{0,1,…,Vj}为fj消耗RWik车辆数,默认取值为0; RWik为di中属性为ωk的车流,CWik∈{0,cDik}为RWik的容量,默认取值为0; {cDik}为到达列车编组内容,cDik表示特征为ωk的车辆数; Ω={ω1,…,ωk,…,ωl}为由到、 发车统计得到的阶段时间内车流方向/车种集合; CM为调车场最多容纳车辆数.
式(19)为车流资源容量约束: 配流过程中,所有出发列车消耗车流数不超过车流资源容量.
式(20)为车流随着到达列车解体而产生的逻辑约束.
式(21)为车流接续和不违编约束. 其中λjk为编组特征值,若编组计划中允许fj可以开行ωk的车,则λjk=1,否则λjk=0.
式(22)为满轴约束: 出发车列必须要达到列车编组计划规定满轴要求,才进行编组作业. 其中Vj为编组的轴重和换长要求,假设每个车辆的轴重和换长近似相等,则满轴条件用车辆数代替.
本模型考虑了到发车流不均衡和调车场容量限制等因素,更接近现场实际需求; 模型使用逻辑表达式实现满轴、 车流接续、 不违编、 资源容量、 作业时态等约束,缩减了模型规模. 模型中考虑双推单溜模式下等峰情况,将整个解体作业分为推送和溜放两部分,所以模型通用性比以前更强. 同时模型的各约束是独立建立的,故扩展性较好.
3 约束传播和多点构建性搜索混合算法编组站DWALMCuS模型按照目标的优先级分为3层,用带初始解的迭代算法(iteration algorithm with initial solution,IAIS)[15]依次求解,主要思路是将上层的最优解作为下层的初始解,并动态增加避免上层目标退化约束以加快搜索. 各子层为NP-Hard问题,首先通过约束传播算法(constraint propagation,CPr)[13]剔除不可能成为解的那部分变量取值,缩小解空间,减少无效搜索. 但是约束传播算法缺乏完备性,不能将部分解扩展成完整解; 同时基本回溯算法(backtracking algorithms,BT)[13]在实例化变量时没有利用任何启发式信息,且未用已实例化变量进行相容性检查避免未来冲突,求解时间较长,故设计了约束传播和多点构建性搜索(multi-point constructive search,MPCS)[13, 16]的结合算法(CPr-MPCS).
3.1 约束传播约束传播算法[13]主要思想是: 当变量论域被修改时,所有与其相关的变量都要调用减域算法修改论域,如此反复,直到所有变量的论域都约减到最小. 约束传播包括减域(domain reduction,DR)[13]和传播两部分.
3.1.1 减域算法减域是指为了满足约束,由某一个变量的有限取值推导出其它变量只能取某些值,而达到论域约减的目的. 针对式(11)~(18)累积资源约束,使用ILOG CP Optimizer提供的基于边缘搜索(edge-finding)策略[10, 11, 12, 13]的累积资源约束减域算法. 对于剩余约束,使用ILOG CP Optimizer提供的弧边界相容(Arc-B-Consistency)[10, 13]减域算法,此算法不对变量论域中所有取值进行相容性检查,只检查变量论域的上下界,避免了不必要的相容性检查,比基本弧相容(arc consistency)算法效率更高[13].
记模型的变量集为X,变量论域集为D,约束集为C,D(xi)为变量xi∈X的论域,X(ci)为约束ci包含的变量集,目标函数为min f,最大变量论域度max{D(xi)}=d,最大约束度为max{X(ci)}=r,约束数C=e. 根据复杂度理论计算得到基于边缘搜索(edge-finding)策略的累积资源约束减域算法时间复杂度为O(kn2),其中k为作业中不同资源容量需求; 在最坏情况下弧边界相容约束传播算法的时间复杂为O(ed),而基本弧相容约束传播算法的时间复杂度为O(erdr),所以Arc-B-Consistency算法效率更高.
3.1.2 约束传播算法步骤步骤1 输入X、 D和C,生成约束传播队列Q←{(c,x)|c∈C & x∈X(c)}.
步骤2 如果Q=,返回“约束传播结束”; 否则,从Q中依次选择并删除(c,x).
步骤3 调用减域算法修订x的值域D(x). 如果D(x)= ,返回“无解”; 如果D(x)被修改,则转步骤4; 如果D(x)不变,转步骤2.
步骤4 在Q中增加弧: Q←Q∪{(c′,x′)|c′∈C\c&x∈X(c′)& x′∈X(c′)& x′≠x},转步骤2.
3.2 约束传播和多点构建性搜索的混合算法(CPr-MPCS)类似于进化算法,多点构建性搜索算法不断地迭代精英解(elite solution),当达到搜索资源(内存容量、 迭代次数、 CPU时间、 失败次数等)界限时重启回溯算法,它是在重启算法(randomized restart,RR)基础上扩展形成的算法框架,在其中可以引入先进的技术来提高求解效率[16],求解效率高于RR算法和BT算法.
3.2.1 初始约束传播在启动搜索算法求最优解之前调用约束传播算法,对变量的论域进行约减,如果存在某个变量x∈X,使得D(x)= ,则返回“无解”,否则返回约减后的变量论域集D′.
3.2.2 变量动态排序的启发方法为了提高回溯算法的效率,除了通过约束传播缩小解空间,还可以使用变量动态排序启发式(variable ordering heuristics,VarOH)[13]算法对未实例化变量进行排序,为分支选择提供决策支持,使得较早地检测出冲突. 本研究根据最先失败原则,采用基于变量论域大小的启发式方法,即优先选择D(xi)最小的xi作为下一个分支,如果最小论域的变量不唯一,则按既定次序选择.
3.2.3 带约束传播技术的多点构建性搜索在多点构建性搜索中引入约束传播技术可以用已实例化变量进行相容性检查避免未来冲突,缩小了决策变量的临时论域,加快了求解效率. 如下所示为带约束传播技术的MPCS算法步骤:
步骤1 初始化精英解集合E;
步骤2 如果未达到总的求解时间,转步骤3,否则返回精英解集合E中使得f最小的解e作为最优解或者满意解;
步骤3 从精英解集合E中随机选择一个精英解e,转步骤4;
步骤4 令O为通过精英解e得到的目标值,添加约束f
步骤6 调用带精英解的回溯算法S(e,b),得到解s,转步骤7;
步骤7 如果s比e更优,则用s替代e,转步骤2.
1) 精英解. 解是变量实例化的集合s={〈x1=v1〉,…,〈xm=vm〉},m≤n,其中n为变量数,vi∈D(xi)为变量xi的取值. 精英解是之前搜索过程中实例化变量数最大的局部解或者目前最好的可行解. 精英解集合基数E对整个算法的求解效率影响很大,解的质量、 求解时间和空间成本与E成正相关,经过测试E取为15.
2) MPCS算法终止条件. 根据列车的到发强度可得到法场车流变化频率大概为每次几分钟; 技术作业图表(运站1)中时间轴单位为min,表示车站调度员可以忽略的阶段计划时间误差也为几分钟; 根据调研得知车站调度员对阶段计划自动编制可接受的时间上限平均为2 min,而编组站阶段计划内容不仅包括出发列车动态配流还有直通列车接入股道、 配流剩余到解列车接入股道和解体、 调车场股道活用等. 综合考虑上述因素确定编组站动态配流求解时间界限为2 min左右,其中第1层求解时间为60 s,第2层和第3层求解时间均为30 s.
3) S(e,b)算法失败次数上界. 为了解决BT算法很难从分支中恢复而导致效率低的问题,引入了重启策略[16]: 当深度搜索失败次数达到上界后重新启动搜索,本轮的失败界限是上一轮的若干倍,如此循环,直至在规定时间内找到最优解或者满意解. 经测试,设定初始失败次数rfl为120,失败次数增长率rgf为1.15.
4) S(e,b)算法中变量的实例化. S(e,b)在实例化变量xi时要优先查看其是否在e中已被实例化,如果已经实例化且vi∈D(xi),则令xi=vi; 如果xi不在e中或者xi在e中但viD(xi),则通过取值排序启发式(value ordering heuristics,ValOH)算法[13]选择优先级最高的值vi∈D(xi)来实例化xi=vi.
5) 带精英解的回溯算法S(e,b). 回溯算法是基于搜索树的深度优先遍历法. 搜索树是由一系列的选择点〈xi=vi〉∨〈xi≠vi〉组成的,令精英解e={〈x1=v1〉,…,〈xm=vm〉},m≤n. 则S(e,b)算法思路: 首先通过变量动态排序算法VarOH选择论域最小的变量xi作为下一个实例化变量. 然后,调用约束传播算法对与xi相关联的且未实例化的变量进行约束传播,如果存在D(xk)= ,则回溯,否则返回所有变量论域集合D; 如此不断地在精英解e的基础上迭代实例化变量,当达到此轮搜索失败次数界限,则返回新的解s.
CPr-MPCS算法在搜索之前,利用约束传播技术将不可能是变量的可行解的值从该变量的初始值域中剔除,以减少算法的无效搜索. 在搜索过程中,由某个变量赋值导致临时论域的变化而触发约束传播算法对其它相关未实例化变量临时论域的约减,加快了搜索.
某编组站有一个到达场、 一个调车场和两个出发场,其中调车场和2个出发场横列式排列,采用双推单溜解体方式,解体调机数为2,到达场股道数为14,编组调机数为3,出发场股道数为26,调车场最大容车数为4 000辆. 选取2013年8月15日12∶00编组场现车与12∶00-15∶00之间的计划到达列车为到达列车数据. 根据车站“站细”及实际作业经验得到: 到达技术作业时间标准为60 min,出发技术作业时间标准为30 min,到解车推峰时间标准为15 min,溜放时间标准为15 min,编组作业时间标准为60 min. 为了充分测试,选取3 h阶段时间内计划到达15列到解车; 由于现车也可以编组形成出发车,所以计划出发车数可取为20列.
在双推单溜解体方式下,假设列车等间隔到达,那么可以计算最后1列最早解体完毕时刻为16∶42. 如果最后1列到达车可以为最后1列出发车提供车流,则可得到最后1列出发车的发车时刻大概为19∶30. 再考虑实际作业中列车并非等间隔到发,则根据以上分析估计得到: 根据12∶00-15∶00阶段内的计划到达车未推算14∶30-20∶00时间段内的计划出发车较为合理. 如下表 1和表 2为到发列车数据.
设定精英解集合基数E为15,初始失败次数rfl为120,失败次数增长率rgf为1.15,其中第1层求解时间为60 s,第2层和第3层求解时间均为30 s. 在Inter Core i3-2310M 2.1 GHz & DRAM 2 G & Windows XP环境下的PC机上Java编程实现并测试. 如图 1所示为DWALMCuS模型每层的求解过程,最后得优化的到发车作业排程情况和配流方案如表 3~5所示,总的求解时间为68.7 s.
股道 优先级 编组内容
BZ07 16 015/29,071/3,072/16
BZ08 16 002/16,003/17,009/28
BZ09 16 028/67,C/1
BZ11 16 002/12,028/12
BZ12 16 015/26,071/1
BZ13 16 005/38,028/15
BZ15 16 011/12
BZ20 16 029/2,021/46,011/4
BZ21 16 011/24,012/2,002/4,033/1
BZ22 16 005/1,072/1,027/1,015/2,C/1
BZ25 16 021/23
BZ26 16 029/39,021/19
BZ27 16 039/10,033/13,034/13
BZ29 16 011/7,P/8
BZ31 16 014/23,C/18
BZ32 16 033/3,011/3,034/1,014/4
车次 优先级 到达时间 编组内容
40090 15 12∶04 009/11,014/18,024/11,C/9
40094 14 12∶21 029/16,009/9,011/40
32124 13 12∶33 032/2,034/39,033/16,C/1
40281 12 12∶45 046/4,003/1,040/1,C/1,012/2
32128 11 12∶53 C/32,009/2,041/4,016/23
47667 10 13∶06 001/7,C/21
32116 9 13∶15 039/1,005/1,C/18,046/1,034/35,040/1,036/3
32118 8 13∶25 C/61,023/3,041/2
47416 7 13∶45 034/24,005/1,C/13,015/1,021/5
32114 6 13∶55 031/3,005/45,C/14,030/2
32112 5 14∶06 C/33,041/2,016/16,033/7,009/6
42644 4 14∶16 024/1,011/19
30005 3 14∶31 C/44,035/2,015/3,030/1,016/1
40084 2 14∶43 C/4,031/2,005/10,042/8,034/16
31320 1 14∶55 005/7,009/15,C/34,036/3,030/1
车次 发车时间 优先级 满轴车数 编组方向
40081 14∶42 20 62 021,029
20304 15∶24 19 60 002,003,009
12203 15∶48 18 50 014,015
40083 16∶09 17 62 021,029
30004 16∶22 16 50 005
12201 16∶31 15 50 014,015
21002 16∶52 14 62 033,034,036,039,040,046
11507 17∶10 13 57 C
32101 17∶19 12 57 028
42641 17∶38 11 50 011,012
车次 发车时间 优先级 满轴车数 编组方向
21004 17∶53 10 62 033,034,036,039,040,046
21501 18∶15 9 62 008,024,071,072,075
21006 18∶32 8 62 033,034,036,039,040,046
30002 18∶42 7 50 005
11509 19∶02 6 57 C
42643 19∶17 5 50 011,012
11503 19∶27 4 57 C
11505 19∶36 3 57 C
11501 19∶44 2 57 C
20302 19∶52 1 60 002,003,009 
图 1 DWALMCuS模型最优解求解过程Fig. 1 The process of solving optimal solutions for the DWALMCuS model
车次 解体起止 占用股道起止 到达顺序 解体顺序
40090 13∶04-13∶34 12∶04-13∶34 1 1
40094 13∶21-13∶51 12∶21-13∶51 2 2
32124 13∶34-14∶06 12∶33-14∶06 3 3
40281 13∶51-14∶21 12∶45-14∶21 4 4
32128 14∶06-14∶36 12∶53-14∶36 5 5
47667 14∶51-15∶21 13∶06-15∶21 8 6
32116 14∶21-14∶51 13∶15-14∶51 6 7
32118 14∶36-15∶06 13∶25-15∶06 7 8
47416 15∶06-15∶36 13∶45-15∶06 9 9
32114 15∶21-15∶51 13∶55-15∶51 10 10
32112 16∶06-16∶40 14∶06-16∶40 13 11
42644 15∶36-16∶06 14∶16-16∶06 11 12
30005 16∶40-17∶10 14∶31-17∶10 15 13
40084 16∶25-16∶55 14∶43-16∶55 14 14
31320 15∶55-16∶25 14∶55-16∶25 12 15
| 车次 | 编组起止 | 占用股道起止 | 编组顺序 | 出发顺序 |
| 40081 | 12∶00-13∶00 | 13∶00-14∶42 | 1 | 1 |
| 20304 | 12∶00-13∶00 | 13∶00-15∶24 | 1 | 2 |
| 12203 | 12∶00-13∶00 | 13∶00-15∶48 | 1 | 3 |
| 40083 | 13∶00-14∶00 | 14∶00-16∶09 | 2 | 4 |
| 30004 | - | - | - | - |
| 12201 | 14∶00-15∶00 | 15∶00-16∶31 | 3 | 5 |
| 21002 | 14∶06-15∶06 | 15∶06-16∶52 | 4 | 6 |
| 11507 | 14∶36-15∶36 | 15∶36-17∶10 | 5 | 7 |
| 32101 | 13∶00-14∶00 | 14∶00-17∶19 | 2 | 8 |
| 42641 | 13∶00-14∶00 | 14∶00-17∶38 | 2 | 9 |
| 21004 | 15∶00-16∶00 | 16∶00-17∶53 | 6 | 10 |
| 21501 | - | - | - | - |
| 21006 | 17∶00-18∶00 | 18∶00-18∶32 | 11 | 11 |
| 30002 | 16∶00-17∶00 | 17∶00-18∶42 | 8 | 12 |
| 11509 | 15∶40-16∶40 | 16∶40-19∶02 | 7 | 13 |
| 42643 | 16∶06-17∶06 | 17∶06-19∶17 | 9 | 14 |
| 11503 | 17∶06-18∶06 | 18∶06-19∶27 | 12 | 15 |
| 11505 | 17∶06-18∶06 | 18∶06-19∶36 | 12 | 16 |
| 11501 | 17∶40-18∶40 | 18∶40-19∶44 | 13 | 17 |
| 20302 | 16∶40-17∶40 | 17∶40-19∶52 | 10 | 18 |
通过图 1和表 4可得在满足所有约束的前提下,各目标达到了最优. 由表 1得到方向为“005”的到达车流分布为: 32114有45辆、 40084有1辆、 31320有7辆. 这3列到达列车最早解体完毕时间分别为15∶25、 15∶13和15∶25,都比30004最晚开始编组时刻14∶52要晚,不满足车流接续约束,故30004配流不成功. 方向为“008、 024、 071、 072、 075”的到达车流总数为34辆小于62,不满足满轴约束,故21501配流不成功.
| 车次 | 车流来源: 车次(股道码)/方向(车种)/辆数 |
| 40081 | BZ20/029/2,BZ20/021/28,BZ25/021/13,BZ26/021/19 |
| 20304 | BZ08/002/16,BZ08/003/17,BZ08/009/27 |
| 12203 | BZ07/015/29,BZ12/015/20,BZ22/015/1 |
| 40083 | BZ25/021/4,BZ26/029/39,BZ26/021/19 |
| 30004 | 配流未成功 |
| 12201 | BZ12/015/6,BZ22/015/1,BZ31/014/23,BZ32/014/4,40090/014/16 |
| 21002 | BZ21/033/1,BZ27/039/10,BZ27/033/13,BZ27/034/13,BZ32/033/3,BZ32/034/1,32124/034/21 |
| 11507 | BZ09/C/1,BZ22/C/1,BZ31/C/18,40090/C/9,32124/C/1,32128/C/27 |
| 32101 | BZ09/028/30,BZ11/028/12,BZ13/028/15 |
| 42641 | BZ15/011/12,BZ20/011/4,BZ21/011/24,BZ21/012/2,BZ29/011/7,BZ32/011/1 |
| 21004 | 32124/034/18,32124/033/16,32116/039/1,32116/046/1,32116/034/26 |
| 21501 | 配流未成功 |
| 21006 | 32116/034/9,32116/040/1,32116/036/3,47416/034/24,32112/033/7,40084/034/16,31320/036/2 |
| 30002 | BZ13/005/38,BZ22/005/1,32116/005/1,47416/005/1,32114/005/9 |
| 11509 | 32128/C/5,47667/C/21,32116/C/18,47416/C/13 |
| 42643 | BZ32/011/2,40094/011/40,42644/011/8 |
| 11503 | 32114/C/14,32112/C/33,40084/C/4,31320/C/6 |
| 11505 | 40281/C/1,32118/C/56 |
| 11501 | 32118/C/5,30005/C/44,31320/C/8 |
| 20302 | BZ08/009/1,BZ11/002/12,BZ21/002/4,40090/009/11,40094/009/9,40281/003/1,32128/009/2,32112/009/6,31320/009/14 |
由表 3得到先到的到达车未必先解体. 这是为了能够多发车,必须使得车流接续紧张的到达车优先解体,所以到发车解编顺序是最优的.
4.3 算法比较与分析4.3.1 与其它算法比较
以3个目标最优值及总的求解时间t为指标,本研究IAIS-CPr-MPCS算法分别与使用深度优先标准回溯算法IAIS-CPr-DFS、 随机重启算法IAIS-CPr-RS和不带初始解的迭代算法IAISNIS-CPr-MPCS相比较,从表 6可知本算法比其它算法效率要高,且求解质量优于算法IAIS-CPr-DFS.
| 算法 | f1 | f2 | f3 | t | 比较f1 | 比较时间 |
| IAIS-CPr-MPCS | 185 | 120 | 6 806 | 58.9 | - | - |
| IAIS-CPr-DFS | 25 | 3 | 896 | 600.0 | -86.49% | -918.68% |
| IAIS-CPr-RS | 185 | 120 | 6 806 | 392.4 | - | -566.21% |
| IAISNIS-CPr-MPCS | 185 | 120 | 6 806 | 128.4 | - | -118.00% |
1) 精英解集合基数E对算法性能影响
解的质量、 求解时间和空间成本与E成正相关. 假设其它参数不变,如下图 2所示为f1的最优值、 求解时间与E之间的关系. 当E<15,求解时间较短,解的质量不高,但是解的值是逐渐递增的; 当E>15,解的质量不变,但是求解时间增加,所以E取15.
 |
| 图 2 精英解数目与算法性能关系Fig. 2 The relationship between the number of the elite solutions and the algorithm performance |
2) search(e,b)算法失败界限对算法性能影响
假设其它参数不变,search(e,b)初始失败次数上界rfl与f1最优值、 求解时间之间的关系如图 3所示.
 |
| 图 3 初始失败次数上界与算法性能关系Fig. 3 The relationship between initial upper bound of the number of failures and the algorithm performance |
由图 3可知,增加rfl并不能提高求解效率和增加解的质量,虽然增加rfl可以提高每轮精英解的质量,减少了重启次数,但是增加了每轮的迭代次数; 当失败次数较少时,重启次数会增多,故不会影响解的质量,本文取使得求解时间最短的rfl值为120. 同样得到失败次数增长率rgf与算法性能的关系.
5 结论本文综合考虑了到发车流的不均衡、 不同解体模式模型下的通用性和阶段计划滚动编制特点等,基于CP和LMO理论建立了编组站动态字典序累积调度模型,并设计约束传播和多点构建性搜索的混合迭代算法,解决了在实际应用中模型和算法的扩展性、 稳定性和求解效率等问题. 在此基础上,再研究直通车接入股道、 配流剩余到解车接入股道与解体、 调车场股道活用、 阶段计划调整等问题与动态配流的综合优化,就可以实现编组站阶段计划的智能编制.
| [1] | 王正彬, 杜文, 吴柏青, 等. 基于解编顺序的阶段计划车流推算模型及算法[J]. 铁道学报, 2008, 43(1): 91-95. Wang Z B, Du W, Wu B Q, et al. Model and algorithm for estimation of wagon flow of stage operating plan based on break-up and make-up sequences[J]. Journal of the China Railway Society, 2008, 43(1): 91-95. . |
| [2] | 申永生, 何世伟, 王保华. 免疫算法求解编组站阶段计划配流问题研究[J]. 铁道学报, 2009, 31(4): 1-6. Shen Y S, He S W, Wang B H, et al. Study on allocation of wagon-flow in phase plan by using immune algorithm[J]. . Journal of the China Railway Society, 2009, 31(4): 1-6. |
| [3] | 赵军, 彭其渊, 文超, 等. 技术站广义动态配流问题的遗传算法[J]. 铁道学报, 2010, 32(3): 9-15. Zhao J, Peng Q Y, Wen C, et al. Genetic algorithm for solution to generalized dynamic wagon-flow allocation problem with technical railway stations[J]. Journal of the China Railway Society, 2010, 32(3): 9-15. . |
| [4] | 赵军, 彭其渊, 文超, 等. 技术站广义动态配流问题的局部邻域搜索算法[J]. 西南交通大学学报, 2010, 45(3): 486-492. Zhao J, Peng Q Y, Wen C, et al. Local neighborhood search algorithm for generalized dynamic wagon-flow allocation of railway technical stations[J]. Journal of Southwest Jiaotong University, 2010, 45(3): 486-492.. |
| [5] | 赵军, 韩雪松, 彭其渊. 技术站配流与调机运用综合问题的拉格朗日松弛算法[J]. 铁道学报, 2011, 33(11): 1-7. Zhao J, Han X S, Peng Q Y. Lagrangian relaxation algorithm for integrated wagon-flow allocation and shunting locomotive scheduling at technical railway station[J]. Journal of the China Railway Society, 2011, 33(11): 1-7.. |
| [6] | 赵军, 彭其渊. 单向编组站配流与调机运用综合问题[J]. 铁道学报, 2012, 34(11): 1-9. Zhao J, Peng Q Y. Integrated wagon-flow allocation and shunting locomotive scheduling problem at single-directional marshalling station[J]. Journal of the China Railway Society, 2012, 34(11): 1-9. . |
| [7] | 薛锋, 陈崇双, 户佐安. 铁路编组站配流与调机运用的协调决策优化[J]. 计算机工程与应用, 2013, 49(5): 32-35. Xue F, Chen C S, Hu Z A. Coordination decision optimization for wagon-flow allocating and shunting locomotive utilization in railway marshalling station[J]. Computer Engineering and Applications, 2013, 49(5): 32-35.. |
| [8] | 薛锋. 铁路编组站配流协同优化模型与算法[J]. 系统工程理论与实践, 2013, 33(11): 2930-2936. Xue F. Collaborative optimization model and algorithm for wagon-flow allocation in railway marshalling station[J]. Systems Engineering: Theory & Practice, 2013, 33(11): 2930-2936. . |
| [9] | 黎浩东, 宋瑞, 何世伟, 等. 基于列车解编作业时间估算的编组站阶段计划配流优化[J]. 中南大学学报: 自然科学版, 2014, 45(1): 317-327. Li H D, Song R, He S W, et al. Wagon-flow allocation of stage plan for marshaling station based on time estimation of breakup and makeup of trains[J]. Journal of Central South University: Science and Technology, 2014, 45(1): 317-327. . |
| [10] | 刘露. 基于约束传播技术的资源受限项目调度问题求解算法[D]. 沈阳: 东北大学, 2011: 10-30. Liu L. Constraint propagation based algorithms for solving resource-constrained project scheduling problems[D].. Shenyang: Northeastern University, 2011: 10-30. |
| [11] | 刘士新, 宋健海. 求解资源受限项目调度问题的约束规划/数学规划混合算法[J]. 控制理论与应用, 2011, 28(8): 1113-1120. Liu S X, Song J H. Combination of constraint programming and mathematical programming for solving resources-constrained project-scheduling problems[J]. Control Theory & Applications, 2011, 28(8): 1113-1120. . |
| [12] | 刘士新, 郭哲, 唐加福. 具有优先关系的累积调度问题的约束传播算法[J]. 自动化学报, 2010, 36(4): 603-609. Liu S X, Guo Z, Tang J F. Constraint propagation for cumulative scheduling problems with precedences[J]. Aata Automatica Sinica, 2010, 36(4): 603-609. . |
| [13] | Rossi F, van Beek P, Walsh T. Handbook of constraint programming[M]. Amsterdam, Holland: Elsevier, 2006: 27-78, 206-235, 541-580, 778-781. |
| [14] | 马亮, 郭进, 陈光伟. 基于约束程序累积调度的编组站静态配流模型研究[J]. 铁道学报, 2014, 36(1): 8-15. Ma L, Guo J, Chen G W. Study on static wagon-Flow allocation model based on constraint programming cumulative scheduling in a marshalling station[J]. Journal of the China Railway Society, 2014, 36(1): 8-15. . |
| [15] | Ojha A K, Biswal K K. Lexicographic multi-objective geometric programming problems[J]. IJCSI International Journal of Computer Science Issues, 2009, 6(2): 20-24. |
| [16] | Beck J C. Solution-guided multi-point constructive search for job shop scheduling[J]. Journal of Artificial Intelligence Research, 2007, 29: 49-77. |



