1 引言
柔性作业车间调度问题(flexible job-shop scheduling problem,FJSP)是作业车间调度问题(job-shop scheduling problem,JSP)的扩展,它突破了JSP中的机床限制,各工序可在多台可选机床上加工,更符合实际的生产情况. Brucker和Schile在文[1]中首次提出了FJSP的概念,并给出了求解简单FJSP(只包含两个工件)的多项式算法. 但随着问题规模逐渐增大,计算量会出现“指数爆炸”现象,业已证明该问题属于NP难题,至今还没有一种算法能够全面而有效地对其进行求解. 迄今为止,提出了各种各样的算法对其进行求解,以期找出更好的算法. 文[2]用拉格朗日松弛法(Lagrangian relaxation)对其进行求解,并与基于知识的调度进行比较,说明所提出算法的优越性. 文[3]用混合整数规划(mixed integer programming)对其进行求解,考虑了该问题的最小化提前/延后目标,并说明了该方法在某些情况下(大约9个工件、 3个机器)能够得到最优调度解并可以应用于实际生产中. 文[4]用基于规则的启发式算法求解该问题,并说明了所提出的方法能够快速地得到满意解. 还有一些智能算法也用于了求解FJSP问题,如文[5]用禁忌搜索算法(TS)求解、 文[6, 7]用遗传算法(GA)求解、 文[8]用粒子群算法(PSO)求解等. 为了探索求解FJSP的更多途径,在基本入侵杂草优化算法原理的基础上,提出一种离散多种群入侵杂草优化算法(invasive weed optimization algorithm with discrete multi-population,IWODMP).
入侵杂草优化算法(IWO)是由Mehrabian等于2006年在文[9]中提出,该算法是一种模拟自然界杂草殖民过程的随机搜索算法,具有鲁棒性强、 易于理解和易于实现等特点. 该算法提出后,吸引了大量的学者对其进行研究. 如,Hajimirsadeghi和Lucas在文[10]提出一种IWO与PSO的融合算法(IWOPSO),该算法在杂草繁殖种子后对其进行速度和位移的更新,然后进行正态空间扩散,达到了避免算法陷入局部最优的目的. Ahmadi和Mojallali在文[11]中利用混沌搜索的特点对其进行改进,提出了一种混沌入侵杂草优化算法. Nayak等在文[12]中提出了一种自适应的IWO算法,提高了算法的初期全局探索能力和后期挖掘能力. 文[13, 14, 15]已分别将IWO成功应用到天线阵列设计、 DNA序列计算、 压电激励器放置等领域. 但很少有文献提到利用IWO求解FJSP问题. 本文提出的IWODMP算法是在基本IWO算法的基础上引入交叉算子和多种群思想,且在算法初期种群间不进行交流,根据组合优化的特点将其离散化,采用自适应变异位数和邻域搜索策略进行空间扩展. 并将IWODMP算法用于求解FJSP问题,通过实例验证了所提出算法的有效性和优越性.
2 柔性作业车间调度问题描述柔性作业车间调度是比车间调度更复杂的组合优化难题,而且也更符合现代多品种、 小批量的生产模式. 柔性作业车间调度又分为部分柔性作业车间调度和全部柔性作业车间调度. 如果存在至少一个工序不能在全部机床上加工,则为部分柔性作业车间调度; 反之,则为全部柔性作业车间调度. 现将柔性作业车间调度问题描述如下: n个工件(J1,J2,…,Jn)在m台机床(M1,M2,…,Mm)上加工,工件Ji有ni道工序(oi1,oi2,…,oini). 工件Ji的第j道工序oij在机床Mk上的加工时间Pijk可以不同. 同一道工序可以选择不同的机床进行加工且加工时间一般不同,同一机床在同一时间只能加工一道工序,同一工序同一时间只能在一台机器上加工,且该道工序一旦开始加工就不能中断,直到该道工序加工完成. 同一工件的不同工序之间有先后关系,同一机床上加工的不同工序间在满足前述先后关系的情况下没有先后关系. 调度过程就是合理安排所有工序到合适的机床上,使得一个或多个给定的目标最优. 常用的目标函数有最大完工时间最小、 机床最大负荷最小、 总机床负荷最小、 提前/拖期最小等. 本文采用其中的正规性能指标——最大完工时间最小、 机床最大负荷最小、 总床负荷最小——作为目标函数,如式(1)~(3)所示:

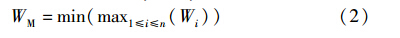
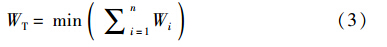
其中,CM、 WM、 WT分别表示最大完工时间、 机床最大负荷、 总机床负荷; Cj表示该工件的最后一道工序的完工时间; Wi是该机器上的加工时间总和.
表 1为2个工件5道工序5台机器的加工实例(2×5实例).
| 工件 | 工序 | ||||
| 可以选择加工的机器 | |||||
| M1 | M2 | M3 | M4 | M5 | |
| J1 | |||||
| J2 | |||||
| o11 | 2 | 6 | 5 | 3 | 4 |
| o12 | — | 8 | — | 4 | — |
| o21 | 3 | — | 6 | — | 5 |
| o22 | 4 | 6 | 5 | — | — |
| o23 | — | 7 | 11 | 5 | 8 |
注: “—”表示该工序不能在该机床上加工; 表中数字表示该工序在该机器上的加工时间.
3.1 基本IWO算法原理
IWO算法是模拟稻田杂草殖民过程的一种随机搜索算法,把稻田比喻成问题的解空间,杂草比喻成问题的可行解. 种群是所有杂草的集合,在进化过程中,杂草根据自身适应度的好坏产生种子,适应度好的产生的种子数多,适应度坏的产生的种子数少. 产生的种子在杂草周围按正态分布的步长生长成杂草,初期步长大,后期步长小,杂草和种子一起作为待研究的对象. 若达到给定的最大种群数目pmax,则对种群按适应度排序,选择适应度好的杂草,保持种群大小; 否则,继续产生种子,直到达到给定的最大种群数目pmax.
3.2 IWODMP算法IWODMP是在基本IWO算法原理的基础上提出的. 该算法引入多种群思想,并在算法初期保持种群的独立性,在各自种群内部独立搜索,以期算法初期独立地在各自种群内搜索,即对解空间进行大范围搜索. 为了保留优秀基因,进行种群内部交流,降低算法前期由于空间扩展步长过大而跳过最优解的概率,增强算法的稳定性,引入遗传算法的交叉算子. 在算法后期,为了共享各个种群内部的优秀杂草和提高算法的后期收敛速度,通过比较每个种群中最优的杂草,找出最好的一个杂草,加入到其余种群中进行种群间交流.
当空间扩展时,考虑到组合优化问题的特点,编码后的杂草与杂草之间空间关系复杂,杂草与杂草之间的距离不便于计算,将基本IWO算法在空间扩展时的“产生的种子在杂草周围按正态分布的步长生长成杂草”变为根据迭代次数自适应地改变变异位数的策略,以适应组合优化的特点. 在算法初期变异位数较多,空间扩展步长大,增强了算法的全局搜索性能; 在算法后期,随着变异位数的减少,空间扩展步长减小,提高了算法的局部挖掘能力. 当选择杂草进入下一代时,引入领域搜索策略,根据变异位数和种子数产生2倍于种子数的种子,选择适应度好的种子进入下一代,进一步提高算法的局部搜索能力.
3.3 IWODMP算法的步骤步骤1 随机初始化杂草,分为杂草数相等的P个种群(实践表明2≤P≤5算法性能较好),每个种群的初始杂草个数为pmin,最大杂草个数为pmax.
步骤2 判断是否达到最大迭代次数,若是则输出结果,退出程序; 若否,则转步骤3.
步骤3 进行各个种群内交流并保留精英杂草,计算各个杂草的适应度,根据式(4)计算各个杂草的种子数目. 根据式(5)和式(6)计算空间扩展所要变异的基因位数d(当Niter≤2×Niterm/3时用式(5),当Niter>2×Niterm/3时用式(6)),再根据给定的领域函数选择种子数目个杂草,进入下一代:
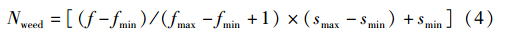
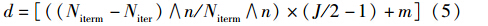
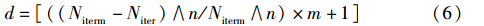
式中,Nweed表示当前杂草欲产生的种子数; f、 fmin、 fmax分别表示当前杂草的适应度、 当代最小适应度和最大适应度; smax、 smin分别表示各杂草能产生的最大种子数和最小种子数; “[]”表示取整; d表示需要变异的位数; Niterm表示最大迭代次数; Niter表示当前迭代次数; J表示杂草的基因位数总数; n和m的不同可以控制变异位数之间的差距. n越大差距越大,空间搜索范围缩小越快,可根据实际程序运行取值(本文n=4,有较好的范围缩小速度); m的作用是控制种群交流以后的变异位数,为了让算法收敛速度加快,在算法后期种群交流以后,变异位数变得很小,以期望算法在杂草周围作小范围的搜索,所以m通常取较小的整数(本文m=3).
步骤4 判断杂草数目是否大于最大杂草数. 若是,则转到步骤5; 否则转到步骤2.
步骤5 对各个种群内杂草进行排序选择,保持种群大小.
步骤6 判断是否达到种群交流的迭代次数(本文在2×Niterm/3代以后交流): 若是,则转到步骤7; 否则,转到步骤2.
步骤7 进行种群交流,选择P个种群中最好的杂草加入到每个种群,转步骤2.
3.4 IWODMP算法中FJSP杂草的编码与解码杂草编码时,采用文[16]提出的分段编码MSOS. 机器编码部分: 基因位表示工序,基因位上的数字表示该工序可以选择的机器集合中的第几台机器. 如表 1所示实例的一个机器编码[1 2 1 1 1],第1个基因位上的数字1表示工序o11选择第1台可以选择的机器(M1),第2个基因位上的数字2表示工序o12选择第2台可以选择的机器(M4),以此类推. 工序编码部分: 基因位置表示工序,基因位上的数表示工件号. 如表 1实例的一个工序编码为[2 2 1 1 2],第2个2表示此时加工工件J2的第2道工序(o22),以此类推.
解码时,本文在文[16]的基础上提出矩阵解码法. 该方法分2步: 第1步,解码成矩阵M1(M1法); 第2步,由M1解码成矩阵M2(M2法).
M1法: 由于编码是分段编码的,M1法解码也需分段解码,以表 1实例的杂草[1 2 1 1 1 2 2 1 1 2]为例. 首先,进行机器解码,机器部分的编码是[1 2 1 1 1],对照表 1进行解码,解码成机器编号向量Jm=[1 4 1 1 2],其中基因位表示工序,基因位上的数字表示机器编号,如第2个基因位上的数字4表示该工序(o12)选择机器M4; 其次,进行工序解码,解码成加工时间向量Jtime=[2 4 3 4 7],其中基因位表示工序,基因位上的数字表示该工序在相应机器上的加工时间,如第2个基因位上的数字4表示工序o12在机器M4上的加工时间为4; 最后,将Jm、 Jtime合并,并联系工件和工序信息,解码成矩阵M1. 表 1实例解码后的M1如下所示:
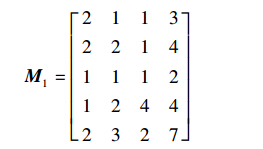
M2法: 根据矩阵M1计算每道工序的开始加工时间点和结束加工时间点,具体方法如下: (1) 初始化矩阵M2,其中前4列与M1相同,第5、 6列初始化为0,分别表示该工序的开始加工时间点和结束加工时间点. (2) 读取矩阵M1的第1行,第1行表示的工序是该工件的第1道工序(o21),也是该机器(M1)的第1道也是唯一一道工序,所以该行工序在该机器上的开始加工时间点sijk(sijk表示工件i的第j道工序在机器k上的开始加工时间点)为0,结束加工时间点fijk=sijk+pijk=pijk(pijk表示工件i的第j道工序在机器k上的加工时间),依次将其赋值到矩阵M2的第5、 6列. (3) 读取矩阵M1的第l行,判断该行第1、 2列的数字所表示的工序(oij)在该工件(Ji)的工序位置情况和该工序选择的机器上已安排工序情况: 若工序oij是工件Ji的第1道工序且所选择的机器上没有安排其它工序,则该工序可以从0时刻开始加工,sijk=0,fijk=sijk+pijk,依次将其赋值到矩阵M2的第5、 6列; 若工序oij是工件Ji的第1道工序且所选择的机器上安排有其它工序,则找出该机器上所有的空闲时间段[si,ei],依次判断ei-si与Pijk的关系,选择第1次使Pijk≤ei-si的时间段[si,ei]的开始时间点(si),sijk=si,fijk=sijk+pijk,依次将其赋值到矩阵M2的第5、 6列; 若工序oij不是工件Ji的第1道工序且所选择的机器上没有安排其它工序,则该工序oij可以从它的上一道工序oij-1的结束加工时间点(fij-1k)开始加工,sijk=fij-1k,fijk=sijk+pijk,依次将其赋值到矩阵M2的第5、 6列; 若工序oij不是工件Ji的第1道工序且所选择的机器上安排有其它工序,则找出该机器上所有的空闲时间段[si,ei],依次判断ei-si与pijk的关系、 fij-1k与si的关系: 若pijk≥ei-si且fij-1k≤si,则sijk=si,fijk=sijk+pijk,依次将其赋值到矩阵M2的第5、 6列; 若pijk≥ei-si且fij-1k>si,则判断ei-fij-1k是否大于或者等于pijk: 若是,则sijk=fij-1k、 fijk=sijk+pijk,依次将其赋值到矩阵M2的第5、 6列; 若否则按上述方法判断下一个空闲时间段. (4) 判断矩阵M1是否读取完毕: 若否,则重复步骤(3); 若是,则输出矩阵M2. 表 1所示例子的M2矩阵如下所示:

通过上述矩阵解码法得到矩阵M2,由矩阵M2就可以画出相应的甘特图. 该矩阵解码法保证了解码成活动调度,由调度理论知,活动调度中一定包含最优调度. 该矩阵解码法容易理解且易于编程实现.
3.5 IWODMP算法中FJSP杂草交叉与空间扩展由于杂草编码采用分段编码,交叉也需分段交叉. 机器编码部分的交叉采用均匀交叉,具体方法如下: 随机生成一个1到J的整数a,随机生成a个1到J的整数,将两父代a个位置上的基因进行交换,得到子代. 工序编码部分的交叉采用文[17]提出的POX交叉方法: 随机将工件分成部分1和部分2,将父代1/父代2属于部分1/部分2的基因复制到子代1/子代2上,并保留其位置; 将父代2/父代1不属于部分1/部分2复制到子代1/子代2上,并保留其顺序.
空间扩展时,对杂草也进行分段处理. 机器编码部分: 根据适应度计算出需要变异的杂草基因位数d,随机生成一个1到J的随机整数,所产生的整数代表需要变异的基因位置,在该位置上随机生成一个1到Mik的整数(Mik表示工件Ji可以选择的机器数),替换到该位置上,重复d次,得到一个种子; 按照给定的领域函数对该种子进行处理,给出2倍于种子数目的杂草,选出Nweed个适应度较好的种子,完成机器变异. 工序编码部分: 进行d次随机交换基因位上的数字,给出2倍于种子数目的种子,选出Nweed个适应度好的种子,进入下一代.
4 仿真结果与分析为了比较算法的性能,采用与Nasr等[18]、 Kacem等[19]、 Zhang等[20]相同的数据进行测试. 这些有4×6小规模的部分柔性作业车间调度问题,有8×8和10×10较大规模的部分柔性和全部柔性的问题. 这3个例子在文献中出现的次数较多,可以用于比较的数据也较多; 此外,这3个例子代表了部分柔性和全部柔性,从小规模到较大规模的柔性作业车间问题,便于比较,因此选择了这3个例子作为例证.
上述算法采用Matlab 7.0编程实现,运行环境为: Win7 32位操作系统,i5-2450M CPU,内存为2G. IWODMP算法主要参数为: 种群数P=3,每个种群的初始杂草个数pmin=10,pmax=30,smin=1,smax=5,式(5)中的n=4,m=3,终止代数为300,每个实例独立运行10次.
表 2给出了4×6实例的测试比较结果(表中数据除了本文算法的结果,其余数据均是直接引用原文数据),由表 2中数据可以看出: 最大完工时间小于文[18]给出的18,并且平均收敛率为100%,说明算法稳定,性能优越. 图 1给出了相应的甘特图.
 |
| 图 1 4×6实例(CM=17)的甘特图Fig. 1 The Gantt chart of 4×6 FJSP (CM=17) |
表 3给出了8×8实例和10×10实例的测试比较结果(表中数据除了本文算法的结果,其余数据均是直接引用原文数据). 由表 3数据可以看出: 最大完工时间最小、 机床最大负荷最小、 总机床负荷最小的最优值都小于或等于其它文献给出的数据,平均值全部小于其它文献给出的数据,说明算法稳定,性能优越. 而且8×8实例的机器总负荷最小为73,小于Kacem等[19]的75和张国辉等[21]给出的77,说明了算法的优越性.
图 2给出了8×8实例的最大完工时间(CM=14)的甘特图. 图 3、 4分别给出了10×10实例的最大完工时间(CM=7)的算法搜索过程和相应的甘特图. 图 5给出了机器总负荷(CM=73)的甘特图.
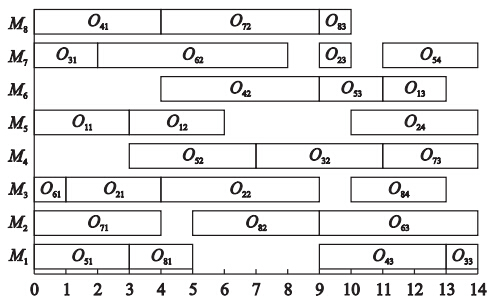 |
| 图 2 8×8实例(CM=14)的甘特图Fig. 2 The Gantt chart of 8×8 FJSP (CM=14) |
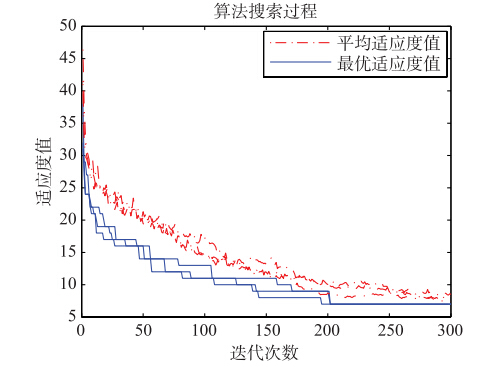 |
| 图 3 10×10实例(CM=7)的搜索过程Fig. 3 The searchprocess of 10×10 FJSP (CM=7) |
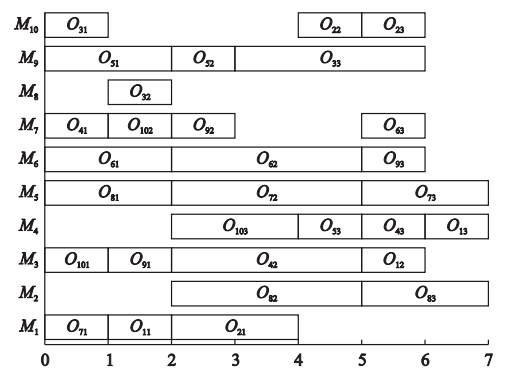 |
| 图 4 10×10实例(CM=7)的甘特图Fig. 4 The Gantt chart of 10×10 FJSP (CM=7) |
 |
| 图 5 10×10实例(WT=73)的甘特图Fig. 5 The Gantt chart of 10×10 FJSP (WT=73) |
5 结论
本文研究了柔性作业车间调度问题的不同性能指标(最大完工时间最小、 机床最大负荷最小、 总机床负荷最小). 从数据看出,各指标平均值均小于其它文献的数据,证明了所提出的离散多种群入侵杂草优化算法的有效性和优越性. 在解码时,给出了一种矩阵解码法,使之解码成活动调度,由调度理论可知,保证了不会漏掉最优解,且该矩阵解码法容易理解和易于编程实现.
此外,入侵杂草优化算法数学理论基础薄弱,在提出的离散多种群入侵优化算法中,可控参数较多,多是根据反复运行程序得出,缺少选择各参数的理论指导,值得进一步研究.
| [1] | Brucker P, Schlie R. Job-shop scheduling with multi-purpose machines[J]. Computing, 1990, 45(4): 369-375. |
| [2] | Hoitomt D J, Luh P B, Pattipati K R. A practical approach to job-shop scheduling problems[J]. IEEE Transactions on Robotics and Automation, 1993, 9(1): 1-13. |
| [3] | Zhu Z W, Heady R B. Minimizing the sum of earliness/tardiness in multi-machine scheduling: A mixed integerprogramming approach[J]. Computers & Industrial Engineering, 2000, 38(2): 297-305. |
| [4] | Montazeri M, Van Wassenhove L N. Analysis of scheduling rules for an FMS[J]. International Journal of Production Research, 1990, 28(4): 785-802. |
| [5] | Mastrolilli M, Gambardella L M. Effective neighbourhood functions for the flexible job shop problem[J]. Journal of Scheduling, 2000, 3(1): 3-20. |
| [6] | 杨晓梅, 曾建潮. 遗传算法求解柔性Job shop调度问题[J]. 控制与决策, 2004, 19(10): 1197-1200. Yang X M, Zeng J C. Solving flexible job shop scheduling problem using genetic algorithm[J]. Control and Decision, 2004, 19(10): 1197-1200. . |
| [7] | 张维存, 郑王愕, 吴晓丹. 基于主—从遗传算法求解柔性调度问题[J]. 计算机集成制造系统, 2006, 12(1): 1241-1245. Zhang W C, Zheng W E, Wu X D. Solving flexible job-shop scheduling problems based on master-slavegenetic algorithm[J]. Computer Integrated Manufacturing Systems, 2006, 12(1): 1241-1245. . |
| [8] | 罗德相, 周永权, 黄华娟, 等. 多种群粒子群优化算法[J]. 计算机工程与应用, 2010, 46(19): 51-54. Luo D X, Zhou Y Q, Huang H J, et al. Multi-conolyparticle swarm optimization algorithm[J]. Computer Engineering and Applications, 2010, 46(19): 51-54. |
| [9] | Mehrabian A R, Lucas C. A novel numerical optimization algorithm inspired from weed colonization[J]. Ecological Informatics, 2006, 1(4): 355-366. |
| [10] | Hajimirsadeghi H, Lucas C. A hybrid IWO/PSO algorithm for fast and global optimization[C]//IEEE Eurocn. Piscataway, NJ, USA: IEEE, 2009: 1964-1971. |
| [11] | Ahmadi M, Mojallali H. Chaotic invasive weedoptimization algorithm with application to parameter estimation of chaotic systems[J]. Chaos, Solitons & Fractals, 2012, 45(9/10): 1108-1120. |
| [12] | Nayak M R, Krishnanand K R, Rout P K. Optimal reactive power dispatch based on adaptive invasive weed optimization algorithm[C]//International Conferenceon Energy, Automation, and Signal. 2011: 1-7. |
| [13] | Mallahzadeh A R, Oraizi H, Davoodi-Rad Z. Application of the invasive weed optimization technique for antenna configurations[J]. Progressin Electromagnetics Research: Pier, 2008, 79: 137-150. |
| [14] | Zhang X C, Wang Y F, Cui G Z, et al. Application of a novel IWO to the design of encoding sequences for DNA computing[J]. Computers and Mathematics with Applications, 2009, 57(11/12): 2001-2008. |
| [15] | Mehrabian A R, Yousefi-Koma A. A novel technique for optimal placement of piezoelectric actuators on smart structures[J]. Journal of the Franklin Institute: Engineeringand Applied Mathematics, 2011, 348(1): 12-23. |
| [16] | 高亮, 张国辉, 王晓娟. 柔性作业车间调度智能算法及应用[M]. 武汉: 华中科技大学出版社, 2012: 30-32. Gao L, Zhang G H, Wang X J. The intelligence algorithm of FJSP[M]. Wuhan: Huazhong University of Science and Technology Press, 2012: 30-32. |
| [17] | 张超勇, 饶运清, 李培根, 等. 柔性作业车间调度问题的两级遗传算法[J]. 机械工程学报, 2007, 43(4): 119-124. Zhang C Y, Rao Y Q, Li P G, et al. Bilevel genetic algorithm for the flexible job-shop scheduling problem[J]. Chinese Journal of Mechanical Engineering, 2007, 43(4): 119-124. . |
| [18] | Nasr N, Elsayed E A. Job shop scheduling with alternative machines[J]. International Journal of Production Research, 1990, 28(9): 1595-1609. |
| [19] | Kacem I, Hammadi S, Borne P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems[J]. IEEE Transactions on Systems, Man and Cybernetics: Part C, 2002, 32(1): 1-13. |
| [20] | Zhang H P, Gen M. Multistage-based genetic algorithm for flexible job-shop scheduling problem[J]. Complexity International, 2005, 11: 223-232. |
| [21] | 张国辉, 高亮, 李培根, 等. 改进遗传算法求解柔性作业车间调度问题[J]. 机械工程学报, 2009, 45(7): 145-151. Zhang G H, Gao L, Li P G, et al. Improved genetic algorithm for the flexible job-shop scheduling problem[J]. Chinese Journal of Mechanical Engineering, 2009, 45(7): 145-151. |



