2. 南京航空航天大学自动化学院, 江苏 南京 210016;
3. 东南大学自动化学院, 江苏 南京 210096
2. School of Automation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. School of Automation, Southeast University, Nanjing 210096, China
1 引言
变速变桨风力发电机由于其功率控制灵活,承受的机械载荷小等优点,已成为目前主流的商用机型和风力发电领域的研究热点[1, 2, 3, 4, 5, 6]. 针对整个风速范围内的风速变化,典型的控制策略是: 在额定风速以下,保持桨叶的桨距角为0°,通过调节发电机的电磁转矩使发电机转速迅速跟上风速变化,达到最大功率捕获的目的; 在额定风速以上,保持电磁转矩恒定,当风速变化时,通过统一调节3个叶片的桨距角改变风力机的气动转矩来维持转速恒定,实现恒功率控制[7, 8].
传统的桨距角控制方法总是假定在叶片的扫略面上风速相同,采用统一调节3个叶片桨距角的方法将导致每个桨叶在拍打方向的气动载荷较大,影响风力机的使用寿命. 如果能独立调节每个叶片的桨距角,抵消该叶片上的风速波动,将极大地减小转速波动,降低叶片所受的机械应力,提高机组寿命. 目前,独立变桨距控制策略主要有基于叶片受力分析的控制策略及基于叶片方位角变化综合作用分析的控制策略. 前者以载荷测量为基础,再根据某种控制算法进行桨距角独立控制以抑制气动载荷[9, 10],这种方法需要在叶片的多个位置安装加速度传感器,这对于大型风力机,一般是不允许的; 另一种基于方位角的桨距角控制方法是根据风切变效应和塔影效应引起风速在空间分布不均,造成风力叶片在空间内受力不均的情况,通过周期性改变各个叶片的桨距角来达到降低载荷的目的. 这种方法不需要知道载荷模型,仅需要测量叶片的方位角,而许多风力机上都安装有测速传感器,因此这种方法更能得到工程应用.
文[11, 12]设计了周期独立变桨控制器,控制器由统一变桨控制器和权系数分配独立变桨控制器组成,在叶片方位角的一个周期内通过对统一变桨信号进行权系数分配来实现独立变桨. 但这种方法是将统一变桨控制律按照风切变规律使用固定权系数进行分配,从而得到每个桨叶的独立变桨信号. 该方法对统一变桨信号的频率和幅度都非常敏感,因此当统一变桨调节的频率或幅度过大时,独立变桨的效果均不理想.
本文针对风切变情况下的风力机非线性模型,提出一种额定风速以上基于方位角的恒功率独立桨距角控制方法,其控制系统由统一变桨控制器与独立变桨控制器组成. 其中基于自抗扰控制(active disturbance rejection control,ADRC)方法的集中桨距角控制器给出风力机系统在各种风速条件下的桨距角一个粗略的调节范围,由于扩张观测器(extended state observer,ESO)能够观测系统的扰动输入和模型误差,因此对因风速变化而偏离控制器设计点所造成的模型不确定性以及由于模型参数变化而造成的不确定性具有较强的鲁棒性; 独立桨距角控制器在统一变桨信号的基础上对由风切变引起的各个叶片上的空气动力转矩分别进行补偿. 理论分析和仿真结果表明,本文独立桨距角控制方法能有效抑制叶尖拍打方向的气动载荷,独立桨距角信号受统一变桨信号的幅值和频率影响小,对参数变化、 风速变化、 电磁转矩的扰动具有较强的鲁棒性.
2 模型描述2.1 无风切变作用的风力机特性
传统风力机功率控制问题中总假设风速方向与风力机扫掠平面垂直,且在风力机的旋转平面内风速相同. 若风力机叶片采用统一变桨的方式,即3个叶片的桨距角都以相同的角度变化进行调节. 基于以上考虑的风力机机械子系统可表示为[13]
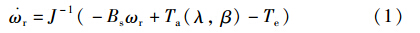
式中,ωr为风力机转速; J与Bs是风力机的惯性常数与阻尼系数; Ta与Te分别为空气动力转矩与电磁转矩,满足以下关系:


式中,ρ是空气密度,λ表示叶尖速比,r和v分别为风力机叶片半径以及风力机扫掠面的平均风速,Cq为风力机转矩系数,β表示叶片的桨距角.
额定风速以上,要通过减小风能的吸收来保证上网功率的平衡,即减小风力机的空气动力转矩Ta. 从式(2)可看到,空气动力转矩与叶尖速比和叶片的桨距角有关. 定桨风力机由于桨叶桨距角固定,要减小Ta,只能靠失速调节增大叶尖速比,使得风力机进入失速区来减小风能的吸收. 而对于变桨风力机,由于桨叶桨距角可调节,有些风力机甚至可分别调节每个桨叶的桨距角,因此通过调节桨距角改变Ta则成为额定风速以上变桨风力机普遍使用的控制方法.
2.2 风切变模型在大气边界层中,平均风速随高度的上升而增加,其变化称为风切变或风速廓线,一般服从指数分布或Prandtl对数分布[14]. 研究表明,用指数律公式计算的风速值与实测值的偏差比用对数律计算的风速值与实测、 值的偏差要小,并且随着高度的增加,用对数律公式计算的风速值与实测值的偏差增大,我国在进行风资源评估时也常采用指数律分布[15]:

式中,v0表示离地高度H0处风力机中心的风速; vH表示风力机上离地H处的风速; κ是风切变指数,其数值与地表粗糙度常数有关,在我国的很多区域,按经验可取0.143作为近似值.
在风切变的影响下,第i个桨叶离风力机中心r/m处所受的风速满足式(5)的分布:
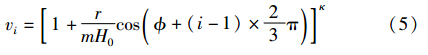
式中m>0为比例系数, 为风力机方位角,即为风力机叶片沿顺时针方向偏离塔架正方向的角度.
位于风速场中的3个叶片上的风速可描述为与风力机方位角以及中心风速有关的3维向量,即v( ,v0)=[v1( ,v0)v2( ,v0)v3( ,v0)]T,vi是第i枚叶片上的等效风速. v( ,v0)描述了3个叶片组成的叶片系风速场.
假设每个叶片上的平均风速点位于叶片中心,即取式(5)中m=2,以此风速作为每个叶片所受风速的平均值. 受风切变的影响,风速标量变为风速场矢量,转矩系数因此不再简单满足式(2)与式(3)的关系,需要相应地作一些修正. 由于风力机总的气动转矩是风速在3个叶片综合作用效果的宏观反应,根据力的作用的等效性,一定可以找到某组等效作用风力(平均作用力),其作用效果与风速场中风力作用效果相同. 因此,可以假设,风力机总的气动转矩为某个叶片的桨距角和相应叶片上的风速分别单独作用到3个叶片上产生的气动转矩的平均值,即:

2.3 风切变场中具有参数不确定的风力机模型
风力机转速ωr、 电磁转矩Te以及电磁功率Pe之间具有以下关系:

设风力机运行在额定功率平衡状态时,额定转速、 额定电磁转矩及额定电磁功率分别为ωr,n、 Te,N、 Pe,N,且具有如下关系:

将式(7)与式(8)相减并对时间t求导,得到如下的功率增量模型:
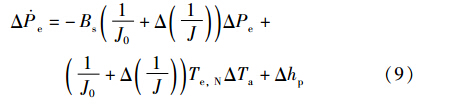
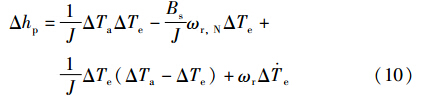
式中,J0为风力机等效惯量J的标称值. 上式说明,电磁功率的变化由空气动力转矩变化、 转速变化和电磁转矩的变化所引起,而在恒电磁转矩的情况下,ΔTe=0,功率模型简化为转速模型,即:
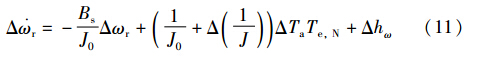

在风切变场中,风速和桨距角不再为标量,而为分布在叶片系中的三维向量,转矩系数中的叶尖速比及桨距角需要重新定义.
若假设空气在风力机整个扫掠面上的分布是均匀的,且经过3个叶片的空气质量为ma,容易得到风力机扫掠面的平均风速为

由此将叶片系中叶尖速比、 叶片的平均桨距角、 功率系数重新定义如下:



为了叙述方便,引入β=[β1 β2 β3]∈B描述某个工作点上桨距角的分布,其中B为桨距角集合. 这里β并非严格意义上的矢量,空间中任意时刻的桨距角向量[1,2,3]∈B,分量i并不表示 在3个叶片轴向上的坐标,仅仅表示某个时刻3个桨距角状态分布情况.
设W和V分别为转速和风速场集合,取工作点op. =(ω rv(,v 0)β ),其中ω r∈W,v( ,v 0)∈V,β ∈B,将ΔTa在工作点op.=(ω rv( ,v 0),β )进行泰勒展开可得
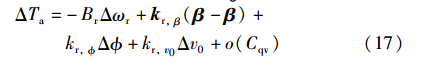
式中:
Br=- Ta ωrop.=Ta(ωr,v( ,v0),β)ωr Cqv(,)/ Cqv(,)/op. kr,β= Ta βTop.= Ta Cqv/ Cqv/ βTop. kr, = Ta op.= Ta vT v op.
=Ta1Cqv Cqv vT+1v2r fr vT v op. kr,v0= Tav0op.= Ta vT v v0op. =Ta1Cqv Cqv vT+ 1v2r fr vT v v0op. fr=v2r=13∑3i=1v2i 从式(7)和式(8)可解出Δωr:
Δho,ω=T-1e,N-ΔTeTe,N+oΔTeTe,N2ΔPe- ωr,NΔTeTe,N1+ΔTeTe,N-1
另外,由于风力发电机中的叶轮转动惯量较大,变桨执行机构可简化为1阶系统,即:

式中βr与β分别为桨距角的给定值和实际值,τ为执行机构的时间常数. 由式(19)可得
β-e=(τs+1)-1βr-e=(τs+1)-1Δβr
式中e=[111],Δβr是桨距角给定增量.
实验证明,方位角 对Br、 kr,v0影响不大,故在这两个数中令 =0,并将ΔTa、 Δωr和Δβr代入式(9),并注意到Δ ·=Δωr,得到

其中
Δp=Bs+BrJ+1+ΔTeTe,N-1-1+BsΔ1J+
ΔBrJΔP·e1τBs+BrJ1+ΔTeTe,N-1-1+
BsΔ1J+ΔBrJ+τΔkr,/sub>JΔPe+
Te,NτΔkr,JΔ -Te,NτΔ(τΔ0+Δv0)+
(Bs+Br)ωr,NτJ(τΔT·e+ΔTe)1+ΔTeTe,N-1+
Te,NΔkr,βJΔβr+1τ(τΔh~·p+Δp)+Te,Nkr,JΔho,ω
当电磁功率不发生变化时,式(20)简化为恒速调节问题,即:
式(20)与式(21)说明,风速及其加速度都会对电磁功率产生影响,而风切变在风力机扫掠面上的分布则会随着风力机方位角的不同对电磁功率产生影响,要想保持恒功率输出,Δβr的控制作用一方面要通过统一变桨抑制风速以及加速度的变化造成的功率波动,另一方面则需要进行周期的独立桨距角调节来抑制风切变作用产生周期性功率波动. 但注意到以上各式中的 可通过直接测量或间接估计的方法得到,因此很容易计算出风切变产生的功率波动.
根据叶素理论,距离风力机中心r处的叶片微元dr所受到的空气动力dF可分解为沿风轮旋转切线方向的力dFu和沿风速方向的气动力dFa,前者产生风力旋转的空气动力转矩,后者是引起叶片拍打振动的主要原因. dFa的具体形式为[16]
式中dS是叶片微元的面积,I=β+i为倾斜角,i是攻角,Cl和Cd分别是桨叶的升力系数和阻力系数,这两个参数一般由风力机生产厂商提供.
由于桨叶的拍打振动在固有频率附近是高频振动,主要影响叶尖的振荡,使得叶尖部分在拍打方向的振荡具有很大的幅度,但对叶片根部的影响并不明显. 因此,可选取叶尖部分来分析桨叶所受气动力. 文[17]给出了叶尖区域的选法,约为叶片总面积的叶尖区域能很好地描述叶尖载荷的空气动力特性,在这块区域内,叶尖所受的风速方向的气动力约为
3 控制策略
额定风速以上恒转速控制的目标是: 当外部环境(如风速、 电磁转矩)或风力机自身参数变化时,风力机依然能在额定转速附近平稳运行,并且控制作用能有效抑制风切变对叶片拍打方向的机械振动. 本文针对风切变情况下的风力机非线性模型,提出一种额定风速以上基于方位角的恒功率独立桨距角控制方法,其控制系统由统一变桨控制器与独立变桨控制器组成,控制框图如图 1所示.
3.1 周期变桨策略
由于风切变的影响,转矩脉动不可避免. 为了消除转矩脉动的影响,最直接和有效的方法就是通过分别改变每个叶片的桨距角,定量补偿每个叶片产生的转矩脉动. 由于风力机中心风速不变时,风切变产生的转矩脉动是周期的,因此每个叶片桨距角的改变也应该是周期的. 这就是本文独立变桨的基本原理.
在叶片运动的一个周期内,气动转矩脉动是关于方位角对称的,气动转矩脉动为0时对应的方位角位于气动转矩脉动为最大值与最小值对应的方位角的中心点上. 选取风力机运行一周内关于方位角的12个工作点进行线性化,即为 =π/6×i,i=0,…,11.
式(17)中kr, Δ 项表征风切变作用在3个叶片上引起的空气动力转矩波动的总和. 而如果能将kr, Δ 分解为风切变作用在每个叶片上引起的空气动力转矩波动,则调节响应叶片的桨距角就可抑制空气转矩波动来达到平滑功率的目的. 这就是本文独立桨距角调节的基本目的和思路.
kr, 的标称值kr, ,0可分解为kr, ,0=∑3i=1kr, ,0,i,而kr,β的标称值也可分解为[kr,β,0,1kr,β,0,2kr,β,0,3],其中,
kr, ,0,i=Ta1Cqv,0· Cqv,0 · vi+1vr2· fr vi vi op.
Δβr,β,0,i=Ta· Cqv,0/ Cqv,0/· βiop.
将以上关系代入式(20)中,设每个叶片上的补偿控制量为Δβr,ind,i,令:
则由风切变引起的转矩脉动可被完全消除,即为周期独立桨距角调节增量信号. Δ 可以这样确定: 先确定方位角属于哪个工作区域,再确定在该区域中的偏移量,即:
式中rnd(·)为舍入函数.
ADRC是一种基于状态观测与扰动补偿的非线性控制器,由跟踪微分器(TD)、 扩张状态观测器(ESO)、 状态误差反馈(SEF)以及扰动估计补偿(DEC)4个部分组合而成. 其中跟踪微分器(TD)为参考信号安排过渡过程并基于广义微分理论提取其微分; 扩张状态观测器(ESO)估计系统状态、 外部扰动和模型不确定性; 状态误差反馈(SEF)和扰动估计补偿(DEC)用于根据反馈误差配置非线性控制结构并产生控制信号.
针对式(20)2阶系统的ADRC控制器为[16]:
(1) 以设定值w*r为输入,安排过渡过程(27),额定风速以上时,式(20)是一个恒值调节问题,因此w*r为常值,从而Δw*r≡0,跟踪微分器简化为式(28).
(2) 以系统输出和输入来跟踪
(3) 状态误差反馈律
式中θ=θ(α1,α2,β)为控制器的设计参数,k是e1、 e2与θ的非线性函数,这里取为
(4) 扰动补偿
以上各式中
sat(a,δ)=sgn a,a>δ,a/δ,a<δ
fal(e,α,δ)=eαsgn e,e>δ
e/δ1-α,e≤δ b0根据式(20)取为b0=J-10kr,β,0(ω r,v( ,v 0),β ).
为验证本文所提出控制方法的有效性,选取2 MW永磁同步风力发电机进行仿真研究,机组主要参数的标称值如表 1所示; 升力系数Cl、 阻力系数Cd、 翼型和叶片面积使用GH Bladed软件仿真得到. 统一变桨控制的工作点选为: (ω r,v 0,β )=(1.738 rad/s,13 m/s,[1.572° 1.572° 1.572°]T); 自抗扰控制器参数整定为α1=0.9,α2=1.3,δ=0.1,β01=100,β02=10 000,β03=1 000,β1=2 400,β2=400.
仿真实验对比了文[11]中的权系数分配方案,传统的PID控制器,以及统一变桨方案的性能. PID控制器的参数整定为: kP=1 000,kI=2 000,kD=100.
以下各图中,′Pro.′,′W.A′,′PID′和′Col.′分别表示本文方法,权系数分配方法,PID方法和传统统一变桨方法.
4.1.1 统一变桨信号对独立变桨作用的影响
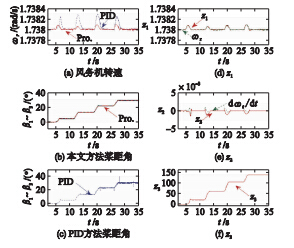
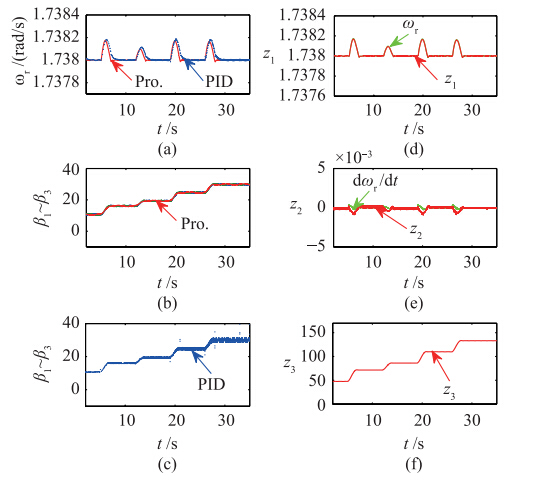
假设风力机中心风速v0变化如图 2(a)所示,图 3是本文方法和权系数方法的仿真曲线. 从图中可以看出,两种方法都能通过调节桨距角来维持转速恒定,但随着风速增加,统一变桨信号的振动幅度逐渐增大,权系数方法得到的独立变桨信号的幅度也成倍地增大,当风速增大到20 m/s,桨距角调节频率已达到12 °/s. 而变桨执行机构的变桨速度是有限制的,因此随着变桨幅度的增大,其控制性能将会降低. 本文的控制信号是统一变桨信号之上叠加的幅值恒定的信号,其幅度仅与风力机的方位角有关,当统一变桨信号的振荡幅度增大时不会影响到独立变桨信号偏离统一变桨信号的幅度. 因此本文方法的桨距角控制量在额定风速以上较大范围内都比较平稳.
图 4、 5是在如图 2(b)所示的一段风速的作用下,本文独立桨距角调节方法、 权系数方法及集中桨距角调节方法的桨距角变化叶片拍打方向上气动载荷的对比仿真结果. 从图 4可以看到,权系数分配方法的桨距角调节幅度和频率受其统一变桨信号幅度和频率的影响,因而当统一变桨信号的频率和幅度较大时,权系数分配方法的独立桨距角信号的幅度和频率也很大. 长时间按照此方式工作,对叶片执行机构是一个巨大的考验,容易降低叶片的使用寿命. 而本文的独立桨距角调节方法中,独立变桨信号是“加”到统一变桨信号上,因而其幅值和频率不受统一变桨信号的影响. 可以看到,本文方法的独立桨距角调节信号更加平顺.
图 5说明,尽管权系数分配方法和本文方法都能有效减小叶片拍打方向的气动载荷,但本文方法的减载效果更明显. 这是因为,权系数分配方法是靠大范围调节桨距角来降低气动载荷的(图 4),由前面的分析可知,当统一变桨信号的震荡幅度较大时,其独立变桨的幅度也将变得很大,这将会造成独立调节作用“超调”. 另一方面,权系数分配方法将使得变桨执行机构在大部分时间里处于高转矩的工作状态,换言之,这种方法是通过增加叶片的扭转载荷来减小拍打载荷的,长期工作将影响叶片的使用寿命. 本文方法在桨距角调节的频率和高转矩之间取得了不错的平衡,相对于传统的统一变桨方法降低了桨距角调节的频率,相对于权系数分配方法又缩短了处于高转矩工作状态的时间. 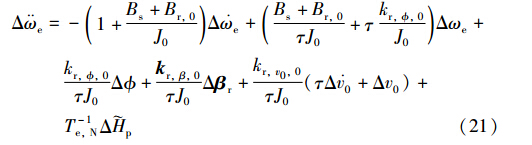
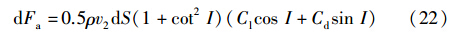

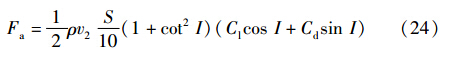
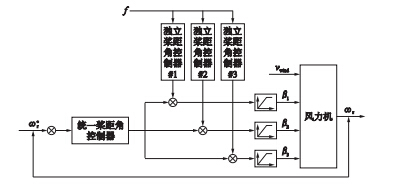
图 1 控制框图Fig. 1 Control scheme 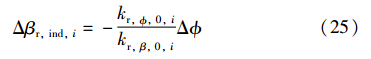
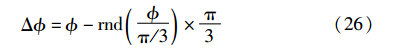

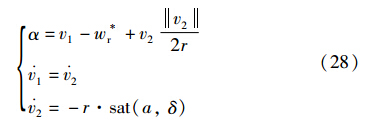
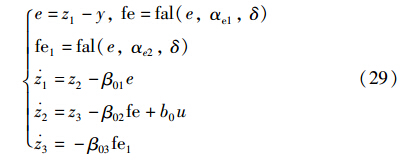
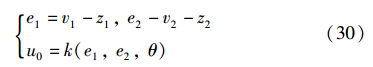
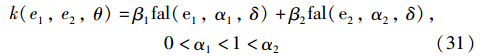

风力机参数 值
风力机半径 36 m
额定功率 2 MW
发电机极对数 28
摩擦系数 15.1
风速范围 3 m/s~25 m/s
额定风速 12 m/s
变桨时间常数 0.5 s
桨距角最大调节速度 15 °/s
空气密度 1.225 kg/m3 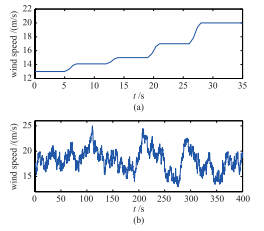
图 2 输入风速Fig. 2 Input wind speed 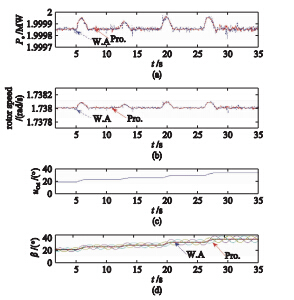
图 3 统一变桨信号对独立变桨的影响Fig. 3 Impacts on individual pitching of collective pitching signal
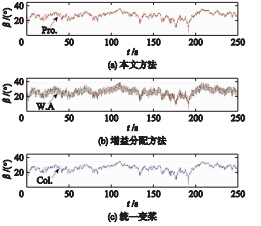 |
| 图 4 桨叶桨距角变化曲线Fig. 4 The curves of blade angle |
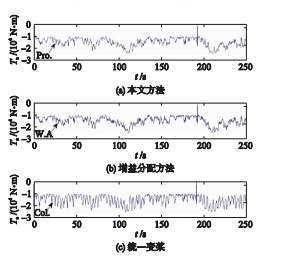 |
| 图 5 叶片拍打方向的气动载荷Fig. 5 The flapwise aerodynamic loads of blade |
4.2 鲁棒性能
4.2.1 对风速变化和电磁转矩扰动的鲁棒性
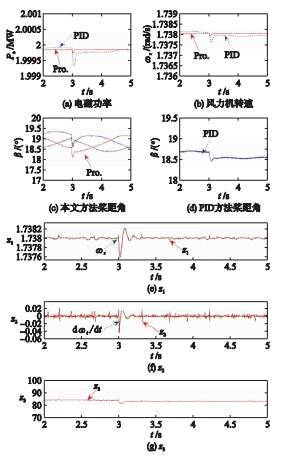
设电磁转矩与风力机参数保持恒定,风速如图 2(a)所示. 图 6是本文方法与PID控制的仿真结果. 可以看到,风速不大时,两种方法都能通过调节桨叶桨距角来维持转速恒定,随着风速不断增大,PID控制下的转速出现了较为剧烈的波动. 而本文方法控制下,转速始终比较平稳. 这是因为风力发电系统的强非线性特性,当风速偏离预设工作点风速时,系统与预设工作点之间的模型偏差在逐步增大,虽然PID控制器的增益裕度或相角裕度能保证一定范围内的模型偏差下系统的鲁棒性,但是当模型偏差增大到一定程度而超过PID的裕度范围时,鲁棒性被破坏,控制器的性能急速下降. 而自抗扰控制由于能较准确地估计模型偏差,因此即使风速大大偏离预设工作点,控制性能依然能得到保证.
 |
| 图 6 对风速变化的鲁棒性Fig. 6 Robustness to the variation of wind speed |
当电磁转矩在3 s时出现10 000 N·m的转矩扰动,从图 7(e)~7(g)可以看到,ESO能准确估计出电磁转矩扰动. 相比于PID方法,图 7(a)~7(d)表明在本文方法控制下,电磁功率和风力机转速更加平稳. 说明本文方法比PID方法具有更强的抗外部干扰能力.
4.2.2 对参数变化的鲁棒性假设风力机参数变化为KCqv=2×K0Cqv,0,J=0.8×J0. 图 8是电磁转矩保持恒定,本文方法与PID方法的仿真结果.
 |
| 图 7 对电磁转矩变化的鲁棒性Fig. 7 Robustness to the electromagnetic ripples |
 |
| 图 8 对参数变化的鲁棒性Fig. 8 Robustness to the change of parameters |
可以看到,当参数变化时,PID控制器对桨距角β的调节过于频繁,从而抑制参数变化和电磁转矩变化的影响. 而本文方法中,集中桨距角控制器通过ESO对模型不确定部分进行估计,相对于标称系统,控制量仅增加了由于参数变化而导致的模型偏差. 桨距角除了周期独立调节以外,针对参数变化的调节并不频繁,说明本文方法对参数变化有更好的鲁棒性.
5 结语基于风切变模型,提出了一种额定风速以上独立变桨鲁棒控制方法. 理论分析和仿真结果表明,基于该方法设计的控制器具有以下特点:
(1) 在额定以上较大风速范围内实现恒转速控制,并且对参数不确定性具有较强的鲁棒性;
(2) 控制器对风切变造成的转速波动及叶片拍打方向的机械载荷具有较好的抑制效果;
(3) 独立桨距角调节效果不受统一变桨信号频率和振幅的影响.
与其它的非线性方法,如神经网络方法[18]、 逆系统方法[19, 20]等相比,本文方法不需要测量风速,控制器更加简单直观、 物理含义明确、 方便工程转化.
| [1] | 何玉林, 吕向飞, 黄帅, 等. 变速变桨风力发电机组的优化控制[J]. 可再生能源, 2012, 30(1): 33-37. He Y L, Lü X F, Huang S, et al. Optimal control of variable speed variable pitch wind turbine[J]. Renewable Energy Resources, 2012, 30(1): 33-37. |
| [2] | 邬开俊, 王铁君. 变速恒频无刷双馈风力发电机及其控制[J]. 信息与控制, 2010, 39(3): 348-353. Wu K J, Wang T J. Control of variable speed constant frequency brushless doubly fed wind power generator[J]. Information and Control, 2010, 39(3): 348-353. |
| [3] | 韦徵, 陈冉, 陈家伟, 等. 基于功率变化和模糊控制的风力发电机组变速变桨距控制[J]. 中国电机工程学报, 2011, 31(17): 121-126. Wei Z, Chen R, Chen J W, et al. Wind turbine-generator unit variable-speed pitch control based on judgment of power changes and fuzzy control[J]. Proceedings of the CSEE, 2011, 31(17): 121-126. . |
| [4] | Jelavic M, Petrovic V, Peric N. Estimation based individual pitch control of wind turbine[J]. Automatika, 2010, 51(2): 181-192. |
| [5] | Namik H, Stol K. Individual blade pitch control of floating offshore wind turbines[J]. Wind Energy, 2010, 13(1): 74-85. |
| [6] | Cheng B, Deng X, Hedrick T L. The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta)[J]. The Journal of experimental biology, 2011, 214(24): 4092-4106. |
| [7] | 刘其辉, 贺益康, 赵仁德. 变速恒频风力发电系统最大风能追踪控制[J]. 电力系统自动化, 2003, 27(20): 62-67. Liu Q H, He Y K, Zhao R D. The maximal wind energy tracking control of a variable speed constant frequency wind power generation system[J]. Automation of Electric Power Systems, 2003, 27(20): 62-67 |
| [8] | Senjyu T, Sakamoto R, Urasaki N, et al. Output power leveling of wind turbine generator for all operating regions by pitch angle control[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 467-475. |
| [9] | Bossanyi E A. Individual blade pitch control for load reduction[J]. Wind Energy, 2003, 6(2): 119-128. |
| [10] | Selvam K, Kanev S, van Wingerden J W, et al. Feedback-feedforward individual pitch control for wind turbine load reduction[J]. International Journal of Robust and Nonlinear Control, 2009, 19(1): 72-91. |
| [11] | 林勇刚, 李伟, 陈晓波, 等. 大型风力发电机组独立桨叶控制系统[J]. 太阳能学报, 2005, 26(6): 780-786. Lin Y G, Li W, Chen X B, et al. The research on large scale wind turbine individual blade pitch control system[J]. Acta Energiae Solaris Sinica, 2005, 26(6): 780-786. |
| [12] | 姚兴佳, 刘玥, 郭庆鼎. 基于前馈补偿方位角权系数的分程独立变桨距控制研究[J]. 太阳能学报, 2012, 33(4): 532-539. Yao X J, Liu Y, Guo Q D. A control method for split range individual pitch based on feed-forward azimuth angle weight number assignment[J]. Acta Energiae Solaris Sinica, 2012, 33(4): 532-539. . |
| [13] | Delarue P, Bouscayrol A, Tounzi A, et al. Modelling, control and simulation of an overall wind energy conversion system[J]. Renewable Energy, 2003, 28(8): 1169-1185. |
| [14] | Gasch R, Twele J. Wind power plants: Fundamentals, design, construction and operation[M]. 2nd ed. Berlin, Germany: Springer, 2011. |
| [15] | 马惠群, 曲宁, 李超, 等. 风电场风切变指数研究[J]. 电网与清洁能源, 2012, 28(6): 88-90. Ma H Q, Qu N, Li C, et al. Study on wind shear exponents of wind farms[J]. Power System and Clean Energy, 2012, 28(6): 88-90. |
| [16] | 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 第1版. 北京: 国防工业出版社, 2008. Han J Q. Active disturbance rejection control technique-The technique for estimating and compensating the uncertainties[M]. 1st ed. Beijing: National Defense Industry Press, 2008. . |
| [17] | Bolognani S, Tubiana L, Zigliotto M. Extended Kalman filter tuning in sensorless PMSM drives[J]. IEEE Transactions on Industry Applications, 2003, 39(6): 1741-1747. |
| [18] | Yilmaz A, Ozer Z. Pitch angle control in wind turbines above the rated wind speed by multi-layer perception and radial basis function neural networks[J]. Expert Systems with Applications, 2009, 36(6): 9767-9775. |
| [19] | 刘向向, 李新宇, 王奔, 等. 变结构控制策略在直驱永磁同步风力发电机中的应用[J]. 电网技术, 2013, 37(2): 520-525. Liu X X, Li X Y, Wang B, et al. Application of variable structure control strategy in direct-drive permanent magnet synchronous wind turbine generator[J]. Power System Technology, 2013, 37(2): 520-525.. |
| [20] | 耿华, 周伟松, 杨耕. 变桨距风电系统功率控制的逆系统鲁棒方法[J]. 清华大学学报: 自然科学版, 2010, 50(5): 718-723. Geng H, Zhou W S, Yang G. Inverse system based robust approach for power control of variable-pitch wind generation system[J]. Journal of Tsinghua University: Science & Technonlgy, 2010, 50(5): 718-723. . |



