2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
预测控制是20世纪70年代末期发展起来的一种基于模型的控制算法,经过多年的研究与应用,已成为一种重要的现代控制方法[1 -4]. 模型精度是影响预测控制性能的一个重要因素,而实际工程系统由于条件受限与噪声干扰等原因,难以建立精确的系统模型. 针对这种模型不确定性问题,文[5]最先结合预测控制与子空间辨识算法N4SID(numerical algorithms for subspace state space system identification),提出了子空间预测控制算法SPC(subspace predictive control). SPC算法仅通过输入输出数据就能实现不依赖模型的预测控制,因此能够避免建模精度对控制性能的影响. 目前,这种完全数据驱动的算法已得到越来越多的研究与应用[6 -9].
实际工程系统的时变特性也会造成模型不确定性问题,往往需要进行自适应控制才能达到期望的控制效果. 不少学者在SPC算法的基础上,结合递推子空间辨识方法,研究自适应预测控制方法[10 -13]. 但因为N4SID算法是一种开环子空间辨识算法,当系统闭环且存在噪声时,N4SID算法会出现估计偏差[14],所以这类基于SPC算法的自适应预测控制方法并不适用于闭环且存在噪声的系统. 另一方面,子空间辨识方法涉及较多的矩阵运算,为提高在线计算效率,目前主要采用的方法是用Givens旋转方法进行快速LQ分解更新[10 -12],另外还有用Cholesky分解代替LQ分解[15]、 快速滑动窗口[16 -17]等方法. 虽然采用这些矩阵分解修正方法能够提高计算效率,但也难以避免要考虑其过于复杂、 数值稳定性与迭代收敛性等问题.
文[18]提出了闭环子空间预测控制算法CLSPC(closed-loop subspace predictive control),该算法避免了SPC算法的问题,适用于闭环且存在噪声干扰的系统. 本文在CLSPC算法的基础上,提出了一种自适应预测控制方法. 通过结合PID控制,采用新的目标函数,对CLSPC算法进行改进,并采用固定输入输出数据集大小的递推方法将改进后的算法在线实施. 为提高在线计算效率,根据输入输出数据组成的Hankel矩阵与相应LQ分解的L矩阵的特点,采用一种简单直观的方法进行系统马尔可夫参数矩阵的更新. 最后,通过仿真验证方法的有效性.
2 改进的闭环子空间预测控制算法考虑如下线性离散系统:
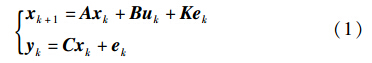
式中,xk∈Rn,uk∈Rm,yk∈Rl,ek为零均值高斯白噪声序列.
若已知系统p+N-1对数据{uk,yk},构造Hankel矩阵Yk=[yk yk+1 … yk+N-1]与Zp=[UTk-p YTk-p …UTk-1 YTk-1]T. 记=A-KC,Ξ0=[Cp-1B Cp-1K… CB CK]为系统马尔可夫参数矩阵,其最优估计值Ξ^0可由Yk与Zp求解:
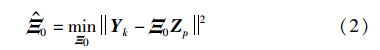
记p [uTk-pyTk-p…uTk-1yTk-1]T,uf [uTkuTk+1…uTk+f-2]T,分别表示在控制作用k时刻的过去输入输出序列与将来控制输入序列. k时刻的将来输出序列的最优估计值f [Tk+1Tk+2…Tk+f-1]T可由以下输出预测器得到:
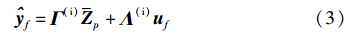
矩阵Γ(i)与Λ(i)由Ξ^0构造,具体可见文[18].
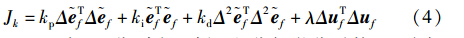
式中,kp、 ki与kd分别为比例、 积分与微分系数,λ为加权系数,Δ为差分算子,误差序列f=rf-f,rf [rTk+1rTk+2…rTk+f-1]T为参考输入柔化序列,由下式构造得到:

其中,0≤α<1为柔化因子,dk为参考输入.
由式(3)可得:

式中,Uk-1
uk-1
uk-1k-1,
Sm=Im
Im…Im.
记(i) Λ(i)·Sm,由式(5)知Δk=k=0,则有:
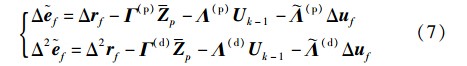
式中,Δrf rTk+1ΔrTk+2…ΔrTk+f-1T,Δ2rf与Δrf类似定义; M(τ,: )表示矩阵M的第τ行向量,
Γ(p)=
Γ(i)(1,: )
Γ(i)(2,: )-Γ(i)(1,: )
Γ(i)(f-1,: )-Γ(i)(f-2,: )
Γ(d)=
Γ(p)(1,: )
Γ(p)(2,: )-Γ(p)(1,: )
Γ(p)(f-1,: )-Γ(p)(f-2,: )
矩阵Λ(p)和(p)与Γ(p)类似,矩阵Λ(d)和(d)与Γ(d)类似.
将式(6)、 (7)代入式(4),令 Jk Δuf=0,可得:

式中,Rp=kpΩ((p))T,Ri=kiΩ((i))T,Rd=kdΩ((d))T, Ω=(λI+kp((p))T(p)+ki((i))T(i)+kd((d))T(d))-1.
将式(8)与常规数字PID控制律

比较可知,式(8)与式(9)具有类似的结构.
3 自适应预测控制方法如图 1所示,在线作用时,通过实时更新系统马尔可夫参数矩阵Ξ^0,进而实现控制律的更新. Ξ^0由数据集{uk,yk}构造的Hankel矩阵计算得到,本文采用保持数据集大小不变的方法,即往数据集中增加新收集的数据的同时,剔除数据集中最早的旧数据,这样可避免因数据累积而使在线计算量不断增大.
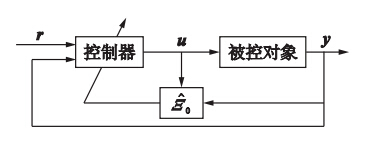 |
| 图 1 自适应预测控制框图Fig. 1 Block of adaptive predictive control |
式(2)最小二乘问题由LQ分解进行求解:

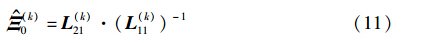
LQ分解计算量较大,为提高计算效率,通常采用Givens旋转方法进行快速LQ分解更新:
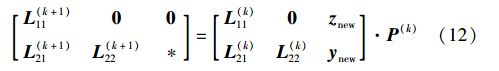
式中,P(k)为一系列Givens旋转矩阵的乘积,znew和ynew为接收新数据时Zp与Yk分别增加的新向量. 当剔除旧向量zold和yold时,再由相同原理进行一次更新. Givens旋转方法虽然能提高计算效率,但相对较为复杂. 本文采用一种简单直观的方法即可实现Ξ^0的更新.
接收新数据且剔除旧数据后,有如下关系:

将上式视为[H1h2]=[h3H4],记L(k)1 L(k)11·(L(k)11)T与L(k)2 L(k)21(L(k)11)T,L1与L2的更新关系可由式H1HT1+h2hT2=h3hT3+H4HT4化简得到:

同时,由式(11)可得Ξ^0的更新关系:

LQ分解方法、 Givens旋转方法和本文方法分别由式(10)与式(11)、 式(12)与式(11)和式(14)与式(15)更新Ξ^0矩阵. 式(11)和式(15)的计算复杂度一样,记 p(m+l)(通常取值<
具有类似PID结构的闭环子空间自适应预测控制器(PID-ACLSPC)实现步骤如下:
Step 0: 设定相关参数,离线准备初始数据集,计算矩阵L1与L2的初始值;
Step 1: 收集当前k时刻的系统输入输出数据,构建向量znew、 ynew、 zold与yold;
Step 2: 由式(14)更新矩阵L1与L2;
Step 3: 由式(15)更新矩阵Ξ^0;
Step 4: 由式(8)计算控制序列,取其第一个量为系统控制输入;
Step 5: k=k+1,转Step 1.
考虑如下的2阶和5阶慢时变线性系统:
x(1)k+1=
0.6+0.03sin k0.479 13
-0.323 860.882 92x1k+
-0.029 472
0.011 775u1k+
0.003 574 7
0.007 152 1e1k y1k=[10.878112.15]x1k+e1k x2k+1=
1+0.1sin k-0.023 492-0.007 655-0.001 570-0.000 760
0.02+0.01sin k0.984 52-0.138 86-0.012 6910.035 256
0.015 5670.159 560.948 18-0.029 7080.035 529
0.000 969 1-0.010 768-0.004 9270.779 710.626 37
0.005 973-0.012 717-0.163 28-0.567 870.687 49x2k+
0
-0.000 657
0.001 783
0.000 079
0.002 675u2k+
[0.000 113-0.001 784-0.001 539-0.012 0310.001 031]Te2k y1k=[12 500+100sin k-147.01-43.826-8.954 4-7.114 2]x2k+e2k
其中,E((e1k)2)=0.1,Ε((e2k)2)=0.05.
p、 f、 N与PID参数等参数对PID-ACLSPC的控制性能影响较大,选择不当甚至有可能造成闭环不稳定. 但这些参数隐含在矩阵中,难以推导出其与性能之间的显式关系,可参考文[15]与文[20],通过反复实验总结出参数变化影响性能的规律,再根据系统进行调试确定.
图 2与图 3为PID-ACLSPC与GPC(generalized predictive control)和ACLSPC的控制效果对比,表 1为超调量百分比(P.O.)、 上升时间(Tr)与时间乘误差平方积分(ITSE)等性能指标的对比. 可以看出,GPC输出波动较大,ACLSPC与PID-ACLSPC都能较好地克服系统参数变化跟踪参考输入,同时比较易知,PID-ACLSPC能够较好地抑制超调,快速跟踪参考输入,减小跟踪误差.

图 2 y1输出跟踪效果Fig. 2 Output tracking performance of y1 
图 3 y2输出跟踪效果Fig. 3 Output tracking performance of y2
y1 y2
P.O. Tr ITSE P.O. T r ITSE
GPC 20.8% 16 2.76×104 19.3% 17 3.41×104
ACLSPC 11.8% 12 2.18×104 15.4% 15 2.75×104
PID-ACLSPC 4.5% 6 1.14×104 8.6% 8 1.64×104
本文提出了一种完全数据驱动的基于递推闭环子空间辨识的自适应预测控制方法. 对计算复杂度的分析表明,该方法具有较高的计算效率. 仿真结果表明该方法能够对存在噪声干扰的线性时变系统进行良好控制,结合PID控制采用新的目标函数对CLSPC算法进行的改进能够有效提高控制性能.
| [1] | 胡耀华, 贾欣乐. 广义预测控制综述[J]. 信息与控制, 2000, 29(3): 248-256. Hu Y H, Jia X L. Summarization of generalized predictive control[J]. Information and Control, 2000, 29(3): 248-256. |
| [2] | 席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3): 222-236. Xi Y G, Li D W, Lin S. Model predictive control-Status and challenges[J].. Acta Automatica Sinica, 2013, 39(3): 222-236 |
| [3] | 李锐, 方洋旺, 蔡文新, 等. 随机系统预测控制稳定性分析及快速预测算法[J]. 信息与控制, 2013, 42(2): 145-151. Li R, Fang Y W, Cai W X, et al. Stability analysis and a fast algorithm for the predictive control of stochastic systems[J]. Information and Control, 2013, 42(2): 145-151. |
| [4] | 杨世忠, 任庆昌. 基于在线优化的鲁棒模型预测控制[J]. 信息与控制, 2013, 42(6): 742-749. Yang S Z, Ren Q C. Robust model predictive control based on online optimization[J]. Information and Control, 2013, 42(6): 742-749. |
| [5] | Favoreel W, Moor D B. SPC: Subspace predictive control[C]//Proceedings of the 14th IFAC World Congress. Oxford, UK: Pergamon Press, 1998: 235-240. |
| [6] | Kadali R, Huang B, Rossiter A. A data driven subspace approach to predictive controller design[J]. Control Engineering Practice, 2003, 11(3): 261-278. |
| [7] | 王宇红, 王学剑. 基于协方差基准的模型预测控制性能评价与监视[J]. 信息与控制, 2010, 39(6): 694-699. Wang Y H, Wang X J. Performance assessment and monitoring of model predictive control based on covariance benchmark[J]. Information and Control, 2010, 39(6): 694-699. |
| [8] | Mardi N A, Wang L P. Subspace-based model predictive control of time-varying systems[C]//Proceedings of the 48th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2009: 4005-4010. |
| [9] | Wu X, Shen J, Li Y G, et al. Data-driven modeling and predictive control for boiler-turbine unit[J]. IEEE Transactions on Energy Conversion, 2013, 28(3): 470-481. |
| [10] | 孙磊, 金晓明. 基于子空间辨识的模型预测控制策略及其应用[J]. 控制理论与应用, 2009, 26(3): 313-315. Sun L, Jin X M. Model-predictive-control based on subspace identification and its application[J]. Control Theory & Applications, 2009, 26(3): 313-315. |
| [11] | 谢志刚, 陈自力, 何应德. 无人动力伞在线子空间模型预测控制[J]. 信息与控制, 2011, 40(6): 841-845. Xie Z G, Chen Z L, He Y D. Online subspace predictive control of unmanned powered parafoil[J]. Information and Control, 2011, 40(6): 841-845. |
| [12] | Wahab N A, Katebi R, Balderud J, et al. Data-driven adaptive model-based predictive control with application in wastewater systems[J]. IET Control Theory and Applications, 2011, 5(6): 803-812. |
| [13] | 张立, 高宪文. 递推子空间自适应预测控制综合方法[J]. 信息与控制, 2012, 41(4): 439-453. Zhang L, Gao X W. A Synthesis method of adaptive predictive control based on recursive subspace[J]. Information and Control, 2012, 41(4): 439-453. |
| [14] | Overschee V P, Moor D B. Closed loop subspace system identification[C]//Proceedings of the 36th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 1997: 1848-1853. |
| [15] | Woodley B R. Model free subspace based H∞ control[D]. Stanford, USA: Stanford University, 2001. |
| [16] | Liang W X, Kruger U, Wang X, et al. Fast moving window algorithm for QR and cholesky decompositions[C/OL]//Proceedings of the 17th IFAC World .Congress. (2012-07-06)[2014-03-01] |
| [17] | 谢磊, 梁武星, 张泉灵, 等. 基于快速滑窗QR分解的自适应子空间辨识[J]. 化工学报, 2008, 59(6): 1449-1453. Xie L, Liang W X, Zhang Q L, et al. Adaptive subspace identification based on fast moving window QR decomposition[J]. Journal of Chemical Industry and Engineering, 2008, 59(6): 1449-1453. |
| [18] | Dong J F, Verhaegen M, Holweg E. Closed-loop subspace predictive control for fault tolerant MPC Design[C/OL]//Proceedings of the 17th IFAC World Congress. (2010-11-06)[2014-03-01]. |
| [19] | 张俊, 罗大庸. 广义预测控制和PID控制在混凝投药中的应用[J]. 信息与控制, 2012, 41(1): 89-94. Zhang J, Luo D Y. The application of GPC control and PID control to coagulant dosing[J]. Information and Control, 2012, 41(1): 89-94. |
| [20] | 郭伟, 王伟. PID型广义预测控制在过热温控中的应用[J]. 计算机工程, 2009, 35(11): 251-253. Guo W, Wang W. Application of PID-type generalized predictive control in superheated temperature control system[J]. Computer Engineering, 2009, 35(11): 251-253. |



