2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引 言
磷酸亚铁锂电池以其寿命长、 容量大、 放电平稳、 安全性高等优点备受关注. 但因锂电池特性的高度非线性和时变性等原因,精确建模难度大,影响了锂电池的应用推广[1, 2, 3, 4]. 目前,国内外已提出较多电池模型,其中等效电路模型以其参数少、 参数辨识容易、 直观方便等优势被广泛采用. 典型的等效电路模型有内阻(Rint)模型、 电阻电容(RC)模型、 Thevenin模型、 新一代汽车伙伴关系(PNGV)模型及通用非线性(GNL)模型等[5]. Rint模型是最简单的等效电路模型,仅由开路电压和电池内阻两部分组成. RC和Thevenin模型为线性模型,只能表示电池在某个荷电状态(state of charge,SOC)下的暂态响应,动态性能差. PNGV和GNL模型是非线性模型,暂态和动态性能均优于前几种模型,但PNGV模型在不同温度和SOC等情形下模拟精度迥异,在低SOC段误差较大. GNL模型虽在各种SOC状态下均有较高的模拟精度,但由于该模型相当复杂,参数较多、 辨识难度大、 复杂度高,实际应用困难. 目前尚无一种参数少、 简单易行、 适用范围广且精度高的锂电池等效电路模型[6, 7].
本文提出一种基于多输入多输出(MIMO)模糊控制的参数自适应等效电路模型(fuzzy adaptive parameters equivalent-circuit model of Li-ion battery,FAP)的建立方法,使用该模型不仅能在锂电池SOC全区间精确建模,还能自适应地调整模型参数,降低温度等外部因素带来的影响,为解决锂电池均衡管理和全过程精确估计锂电池SOC、 健康状态(SOH)等问题奠定了基础.
2 自适应模型原型选择 2.1 模型分析除第1节中提到的几种典型模型外,近年又有许多学者提出了一些新的等效电路模型,如电阻电量(RQ)模型、 动态参数(DP)模型等,这些模型都是通过增加不同电路元件,以求达到对电池稳态和瞬态的最佳模拟[8, 9, 10, 11, 12, 13, 14, 15]. 本文选择PNGV模型作为自适应模型原型,主要原因有以下几点: (1) PNGV模型在高SOC区间内能较好地描述电池的瞬态响应; (2) 模型形式简单,参数易于辨识; (3) 模型中各参数意义明确; (4) 通过修正该模型中的参数能达到其它复杂模型在某些环境条件和特定工况下的描述效果; (5) 与某些复杂模型的简化模型相似. PNGV等效电路模型[5]如图 1所示.
 |
| 图 1 PNGV等效电路模型Fig. 1 PNGV equivalent-circuit model |
模型中Uoc为电池开路电压,随SOC不同而变化; R0为欧姆内阻; R1为电池极化阻抗; C1为极化阻抗周围电容;Cb表征开路电压与负载电流的时间积分变化关系.
由锂电池的电极平均电化学模型(EAM)可知,影响电池瞬态和稳态端电压的因素主要有温度、 欧姆极化、 电化学极化和浓差极化等,而PNGV模型仅描述了部分影响因子,只能反映形成瞬态和稳态响应的部分机理[12]. 通过分析复杂的通用型非线性GNL模型[5](如图 2所示)可发现: 该模型采用电池不同状态使用不同支路结构的方式来提高模型的适应能力,GNL模型在不同状态下的等效电路能由PNGV模型通过修正参数来近似逼近. 由此可知,通过自适应地修正PNGV模型参数,采用等效电路的时间常数和阻抗与电池实际参数相匹配的方式来精确描述锂电池的SOC全区间模型是可行的.
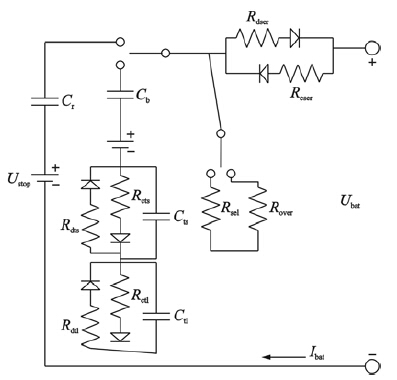 |
| 图 2 GNL等效电路模型Fig. 2 GNL equivalent-circuit model |
由基尔霍夫电压定律和电流定律,可得PNGV模型方程:
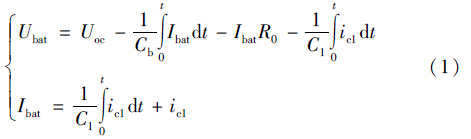
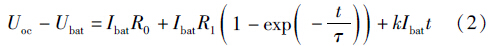
根据文[6]提出的辨识方法,通过激励—响应来进行分析,即根据已知输入电流—输出的电压情况来计算电池模型中各参数.
电池激励信号采用20 A,持续时间15 s的脉冲电流,放电结束后静置60 s,电池端电压响应示意曲线如图 3所示,再采用最小二乘曲线拟合技术,可辨识出模型参数.
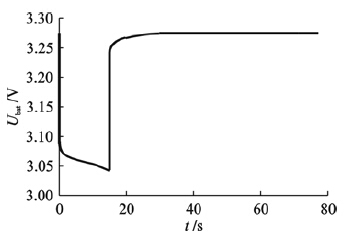 |
| 图 3 PNGV模型响应示意曲线Fig. 3 Schematic curve of PNGV model′s response |
由式(2)可知,模型中需调整的参数有4个:R0、 R1、 k和τ. 为设计调节器,需先明确锂电池模型状态的变化及4个参数的变化趋势.
实验方法: 在25°实验环境下,将锂电池充满,以0.5 C的放电电流将电池的SOC调整至90%,80%,…,20%,10%,每次调整结束后充分静置,以得到下次放电起始时刻的准确Uoc,记录相关数据; 之后以1 C、 1.5 C的放电电流重复以上实验. 采用2.2节中的辨识方法分别辨识出电池在不同起始SOC下以不同电流放电的模型参数R0、 R1、 k和τ[12, 15].
(1) R0的辨识. 分析图 4可得到以下结论: ① 随SOC的减小,R0增大. 在小放电倍率情况下这一趋势不太明显,变化很小; 在大放电倍率下,变化较大. ② 在高SOC区间,R0变化不大; 在低SOC区间,R0变化大. ③ 在相同SOC情形下,放电倍率越大,欧姆内阻越小.
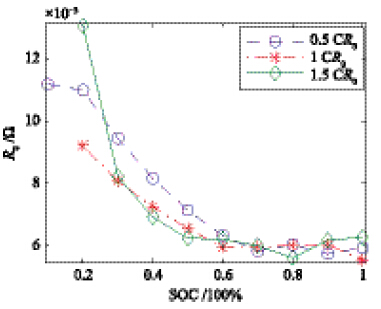 |
| 图 4 R0辨识结果Fig. 4 R0 identification results |
(2) R1的辨识. 由图 5可知,当SOC大于0.4时,R1基本稳定,可看作是常量; 当SOC小于0.4时,R1略有增加,但总体集中在7 mΩ~16 mΩ之间.
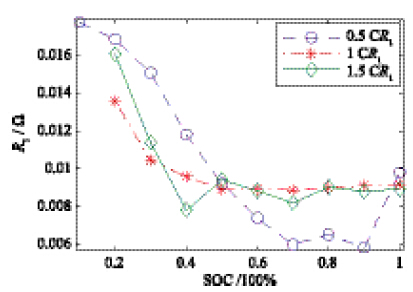 |
| 图 5 R1辨识结果Fig. 5 R1 identification results |
(3) k的辨识. 根据图 6可知,参数k的变化规律: ① 当SOC大于0.4时,k基本不变. ② 当SOC从0.4不断向下减小时,k以指数规律增加. ③ 放电倍率对k影响不大.
 |
| 图 6 k辨识结果Fig. 6 k identification results |
(4) τ的辨识. 由图 7可得以下结论: ① 电池放电倍率越大,时间常数越小. ② 电池SOC越小,时间常数越大. 另外,时间常数τ仅反映了部分瞬态响应,许多优化的复杂模型处理办法是通过添加RC并联元件组来改良模型精度. 本文的处理办法是采用动态修正τ的方式来提高模型精度.
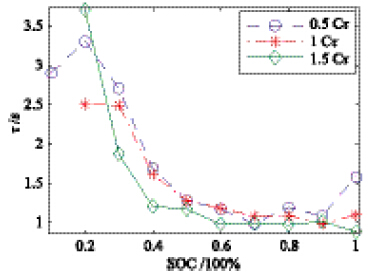 |
| 图 7 τ辨识结果Fig. 7 τ identification results |
(5) 外界因素的影响. 锂电池是温度敏感型的,在不同温度下性能差异较大. 文[12]指出,不同温度会导致锂电池的充放电内阻不同,最大差异可达0.02 Ω. 要使参数自适应模型能适应不同温度的影响,需使模型内阻的调节范围大于0.02 Ω. 设计模糊控制器时,论域设计适当即可. 其它外界因素(如湿度等)对锂电池的影响相对很小,可忽略.
3 MIMO模糊控制的参数自适应模型 3.1 模型框架2.1节分析了通过调整PNGV模型的参数,能精确模拟锂电池在不同状态下的特性. 由于参数R0、 R1、 k和τ之间是高度非线性、 高耦合、 时变的,因此可采用MIMO模糊控制思想设计参数调节器[8, 9]. 基于MIMO模糊控制的参数自适应等效电路模型结构框图如图 8所示. 该模型模拟精度高、 通用性好、 辨识参数少、 简单易用.
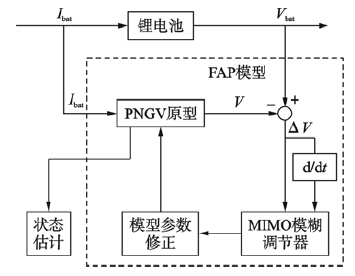 |
| 图 8 FAP模型框图Fig. 8 Block diagram of FAP model |
模型参数影响外特性; 反之,外特性的变化也必然伴随着内部参数的变化. FAP模型的设计思想是由外特性差异调节模型参量,模型中参数动态变化,随着锂电池状态变化而自适应改变,以便在SOC全区间内精确模拟锂电池内部真实状态. MIMO模糊控制器很大程度上决定了FAP模型的性能.
3.2 MIMO模糊调节器模糊控制适用于难以精确描述、 非线性、 时变的对象,鲁棒性强[16, 17]. 针对锂电池模型的特点,设计了MIMO模糊调节器,调节器结构如图 9所示.
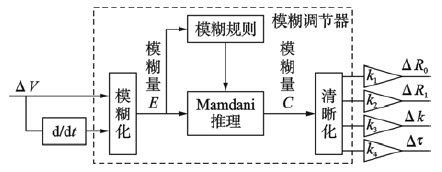 |
| 图 9 MIMO模糊调节器结构框图Fig. 9 Structured block diagram of MIMO fuzzy regulator |
为方便设计模糊规则,对实际论域放大了一定倍数,因此图 9中清晰化后需乘比例系数k1、 k2、 k3、 k4. 根据2.3节对4个参数的分析,可设计出MIMO模糊调节器. 取输入量ΔV的实际论域为[-1, 1],d(ΔV)/dt的实际论域为[-5, 5],ΔV的模糊集论域为[-4, 4],d(ΔV)/dt的模糊集论域为[-2, 2]; 取输出量R0的实际论域为[-2, 4],R1的实际论域为[-3, 4],k的实际论域为[-2, 4],τ的实际论域为[-2, 3],R0的模糊集论域为[-3, 3],R1的模糊集论域为[-1, 1],k的模糊集论域为[-1, 1],τ的模糊集论域为[-2, 2]. 模糊推理采用Mamdani取大取小合成规则,隶属函数为
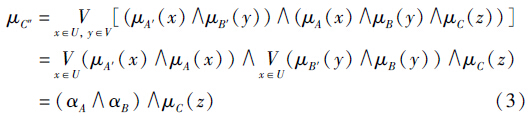
 |
| 图 10 模糊规则映射图Fig. 10 Mapping diagram of the fuzzy rules |
为对比FAP模型的控制效果,做了PNGV模型的模拟效果实验,实验结果如图 11所示. 由图 11可看出,PNGV模型在高SOC区间内模拟效果较好,误差在可接受的范围内,但随着SOC的减小,误差越来越大,在SOC约为10%处,PNGV模型模拟结果出现早衰现象,显示电池电量已经放完,误差大. 若用此模型不加优化的做SOC、 SOH估计等工作,将影响锂电池管理系统的正确性,损害电池寿命和容量.
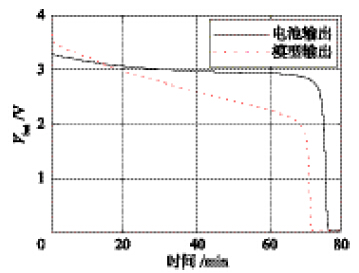 |
| 图 11 PNGV模型模拟效果Fig. 11 Simulating results of PNGV model |
导致PNGV模型估计误差逐步增大的原因主要有以下几点: ① 锂电池的内阻随电池SOC的变化而变化,固定参数的PNGV模型只能在辨识点精确模拟; ② 根据锂电池的放电性能,在电池接近耗尽时,输出电压会急剧下降,内阻会增大,而PNGV模型的参数在此时已经不再适用,最终导致估计误差很大; ③ 锂电池的时间常数直接影响电池的瞬态响应,而PNGV模型仅表征了部分时间常数,无法完全反映锂电池的瞬态响应.
4.2 参数自适应模型实验实验结果如图 12所示,相比静态参数的PNGV模型,跟踪效果明显好转,尤其在电池参数变化剧烈的低SOC区间内也能较好跟踪,但由图 12可看出,自适应模型实验结果中有个衰减点,电压瞬间跌幅稍大,这是由于电池内部参数在SOC低于一定值时,性能急剧变化所致. 下面分析各参数:
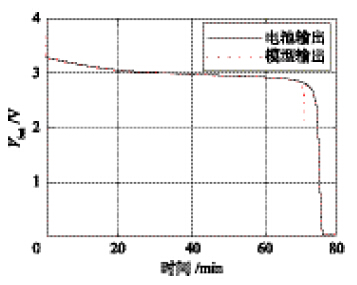 |
| 图 12 自适应调节实验效果Fig. 12 Experimental results of the adaptive parameters |
① 静态PNGV模型参数R0仅表示电池的欧姆内阻,还有其它内阻特性未表征,误差较大,而自适应R0经过调节,不仅表征电池欧姆内阻,还表征了其它内阻特性,并能反映整个SOC范围内因各种因素所引起的内阻变化; R0对电池的稳态性能有较大影响,但对于锂电池的瞬态响应影响微小.
② k表征了开路电压与负载电流的关系,能在一定程度上影响锂电池模型动态性能. 随着电池剩余电荷的不断减少,开路电压会不断变化,因此k也是变化的. 对k的自适应调节能改善模型的动态性能.
③ τ表征电路的时间常数,直接影响系统动态响应. 对τ调节,能使模型瞬态响应加快.
4.3 变工况实验为验证FAP模型的适应能力和稳定程度,做了锂电池多工况变换工作实验,实验结果如图 13所示. 从图 13可看出,FAP模型在不同工况连续变换情况下,能良好跟踪,超调很小,模拟效果好. 可见,FAP模型性能稳定,能适应复杂工况.
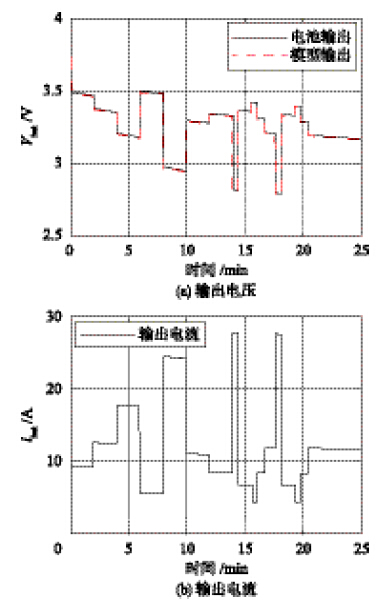 |
| 图 13 变工况实验效果Fig. 13 Experimental results under the changeable conditions |
FAP模型的基本设计原理是根据锂电池外特性反向调节模型参数,以使模型实时适应锂电池内部真实状态,提高状态估计的准确度. 为对比效果,分别对静态参数的PNGV模型和FAP模型进行了扩展卡尔曼滤波估计电池SOC实验.
安时积分法估计SOC的公式:
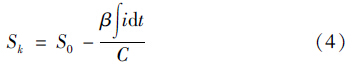
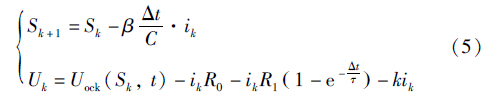
定义状态xk=[Sk],输入uk=[ik],输出yk=[Uk],那么锂电池PNGV模型的状态空间表达式为
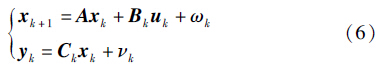
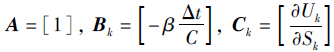 ,Bk=-βΔtC,Ck=UkSk,wk和vk是零均值高斯白噪声序列. 采用扩展卡尔曼滤波算法估计锂电池SOC,步骤如下:
,Bk=-βΔtC,Ck=UkSk,wk和vk是零均值高斯白噪声序列. 采用扩展卡尔曼滤波算法估计锂电池SOC,步骤如下: 初始化:

时间更新:

观测更新:
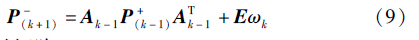
滤波增益矩阵:
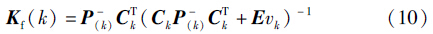
状态:

估计误差协方差:
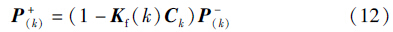
参数自适应模型和静态参数模型的扩展卡尔曼滤波(EKF)SOC估计如图 14所示,SOC估计误差如图 15所示. 从图 14、 图 15可看出,随着锂电池放电时间的延长,电池SOC不断减小,静态参数模型的估计误差不断增大,特别是在SOC较低的阶段,估计误差甚至超过了15%. 而参数自适应模型即使在较低SOC阶段仍然能控制估计误差在4%以内水平,验证了FAP模型的有效性.
 |
| 图 14 SOC估计结果Fig. 14 Estimating results of SOC |
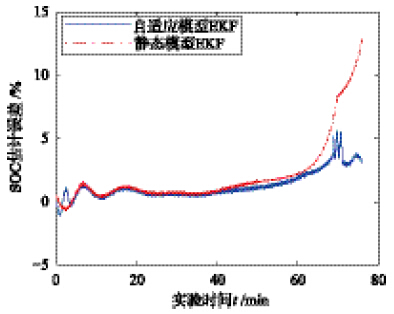 |
| 图 15 SOC估计误差Fig. 15 SOC estimation error |
基于MIMO模糊控制的锂电池参数自适应等效电路模型以PNGV模型为自适应原型,根据锂电池的特性,利用MIMO模糊调节器动态调节PNGV模型的各参数,以达到适应锂电池在不同状态、 不同环境下不同特性的目的,从而提高了锂电池SOC全区间估计精度. 实验表明,即使在SOC低于20%区间内,SOC估计误差仍能控制在4%以内,从而验证了FAP模型的有效性.
然而在锂电池自适应模型方面仍有较大研究空间. 比如,如何自适应减小锂电池老化对电池性能的影响等,这是下一步的研究内容之一.
| [1] | Sachin B, Taehyun S. Development of improved Li-ion battery model incorporating thermal and rate factor effects[C]//5th IEEE Vehicle Power and Propulsion Conference. Piscataway, NJ, USA: IEEE, 2009: 544-550. |
| [2] | Matteo C, Sergio M S. A diffusive electro-equivalent Li-ion battery model[C]//2013 IEEE International Symposium on Circuits and Systems. Piscataway, NJ, USA: IEEE, 2013: 2976-2979. |
| [3] | Zhou X, Zhang B Z, Han Z. State of charge estimation based on improved Li-ion battery model using extended Kalman filter[C]//2013 IEEE 8th Conference on Industrial Electronics and Applications. Piscataway, NJ, USA: IEEE, 2013: 607-612. |
| [4] | Chris G, Wang J B, Dave S, et al. EV/HEV Li-ion battery modelling and state of function determination[C]//21st International Symposium on Power Electronics, Electrical Drives, Automation and Motion. Piscataway, NJ, USA: IEEE, 2012: 353-358. |
| [5] | 贾玉健, 解大. 电动汽车电池等效电路模型的分类和特点[J]. 电力与能源, 2011, 32(6): 516-521. Jia Y J, Xie D. Classification and characteristics of equivalent circuit modes for EV's battery[J]. Power and Energy, 2011, 32(6): 353-358. |
| [6] | 魏学哲, 孙泽昌, 田佳卿. 锂离子动力电池参数辨识与状态估计[J]. 同济大学学报: 自然科学版, 2008, 36(2): 231-235. Wei X Z, Sun Z C, Tian J Q. Parameter identification and state estimation of Li-ion power battery in hybrid electric vehicle[J]. Journal of Tongji University: Natural Science, 2008, 36(2): 231-235. |
| [7] | 陈全世, 林成涛. 电动汽车用电池性能模型研究综述[J]. 汽车技术, 2005(3): 1-5. Chen Q S, Lin C T. Summarization of studies on performance model of batteries for electric vehicle[J]. Automobile Technology, 2005(3): 1-5. |
| [8] | 余修端, 孙秀霞, 董文瀚, 等. 基于控制性能的MIMO非线性系统动态面控制[J]. 信息与控制, 2012, 41(1): 44-60. Yu X D, Sun X X, Dong W H, et al. Dynamic surface control based on control performance for a class of MIMO nonlinear systems[J]. Information and Control, 2010, 24(8): 769-774. |
| [9] | 徐世许, 马建敏. 不确定MIMO线性系统的全局快速终端滑模控制[J]. 信息与控制, 2011, 40(5): 619-626. Xu S X, Ma J M. Global fast terminal sliding mode control of uncertain MIMO liner system[J]. Information and Control, 2011, 40(5): 619-626. |
| [10] | 石璞, 董再励. 基于EKF的AMR锂电池SOC动态估计研究[J]. 仪器仪表学报, 2006, 27(6): 1-3. Shi P, Dong Z L. EKF-based dynamic estimation of Li-ion battery SOC for AMR[J]. Chinese Journal of Scientific Instrument, 2006, 27(6): 1-3. |
| [11] | Kaypmaz T C, Tuncay R N. An advanced cell model for diagnosing faults in operation of Li-ion polymer batteries[C]//7th IEEE Vehicle Power and Propulsion Conference. Piscataway, NJ, USA: IEEE, 2011: 1-5. |
| [12] | 李哲. 纯电动汽车磷酸铁锂电池性能研究[D]. 北京: 清华大学, 2011. Li Z. Characterization research of LiFePO4 batteries for application on pure electric vehicles[D]. Beijing: Tsinghua University, 2011. |
| [13] | Thirugnanam K, Saini H, Kumar P. Mathematical modeling of Li-ion battery for charge/discharge rate and capacity fading characteristics using genetic algorithm approach[C]//2012 IEEE Transportation Electrification Conference and Expo. Piscataway, NJ, USA: IEEE, 2012: 1-6. |
| [14] | 罗玉涛, 谢斌, 何小颤. 电动汽车锂离子电池组参数辨识与SOC估计[J]. 华南理工大学学报: 自然科学版, 2012, 40(12): 79-85. Luo Y T, Xie B, He X C. Parameter identification and SOC estimation of lithium battery pack used in electric vehicles[J]. Journal of South China University of Technology: Natural Science Edition, 2012, 40(12): 79-85. |
| [15] | Gao W G, Jiang M, Hou Y M. Research on PNGV model parameter identification of LiFePO4 Li-ion battery based on FMRLS[C]//2011 6th IEEE Conference on Industrial Electronics and Applications. Piscataway, NJ, USA: IEEE, 2011: 2294-2297. |
| [16] | 张广辉, 苏成利, 李平. 基于偏格式线性化的MIMO系统无模型自适应控制[J]. 信息与控制, 2011, 40(3): 338-342. Zhang G H, Su C L, Li P. Model-free adaptive control of MIMO systems based on linearization of partial format[J]. Information and Control, 2011, 40(3): 338-342. |



