2. 吉首大学信息科学与工程学院, 湖南 吉首 416000
2. College of Information Science and Engineering, Jishou University, Jishou 416000, China
1 引言
人类具有从当前感知的事物联想起另一个相关事物的能力，能从破碎的信息中整理出完整的信息，这种联想记忆的能力是人类认知世界和改造世界的重要手段. 然而如何使计算机拥有人脑一样的联想记忆能力成为中外学者的研究热点，在计算机模拟人类联想记忆的研究中，人工神经网络应运而生. 自Kosko提出了经典的联想记忆(associative memories，AM)[1]，掀起了联想记忆神经网络的研究热潮，Hopfield于1982年提出了著名的Hopfield联想记忆网络模型，但这种联想记忆神经网络的性能有限，在众多应用领域都受到了很大程度的限制. 基于此，不少学者对联想记忆神经网络的性能改进做出了深入研究[2, 3, 4, 5, 6, 7, 8, 9]，Kosko在改变网络结构基础上提出了双向联想记忆(bidirectional associative memories，BAM)[2]，Ritter等人结合数学形态学与联想记忆神经网络，通过引入实数环(R，∨，∧，+)提出了形态学联想记忆(morphological associative memories，MAM)[3]，随即又提出了形态学双向联想记忆(morphological bidirectional associative memories，MBAM)[4]，使联想记忆网络性能得到了很大提升，特别是自联想在无噪声的情况下表现出无限存储能力. 王士同等运用模糊运算基于实数环(R+，∨，∧，×)，(R+∈(0，∞))提出了模糊形态学联想记忆网络(fuzzy morphological associative memories，FMAM)[5]，更有学者建立了形态学联想记忆神经网络框架[10].
这些神经网络的研究都是基于实数域内的，然而在信号处理过程中为了分析与计算方便，将信号转换到复数域进行处理，复数域内神经网络应运而生[11, 12, 13, 14, 15, 16, 17]. 文[11]提出了复形态联想记忆神经网络模型，可直接处理复信号，但只分析了单向形态学联想记忆模型的相关性能. 目前复域内神经网络的理论分析、 模型设计和应用已引起学者们的广泛关注[12, 13, 14, 15, 16, 17]. 在理论分析方面，Xu等研究了混合时滞复值神经网络的动态特性[12]，Zhang等分析了复值神经网络平衡点存在性、 唯一性和全局渐近稳定性的充分条件[13]，Valle探讨了复值神经网络记忆向量反演的充分条件[14]； 在网络模型设计方面，Zheng设计了一类基于复值矩阵分解的阈值复值神经联想记忆网络[15]； 在复值神经网络应用方面，Terabayashi等将复值神经网络应用于超宽带波达方位估计[16]，Ding等将复值神经网络应用于衰落信道预测[17]，获得了较传统预测方法更高的精确度.
本文在文[4]和文[11]的基础上提出复形态双向联想记忆网络(complex morphological bidirectional associative memory，CMBAM). 本文研究的复形态双向联想记忆网络与文[11]研究的复形态联想记忆网络的拓扑结构不同，因此本文的工作并不是文[11]的重复，而是进一步的推广和深入，对复形态双向联想记忆网络的性质和性能进行了首次分析和研究.
2 相关定义及说明经典及各种改进型形态学联想记忆网络都是基于完全格进行运算的，在此首先介绍复形态双向联想记忆网络的相关数学基础.
偏序关系的定义[18] 设R是集合A上的一个二元关系，若R满足：
ⅰ自反性： 对任意x∈A，有xRx.
ⅱ反对称性： 对任意x，y∈A，若xRy且yRx，则x=y.
ⅲ传递性： 对任意x，y，z∈A，若xRy且yRz，则xRz，
称R为A上的偏序关系，通常记作“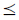
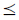”，并用ab表示(a，b)∈R.
在此基础上本文先定义复数域上的偏序关系，然后通过定义格和环来构造复形态双向联想记忆网络的联想记忆规则.
定义1(复数域C内的偏序关系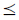′)[11] 设a，b∈C，其中a=x+iy，b=u+iv(i2=1)，x，y，u，v∈R，如果满足下列两个条件之一：
① x≤u
② x=u and y≤v
则称a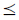′b，显然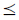′是复数域C上的偏序关系，并记此偏序关系为(C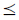，′)，容易证明该偏序关系为顺序集.
定义2(复数域C内的偏序关系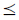″)[11] 设a，b∈C，其中a=x+iy，b=u+iv(i2=1)，x，y，u，v∈R，如果同时满足x≤u，y≤v，则称a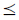″b，同样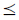″也是复数域C上的偏序关系，并记此偏序关系为(C，″).
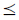格的定义[18] 设(A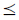，)是一个偏序集，若A中任意两个元素a，b构成的集合都有最大下界(下确界)和最小上界(上确界)则称(A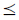，)为一个格.
从前面的定义可知(C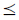，′)满足格定义的条件，故(C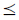，′)可以做成一个关于偏序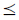′的格. 格中的最大下界和最小上界分别用a∧′b和a∨′b表示，将∧′、 ∨′两个运算符当作是格(C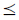，′)中的两个二元运算，然后将代数和“+”运算导入格中便得到复数域中的环结构(C，∨′，∧′，+)； 同理可得到(C，∨″，∧″，+)环结构，现将两种环结构统一记为(C，∨，∧，+).
对于矩阵Am×p和矩阵Bp×n，最大积矩阵Cm×n=Am×p
Bp×n，此处，
和分别表示复合算子(∧，+)和(∨，+)，其中Cm×n的元素cij(i=1，…，m； j=1，…，n)为
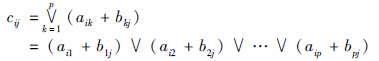
Bp×n：
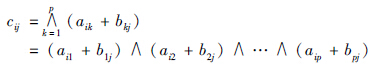
复形态双向联想记忆网络是基于复数环(C，∨，∧，+)基础之上，该神经网络处理的信号可以从两个方向进行输入和输出. 设xξ=(xξ1，…，xξn)′∈Cn，yξ=(yξ1，…，yξm)′∈Cm，其中(xξ)′表示(xξ)的转置，从X→Y方向的复形态双向联想记忆网络的连接权矩阵定义如下：
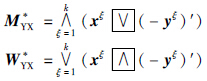
定义3 当AX=Y，矩阵A=(aij)m×n称为(X，Y)的完全回忆记忆； 当AX=Y，矩阵A=(aij)m×n称为(X，Y)的完全回忆记忆.
定理1
(Ⅰ) MXYxξ=yξ，
ξ=1，…，k，对于每行i=1，…，m和每个模式ξ∈｛1，…，k｝，存在一个列jiξ∈｛1，…，n｝使得miji*ξ=yξi-xξji*ξ，其中jiξ取决于i和ξ.
(Ⅱ) WXYxξ=yξ，ξ=1，…，k，对于每行i=1，…，m和每个模式ξ∈｛1，…，k｝，存在一个列jiξ∈｛1，…，n｝使得wijiξ=yξi-xξjiξ.
证明
(Ⅰ) 先证其充分性，设MXYxξ=yξ，ξ=1，…，k，任取i∈｛1，…，m｝和γ∈｛1，…，k｝，需要证明存在一个列j0∈｛1，…，n｝使得mij0=yγi-xγj0. 假设mij≠yγi-xγj，j=1，…，n. 由于MXY是矩阵yξ(-xξ)′的最大值，故yξ(-xξ)′≤MXY. 则假设等价于mij>yγi-xγj，j=1，…，n.
而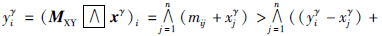
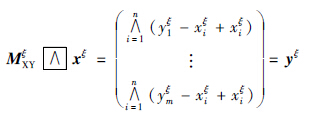
+xγj)>∧nj=1((yγi-xγj)+xγj)=yγi，与假设矛盾，故等式mij=yγi-xγj成立. 下面证其必要性，设mij=yγi-xγj，j=1，…，n，由于yξ(-xξ)′=MξXY≤MXY，ξ=1，…，k，故MξXYxξ≤MXYxξ.
xξ.
据上，要证得MXYxξ=yξ，ξ=1，…，k必须证明MXYxξ≤yξ. 现取任意i∈｛1，…，m｝和γ∈｛1，…，k｝，有：
xγ≤yγ. 所以MXYxξ=yξ，ξ=1，…，k成立. (Ⅱ)类似(Ⅰ)的证明，证毕.
推论1
(Ⅰ) MXYxξ=yξ，ξ=1，…，k，对于每个行i=1，…，m和每个模式ξ∈｛1，…，k｝存在一个列jiγ∈｛1，…，n｝使得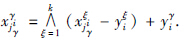
(Ⅱ) WXYxξ=yξ，ξ=1，…，k，对于每个行i=1，…，m和每个模式ξ∈｛1，…，k｝存在一个列jiγ∈｛1，…，n｝使得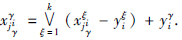
定理2
(Ⅰ) M*YXyξ=xξ，ξ=1，…，k，对于每个行i=1，…，n和每个模式ξ∈｛1，…，k｝存在一个列jiξ∈｛1，…，m｝使得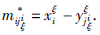
(Ⅱ) W*YXyξ=xξ，ξ=1，…，k，对于每个行i=1，…，m和每个模式ξ∈｛1，…，k｝存在一个列jiξ∈｛1，…，m｝使得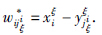
证明 类似定理1的证明.
推论2
(Ⅰ) M*YXyξ=xξ，ξ=1，…，k，对于每个行i=1，…，m和每个模式ξ∈｛1，…，k｝存在一个列jiγ∈｛1，…，n｝使得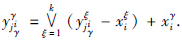
(Ⅱ) W*YXyξ=xξ，ξ=1，…，k，对于每个行i=1，…，m和每个模式ξ∈｛1，…，k｝存在一个列jiγ∈｛1，…，n｝使得
定理1、 2和推论1、 2给出了一个模式能够完整回想与否的简单有效的计算方法； 根据这些方法，对于任意模式的连接权矩阵存在一个元素满足所给定的等式，就能可靠回想. 其中定理1和推论1是针对X→Y方向的复形态双向联想记忆网络的完整回想； 定理2和推论2是针对Y→X方向的复形态双向联想记忆网络的完整回想. 当输入模式与输出模式相同即X=Y时，即为自联想记忆网络，对于自联想记忆网络定理1、 2和推论1、 2也成立.
定理3 当同时满足下列两个条件时，有：
① 对任意的r∈｛1，…，k｝和i=1，…，m，存在这样一个jir∈｛1，…，n｝使得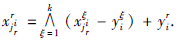
② 对任意的r∈｛1，…，k｝和j=1，…，n，存在这样一个ijr∈｛1，…，m｝使得
证明 根据推论1，则条件①中蕴含MXYxξ=yξ，ξ=1，…，k. 同理，根据推论2，则条件②中蕴含M*YXyξ=xξ，ξ=1，…，k.
因此
定理4 当同时满足下列两个条件时，有:
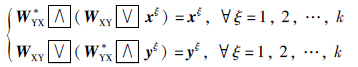
(Ⅰ) 对任意的r∈｛1，…，k｝和i=1，…，m，存在这样一个jir∈｛1，…，n｝使得
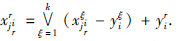
(Ⅱ) 对任意的r∈｛1，…，k｝和j=1，…，n，存在这样一个ijr∈｛1，…，m｝使得
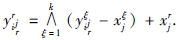
证明 类似定理3的证明.
复形态双向联想记忆网是一种具有反馈的非线性动力系统，这种网络的状态按迭代规律演化，对于信息的处理是一个由输入反复迭代而演化到其平衡态的过程. 定理3和定理4给出了复形态双向联想记忆网络完全联想记忆的条件，当满足定理3和定理4的条件时，复形态双向联想记忆网络具有稳定的状态，而且迭代一步就能可靠回想所存储的模式.
3.2 复形态双向联想记忆网络的抗噪声能力分析
噪声普遍存在于主观和客观世界中，本文将含噪声的模式统称为受损模式. 在构建神经网络时，由于采集设备的精度限制，训练数据获取方法的局限性，为顾及模式对之间的相容性、 矛盾性等对训练模式对进行微调以及为适应环境变化等多种因素对训练模式对进行微调等均可使模式受损. 文中将xγ的受损模式记为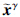
γ，即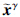≠xγ. 当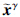≥xγ时称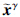只含有膨胀噪声； 当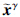≤xγ时称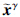只含有腐蚀噪声，类似定义
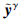. 下面分别输入xγ、 yγ的受损模式，分析复形态双向联想记忆网络的抗噪能力.
定理5
(Ⅰ) 设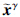为xγ的含噪模式，γ=1，…，k，那么MXY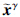=yγ，当且仅当：
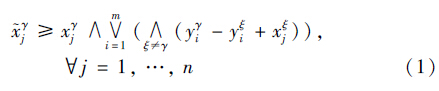
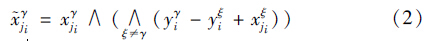
(Ⅱ) 设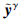为yγ的含噪模式，r=1，2，…，k，那么M*YX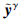=xγ，当且仅当：
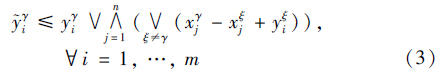
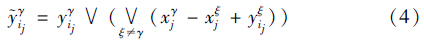
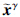=yγ，有：
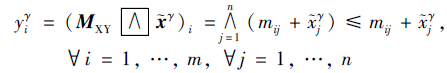
对于不等式(5)假设存在这样一个行i∈｛1，…，m｝使得：
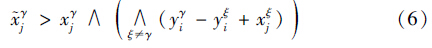
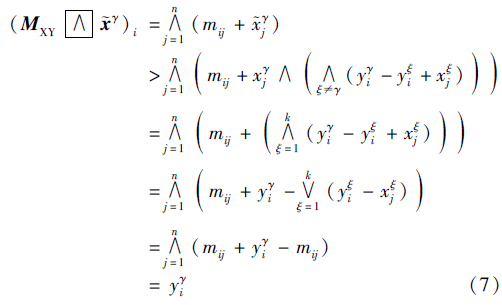
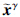)i>yγi，与假设(M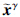)i=yγi矛盾. 因此对于每一行i必须存在一个列ji使之满足式(2). 下面证明其充分性，设：
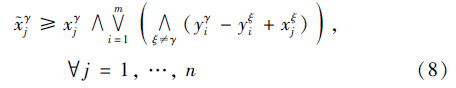
当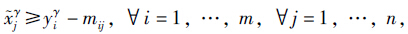
由上部分证明过程可知式(8)成立，则:
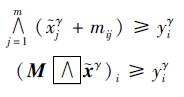
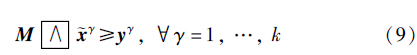
因此，如果能证明对γ=1，…，k有M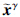≤yγ，那么就有M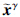=yγ，γ=1，…，k. 现在任选γ∈｛1，…，k｝和i∈｛1，…，m｝，则：
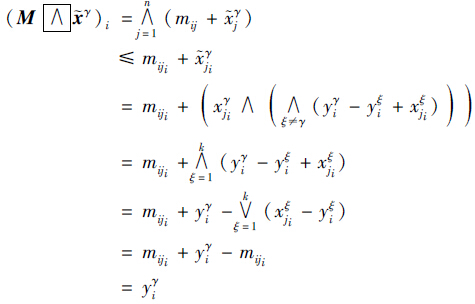
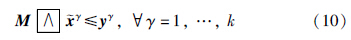
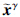=yγ，γ=1，…，k. 同理可证该定理中的(Ⅱ)，证毕.
定理5表明，复形态双向联想记忆网络对从X端激发的单一膨胀噪声具有较强的稳健性； 复形态双向联想记忆网络对从Y端激发的单一腐蚀噪声具有较强的稳健性.
定理6
(Ⅰ) 设γ为xγ的含噪模式，γ=1，…，k，有WXY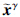=yγ，当且仅当
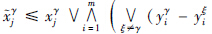+xξj)，j=1，…，n并且，对于每一个行i∈｛1，…，m｝，存在这样一个列ji∈｛1，…，n｝使得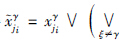
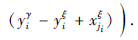
(Ⅱ) 设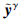为yγ的含噪模式，γ=1，2，…，k，有W*YX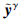=xγ，当且仅当
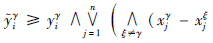+yξi)，i=1，…，m,并且，对于每一个行j∈｛1，2，…，n｝，存在这样一个列ij∈｛1，2，…，m｝使得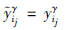
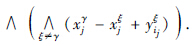
定理6表明，复形态双向联想记忆网络对从X端激发的单一腐蚀噪声具有较强的抵抗能力； 复形态双向联想记忆网络对从Y端激发的单一膨胀噪声具有较强的抵抗能力.
3.3 复形态双向自联想记忆网络的存储性能和稳定性分析
定理7 复形态双向自联想记忆网络有： WXXX=X，MXXX=X.
证明 对i=｛1，…，m｝和ξ=1，…，k有：
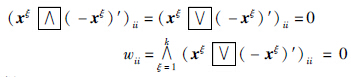
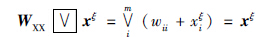
完全回忆记忆，即WXXX=X成立，同理可证MXXX=X. 定理7中复形态双向自联想记忆网络对于模式X的类型、 维数以及模式对数目没有任何限制，记忆矩阵WXX和MXX对于任意输入模式xξ都是稳定的，表明自联想复形态双向联想记忆网络具有无限存储能力，特别在无噪声情况下能保证完全回忆.
定理8 若WXXZ=V，MXXΖ=U则WXXV=V，MXXU=U.
证明 设WXXZ=V. 由于wii=0，i=1，…，n，有：
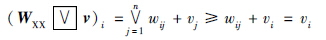
设i，j，l∈｛1，…，n｝. 对γ=1，…，k有：
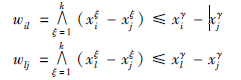
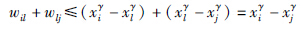
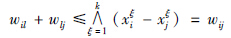
根据式WXXZ=V，对于i=1，…，n有:
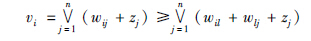
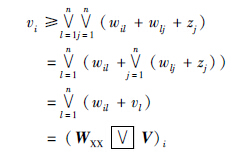
由式(11)和式(12)可得WXXV=V，同理可得MXXU=U.
从定理8可以看出，复形态双向自联想记忆网络像人类一样具备联想记忆的能力，一旦初始模式Z能被复形态双向联想记忆网络有效记忆，则该模式输入复形态双向联想记忆网络时，神经网络就能进入稳态，能被一步完全再现，即对于任意输入模式Z神经网络能一步收敛.
特别地，当复数虚部取0时即为实数，因此复形态双向联想记忆网络包括了复形态双向联想记忆网络，且与实形态双向联想记忆网络[2]有相似的定理和相关性质，实数域形态双向联想记忆网络只是复数域形态双向联想记忆网络的特例.
4 仿真实验本次实验随机选取字母表中的(A，a)，(B，b)，(G，g)，(M，m)和(R，r)5个字母模式对图片进行仿真. 读取大小为32×32的字母图片，对其进行归一化处理，按照行扫描的方式对图像矩阵进行扫描使其转变成1 024×1的列向量，然后采用快速傅里叶变换(FFT)变换成一个1 024×1的复向量，根据连接权矩阵计算公式以及复域内的偏序关系计算神经网络的连接权矩阵，输入其它模式对，按照以上方法进行一系列变换后，对待识别模式进行识别得到输出复矩阵，对输出复矩阵进行快速傅里叶逆变换(IFFT)变换后再将其还原成32×32矩阵形式，最终将其结果显示出来.
 |
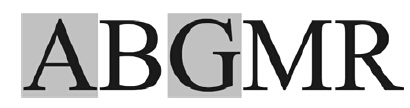| 图 1 X→Y方向的CMBAM的输入模式Fig. 1 The input patterns of CMBAM from X to Y |
 |
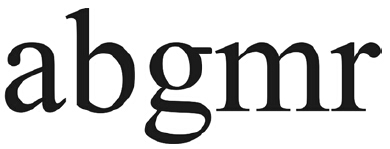| 图 2 X→Y方向的CMBAM的输出模式及Y→X方向的CMBAM的输入模式Fig. 2 The output patterns of CMBAM from X to Y and the input patterns of CMBAM from Y to X |
 |
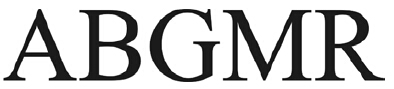| 图 3 Y→X方向的CMBAM的输出模式Fig. 3 The output patterns of CMBAM from Y to X |
给字母A和G加入10％的随机噪声，神经网络仍能正确识别，仿真结果表明复形态双向联想记忆网络能实现完全联想记忆，能抵抗一定范围内的随机抗噪声，同时也验证了定理7和定理8的正确性.
5 结束语本文研究的复形态双向联想记忆神经网络可以直接处理复信号，给出了神经网络能否实现双向完全联想的计算方法. 本文对复形态双向自联想记忆神经网络的稳定性、收敛性和存储能力及神经网络的抗噪声能力的分析，为研究其它类型的复联想记忆网络提供了参考.
| [1] | Kosko B. Associative memory: A system-theoretical approach[M]. Berlin, Germany: Springer-Verlag, 1977. |
| [2] | Kosko B. Bi-directional associative memory[J]. IEEE Transactions on System, Man and Cybernetics, 1988, 18(1): 49-60. |
| [3] | Ritter G X, Sussner P. Morphological associative memories[J]. IEEE Transactions on Neural Network, 1998, 9(2): 281-292. |
| [4] | Ritter G X, Diaz de Leon J L, Sussner P. Morphological bidirectional associative memories[J]. IEEE Transactions on Neural Network, 1998, 12(6): 851-867. |
| [5] | Wang S T, Lu H J. On new fuzzy morphological associative memories[J]. IEEE Transactions on Fuzzy Systems, 2004, 12(3): 316-323. |
| [6] | Valle M E, Sussner P. A general framework for fuzzy morphological associative memories[J]. Fuzzy Sets and Systems, 2008, 159(7): 747-768. |
| [7] | 曾水玲, 徐蔚鸿, 杨靖宇. 模糊形态学双向联想记忆网络的性质[J]. 模式识别与人工智能, 2012, 25(1): 54-62. Zeng S L, Xu W H, Yang J Y. Properties of fuzzy morphological bidirectional associative memories[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(1): 54-62. |
| [8] | 关焕新, 古占山, 张化光. 不确定双向联想记忆神经网络的稳定性分析[J]. 控制理论与应用, 2008, 25(3): 421-426. Guan H X, Gu Z S, Zhang H G. Stability analysis of uncertain bi-directional associative memory neural networks with variable delays[J]. Control Theory and Applications, 2008, 25(3): 421-426. |
| [9] | Valle M E, Sussner P. Storage and recall capabilities of fuzzy morphological associative memories with adjunction-based learning[J]. Neural Network, 2011, 24(1): 75-90. |
| [10] | 冯乃勤, 刘春红, 张聪品, 等. 形态学联想记忆框架研究[J]. 计算机学报, 2010, 33(1): 157-166. Feng N Q, Liu C H, Zhang C P, et al. Research on the framework of morphological associative memories[J]. Chinese Journal of Computers, 2010, 33(1): 157-166. |
| [11] | 陈松灿, 刘伟龙. 复形态联想记忆及其性能分析[J]. 软件学报, 2002, 13(3): 453-459Chen S C, Liu W L. Complex morphological associative memories and their performance analysis[J]. Journal of Software, 2002, 13(3): 453-459. |
| [12] | Xu X H, Zhang J Y, Shi J Z. Exponential stability of complex-valued neural networks with mixed delays[J]. Neurocomputing, 2014, 128(3): 483-490. |
| [13] | Zhang Z Y, Lin C, Chen B. Global stability criterion for delayed complex-valued recurrent neural networks[J]. Networks and Learning Systems, 2014, 25(9): 1704-1708. |
| [14] | Valle M E. Complex-valued recurrent correlation neural networks[J]. IEEE Transactions on Networks and Learning Systems, 2014, 25(9): 1600-1612. |
| [15] | Zheng P S. Threshold complex-valued neural associative memory[J]. IEEE Transactions on Networks and Learning Systems, 2014, 25(9): 1714-1718. |
| [16] | Terabayashi K, Natsuaki R, Hirose A. Ultrawideband direction-of-arrival estimation using complex-valued spatiotemporal neural networks[J]. IEEE Transactions on Networks and Learning Systems, 2014, 25(9): 1727-1732. |
| [17] | Ding T B, Hirose A. Fading channel prediction based on combination of complex-valued neural networks and chirp Z-transform[J]. IEEE Transactions on Networks and Learning Systems, 2014, 25(9): 1686-1695. |
| [18] | 李峰, 王高丽, 苏厚勤. 离散数学[M]. 北京: 清华大学出版社, 2011: 22-110. Li F, Wang G L, Su H Q. Discrete mathematics[M]. Beijing: Tsinghua University Press, 2011: 22-110. |