1 引言
在图像测量和机器视觉领域，摄像机标定是指根据摄像机模型求取摄像机内外参数的过程，是由2维图像获取3维信息的基本步骤，被广泛应用于3维重建、 视觉检测和监控等领域[1]. 在现有摄像机标定方法中，基于黑白棋盘图像的平面模板标定方法因模板制作简单且算法成熟而被广泛应用[2]. 由于摄像机标定精度在很大程度上取决于标定模板角点的定位精度，因此如何确定标定模板角点位置是机器视觉领域的重要研究课题[3,4,5,6,7,8,9,10,11,12].
在摄像机标定实验中，棋盘图像往往复杂背景，为减少背景对棋盘图像角点检测的影响，目前常采用鼠标点击式人机交互方法对棋盘图像角点进行检测[3]. 该方法需先用鼠标按一定顺序点击图像外围4个点以确定出角点位置的参考范围，然后再通过角点检测算法检测出点击范围内角点的位置. 该方法费时费力，难以实现摄像机标定过程的自动化. 另一些研究关注于如何改进传统角点检测方法以解决棋盘图像角点检测问题，而对具有复杂背景棋盘图像的角点提取问题研究较少[4,5,6]. 目前，已提出一些棋盘图像角点自动提取方法[7,8,9,10,11]. 文[7]采用hough变换通过提取图像直线特征检测棋盘图像角点，实现棋盘图像特征点的自动提取以提高摄像机标定效率； 文[11]提出一种基于灰度差异的棋盘图像角点自动检测方法，利用一种圆形角点检测器，在无需对棋盘格图像进行预处理的情况下，可检测具有一定噪声或较模糊棋盘图像的角点. 总的来说，与摄像机标定方法相比，棋盘图像角点自动检测和提取方法的研究依然较少，且缺乏通用的方法框架. 这种情况在一定程度上阻碍了摄像机标定过程自动化程度的提高. 为此，本文提出一种新的基于对称性分析的棋盘图像角点检测方法. 该方法将棋盘图像角点检测问题转化为图像特征点的对称性分析问题. 实验结果表明，本文提出的方法具有较高的角点检测准确度和精度，可实现棋盘图像角点的自动检测，适用于摄像机标定.
2 特征点检测本文提出的棋盘图像角点检测方法主要包括图像预处理、 候选特征点检测、 特征点提取、 初始角点检测、 角点提取和亚像素角点检测等步骤，其相互关系如图 1所示. 其中，在图像预处理部分，首先对棋盘图像进行高斯滤波以减少噪声影响，然后对滤波后的图像采用Canny算子进行边缘检测. 本文采用的滤波函数如式(1)所示：
 |
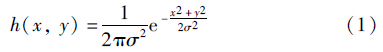
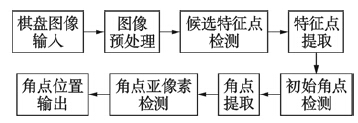| 图 1 提出的角点检测方法框图Fig. 1 The block diagram of the proposed corner detection method |
为检测棋盘图像角点，经图像预处理后，本文首先定义并检测棋盘图像特征点，然后提取满足对称性要求的特征点为图像角点. 其中，棋盘图像特征点是指与棋盘图像角点具有相同或类似像素对称性的图像点. 假设棋盘图像u的特征点集合为Pf，角点集合为Pc，则角点集合可看作特征点集合的子集，即Pc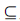
Pf. 假设u0为u的边缘图像，定义图像候选特征点集Pfd为在其邻域内有4条图像边缘交汇的图像点集合，且有Pf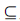Pfd. 通过上述定义，棋盘图像角点检测问题转换为根据u求Pfd，由Pfd提取Pf，进而根据Pf求Pc的问题.
由于图像特征点集Pf为Pfd的子集，因此需首先求取Pfd. 根据Pfd定义，可通过设置以u中每个图像点为中心，大小为w×w的滑动窗口遍历u0，若滑动窗口边框与u0中的边缘有4个交点则将该图像点设置为候选特征点，其求取过程如图 2所示. 图 2(a)为棋盘图像u，图 2(b)为边缘图像u0，图 2(c)为候选特征点集Pfd，其中候选特征点置1，非候选特征点置0.
 |
| 图 2 候选特征点提取Fig. 2 Extraction of candidate feature points |
由图 2(c)可见，Pfd中的候选特征点大多相互连接，形成连通区域. 而由图 2(a)可见，棋盘图像角点一般具有较好的像素对称性. 根据Pf定义和PfPfd，可通过求取Pfd中具有较高像素对称性的候选特征点得到Pf. 为此，本文首先对Pfd进行聚类，然后通过求取每个聚类中具有最高像素对称性的图像点作为特征点以获得Pf.
实现Pfd聚类的方法很多，本文采用连通域分析的方法对Pfd进行聚类. 在该方法中，首先对Pfd中的候选特征点进行标记[12,13]，赋相邻候选特征点相同标号，并将具有相同标号的候选特征点视为Pfd的一个连通域； 然后通过设置最大连通域距离，对具有不同标号的连通域进行合并； 最后将合并后的每个连通域看作Pfd的一个聚类，从而实现对Pfd的聚类. 本文进行候选特征点标记的主要步骤如下：
(1) 对候选特征点图像按从上到下、 从左到右的顺序进行搜索，若搜索到的候选特征点未进行标记，则赋该候
选特征点新的标号； 以新标记的候选特征点为起始点进行8邻域搜索，若在其8邻域内搜索到未标记的候选特征点，则为搜索到的未标记候选特征点赋相同标号，并以新标记的候选特征点为起始点继续进行8邻域搜索； 若在8邻域内未搜索到未标记的候选特征点，则结束该次搜索.
(2) 采用步骤(1)对候选特征点图像中所有未标记候选特征点进行标记，直到完成所有候选特征点标记为止.
由上述标记过程可见，只需对候选特征点图像进行一次扫描即可完成所有候选特征点的标记. 将具有相同标号的候选特征点作为一个连通域，通过设置最大连通域距离dcd，可实现不同连通域的合并，其步骤如下：
(1) 假设候选特征点pcf∈Pfd为连通域c1的边缘点，即在Pcf的8邻域范围内存在非候选特征点，若Pcf在图像中的坐标为[h，l]，则在[h-dcd： h+dcd，l-dcd： l+dcd]范围内搜索除c1外的其它连通域，若在搜索范围内搜索到其它连通域c2，则将c1和c2合并为一个连通域. >
(2) 采用步骤(1)对所有连通距离小于dcd的连通域进行合并.
在上述连通域合并方法中，一般dcd取dcd≥2. 显然，dcd取值越大，得到的候选特征点聚类个数越少，后续角点检测越简单，但较大的dcd可能会造成检测到的特征点中角点的丢失.
假设通过图像标注和连通域合并将Pfd分割为N个候选特征点聚类｛s1，s2，…，sN｝，假设聚类si中含有m个候选特征点｛d1，d2，…，dm｝，特征点提取的主要思想是通过计算si中每个候选特征点的对称性，选择其中具有最高对称性的候选特征点作为si对应的特征点fi∈Pf，即：
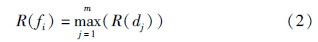
目前已提出多种有效的角点检测算法[14,15,16]，但可用于度量图像点对称性的算法较少. 为计算R(dj)，本文采用Bennett和Lasenby提出的ChESS算子计算候选特征点的对称性[17]. ChESS算子是一种专门针对棋盘图像设计的特征点检测算子，其主要思想是通过度量图像点对称性以检测棋盘图像角点. 研究结果表明[17]，该算子能有效度量包括棋盘图像角点在内的图像点的对称性. 采用ChESS算子计算R(dj)主要包括图像点采样和对称响应计算两个步骤.
(1) 图像点采样： 设置采样半径为r，采样点个数为n，以候选特征点dj为中心，在棋盘图像u中选取采样点集I=｛I1，I2，…，In｝，其采样过程如图 3所示. 图中给出采样半径分别为r=3和r=5，采样个数n=16时，采样中心点0与采样点间的关系. 一般采样点个数n取4的倍数以便计算.
 |
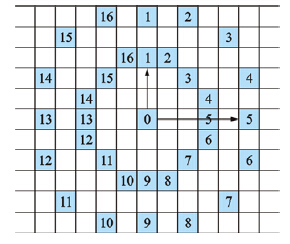| 图 3 采样点选择Fig. 3 Sample points chosen |
(2) 对称响应计算： 根据采样点集I计算dj对称性响应为
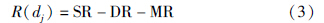
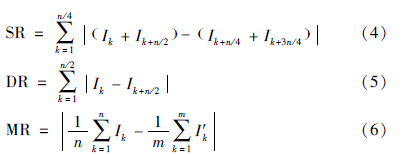
根据上述过程，可计算dj的对称响应值. 当dj满足式(2)且R(dj)>0时，取dj为棋盘图像特征点，即dj=fi∈Pf. 通过计算Pfd中每个聚类所对应的图像特征点，可得到特征点集Pf，从而实现棋盘图像u的特征点提取. 采用ChESS算子，根据图 2(c)所示的Pfd得到的Pf如图 4所示.
 |
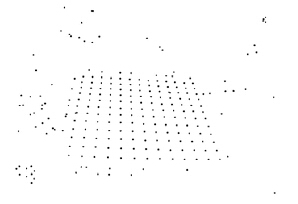| 图 4 特征点提取Fig. 4 Extraction of feature points |
由于特征点集Pf既包括角点也包括非角点，即Pf=Pc∪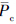
，如何从Pf中区分Pc和c是角点检测的关键. 显然，Pc与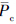相比，Pc具有明显的对称性. 对称性分析是区分Pc与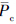的有效途径. 由于无法确切知道哪些特征点为角点，为从Pf中提取Pc，本文采取先部分后整体的角点检测策略. 该方法首先提取Pf中满足对称性要求的初始角点，然后以初始角点为起始点根据对称性检测其它角点.
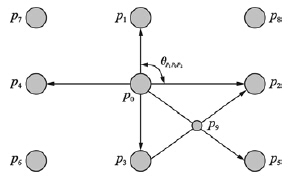
为确定角点检测起始点，本文定义初始角点为Pf中满足对称性要求的任意9个相邻特征点，其对称关系如图 5所示. 在图中，中心特征点为po，相邻特征点分别为p1～p8. 其中，p1～p4为距离po最近的4个特征点，称为临近特征点； p5～p8为po对角线方向的特征点，称为对角特征点. Pf中相邻的任意9个特征点是否为初始角点需从3方面进行判断，即临近特征点对称性、 对角特征点对称性和临近特征点夹角范围.
 |
| 图 5 初始角点Fig. 5 Initial corner points |
假设特征点po～p8坐标分别为(xi，yi)，0≤i≤8，若在位置误差范围内临近特征点p1～p4与po坐标满足如下关系：
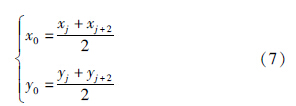
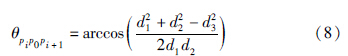
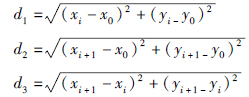
假设对角特征点为pk，5≤k≤8，其相邻的临近特征点分别为pi和pj，1≤i，j≤4，若在位置误差范围内pk坐标与pi和pj及po坐标间满足：
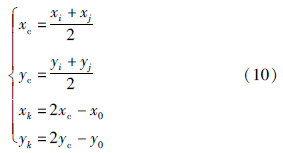
通过判断Pf中任意相邻9个特征点是否满足临近特征点对称性、 对角特征点对称性和临近特征点夹角范围要求，可实现初始角点检测，且检测到的角点为棋盘图像相邻3个角点行中的连续角点.
3.2 角点提取由于摄像机标定所用棋盘图像每行和每列所含的角点个数确定，根据角点对称性，以初始角点为搜索起始点，可实现其它角点位置估计. 假设棋盘图像每行的角点个数为Hc，每列角点个数为Lc，若检测到的一行角点中所含角点的个数为Hc，则称该角点行为正常角点行，否则称该角点行为非正常角点行.
为从Pf中提取Pc，本文首先根据已知角点估计其它角点位置，然后将所估计角点位置处的特征点设为角点. 由已知角点估计其它角点位置一般包括以下3种情况： (1) 已知角点行中2个及2个以上连续角点(如初始角点)，估计该行中其它的角点； (2) 根据两个相邻非正常角点行估计其它角点行； (3) 已知两个相邻正常角点行估计其它角点行.
针对第1种情况，本文采用的角点位置估计方法如图 6(a)所示. 其中，p1和p2分别表示角点行中的两个相邻角点. 根据对称性，可分别估计出p1关于p2的对称点P3和p2关于P1的对称点P4的位置. 在位置估计误差范围内，提取Pf中P3和P4位置处的特征点作为该行角点. 依次采用该方法，可检测出角点行中的所有角点. 针对第2种情况，本文采用的角点位置估计方法如图 6(b)所示，其中，p1、 P2和P3为某角点行中3个相邻角点，p4和po分别为相邻角点行中的角点，p5～P10为根据对称性估计出的新角点行中角点位置. 在位置误差范围内，将Pf在p5～P10位置处的特征点置为角点，然后分别以p5～p7和p8～p10为起始点，采用图 6(a)所示方法检测出新角点行中的其它角点. 针对第3种情况，本文采用的角点位置估计方法如图 6(c)所示. 假设p11、 P12和P13为正常角点行1中的角点，P21、 P22和p23为正常角点行2中的角点，则根据对称性可分别估计出相邻角点行0和角点行3中角点位置. 在位置误差范围内，将Pf中相应位置的特征点置为角点. 根据上述方法可根据初始角点实现棋盘图像角点检测.
 |
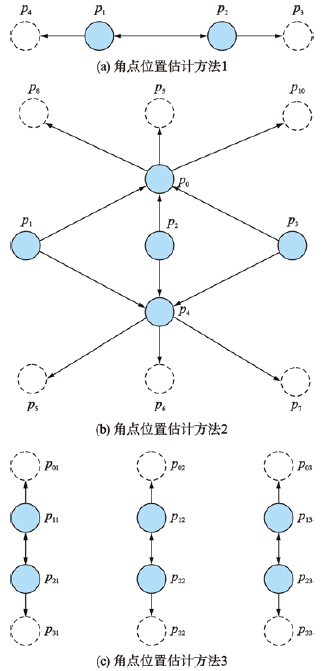| 图 6 角点位置估计Fig. 6 Corner location estimation |
在上述3种情况中，涉及根据2个相邻角点估计其它角点位置的问题. 假设任意两个相邻角点pi和pj坐标分别为(xi，yi)、 (xj，yj)，则pi关于pj对称角点psi=(xsi，ysj)和pj关于pi的对称角点psj=(xsj，ysj)可分别表示为
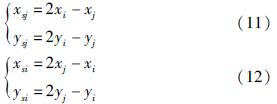
根据式(11)和式(12)可估计任意两个相邻角点的对称角点位置.
3.3 亚像素角点检测目前，针对图像亚像素检测[18]问题已提出了一些方法. 为提高棋盘图像角点检测精度，本文采用Bouguet在摄像机标定工具箱[3]中的方法进行角点亚像素检测. 该方法以检测到的角点位置为初值，通过设置检测窗口，对窗口内的像素进行线性插值，然后采用Forstner算子进行角点亚像素检测[3].
综上所述，本文提出的棋盘图像角点检测方法的主要步骤如下：
(1) 图像预处理. 对棋盘图像u进行高斯滤波，采用Canny算子求边缘图像uo.
(2) 候选特征点检测. 设置滑动窗口，根据角点与u0间的关系求候选特征点集Pfd.
(3) 特征点提取. 采用连通域分析方法对Pfd进行聚类，采用ChESS算子提取Pfd中每个聚类所对应的特征点，实现特征点集Pf的提取.
(4) 初始角点检测. 将Pf中满足临近特征点对称性、 对角特征点对称性和临近特征点夹角范围的特征点置为初始角点.
(5) 角点提取. 以初始角点为起始点，通过估计其它角点位置，在位置误差范围内将Pf相应角点位置处的特征点置为角点.
(6) 角点数据行对齐. 判断已搜索到的角点行中是否含有两个相邻的正常角点行. 若已搜索到两个相邻正常角点行，则采用正常角点行对已搜索到的其它角点行进行数据对齐，使相邻角点行满足对称性要求； 若搜索结束仍未找到两个相邻正常角点行，则将当前棋盘图像作为异常图像处理.
(7) 角点数据列对齐. 对经过行对齐的角点数据进行列对齐. 对齐时，首先在位置误差范围内检测满足对称性要求的连续3列角点数据，然后以该3列数据为基础对角点数据进行列对齐，使每列角点数据满足对称性要求.
(8) 亚像素角点检测. 以检测到的角点为初值对角点位置进行亚像素估计.
在上述过程中，正常角点行是检测其它角点或校正已检测到角点的依据，能否检测到两个相邻的正常角点行是算法能否实现的关键.
4 实验结果与分析为检验本文所提出角点检测方法的有效性，采用http： //www.vision.caltech.edu/bouguetj/calib_doc/提供的25幅棋盘图像进行特征点检测、 角点检测和摄像机标定实验.
4.1 特征点检测实验特征点检测是实现角点检测的基础. 棋盘图像特征点检测的好坏直接影响后续角点检测效果. 检测到的棋盘图像特征点应包含尽量多的角点和尽量少的噪声点. 为检验特征点检测方法的有效性，本实验分别采用Harris算子、 简化的ChESS算子(simple ChESS，SChESS)和ChESS算子作为候选特征点对称性评价方法进行特征点检测. 其中，采用Harris算子时，将Harris算子的角点响应值作为候选特征点的对称性度量值，取一个聚类中具有最高响应值的候选特征点为候选特征点； 若在一个聚类中含有多个具有最高角点响应值的候选特征点，则取这些候选特征点的中心点为特征点. SChESS算子是指在计算对称响应值时，将式(3)简化为下式进行计算：
由于特征点检测可看作棋盘图像角点的预检测，因此可通过统计特征点中所含角点的个数衡量特征点检测方法的性能. 假设检测得到的特征点集Pf中含有fn个特征点，其中角点个数为cn，则角点预检测准确率可表示为
| 特征点检测方法 | 检测的特征点个数 | 角点预检测准确率/% |
| Harris | 3 916 | 39.84 |
| SChESS | 3 939 | 39.60 |
| ChESS | 2 296 | 67.94 |
 |
| 图 7 特征点检测Fig. 7 Detection of feature points |
在上述实验中，在给定的实验参数条件下，3种特征点检测方法均可检测出所有的棋盘角点. 但由实验结果表 1和图 7可见，采用Harris算子和SChESS算子的检测方法在检测到角点的同时也包含大量噪声点，角点预检测准确率较低. 由图 7(b)和7(c)可见，由于大量噪声的存在，在一定程度上破坏了角点间所具有的对称性，使得后续角点检测变得困难. 而采用ChESS算子的检测方法，在检测角点的同时可有效减少噪声点，提高角点预检测准确率，便于根据特征点所具有的对称性进行角点检测.
4.2 角点检测实验为检验本文所提出棋盘图像角点检测方法的有效性，本实验采用特征点检测实验中设置的实验参数，角点位置误差取5个像素，对25幅棋盘图像进行角点检测. 实验中，首先求出棋盘图像候选特征点集Pfd，然后根据Pfd通过聚类和对称性计算提取特征点集Pf，通过分析特征点集Pf的对称性提取初始角点，最后以初始角点为起始点进行角点检测. 由于每幅图像中含有156个角点，因此25幅实验图像共包含3 900个角点.在本文所提出的角点检测方法中，由于角点数据列对齐对保证角点检测的正确性具有重要作用，因此在实验中分别比较了进行列对齐和未进行列对齐对角点检测结果的影响. 实验对比结果如表 2所示. 其中，正确角点个数是指检测到的正确角点的数目，正确图像幅数是指25幅图像中所有角点都正确检测出的图像幅数，无列对齐是指在进行角点检测时未进行列对齐这一步骤的角点检测方法. 典型的棋盘图像角点检测结果如图 8所示. 其中，检测出的角点位置用白色圆点表示.
|
角点检 测方法 | 正确角 点个数 | 错误角 点个数 | 角点检测 正确率 /% | 正确图 像幅数 | 错误图 像幅数 | 图像检测 正确率 /% |
| 无列对齐 | 3 892 | 8 | 99.79 | 23 | 2 | 92.00 |
| 列对齐 | 3 900 | 0 | 100.00 | 25 | 0 | 100.00 |
由实验结果表 2和图 8可见，采用本文所提出的角点检测方法可有效检测出棋盘图像的角点. 其中，由表 2可以看出，虽然未进行列对齐的角点检测方法可以获得很高的角点检测正确率，但由于检测到的错误角点位于两幅图像中，因而造成图像检测正确率降低. 而经过角点数据列对齐后，本文方法能有效提高图像检测的正确率，避免角点误检和错检情况的产生，从而实现棋盘图像角点的自动检测. 以初次检测到的角点为初值，采用亚像素角点检测方法可有效提高角点检测的精度，实现角点的精确检测. 为进一步检验角点检测方法的精度，需通过摄像机标定实验对检测到的角点进行检验.
 |
| 图 8 棋盘图像角点检测结果Fig. 8 Results of chess board corner detection |
检验角点检测精度的方法有2种： 一种是根据检测到的角点求解出摄像机内外参数，然后根据角点位置计算出角点在标定模板中的位置，根据计算出的位置与模板中角点实际位置间的误差检验角点检测精度； 另一种方法是根据摄像机内外参数，将标定模板中的角点在图像中进行重投影，根据图像角点重投影误差检验角点检测精度. 本文采用第2种方法检验棋盘图像角点检测精度. 在该方法中，一般角点重投影误差越小表明角点检测精度越高.
为检验本文所提出角点检测方法的角点检测精度，分别对未经过亚像素角点检测和经过亚像素角点检测得到的25幅棋盘图像角点进行重投影实验，重投影误差如图 9所示. 其中，图 9(a)表示未经过亚像素检测的角点重投影误差，图 9(b)为经过亚像素检测后得到角点重投影误差； 图中重投影误差的x轴和y轴分别表示图像行方向和图像列方向. 根据检测到的角点位置计算得到的摄像机内参数如表 3所示. 其中，标定工具箱计算结果为采用Bouguet开发的摄像机标定工具箱计算得到的摄像机内参数[3]； 本文计算结果(无亚像素检测)是指根据未经过亚像素检测得到的角点位置进行摄像机标定得到的结果； 本文计算结果(亚像素检测)是指根据经过亚像素检测后得到的角点位置计算得到的摄像机参数. 在表 1中，σx和σy分别表示角点在x轴和y轴重投影误差的均方差，fx和fy分别表示摄像机x轴和y轴焦距，u0和v0表示图像中心点坐标，αc表示图像倾斜系数，k1和k2表示摄像机径向畸变系数，p1和p2表示摄像机切向畸变系数.
 |
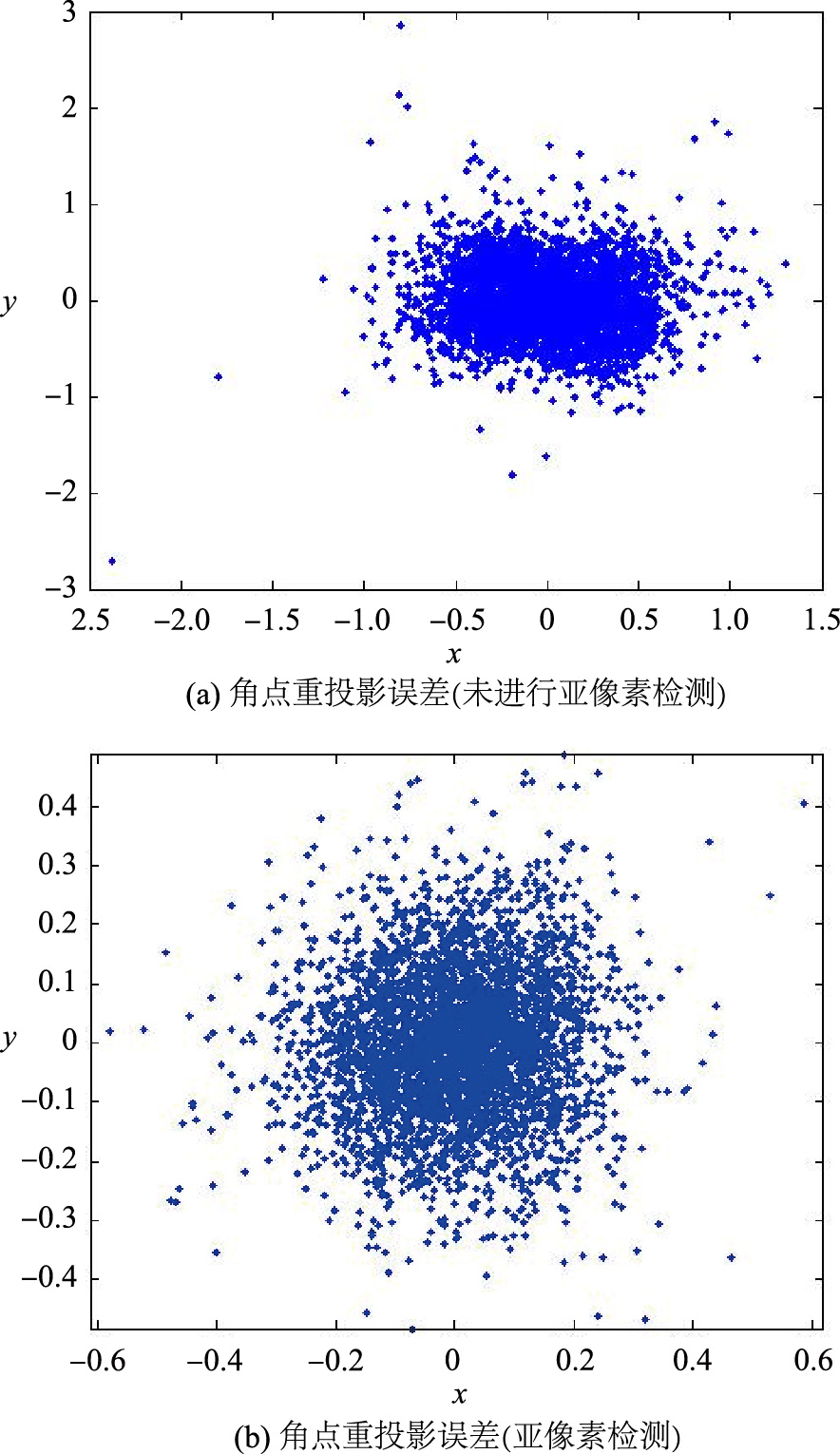| 图 9 角点重投影误差(单位： 像素)Fig. 9 Corner reprojection error (unit： pixel) |
|
摄像机 内参数 | 标定工具箱 计算结果 | 本文计算结果 (无亚像素检测) | 本文计算结果 (亚像素检测) |
| σxσx/pixel | 0.12 | 0.35 | 0.12 |
| σyσy/pixel | 0.12 | 0.38 | 0.12 |
| fxƒx/pixel | 657.30±0.28 | 657.23±0.89 | 657.42±0.30 |
| fyƒy/pixel | 657.74±0.29 | 658.26±0.91 | 657.80±0.31 |
| uoυx/pixel | 302.72±0.59 | 304.65±1.81 | 303.87±0.62 |
| v0υy/pixel | 242.33±0.56 | 244.34±1.73 | 244.39±0.59 |
| αc(×10-3) | 0.42±0.19 | 0.00±0.00 | 0.00±0.00 |
| k1(×10-2) | -25.35±0.23 | -24.50±0.72 | -25.52±0.24 |
| k2(×10-2) | 11.87±0.94 | 9.12±2.94 | 12.59±1.01 |
| p1(×10-3) | -0.28±0.12 | -0.24±0.38 | -0.27±0.13 |
| p2(×10-3) | 0.05±0.12 | 0.11±0.38 | 0.03±0.13 |
由棋盘图像角点重投影误差实验结果图 9(a)可见，未经过亚像素检测得到的棋盘图像角点在x轴和y轴的重投影误差均小于3个像素，重投影误差大多集中在1个像素范围内，重投影误差的均方差在x轴和y轴分别约为0.35和0.38个像素. 由表 3给出的摄像机标定结果可以看出，即便不进行角点亚像素检测，采用本文提出的角点检测方法依然可以得到较好的角点检测精度，摄像机标定结果满足一般应用要求. 由实验结果图 9(b)可以看出，以检测到的角点为初始点，通过亚像素检测，得到的棋盘图像角点在x轴和y轴的重投影误差均小于0.6个像素，角点重投影误差大多集中在0.2个像素范围内，角点重投影误差的均方差约为0.12个像素. 由摄像机标定实验结果表 3可见，采用检测到的角点位置进行摄像机标定得到的摄像机内参数与Bouguet推荐的摄像机参数具有较好的一致性. 但与Bouguet开发的摄像机标定工具箱相比，本文方法无需采用人机交互方式确定棋盘图像角点位置范围，可实现角点自动检测. 综上所述，本文所提出的棋盘图像角点检测方法具有较高的检测精度，适合在摄像机标定中使用.
5 结论本文提出一种新的基于对称性分析的棋盘图像角点自动检测方法. 该方法根据棋盘图像具有对称性的特点，通过对棋盘图像候选特征点集进行聚类，采用ChESS算子计算每个聚类所对应的特征点，实现了棋盘图像特征点集的提取. 为从特征点集中提取角点，采用先检测初始角点然后以初始角点为起始点检测其它角点的方法，实现了棋盘图像的角点检测. 实验结果表明，本文方法检测到的棋盘图像角点具有较好的精度，为解决棋盘图像角点自动检测提供了新的思路，适用于摄像机标定. 同时，本文所提出的方法是一种开放的方法框架，具有较大的研究和改进空间. 下一步工作主要集中在进一步提升角点检测精度，提高算法鲁棒性. 同时进一步研究摄像机畸变程度较高情况下棋盘图像角点的自动检测问题.
| [1] | Hartley R, Zisserma A. Multiple view geometry in computer vision[M]. Cambridge, UK: Cambridge University Press, 2004. |
| [2] | Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. |
| [3] | Bouguet J Y. Camera calibration toolbox for matlab[CP/OL]. (2013-12-02)[2014-03-05]. http: //www.vision.caltech.edu/bouguetj/calib_doc. |
| [4] | 罗钧, 王莲, 侯艳, 等. 摄像机标定的棋盘格亚像素角点检测[J]. 重庆大学学报: 自然科学版, 2008, 31(6): 615-618. Luo J, Wang L, Hou Y, et al. Sub-pixel corner detection of tessellated picture based on camera calibration[J]. Journal of Chongqing University: Natural Science Edition, 2008, 31(6): 615-618. |
| [5] | 杨幸芳, 黄玉美, 高峰, 等. 用于摄像机标定的棋盘图像角点检测新算法[J]. 仪器仪表学报, 2011, 32(5): 1109-1113. Yang X, Huang Y, Gao F, et al. New corner detection algorithm of chessboard image for camera calibration[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 1109-1113. |
| [6] | 吴海滨, 周英蔚, 周雨润, 等. 基于Hessian矩阵的黑白棋盘格角点检测[J]. 大气与环境光学学报, 2013, 8(5): 395-400. Wu H B, Zhou Y W, Zhou Y R, et al. Corner detection of black white checkerboard based on Hessian matrix[J]. Journal of Atmospheric and Environmental Optics, 2013, 8(5): 395-400. |
| [7] | de la Arturo E, Armingol J M. Automatic chessboard detection for intrinsic and extrinsic camera parameter calibration[J]. Sensors, 2010, 10(3): 2027-2044. |
| [8] | Chu J, An G L, Wang L. Chessboard corner detection under image physical coordinate[J]. Optics & Laser Technology, 2013, 48: 599-605. |
| [9] | Hu X, Du P, Zhou Y. Automatic corner detection of chess board for medical endoscopy camera calibration[C]//Proceedings of the 10th International Conference on Virtual Reality Continuum and Its Applications in Industry. 2011: 431-434. |
| [10] | He J, Xia J, Xu X, et al. Automatic corner detection and localization for camera calibration[C]//Proceedings of 10th International Conference on Electronic Measurement & Instruments. 2011: 312-315. |
| [11] | 屠大维, 张翼成. 基于灰度差异的棋盘格角点自动检测[J]. 光学精密工程, 2011, 19(6): 1360-1366. Tu D W, Zhang Y C. Auto-detection of checkerboard corners based on grey-level difference[J]. Optics and Precision Engineering, 2011, 19(6): 1360-1366. |
| [12] | 刘奇琦, 龚晓峰. 一种二值图像连通区域标记的新方法[J]. 计算机工程与应用, 2012, 48(11): 178-180. Liu Q Q, Gong X F. New algorithm for binary connected component labeling[J]. Computer Engineering and Applications, 2012, 48(11): 178-180. |
| [13] | 高红波, 王卫星. 一种二值图像连通区域标记的新算法[J]. 计算机应用, 2007, 27(11): 2776-2777. Gao H B, Wang W X. New connected component labeling algorithm for binary image[J]. Journal of Computer Applications, 2007, 27(11): 2776-2777. |
| [14] | Chu J, Miao J, Zhang G, et al. Edge and corner detection by color invariants[J]. Optics & Laser Technology, 2013, 45(3): 756-762. |
| [15] | Rosten E, Porter R, Drummond T. Faster and better: A machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 105-119. |
| [16] | Mokhtarian F, Mohanna F. Performance evaluation of corner detectors using consistency and accuracy measures[J]. Computer Vision and Image Understanding, 2006, 102(1): 81-94. |
| [17] | Bennett S, Lasenby J. ChESS-Quick and robust detection of chess-board features[J]. Computer Vision and Image Understanding, 2014, 118(1): 197-210. |
| [18] | Zhu Q, Wu B, Wan N. A sub-pixel location method for interest points by means of the Harris interest strength[J]. The Photogrammetric Record, 2007, 22(120): 321-335. |