1 引言
在群体协同[1]问题中，个体成员的合理选择与有效分组对合作的质量和效率起着至关重要的作用，可以充分发挥协同成员的主观积极性和个人能力，同时，密切的协同配合也是高效率完成工作的保证. 然而，由于选择协同成员需要考虑的影响因素繁多，而且层次不一，因此，无法通过简单的直观判断做出合理的人员配置方案.
近年来，很多研究者对主观偏好和群体协同成员的选择以及评价方法进行了模型化和定量化的研究. 如Xu[2]和Gong[3]利用刚性量化指标、 采用主观赋权法得到决策者偏好的权重信息，建立合作伙伴选择决策模型；
Cheng[4]提出在群决策中考虑决策者对决策重要性认识的偏好来确定属性权重的方法； Liu[5]研究了知识交互对群体决策观点演化的影响，并提出演化模型. 目前，大多数相关研究是基于量化的权重信息[6]来确定个性偏好和决策，很少强调个体成员个性偏好的匹配及其对于群体协同的影响. 实际上，群体协同人员的个性偏好在群体协同过程中往往是变化的，协同成员在彼此沟通和反馈之后，观点也可能会相应改变[7]. 因此，有必要通过对个体偏好的语义信息及逻辑推理进行深入的探讨.
面向处理在群体协同过程中个体偏好的优化配置问题，本文建立了协同人员的主观偏好的心理学模型，进而对群体协同人员的个性偏好特征模型进行分析，利用逻辑关系推理群体协同成员对管理者的偏好语义逻辑编码信息，在此基础上对群体协同人员配置方案进行满意度排序，以确定优化的协同人员优化配置.
2 个性偏好模型 2.1 群体协同人员选择与评价特征协同一词在英文中有synergy、 collaboration、 cooperation、 coordination等多种表述，在汉语中是齐心协力、 互相配合的意思. 1971年，德国学者Haken在系统论中最早提出协同的概念，指系统中各子系统的相互协调、 合作或同步的联合作用及集体行为，结果是产生1+1>2的协同效应[8]. 它是促进团体正常并且有效运作的基础.
在进行协同人员选择时，一般依据的是知识结构、 协作素质、 工作经验、 学习兴趣和技能水平等作为特征信息，并将性格、 学习风格以及偏好等构成协同人员的个性偏好特征，形成群体协同人员选择与评价特征，如图 1所示[9].
 |
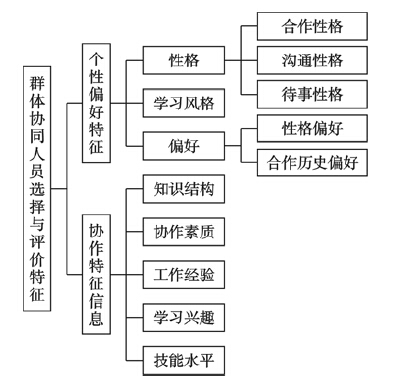| 图 1 群体协同人员选择与评价特征Fig. 1 Group collaborative personnel selections and evaluation characteristics |
进行群体协同中管理者与协同成员的优化配置，实现协同管理效益最大化，需要了解和掌握管理者和协同成员的个性特性，即个性偏好，它由先验偏好和调节偏好共同构成[10]：
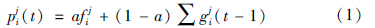
假设第k次合作对偏好的影响权重为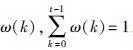
，偏好值为αji(k). αji(k)采用模糊语言集合｛极好，很好，好，较好，一般，较差，差，很差，极差｝描述，并转化为离散数值区间｛0.9，0.8，0.7，0.6，0.5，0.4，0.3，0.2，0.1｝. 同时，设管理者i的记忆衰减函数为y
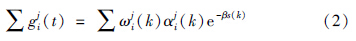
通常，管理者对协同成员的不同个性有喜爱的偏好，这种个性偏好称为先验偏好或最初偏好，用离散程度计算式表示，一般可认为是常数值：
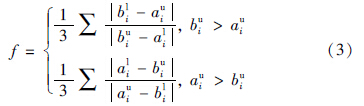
一般通过相关数据，可采集和提取管理者和协作成员的性格特征，根据性格语言效用值对应值(如表 1所示[12])进行相应数值转换，设管理者性格语言效用值区间数为[bli，bui](i=1，2，3)，其中bli和bui分别表示下限和上限. [ali，aui]为协同成员性格语言效用值区间数.
| 区间数值 | (0，0.2) | (0.1，0.3) | (0.2，0.4) | (0.4，0.6) | (0.5，0.7) | (0.7，0.9) | (0.8，1) | |
|
语言 效用值 | 合作性格 | 领导型 | 服从型 | 合作 | ||||
| 沟通性格 | 很内向 | 内向 | 较内向 | 一般 | 较外向 | 外向 | 很外向 | |
| 待事性格 | 很悲观 | 悲观 | 较悲观 | 一般 | 较乐观 | 乐观 | 很乐观 |
综合式(1)和式(2)可得到主观偏好模型表达式：
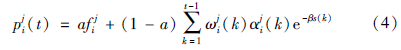
群体协同成员的协作特征信息评价可以在考虑个性偏好的基础上进行计算，以此对每个协同成员进行选择排序，找出最满意的协同伙伴[13].
用模糊语言集合｛极大，很大，大，较大，一般，较小，小，很小，极小｝表示学习兴趣度，这里设定管理者的兴趣领域子类有M个，利用向量空间模型表示管理者i的兴趣向量Qi=(qi1，qi2，…，qim)，利用模糊聚类的思想，可以计算管理者i与不同协同成员j的兴趣向量的相似关系R[14]，可表示为
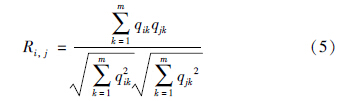
其它协作特征信息评价方式的计算方法与此类似.
3 偏好语义逻辑编码在通过个性偏好模型确定符合实际需求的群体协同人员配置方案后，若方案存在人员分配冲突，则需要用多元变量组合的形式表示所有可能的人员配置组合[15]，将用于后续的逻辑推理.
定义AiBi…Ni(i=1，2，…)，其中A，B，…，N表示不同协同人员，i表示各个管理者，这样就可以用多元变量组合表示某一种人员配置组合情况.
所谓偏好语义逻辑编码就是将形式条件语句用优先目标集来表示，每一个目标集表示一种可能性情况，并且在转化成优先目标集后都有一个权重值作为标尺，最后将用于集合成全局满意度水平. 此处的偏好语义表述特指协同成员在复合条件下对管理者的主观偏好表述. 例如，偏好表述的形式条件语句为“在c中，a优先于b”，这时偏好可建模为一对优先目标集｛(¬c∨a∨b，1)(¬c∨a，1-α)｝，具体含义为“当c为真时，必须有a或b(只能在a和b中选择)，并且在c中，必要条件是有a为真. ”这些成对的关联水平未知的命题公式被称为可能性公式[16]. (¬c∨a，1-α)表示当约束被违反的满意度的上限是α. 当条件偏好语句被转化成逻辑编码符号时，由于不能准确地知道偏好的必要性程度，权重就成为有效的处理方式. 通常权重被设定为一个线性序列标度(“>”是决策空间上的二元关系，严格的偏序关系用“>”表示)，具有上限值(表示为1)和下限值(表示为0). 每一个条件偏好转化成优先目标集后都有一个权重值作为标尺，最后集合成全局满意度水平，根据全局满意度水平值的大小可以制定出条件偏好网络的矢量偏序图.
注意当b≡¬a，语句(¬c∨a∨b，1)为同义反复，就不需要表示出来了，事实上，语句(¬c∨a，1-α)是表达偏好在c中a包含¬a，当a∨b不能包含所有可能的选择语句时，(¬c∨a∨b，1)是必须的. 假设a∨b≡¬d(当¬d不是同义反复)，这样就使得在c中，偏好a包含偏好b有意义. 事实上,在c中，如果a无效，则b是一个错误的选择. 如果想表示余下的选择的话，可以用(¬c∨a∨b，1-α′)代替(¬c∨a∨b，1)，其中1-α′>1-α，这样，该方法很容易扩展到非二元的选择问题[17].
4 人员选择与优化配置在当前国内外的研究中，研究者对异质分组方式都有赞同的态度，在调查实验中己得到证实. 但是，同质分组[18]也在一些协同任务中能起到很好的作用，它有正面且积极的影响效果. 本文探讨的方法是在同质分组的基础上，考虑当管理者与其品性相投的协同伙伴进行合作时，更容易激发出每个人的积极性和创造性.
首先，通过管理者和协同成员的个性偏好模型分析，确定理想协同伙伴的目标特征； 在此基础上，按照特征相似的原则，通过模糊聚类[19]筛选找出特征匹配的协同成员候选人. 由于多个群体的管理者在选择最佳协同成员时，某一个协同成员可能成为多个管理者的意向成员. 对于选择冲突的问题，如果管理者和协同成员是一对一的单选问题，即可按照博弈论方法，求取一个纳什均衡点，计算满意度的变化率，以此来选择协同成员的最优方案[20]. 这里，可以将可组合方案用多元变量表示，同时，对协同成员偏好语义表述信息进行逻辑编码，用逻辑符号信息来表达协同成员的主观偏好，通过逻辑推理得出全局满意度矢量偏序图，找出达到整体最优的群体协同人员优化配置方案.
人员选择与配置优化算法流程如图 2所示.
 |
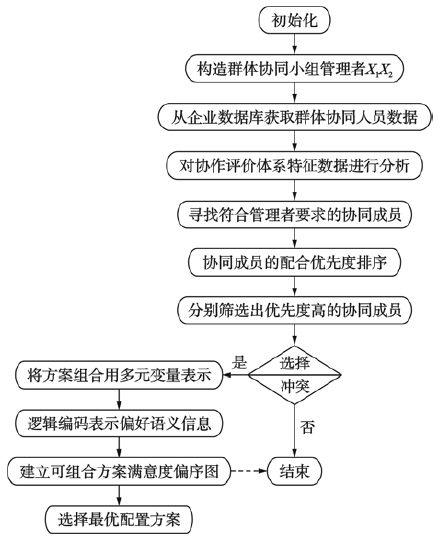| 图 2 人员选择与配置优化算法Fig. 2 Personnel selection and allocation optimum algorithms |
算法的具体实现步骤如下：
Step 1：构造特征矩阵Xnm，进行模糊聚类
依照协作特征信息指标构造群体管理者与协同成员的特征矩阵，可以从相关的人员数据信息中进行采集和提取.
(1) 对特征矩阵Xnm进行标准化处理
平移*标准差变换：
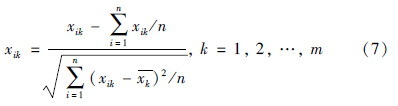
平移*极差变换：
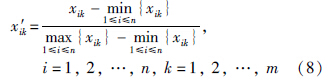
(2) 建立模糊相似矩阵
利用相关系数法构造模糊相似矩阵R=(rij)nm，rij表示xi和xj的相似程度：
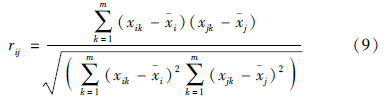
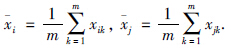
(3) 建立模糊等价关系矩阵
根据模糊相似矩阵R，用平方法求R的传递闭包t(R)=R*. 求R2=R·R，R4=R2·R2，…. 经n次褶积运算后，得到R2n=R2n+1. R*=R2n即是所求模糊等价矩阵.
(4) 模糊聚类
根据模糊等价矩阵R*，选取不同的置信水平λ，可以得到不同的归类情况. 一般来说，随着λ值由1到0不断减小，聚类结果由细到粗，可以得到动态的聚类图. 调整λ可以得到最接近实际情况的分类方案.
Step 2：协同成员的偏好排序
对确定的符合实际需求的分类结果中的群体协同成员进行个性偏好值排序，偏好值最大的Pij就是对应xji的最佳协同伙伴，通过这个排序，按照协同成员的数目可以选择最佳的协同小组成员. 若不存在选择冲突则结束算法，否则进行Step 3.
Step 3：偏好语义逻辑编码和逻辑推理
(1) 针对群体协同人员配置中存在的选择冲突情况，在满足条件情况下，依据配合优先度排序，可以对可能方案组建协同小组，并用多元变量组合进行表示.
(2) 对协同者的偏好语义信息进行逻辑编码，将形式条件语句用优先目标集来表示，最后通过逻辑推理集合成全局满意度水平，构建矢量偏序图，找出最优的配置方案.
5 实例研究对于群体协同人员优化配置问题，考虑企业对一批员工进行分组培养，每个管理者分别要选择自己的组员，为实现协同管理效益最大化，需要了解和掌握管理者和协同成员的个性特性，通过相关的企业信息系统数据，可以采集和提取管理者和协同成员的特征数据并进行分析.
考虑2位管理者和8位协同成员，管理者需要建立各自的群体协同团队，每个团队包括3个成员. 分别用x1，x2，…，x10来表示个体成员，其中x1，x2表示管理者，x3，…，x10表示协同成员. 每个个体成员用特征评价指标体系中协作特征信息的5个指标来描述，建立个性特征模型，如表 2所示.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | |
| 知识结构 | 9 | 9 | 9 | 5 | 6 | 6 | 8 | 8 | 8 | 6 |
| 协作素质 | 9 | 6 | 7 | 6 | 8 | 4 | 6 | 9 | 5 | 9 |
| 工作经验 | 8 | 7 | 6 | 5 | 8 | 5 | 6 | 6 | 7 | 8 |
| 学习兴趣 | 7 | 6 | 8 | 7 | 6 | 8 | 7 | 7 | 8 | 7 |
| 技能水平 | 8 | 8 | 5 | 9 | 9 | 7 | 9 | 9 | 9 | 8 |
Step 1：获得初始化矩阵如下：
生成的模糊相似矩阵为
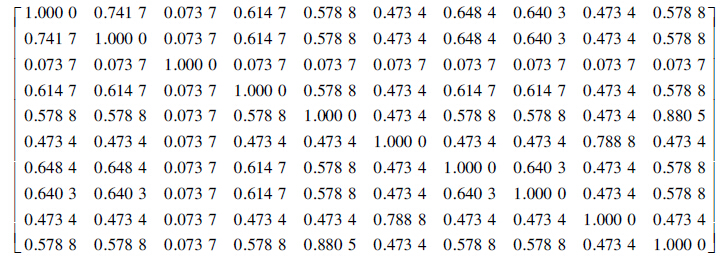
对于管理者选择各自协同小组成员的模糊相似矩阵进行模糊聚类，调节λ的取值，理想情况下的聚类分组是使x1和x2归为不同的组别中，且刚好每组的人数至少满足3个人，这样协同小组的分组就圆满结束，但实际情况往往是处于非理想情况. 当λ为0.57时产生3个聚类，即｛x1，x4，x5，x7，x8，x10｝、 ｛x2，x4，x5，x7，x8，x10｝和｛x1，x2，x4，x5，x7，x8，x10｝.
Step 2：聚类后筛选出的协同成员的性格和合作历史特征见表 3、 表 4.| 协同成员 | 合作性格 | 沟通性格 | 待事性格 |
| x4 | 合作型(0.7 0.9) | 内向(0.1 0.3) | 悲观(0.1 0.3) |
| x5 | 领导型(0.1 0.3) | 中等(0.4 0.6) | 中等(0.4 0.6) |
| x7 | 领导型(0.1 0.3) | 外向(0.7 0.9) | 乐观(0.7 0.9) |
| x8 | 服从型(0.4 0.6) | 中等(0.4 0.6) | 乐观(0.7 0.9) |
| x10 | 服从型(0.4 0.6) | 内向(0.1 0.3) | 中等(0.4 0.6) |
|
协同 成员 | 合作 次数 | 合作结果 | 合作时间 / 年 | 影响 程度 | 权重 系数 |
| x4 | 1 | 很差(0.2) | 0.20 | 3 | 0.43 |
| 2 | 很好(0.8) | 0.15 | 3 | 0.43 | |
| 3 | 一般(0.5) | 0.10 | 1 | 0.14 | |
| x5 | 1 | 较好(0.6) | 0.10 | 1 | 1 |
| x7 | 1 | 好(0.5) | 0.30 | 1 | 0.14 |
| 2 | 差(0.3) | 0.20 | 2 | 0.28 | |
| 3 | 好(0.7) | 0.10 | 1 | 0.14 | |
| 4 | 很好(0.8) | 0.05 | 3 | 0.42 | |
| x8 | 1 | 差(0.3) | 0.20 | 2 | 0.43 |
| 2 | 好(0.5) | 0.10 | 3 | 0.57 | |
| x10 | 1 | 好(0.5) | 0.15 | 3 | 0.48 |
| 2 | 差(0.3) | 0.10 | 1 | 0.33 | |
| 3 | 很好(0.8) | 0.03 | 2 | 0.35 |
选择前两个聚类分组，计算协同成员对于不同管理者偏好下的主观偏好值. 利用式(1)，由表 1和表 3可以计算出针对管理者x1的分组集合中协同成员的先验偏好值：
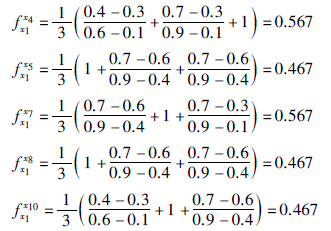
利用式(3)，由表 4可以计算出调节偏好值：
先验偏好权重系数设定为0.6，代入式(4)即可得出管理者对协同成员的主观偏好值：
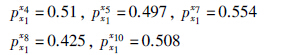
对于管理者x1的协同成员配合优先度排序结果是：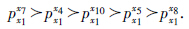
按照同样的方法，可以计算出针对管理者x2的聚类分组中各个协同成员的协同配合优先度排序是：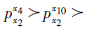
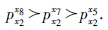
由于每个管理者需要选取2个协同成员，此时会存在选择冲突.
Step 3：在满足条件的情况下，依据配合优先度排序，可以对聚类分组方案x1，x4，x7，x10和x2，x4，x8，x10组建两个项目协同小组，并对其协同成员的归属进行二元变量表示，即(A1，B1，E1，A2，C2，D2)，其中A1表示x4在x1的协同组中，B1表示x7在x1的协同组中，以此类推.
这样，可制定出所有可能的人员配置组合情况集合为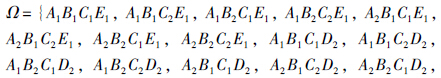
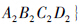，要对16种情况进行优化排序筛选，还要获得每个协同成员对于管理者的偏好语义表述，并将其进行逻辑符号编码，问题就转化为对16种情况的排序筛选问题.
获得协同成员偏好语义表述语句如下：
A，即协同成员x4表述为： 偏向于选择管理者x1；
B，即协同成员x7表述为： 偏向于选择管理者x1；
C，即协同成员x8表述为： 若A和B同时偏向管理者x1，我偏向于管理者x1，否则偏向管理者x2；
D，即协同成员x10表述为： 若C偏向于管理者x1，我退出，否则偏向管理者x2.
则，A可编码为(i)： ｛A1，1-α｝；
B可编码为(ii)： ｛B1，1-β｝；
C可编码为(iii)： ｛(¬A1∨¬B1∨C1，1-γ)｝，
(iv)： ｛(¬A2∨¬B2∨C1，1-η)｝，
(v)： ｛(¬A2∨¬B1∨C2，1-δ)｝，
(vi)： ｛(¬A1∨¬B2∨C2，1-ε)｝；
D可编码为(vii)： ｛(¬C1∨E1，1-θ)｝，
(viii)： ｛(¬C2∨D2，1-ρ)｝.
由于权重值1-α，1-β，1-γ，1-η，1-δ，1-ε，1-θ，1-ρ未知，所以它们没有特定的序列排序，但是16种选择方案之间的概率排序可以自然地诱导. 表 5给出了上述16种人员配置方案的满意度水平. 最后一列给出了全局满意度水平，对应地表示出人员配置组合在编码后的权重值信息. 这里，计算权重值信息的方法是参照了文[21]中所提出的语法方法.
| (i) | (ii) | (iii) | (iv) | (v) | (vi) | (vii) | (viii) | 满意度水平 | |
| A1B1C1E1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | (1，1，1，1，1，1，1，1) |
| A1B1C2E1 | 1 | 1 | γ | 1 | 1 | 1 | 1 | ρ | (1，1，γ，1，1，1，1，ρ) |
| A1B2C1E1 | 1 | β | 1 | 1 | 1 | ε | 1 | 1 | (1，β，1，1，1，ε，1，1) |
| A1B2C2E1 | 1 | β | 1 | 1 | 1 | 1 | 1 | ρ | (1，β，1，1，1，1，1，ρ) |
| A2B1C1E1 | α | 1 | 1 | 1 | δ | 1 | 1 | 1 | (α，1，1，1，δ，1，1，1) |
| A2B1C2E1 | α | 1 | 1 | 1 | 1 | 1 | 1 | ρ | (α，1，1，1，1，1，1，ρ) |
| A2B2C1E1 | α | β | 1 | 1 | 1 | 1 | 1 | 1 | (α，β，1，1，1，1，1，1) |
| A2B2C2E1 | α | β | 1 | η | 1 | 1 | 1 | ρ | (α，β，1，η，1，1，1，ρ) |
| A1B1C1D2 | 1 | 1 | 1 | 1 | 1 | 1 | θ | 1 | (1，1，1，1，1，1，θ，1) |
| A1B1C2D2 | 1 | 1 | γ | 1 | 1 | 1 | 1 | 1 | (1，1，γ，1，1，1，1，1) |
| A1B2C1D2 | 1 | β | 1 | 1 | 1 | ε | θ | 1 | (1，β，1，1，1，ε，θ，1) |
| A1B2C2D2 | 1 | β | 1 | 1 | 1 | 1 | 1 | 1 | (1，β，1，1，1，1，1，1) |
| A2B1C1D2 | α | 1 | 1 | 1 | δ | 1 | θ | 1 | (α，1，1，1，δ，1，θ，1) |
| A2B1C2D2 | α | 1 | 1 | 1 | 1 | 1 | 1 | 1 | (α，1，1，1，1，1，1，1) |
| A2B2C1D2 | α | β | 1 | 1 | 1 | 1 | θ | 1 | (α，β，1，1，1，1，θ，1) |
| A2B2C2D2 | α | β | 1 | η | 1 | 1 | 1 | 1 | (α，β，1，η，1，1，1，1) |
由表 5可以看出，A1B1C1E1的满意度水平优于其它所有的选择方案，主要是它最满足协同成员的基本偏好语义表述要求，但是却不符合两个小组人员的均衡分配要求. 同样，A2B1C2D2优先于A2B2C1E1是因为A2B1C2D2被违反的上限界是(A1，1-α)，而A2B2C1E1被违反的上限界是(A1，1-α)和(B1，1-β). 由此依据可以制定出矢量偏序图，如图 3所示，有向箭头由A2B1C2D2指向A1B1C1E1表示A1B1C1E1更优先于A2B1C2D2.
 |
| 图 3 矢量偏序图Fig. 3 Vector partial order diagram |
最后，结合实际情况来看，满足两个项目组人员优化配置基本要求的分组方案集合为｛A1B2C2E1，A2B1C2E1，A2B2C1E1，A1B1C2D2，A1B2C1D2，A2B1C1D2｝(即图 3中加双下划线的配置方案)，由有向序列偏序图可以看出A1B1C2D2是最优、 最合理的人员配置方案，即由x1，x4，x7和x2，x8，x10 组建的两个项目协同分组方案符合企业整体效益配置最优的要求.
6 结论针对群体协同人员选择和优化配置问题，以个性偏好模型为基础，提出了一种基于个体偏好语义表述的群体协同人员配置方法. 结合协同人员主要特征评价指标体系以及模糊聚类算法计算主观偏好，并进行优先度排序，在解决群体协同人员配置冲突问题时，提出了运用逻辑符号表示协同成员语义偏好表述信息的方法，通过逻辑推理制定全局满意度矢量偏序图，更直观地表示项目组管理者与协同成员主客体的最优配置方案，同时，能够弥补单纯靠量化的信息数据来建立个性偏好模型过程中产生的与协同人员实际偏好不符合的情况，有效地避免群体协同人员优化配置中隐藏的人员矛盾，对解决多个协同组的人员优化配置问题有更广泛的适用性. 通过实例给出了详细的实现过程，验证了方法的有效性.
本文提出的群体协同人员优化配置方法是在同质分组条件的基础上进行的，对于异质分组的情况还有待进一步的充实和完善.
| [1] | Pei Z, Zou L, Yi L Z. A linguistic aggregation operator including weights for linguistic values and experts in group decision making[J]. International Journal of Uncertainty Fuzziness and Knowledge-based Systems, 2013, 21(6): 927-943. |
| [2] | Xu Z S, Cai X Q. Nonlinear optimization models for multiple attribute group decision making with intuitionistic fuzzy information[J]. International Journal of Intelligent Systems, 2010, 25(6): 489-513. |
| [3] | Gong Y B. Fuzzy multi-attribute group decision making method based on interval type-2 fuzzy sets and applications to global supplier selection[J]. International Journal of Fuzzy Systems, 2013, 15(4): 392-400. |
| [4] | 程平, 刘伟. 多属性群决策中一种基于主观偏好确定属性权重的方法[J]. 控制与决策, 2010, 11(5): 1645-1650. Cheng P, Liu W. Method of determining attributes weights based on subjective preference in multi-attribute group decision-making[J]. Control and Decision, 2010, 11(5): 1645-1650. |
| [5] | 刘军. 基于知识交互视角的群体决策观点动态演化模型[J]. 统计与决策, 2014, 18(5): 53-56. Liu J. Group decision model of the dynamic evolution based on the knowledge interaction perspective view[J]. Statistics & Decision, 2014, 18(5): 53-56. |
| [6] | Chen H Y, Zhou L G. An approach to group decision making with interval fuzzy preference relations based on induced generalized continuous ordered weighted averaging operator[J]. Expert Systems with Applications, 2011, 38(7): 13432-13440. |
| [7] | Gong Z W, Jeffrey F, Zhao Y. The optimal group consensus deviation measure for multiplicative preference relations[J]. Expert Systems with Applications, 2012, 39(8): 11548-11555. |
| [8] | Yehuda K. Collaborative filtering with temporal dynamics[J]. Communications of the ACM, 2010, 12(4): 356-367. |
| [9] | 刘景宜, 杨威. 面向CSCL的主观偏好协作算法研究[J]. 计算机应用与软件, 2010, 27(6): 219-222. Liu J Y, Yang W. On CSCL-oriented algorithm of collaborative partners selection based on subjective preference[J]. Computer Application and Software, 2010, 27(6): 219-222. |
| [10] | 宋李俊, 杨育, 张晓冬. 基于主观偏好的协同设计伙伴评价选择算法研究[J]. 计算机集成制造系统, 2007, 10(2): 2055. Song L J, Yang Y, Zhang X D. Preference-based algorithm for collaborative design partners evaluation & selection[J]. Computer Integrated Manufacturing Systems, 2007, 10(2): 2055-2056. |
| [11] | Zhou L G, Tao Z F, Chen H Y. Some icowa operators and their applications to group decision making with interval fuzzy preference relations[J]. International Journal of Uncertainty Fuzziness and Knowledge-based Systems, 2013, 21(4): 579-601. |
| [12] | Xu Z S. Group decision making model and approach based on interval preference orderings[J]. International Computers & Industrial Engineering, 2013, 64(3): 797-803. |
| [13] | Francesco G, Luigi M, Matteo P. Group membership, team preferences, and expectations[J]. Economic Behavior & Organization, 2013, 86(2): 183-190. |
| [14] | Zhang Y, Ma H X, Liu B H. Group decision making with 2-tuple intuitionistic fuzzy linguistic preference relations[J]. Soft Computing, 2012, 16(8): 1439-1446. |
| [15] | Dong Y C, Zhang G Q, Hong W C. Linguistic computational model based on 2-tuples and intervals[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(6): 1006-1018. |
| [16] | Ferretti E, Errecalde M L, Garcia A J. A possibilistic defeasible logic programming approach to argumentation-based decision-making[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2014, 26(4): 519-550. |
| [17] | Jing L P, Michael K, Joshua Z. Knowledge-based vector space model for text clustering[J]. Knowledge and Information Systems, 2010, 32(6): 245-256. |
| [18] | Rodriguez, Francisco J, Lozano M. An artificial bee colony algorithm for the maximally diverse grouping problem[J]. Information Sciences, 2013, 230(8): 183-196. |
| [19] | Beg I, Rashid T. An improved clustering algorithm using fuzzy relation for the performance evaluation of humanistic systems[J]. International Journal of Intelligent Systems, 2014, 29(12): 1181-1199. |
| [20] | Cabrerizo F J, Perez I J, Herrera-Viedma E. Managing the consensus in group decision making in an unbalanced fuzzy linguistic context with incomplete information[J]. Knowledge-based Systems, 2010, 23(2): 169-181. |
| [21] | Teheux B. Propositional dynamic logic for searching games with errors[J]. Journal of Applied Logic, 2014, 12(4): 377-394. |