2. 山东大学控制科学与工程学院, 山东 济南 250061
2. School of Control Science and Engineering, Shandong University, Jinan 250061, China
1 引言
导弹是现代化武器库中重要的武器，现代战争中使用空地武器对地下目标、 地面机动目标和水面目标进行打击时，为了达到理想的毁伤效果，提高武器在目标区域的生存能力，要求武器在俯冲攻击时，接近垂直下降. 这样一方面可以缩短攻击时间，提高空地制导武器末端的飞行速度，使敌方防空武器来不及准备或准备不充分； 另一方面，可以攻击敌方相对薄弱的顶部，提高空地武器的毁伤效果[1, 2, 3, 4, 5, 6].
制导律的设计是制导武器实现精确制导的关键技术[7, 8]. 要使战斗部能够充分发挥最大效能，取得最佳毁伤效果，落角控制已成为各种空地制导武器研究的热点问题. 目前，国内外许多学者、 科学家和工程师对落角控制方法进行了大量研究，取得了丰硕的成果[9, 10, 11]. 文[12]在二维平面内设计了一种自适应比例制导律，通过改变比例系数来满足末端落角约束，以实现目标的有效拦截. 文[13]设计了一种最优垂直俯冲制导律，其落角接近垂直，落角误差小，但需要估计剩余时间，增加了系统的复杂度. 文[14, 15]推导了一种带有末端落角约束的滑模变结构制导律，其命中精度高，制导效果较好，但没有考虑引入开关函数后对系统产生的抖振. 文[16]利用反演控制法设计了一种带有角度和时间约束的偏置比例导引律，实现了多约束条件下的精确打击，但并没给出相应制导参数的选取范围. 文[17]设计了一种带有偏置项的比例导引律，其末端落角控制效果较好，但在攻击机动目标时落角偏差较大.
目前，对空地制导武器制导律的研究主要集中在比例导引和变结构制导律等方面. 其中，基于比例导引的制导律，由于其拦截非机动目标时弹道性能好、 脱靶量小且易于工程实现，已被普遍采用. 基于此，本文针对空地制导武器对目标打击的特殊末端姿态问题，根据滑模变结构理论对不确定因素干扰有较强鲁棒性的特点，设计了一种具有末端落角约束的滑模变结构制导律，分析了各制导参数对制导性能的影响，并进行了仿真和对比分析.
2 弹—目几何关系为了简化弹—目运动方程，将末制导过程的弹—目相对运动解耦成俯仰平面和偏航平面两个分量的运动. 其中，俯仰平面上的弹—目相对运动分量如图 1所示.
 |
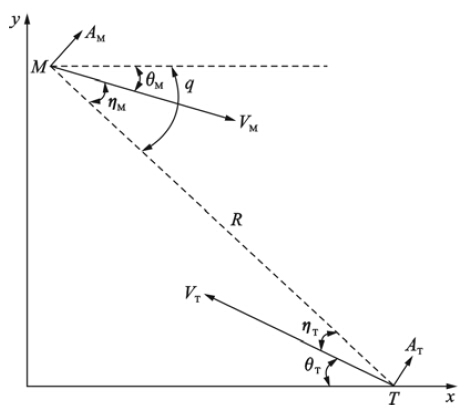| 图 1 二维弹—目相对运动关系Fig. 1 The relative motions of the missile-target in two-dimension |
根据图 1建立弹—目相对运动关系为
以二维弹—目相对运动为数学模型，将导弹末端姿态考虑到滑动模态的设计中，可推导带有末端落角约束的滑模变结构制导律.
末端落角是在空地导弹打击目标过程中，导弹与目标的速度矢量间的夹角[18]，即：
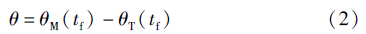
当导弹命中目标时，有=0，由式(1)可得
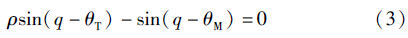
由式(3)可知，当θT和θM给定时，存在唯一的q. 因此，可将末端落角约束问题转化成末端视线角问题：
式(4)中第1个方程表示导弹在末制导时刻可以命中目标，第2个方程表示在末制导时刻满足期望角度命中目标.
选取状态变量：
当式(5)中的两个方程都趋近于0时，导弹不仅可以命中目标，而且还满足落角约束的要求.
对式(5)求导数，得系统状态方程：
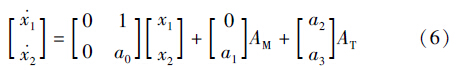
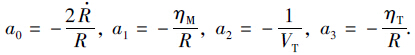由于目标加速度不可直接测得，AT视为干扰量. 因为x1和x2状态变量相关，故设计具有末端落角约束的滑模变结构制导律要求在有限时间内将x1和x2稳定到零点.
导弹在飞行过程中，制导系统不可避免地会受到外界和自身参数变化的影响，因此所设计制导律必须具有较好的鲁棒性[19]. 考虑到滑模变结构控制系统具有良好的抗干扰和抗参数摄动性，因此本文采用滑模变结构控制方法来设计制导律.
为满足导弹命中目标瞬间脱靶量和末端落角要求，设计滑模变结构切换函数为
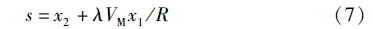
系统状态方程的自适应滑模趋近律可设计为
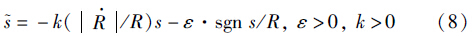
式(8)形式的趋近律的物理意义为： 当弹—目相对距离较大时，适当放慢趋近滑模的速率； 当弹—目相对距离趋近于0时，使趋近律迅速增加，确保不发散，从而使导弹具有较高的命中精度. 对趋近速律进行自适应调节可以有效地削弱绕滑模的抖动.
式(7)两边对时间求导，可得
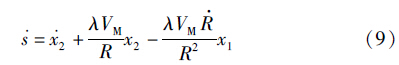
结合式(1)、 (8)和式(9)，可得到滑模变结构制导律为
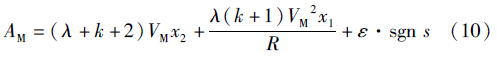
式(10)中含有符号项函数，实际上符号项函数的切换不能瞬间完成，会存在一定的时间滞后，进而使系统产生抖振. 当抖振幅度较大时，就会削弱控制效果[20]. 为了有效减小系统抖振，本文利用高增益连续函数Φ(s)函数代替符号函数项sgn s. Φ(s)可定义为
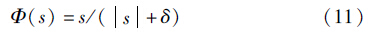
将式(11)代入式(10)，可得
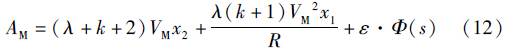
所设计的滑模变结构制导律式(12)中，含有4个制导参数，下文将在仿真中详细讨论各制导参数对制导性能的影响.
4 仿真所设计的滑模变结构制导律包含角度误差项系数λ、 开关项系数ε、 趋近律系数k和常值量δ 4个制导参数. 为了达到较好的制导效果，下面将在详细分析各参数对制导律影响的基础上，通过仿真逐一确定4个制导参数，最后对所设计的制导律进行仿真和对比分析.
4.1 制导参数影响分析由于末端过载过大会导致较大的脱靶量，为保证末端过载收敛，取：
当存在某一个时间t1，且当t∈(t1，tf)时，满足s(t)=0，则式(7)可转化为
将式(13)代入式(14)，可得
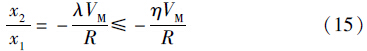
将式(15)两边同时求积分，可得
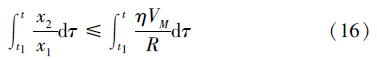
求解不等式(16)，可得
因为在有限时间内，导弹会命中目标，那么式(17)右端趋近于0，即：
将式(18)代入式(14)，可得
当t∈(t1，tf)时，s(t)=0. 将式(19)代入式(10)，得
式(20)表明，当角度误差项系数选取满足式(13)时，系统稳定.
为避免弹—目相对距离过快趋近于0，而系统状态未到达滑模面，取：
构造李亚普诺夫函数如下：
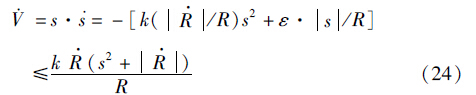
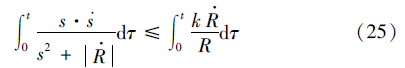
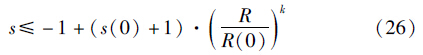
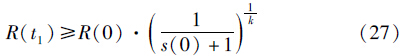
确定4个制导参数较为复杂，应综合考虑制导精度、 落角偏差和法向加速度等因素，在保证精确命中目标的前提下，减小落角偏差，提高打击效果. 本文通过选取多组参数数据进行仿真对比，先获得各参数的取值范围，在此基础上，选取各参数的具体取值.
(1) 角度误差项系数λ
由式(8)可知，角度误差项系数λ的选取决定了切换函数s中落角误差项的权重，虽然λ的取值和趋近律无直接关系，但会影响制导指令和切换函数，其取值范围见表 1.
| 角度误差项系数λ | 开关项系数ε和趋近律系数k | 常值量δ |
| λ≥1 | ε，k>0 | δ>0 |
为便于分析，令k=1.0，ε=1，δ=0.01，观察λ取不同值对系统的影响，仿真结果如图 2所示.
 |
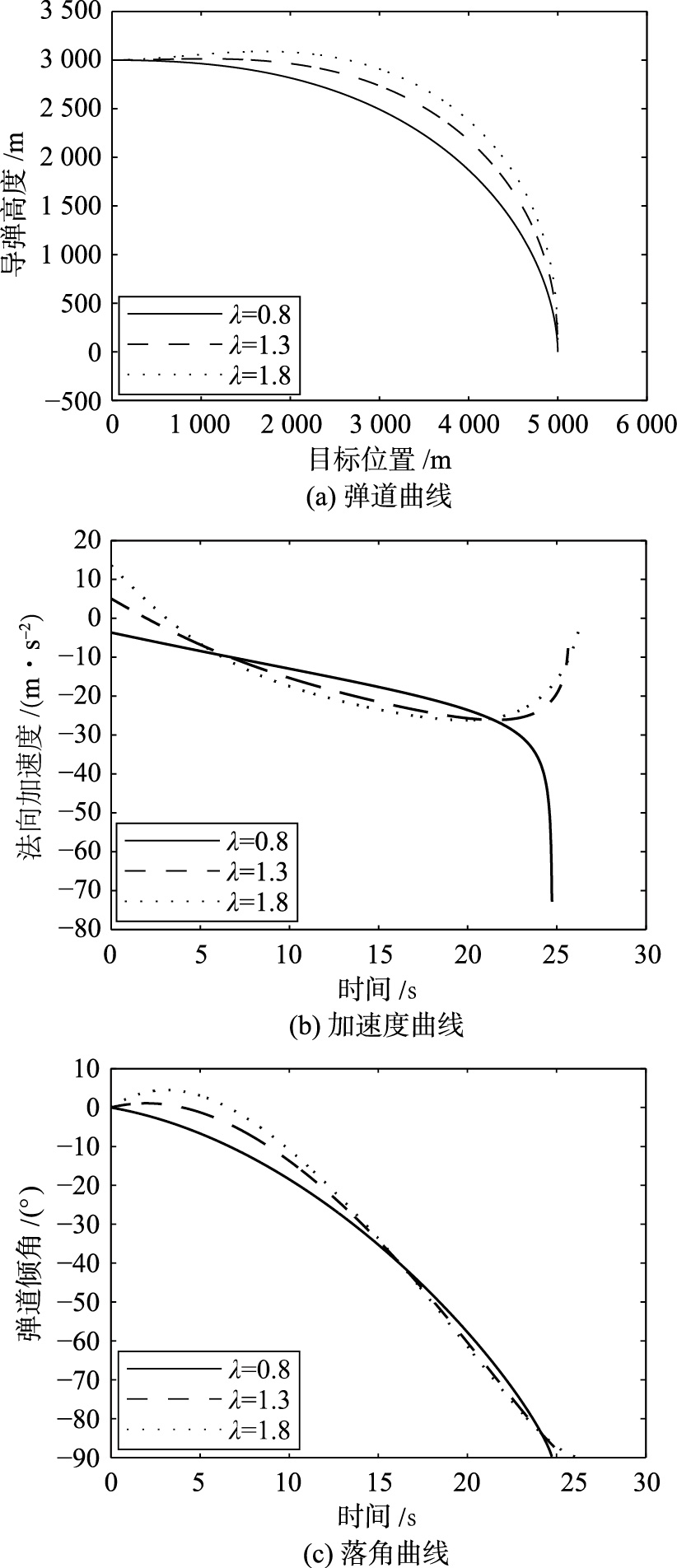| 图 2 λ不同取值下的仿真曲线Fig. 2 The simulation curves under different λ |
根据仿真曲线，可得到仿真数据见表 2.
| λ | 飞行时间 /s | 脱靶量 /m | 落角偏差 /(°) |
| 0.8 | 24.73 | 1.060 7 | 0.175 8 |
| 1.3 | 25.63 | 0.252 7 | 0.011 6 |
| 1.8 | 26.31 | 0.196 9 | 0.001 4 |
由仿真结果可知，随着λ的增加，弹道曲线被拉高，飞行时间逐渐增长，脱靶量减小，由于角度误差项系数占的比重逐渐增加，落角偏差减小. 当λ逐渐增加时，会致使导弹初始段的加速度增大，不利于导弹的控制. 因此，λ的取值定为1.3.
(2) 开关项系数ε
由式(8)可知，ε的大小影响系统滑模的趋近速率，各系数取值范围见表 3.
| 角度误差项系数λ | 开关项系数ε和趋近律系数k | 常值量δ |
| λ≥1.3 | ε，k>0 | δ>0 |
令k=1.0，δ=0.01，观察ε取不同值对系统的影响，其仿真结果如图 3所示.
 |
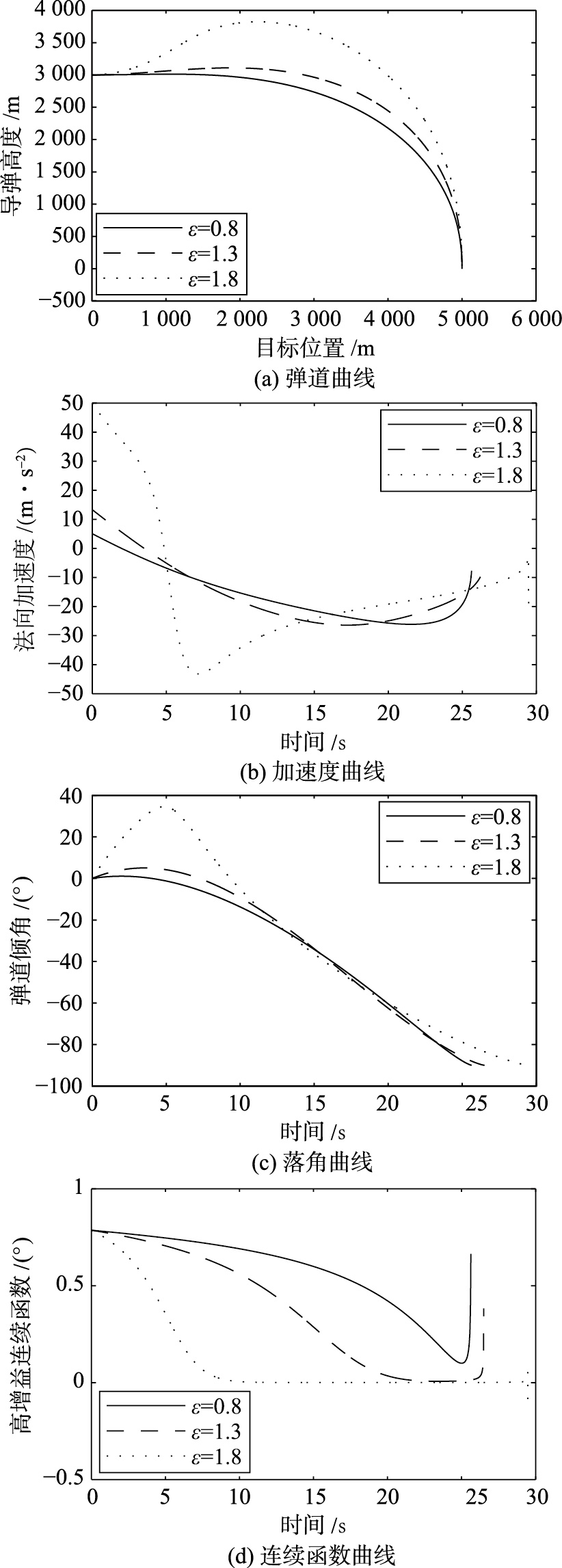| 图 3 ε不同取值下的仿真曲线Fig. 3 he simulation curves under different ε |
根据仿真曲线，可得到仿真数据见表 4.
| ε | 飞行时间 /s | 脱靶量 /m | 落角偏差 /(°) |
| 1 | 25.63 | 0.252 7 | 0.011 6 |
| 10 | 26.50 | 0.645 0 | 0.003 5 |
| 50 | 29.48 | 1.807 2 | 0.059 7 |
由仿真结果可知，随着ε的增加，导弹姿态变化加剧，飞行时间相应增长，落角偏差逐渐减小，脱靶量逐渐增加. 由于ε的增加，可以驱使系统加快趋近滑模面，但却使切换函数在末端产生较大波动，导致脱靶量的增加. 因此，ε的取值定为1.
(3) 趋近律系数k
k的取值影响系统滑模面的趋近速率，各系数取值范围见表 5.
| 角度误差项系数λ | 开关项系数ε和趋近律系数k | 常值量δ |
| λ≥1.3 | ε，k>0 | δ>0 |
令δ=0.01，观察k取不同值对系统的影响，其仿真结果如图 4.
 |
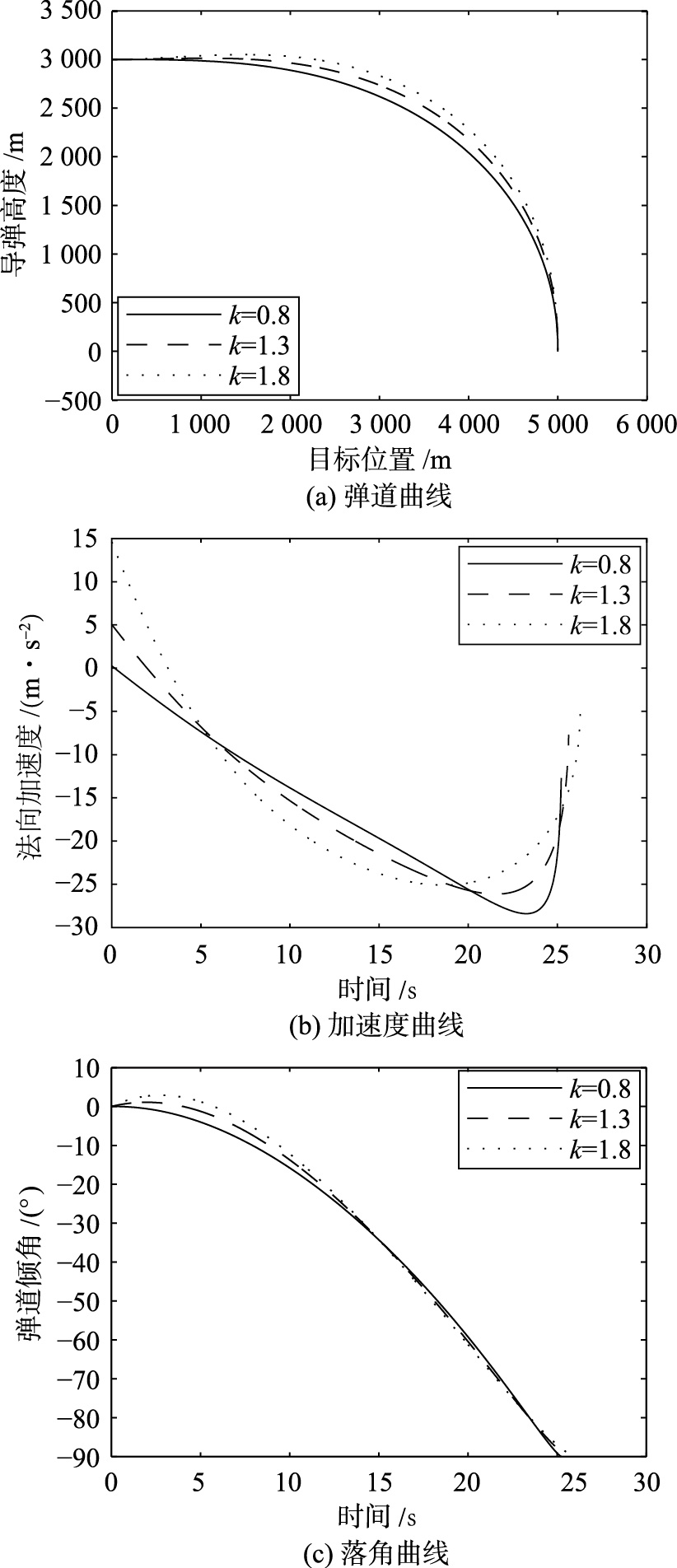| 图 4 k不同取值下的仿真曲线Fig. 4 The simulation curves under different k |
根据仿真曲线，可得到仿真数据见表 6.
| k | 飞行时间 /s | 脱靶量 /m | 落角偏差 /(°) |
| 0.5 | 25.22 | 1.646 8 | 0.015 1 |
| 1.0 | 25.63 | 0.252 7 | 0.011 6 |
| 1.5 | 26.29 | 1.804 6 | 0.004 2 |
由仿真结果可知，随着k的增加，落角偏差逐渐减少，飞行时间增长，脱靶量呈现先减小后增加的现象. 当k值较小时，系统到达滑模面的速率较慢，甚至当导弹接近目
标时，系统仍然没有趋近滑模面； 当k值较大时，系统可以快速到达滑模面，与此同时，导弹的法相加速度变得越来越大，致使导弹姿态发生变化，故k值过大或过小都会影响脱靶量的大小. 因此，k的取值定为1.
(4) 常值量δ
由式(9)可知，δ的取值影响高增益连续函数，根据工程经验，δ取值越小越好，令k=1、 λ=1.3、 ε=1，观察δ取不同值对系统的影响，其仿真结果如图 5所示.
 |
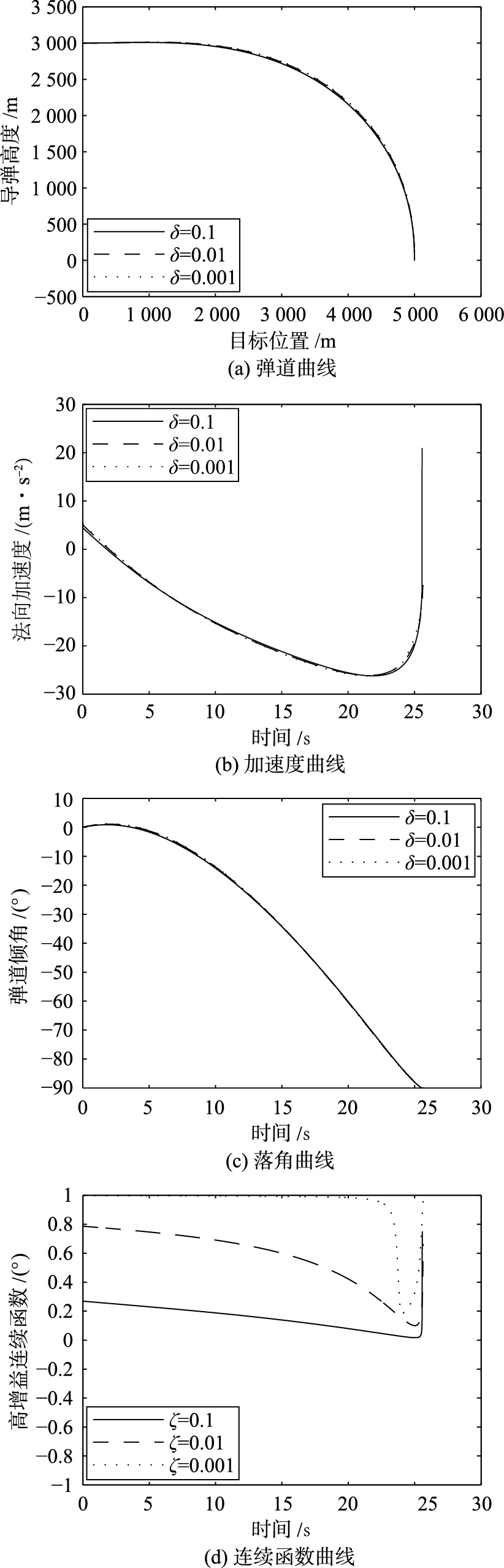| 图 5 δ不同取值下的仿真曲线Fig. 5 The simulation curves under different δ |
根据仿真曲线，可得到仿真数据见表 7.
| δ | 飞行时间 /s | 脱靶量 /m | 落角偏差 /(°) |
| 0.1 | 25.57 | 1.669 3 | 0.076 1 |
| 0.01 | 25.63 | 0.252 7 | 0.011 6 |
| 0.0001 | 25.67 | 2.416 7 | 0.003 2 |
由仿真结果可知，δ的大小对弹道曲线和末端落角影响很小，但对高增益连续函数的影响很大. 由于δ的减小，高增益连续函数趋向于0的速度会减慢，脱靶量和落角偏差相应减小. 但是，当δ很小时，高增益连续函数在末端出现严重的抖振，令导弹在末端时刻姿态出现偏差，导致脱靶量增加. 因此，δ的取值定为0.01.
通过上述讨论可以得到：
(1) 开关项系数ε和趋近律系数k的变化决定了系统自适应滑模趋近律中趋近速率的快慢和趋近滑模的质量，直接影响制导律脱靶量的大小.
(2) 角度误差项系数λ的大小影响切换函数中角度误差项的权重，导致制导律末段落角误差变化.
(3) 常值量δ的取值直接影响高增益连续函数.
4.3 仿真结果下面通过Matlab仿真软件对本文设计的带有末端落角约束的滑模变结构制导律进行仿真验证. 假设投放条件： 导弹初始位置(0，3 000)，初始视线角为0，导弹速度VM=260 m/s，初始弹道倾角θM=0°，期望以垂直角度命中位于(5 000，0)处的静止目标，且落点约束Rtf=0 m，落角约束qtf=-90°，仿真步长0.01 s.
根据4.1节制导参数的分析，取k=1，λ=1.3，ε=1，δ=0.01，图 6和表 8分别给出了滑模变结构制导律与比例导引律的仿真对比曲线和仿真对比数据.
 |
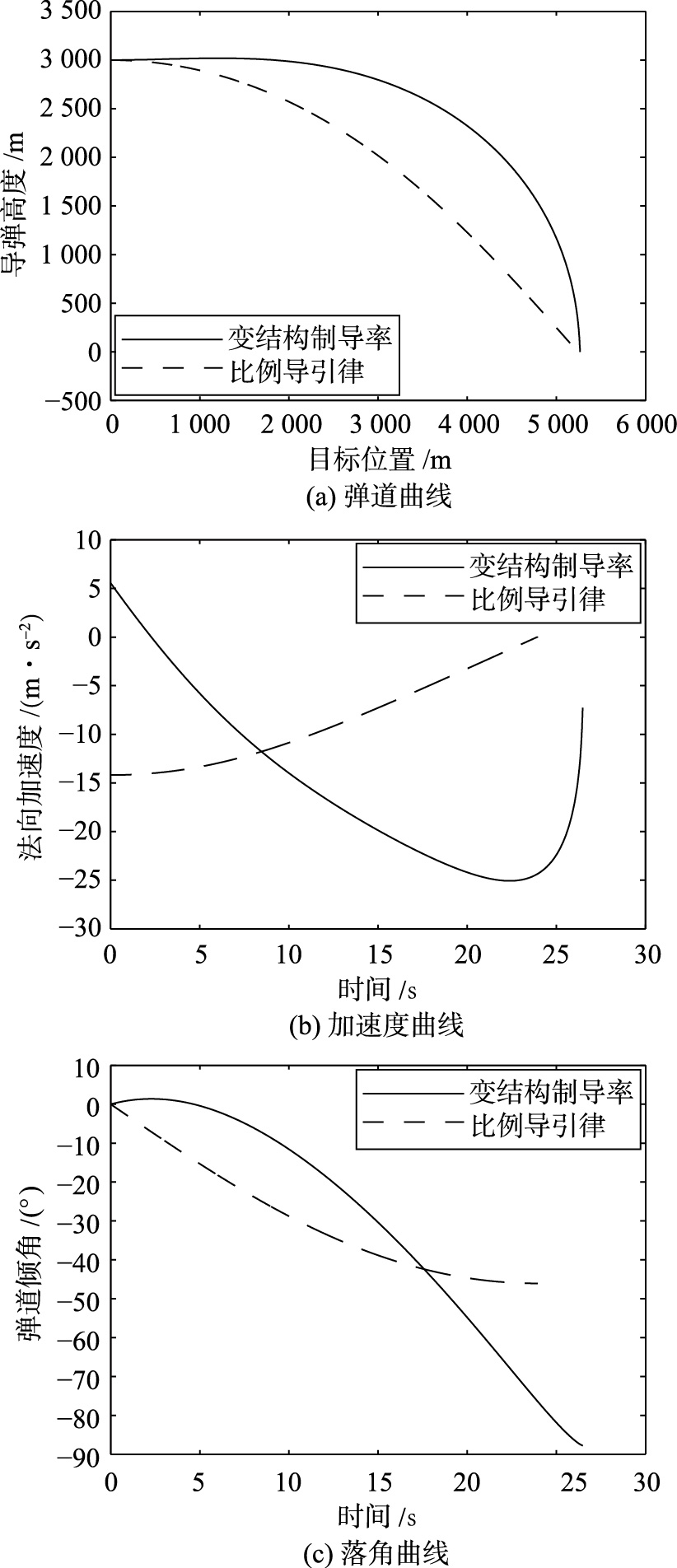| 图 6 制导性能对比仿真曲线Fig. 6 Simulation curves of guidance performance comparisons |
| 制导律 | 飞行时间 /s | 脱靶量 /m | 落角偏差 /(°) |
| 滑模变结构制导律 | 25.63 | 0.252 7 | 0.011 6 |
| 比例导引律 | 23.18 | 2.011 8 | 42.310 7 |
根据仿真对比曲线，可得到仿真数据见表 8.
将带有落角约束的滑模变结构制导律和优化的比例导引律进行仿真对比，可以得到两者的飞行时间分别为25.63 s和23.18 s，脱靶量为0.252 7 m和2.011 8 m，落角偏差为0.011 6°和42.310 7°. 虽然两种制导律的弹道曲线均较为平滑，但由于滑模变结构制导律的弹道曲线曲率较大，故飞行时间较长. 实际上，较高曲率的弹道曲线可以为导弹提供更快的速度，增强毁伤效果. 与改进的比例导引律相比，本文设计的制导律制导精度更高，可以达到期望落角，几乎以垂直角度命中目标.
5 结论(1) 建立了末端落角和视线角之间的关系，将落角约束转化成视线角的控制问题，降低了制导律设计难度.
(2) 结合脱靶量和落角约束条件，设计了一种空地导弹滑模变结构制导律. 针对实际系统中存在的不连续、 时滞等情况，采用高增益连续函数代替原有的符号项函数，有效地削弱了自适应滑模趋近律在滑模面的频繁切换而引起的抖振.
(3) 针对地面固定目标，分析了所设计的制导律中角度误差项系数λ、 开关项系数ε、 趋近律系数k和常值量δ等参数的相互影响，得到了4个制导参数的取值范围，为制导参数的选取提供了理论依据.
(4) 仿真结果证明，滑模变结构制导律满足脱靶量和落角控制要求，与比例导引律相比，脱靶量减少87.43％，末端落角增加47.01％.
在本文设计过程中，将目标加速度视为干扰量，如何精确估计目标信息，将作为下一步研究的重点.
| [1] | 孙未蒙, 刘湘洪, 郑志强. 多约束条件下的制导律研究综述[J]. 飞行力学, 2010, 28(4): 1-4. Sun W M, Liu X H, Zheng Z Q. Survey on the developments on the guidance law with impact angular constraints[J]. Flight Dynamics, 2010, 28(4): 1-4. |
| [2] | 蔡洪, 胡正东, 曹渊. 具有终端角度约束的导引律综述[J]. 宇航学报, 2010, 31(2): 315-332. Cai H, Hu Z D, Cao Y. A survey of guidance law with terminal impact angle constraints[J]. Journal of Astronautics, 2010, 31(2): 315-332. |
| [3] | 水尊师, 周军, 葛致磊, 等. 基于预测控制的角度约束制导律设计[J]. 飞行力学, 2011, 29(3): 56-59. Shui Z S, Zhou J, Ge Z L, et al. Guidance with impact angle constraint based on predictive control[J]. Flight Dynamics, 2011, 29(3): 56-59. |
| [4] | Rantnoo A, Ghose D. State dependent Riccati equation based guidance law for impact angle constrained trajectories[J]. Journal of Guidance, Control and Dynamics, 2009, 32(1): 320-325. |
| [5] | 张运喜, 孙明玮, 陈增强. 滑模变结构有限时间收敛制导律[J]. 控制理论与应用, 2012, 29(11): 1413-1418. Zhang Y X, Sun M W, Chen Z Q. Sliding-mode variable structure finite-time convergence guidance law[J]. Control Theory and Applications, 2012, 29(11): 1413-1418. |
| [6] | 马飞, 曹泽阳, 刘晖. 基于主从递阶决策模型的地空导弹混编群火力运用策略[J]. 信息与控制, 2010, 39(6): 755-760. Ma F, Cao Z Y, Liu H. Firing application strategies of ground-to-air missile composite group based on stackelberg decision model[J]. Information and Control, 2010, 39(6): 755-760. |
| [7] | Lee J, Min B M, Min J T. Suboptimal guidance laws with terminal jerk constraint[C]//International Conference on Control, Automation and Systems. Piscataway, NJ, USA: IEEE, 2007: 1399-1403. |
| [8] | Ryoo C K, Cho H J, Tahk M J. Optimal guidance laws with terminal impact angle constraint[J]. Journal of Guidance, Control, and Dymamics, 2005, 28(4): 724-732. |
| [9] | Jeon I S, Lee J I, Tahk M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-267. |
| [10] | Chen R H, Speyer J L, Lianos D. Optimal intercept missile guidance strategies with autopilot lag[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1264-1272. |
| [11] | 刘晓东, 吴云洁, 张武龙, 等. 导弹电动舵机系统离散自适应全程滑模控制[J]. 信息与控制, 2013, 42(4): 449-456. Liu X D, Wu Y J, Zhang W, et al. Discrete adaptive global sliding mode control for missile electromechanical actuator system[J]. Information and Control, 2013, 42(4): 449-456. |
| [12] | 陈兴林, 花文化. 具有终端约束的地面目标拦截比例导引[J]. 弹道学报, 2010, 22(2): 15-18. Chen X L, Hua W H. Ground target interception proportional navigation law with terminal constraints[J]. Journal of Ballistics, 2010, 22(2): 15-18. |
| [13] | Ryoo C K, Cho H J, Tahk M J. Time-to-go weighted optimal guidance with impact angle constraints[J]. IEEE Transactions on Control Systems Technology, 2006, 14(3): 483-492. |
| [14] | Song J M, Zhang T Q. Passive homing missile's variable structure proportional navigation with terminal angular constraint[J]. Chinese Journal of Aeronautics, 2001, 14(2): 83-87. |
| [15] | 于进勇, 唐大全, 顾文锦. 基于变结构控制理论的航向平面导引规律设计[J]. 飞行力学, 2005, 23(1): 50-53. Yu J Y, Tang D Q, Gu W J. Yaw plane guidance law design based on variable structure control theory[J]. Flight Dynamics, 2005, 23(1): 50-53. |
| [16] | Jung B, Kim Y.Guidance laws for anti-ship missile using impact angle and impact time[C]//AIAA Guidance, Navigation, and Control Conference.Keystone, CO, USA: AIAA, 2006: 3048-3060. |
| [17] | Koray S E, Osman M.Indirect impact angle control against stationary targets using biased pure proportional navigation[J].Journal of Guidance, Control and Dynamics, 2012, 35(2): 700-704. |
| [18] | Kim B S, Lee J G, Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-287. |
| [19] | 朱国栋, 林辉, 王琛.LS-SVM在线误差补偿的导弹自适应逆控制律设计[J].东南大学学报: 自然科学版, 2012, 42(S1): 15-19.Zhu G D, Lin H, Wang C.Adaptive inverse control law design of missile based on LS-SVM online error compensation[J].Journal of Southeast University: Natural Science Edition, 2012, 42(S1): 15-19. |
| [20] | 周荻.寻的导弹新型导引规律[M].北京: 国防工业出版社, 2002.Zhou D.New guidance laws for homing missiles[M].Beijing: National Defense Industry Press, 2002. |