2. 天津理工大学自动化系, 天津 300384
2. Department of Automation, Tianjin University of Technology, Tianjin 300384, China
1 引言
在现代军用和民用飞机应用领域中,复杂的动力学特性和各类影响因素常常会造成事故,影响飞行品质. PIOs(pilot induced oscillations or pilot in-the-loop oscillations),即飞行员诱发振荡,是在飞行过程中,飞行员的操纵与飞机性能及其外部环境严重不协调时出现的一种不可控的、 灾难性的、 不符合意愿的人机耦合振荡事件[1, 2]. 这种振荡降低了飞行品质,严重时会导致机毁人亡,造成不可逆转的损失[3].
通常,根据PIOs现象的线性与非线性程度,将PIOs分成三种类型[4]:
Ⅰ型PIOs: 线性的人—机系统耦合振荡,多是由时间延迟或滤波器造成的相位滞后以及飞行员的不当操作造成. 这种系统比较简单,容易预防.
Ⅱ型PIOs: 准线性的人—机系统耦合振荡,由舵面速率限制或位置限制等非线性因素而产生,这类PIOs的模型常被简化为式(1)所示形式.

Ⅲ型PIOs: 非线性耦合振荡,影响因素较多,但发生概率低并难以识别,且大多由Ⅱ型转化而来,一般不做研究.
针对Ⅱ型PIOs的分析与预防已有一些较为成熟的方案. 比如描述函数法和开环起始点(open loop onset point,OLOP)准则[5, 6, 7, 8]. 其中描述函数法是在频域内用描述函数来分析系统中非线性速率限制环节对Ⅱ型PIOs发生的影响. OLOP准则以描述函数方法为基础,针对选定的模型及输入参数等,计算Nichols图中严重相位跳跃的起始点[9]. 近年又提出一种同样基于描述函数法的Gap准则[10, 11],它基于正弦输入/三角输出的速率限制模型、 改进的尼尔—史密斯飞行员模型及飞机传递函数模型计算准则数,在Nichols图上进行分析,来预测纵向Ⅱ型PIOs. 另外,针对速率限制器饱和引发的相位滞后现象,国内外也有研究采用死区增稳(dead area stability augmentation,DASA)[12],速率限制反馈(rate-limited feedback,RLF)等方法进行补偿,利用连续信号法对控制系统产生连续的补偿信号,从而减弱附加时延.
虽然上述方法已取得很大成效,但它们大多侧重于分析或降低PIOs发生的可能性,不能从根本上预防PIOs的发生. MPC方法,是一种可处理约束的较成熟的控制方法,针对执行器幅值和速率饱和的系统,将饱和条件作为约束条件处理可取得较好的控制效果[13]. Ⅱ型PIOs发生的根本原因是速率限制器的饱和,因此,本文将速率饱和条件作为MPC方法的约束条件进行处理,保证输入信号在饱和限值内,从而克服速率限制器的影响,从根本上预防Ⅱ型PIOs的发生.
2 Ⅱ型PIOs现象及MPC方法 2.1 Ⅱ型PIOs产生的原因为了保护机械设备性能,飞行过程中,负载过多的情况下,一般使用速率限制器来保护飞机的执行器. 其结构框图如图 1所示.
 |
| 图 1 速率限制器框图Fig. 1 Rate limiter block diagram |
url、 yrl为速率限制器的输入及输出,L为速率限制值,-L、 L分别是输入限制的最小值和最大值. 对于正弦输入信号,当输入速率超出限制器的限值时,会引起输出信号幅值降低和相位滞后(如图 2所示). 相位滞后会造成系统的反馈与飞行员操作量之间产生偏差与时间延迟,使得飞行员无法及时准确判断,再加上信号的幅值降低,极易导致反复过分操作,从而引发PIOs的发生.
 |
| 图 2 速率限制器输入输出对比Fig. 2 Comparison of rate limiter input and output |
MPC方法3个核心部分: 模型预测、 滚动优化和反馈校正. 与其它控制方法相比,MPC方法能够针对多种预测模型进行分析,考虑系统的约束条件,并在有限时域内进行滚动优化[14, 15].
设一个离散线性定常系统具有如下形式:

要求满足约束条件:
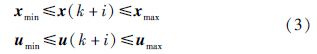
MPC控制器在当前采样时刻k的输出值由如下最优控制问题给出:
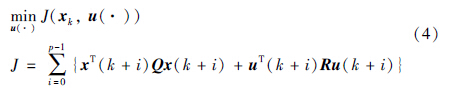

在下一个采样时刻k+1,系统基于新的测量状态xk+1重复(4)、 (5)的过程.
3 MPC控制器 3.1 MPC控制器设计如图 3所示,假设x1、 x2为可测量的状态变量,若速率限制器的影响能被克服,并忽略MPC控制器的作用,则y1=y2,x1=x2.
 |
| 图 3 MPC控制器框图Fig. 3 MPC controller diagram |
因此,设计一个MPC控制器,如虚线框内所示,用以将x1与x2的偏差最小化,即控制器新的状态为x2-x1. kp表示增益飞行员模型,A/F为所选飞机模型,虚线框内为控制器内部模型,外部的为实际系统被控对象.
控制器内部飞机模型定义为

控制器外部飞机模型定义为

于是MPC控制器可定义为

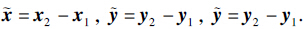
同时,将速率限制条件(1)转换为离散值:

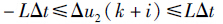 相应有:
相应有: 
于是,控制器(8)式可重写为


比较(10)式与(8)式,可知:

相应的最优控制如下:

要求满足约束条件:

 3.2 MPC控制器对系统相位的影响
3.2 MPC控制器对系统相位的影响 系统中飞机模型[16]的传递函数选为

本文中假设速率限制条件为


为了分析MPC控制器对系统相位的影响,取正弦信号为系统输入信号,在三种情况下进行对比分析(如图 4): 假设输入信号直接作用于飞机,输出为y1; 输入信号经过速率限制器作用于飞机,输出为y3; 输入信号通过控制器、 速率限制器作用于飞机,其输出为y2.
 |
| 图 4 正弦输入系统分析框图Fig. 4 Diagram of system analysis with sinusoidal input |
输入信号的幅值为a,频率ω取值从1到4(rad/s),频率变化幅度0.5(rad/s).
分别针对aω=11(°/s)和aω=12(°/s)两种情况进行仿真,在每种情况下,速率限制器均被激活,y2与y3分别与y1进行相位相减,相位差的对比结果如图 5所示.
 |
| 图 5 相位分析图Fig. 5 Phase analysis diagram |
可以看出,MPC控制器作用下所对应的两条曲线在0值上方,说明y2相对于y1相位超前,而参考输出y3所对应的两条曲线位于0值下方,显然相对y1相位滞后.
4 系统仿真为进一步探索MPC控制器对PIOs的抑制作用,针对图 3所示系统进行仿真. 当飞机处在一个极限振荡环节时,飞行员动作常被看作一个定常增益[17]. 因此,飞行员模型选为定常增益Kp.
同时,为了更清楚地突显MPC控制器的作用,将y3(速率限制器作用下飞行员操纵系统的输出)也加入对比. 假设系统初始值y0=5°,分别就kp=0.5与kp=1.15两种不同的飞行员增益,基于Matlab平台[18]进行编程仿真,俯仰角的仿真结果示于图 6和图 7.
 |
| 图 6 Kp=0.5时系统输出y1(飞行员直接控制),y2(飞行员+MPC控制器+限制器)和y3(飞行员+限制器)Fig. 6 Output y1 (only pilot),output y2(pilot+MPC controller+rate limiter),output y3(pilot with rate limiter) when Kp=0.5 |
 |
| 图 7 Kp=1.15时系统输出y1(飞行员直接控制),y2(飞行员+MPC控制器+限制器)和y3(飞行员+限制器)Fig. 7 Output y1 (only pilot),output y2(pilot+MPC controller+rate limiter),output y3(pilot with rate limiter) when Kp=1.15 |
图 6结果显示,系统没有发生振荡,三种情况下均可使系统快速趋于平衡状态. 但可以明显看出,y1与y2曲线基本重合,而由飞行员和速率限制器共同作用时的系统响应y3,即使最终达到稳定,输出值仍然存在些许控制误差.
当增益Kp增大时,逐渐接近临界PIOs发生点,为便于清晰分析,三种系统输出分别示于图 7.
图 7显示: 当增益稍大时,由飞行员直接控制虽然能够恢复到平衡状态,但在初始阶段会发生高频率大幅值的振荡,且持续时间较长(图 7(a)),这将会严重损害机械设备的性能,同样威胁到飞行安全; 而飞行员在有速率限制器时进行操作,飞机会发生严重的振荡现象即PIOs(图 7(c)); 加入MPC控制器的系统,则可以快速恢复到平衡状态(图 7(b)).
5 结论将模型预测控制方法应用于防止PIOs的发生是一种新的尝试,并且计算机技术的发展也为其应用提供了可能.
OLOP法、 描述函数法等多侧重于分析PIOs发生的可能性,而本文利用MPC方法在计算系统输入时能够处理约束的优势,将速率限制条件转化为系统约束条件进行考虑,从而将输入信号变化率控制在饱和范围内,克服了速率限制器的影响,从根本上杜绝PIOs的发生. 仿真结果表明,MPC控制器能克服速率限制器引起的相位滞后(图 5); 系统未发生振荡时,可以减小飞行员操作误差(图 6); 在可能发生振荡条件下,MPC控制器能够有效抑制PIOs的发生(图 7).
| [1] | Liang X H, Yamada K, Sakamoto N, et al. Model predictive controller design to suppress rate-limiter-based pilot-induced oscillations[J]. Japan Society of Aeronautical Space Sciences Transactions, 2007, 49(166): 239-245. |
| [2] | 管萱. 飞行员诱发振荡(PIO)的研究[D]. 南京: 南京航空航天大学, 2010. Guan X. Research on pilot induced oscillations(PIO)[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010. |
| [3] | Duda H. Prediction of pilot-in-the-loop oscillations due to rate saturation[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(3): 581-587. |
| [4] | 刘继权, 豆国辉. 基于速率限制的Ⅱ型飞行员诱发振荡评估方法[J]. 航空工程进展, 2012, 3(4): 427-432, 441. Liu J Q, Dou G H. Prediction methods of category Ⅱ pilot induced oscillations due to actuator rate limiting[J]. Advances in Aeronautical Science and Engineering, 2012, 3(4): 427-432, 441. |
| [5] | Liebst B S, Chapa M J, Leggett D B. Nonlinear prefilter to prevent pilot-induced oscillations due to actuator rate limiting[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(4): 740-747. |
| [6] | Henley J G. A comparison of nonlinear algorithms to prevent pilot-induced oscillations caused by actuator rate limiting[D]. Maxwell, AL, USA: Air University, 2003: 1-84. |
| [7] | 孟捷, 徐浩军, 武卫. 飞行员模型对Ⅱ型PIO预测影响研究[J]. 系统仿真学报, 2009, 21(12): 3816-3819. Meng J, Xu H J, Wu W. Research on prediction of category Ⅱ PIO affected by pilot model[J]. Journal of System Simulation, 2009, 21(12): 3816-3819. |
| [8] | 李富刚, 田福礼. 基于舵机速率限制的PIO探测与抑制技术研究[J]. 飞行力学, 2013, 31(2): 170-174. Li F G, Tian F L. Detection and suppression research of PIO induced by actuator rate limiting[J]. Flight Dynamics, 2013, 31(2): 170-174. |
| [9] | 吴蔚, 方振平. 某电传操纵飞机的Ⅱ型PIO预测和抑制对策研究[J]. 航空学报, 2002, 23(3): 231-233. Wu W, Fang Z P. Analysis and prediction of pilot-induced-oscillation with actuator rate limiting of a fly-by-wire fighter and a method for alleviating PIO[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(3): 231-233. |
| [10] | 朱广东, 李颖晖, 李雪松, 等. GAP准则在飞行员诱发振荡预测中的应用[J]. 火力与指挥控制, 2012, 37(7): 10-13. Zhu G D, Li Y H, Li X S, et al. Application f GAP criterion on prediction of pilot induced oscillations[J]. Fire Control & Command Control, 2012, 37(7): 10-13. |
| [11] | 李琳, 陈云翔, 李千, 等. 基于改进差分进化算法的 PIO预测评估方法[J]. 飞行力学, 2014, 32(1): 74-77. Li L, Chen Y X, Li Q, et al. Prediction and evaluation method for PIO based on modified differential evolution[J]. Flight Dynamics, 2014, 31(1): 74-77. |
| [12] | 孟捷, 徐浩军, 张建康. Ⅱ型PIO反馈与前馈抑制系统对比[J]. 航空学报, 2010, 31(9): 1701-1707. Meng J, Xu H J, Zhang J K. A comparison of feedback and foreback schemes to prevent category ⅡPIO[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(9): 1701-1707. |
| [13] | Kapila V, Valluri S. Model predictive control of systems with actuator amplitude and rate saturation[C]//Proceedings of the 37th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 1998: 1396-1401. |
| [14] | 杨圆圆. 模型预测控制研究与应用[D]. 大庆: 大庆石油学院, 2006. Yang Y Y. A study on the theories and applications of model predictive control[D]. Daqing: Daqing Petroleum Institute, 2006. |
| [15] | 袁新宇. 模型预测控制及其应用研究[D]. 杭州: 浙江大学, 2002. Yuan X Y. Studies on model predictive control and its application[D]. Hangzhou: Zhejiang University, 2002. |
| [16] | Liang X H. Model predictive controller design to suppress rate-limiter-based pilot induced oscillations[D]. Nagoya: Nagoya University, 2006. |
| [17] | McRuer D T. Pilot-induced oscillations and human dynamic behavior[M]. Washington, USA: NASA, 1995. |
| [18] | 丛爽, 邓娟. MATLAB环境下的模型预测控制理论的应用[J]. 计算机工程与应用, 2005, 41(16): 196-198, 212. Cong S, Deng J. Model predictive control theory and application under MATLAB environment[J]. Computer Engineering and Applications, 2005, 41(16): 196-198, 212. |



