1 引言
随着航天科学技术的发展越来越快,对其技术要求也越来越高,航天器的姿态控制与稳定得到了密切的关注和广泛的研究. 近些年来,国内外许多学者在该领域取得了大量的研究成果,如反馈控制、 最优控制、 自适应控制、 滑模控制等及其综合控制方法[1, 2, 3, 4, 5, 6, 7]. 这些非线性控制方法都具有一定的优越性,被广泛应用到航天器控制中. 周端等[8]研究了具有模型参数不确定和环境干扰的挠性航天器姿态大角度快速机动控制的高维多目标优化问题. 朱敏等[9]针对太阳帆航天器的薄膜帆面和大尺度杆的柔性特征,建立了太阳帆航天器非线性刚柔耦合动力学模型,虽然它们能保证闭环控制系统的稳定,但是得到的只是系统在平衡点处的渐近稳定,稳定时间是无穷的. 从控制系统时间优化的角度来看,保证控制系统有限时间收敛的控制方法才是时间最优的控制方法. 由于有限时间控制器中带有分数幂项,使得有限时间闭环控制系统与非有限时间闭环系统相比具有更好的鲁棒性能和抗扰动能力,使其在航天器姿态控制系统中也得到了广泛的研究[10, 11]. 在现有的研究成果中,大多数控制方法只能保证当时间趋于无穷时系统收敛于平衡点; 而有限时间控制方法,在某种程度上说具有响应速度快、 控制精度高和干扰抑制等特性.
对于闭环系统连续有限时间稳定性的研究与证明,主要基于两大判据: (1) 李亚普诺夫稳定性定理,其中包括终端滑模及其变形,如非奇异终端滑模、 快速终端滑模、 双幂次快速终端滑模,主要运用到普通的有限时间定理、 扩展有限时间定理等. (2) 齐次性理论方法. 文[12]针对地球轨道的主从航天器动态协同编队控制问题,建立了一个6自由度的相对运动模型,然后提出一类基于终端滑模技术的控制器保证了动态协同误差在有限时间内收敛到期望的轨迹. 文[13]针对使用单位四元数描述的刚体航天器系统的姿态跟踪问题,设计了2种有限时间控制器保证姿态控制系统对期望姿态的有限时间可达性,但是其设计的控制器存在奇异值现象. 针对该标准终端滑模控制的奇异值问题,文[14]在此基础上进行了改进,提出了一类新颖的、 无奇异的终端滑模控制方案,实现了姿态跟踪控制系统的有限时间稳定.
基于齐次性理论方法的有限时间稳定性研究在航天领域的应用比较少,这是一个新的研究热点,引起了众多学者的关注和重视. 针对仅有位置测量信息的空间机器臂控制系统,文[15]提出了一类结合期望重力补偿和连续的输出反馈PD(proportional-differential)控制,来解决其全局有限时间调节问题,并基于李亚普诺夫定理和齐次性有限时间定理证明了系统的稳定性. 此外,文[10]针对刚体卫星姿态控制问题,设计了存在和不存在外干扰力矩两种条件下有限时间状态反馈控制律; 其中针对无扰动情形,基于非线性齐次系统性质,设计了一种类PD控制的反馈控制算法,保证姿态闭环控制系统的有限时间收敛到平衡点,该方法结构简单且便于应用于工程实践. 文[16]对刚体卫星的有限时间姿态稳定问题进行了研究,基于齐次性方法,设计了一类局部连续饱和有限时间控制器保证闭环系统的有限时间稳定; 基于一个切换函数,设计了一类全局有限时间控制器,遗憾的是设计过程中并没有考虑外部干扰摄动对闭环系统的影响.
本文考虑在轨刚体航天器姿态稳定控制系统存在参数不确定性等问题,航天器姿态控制系统通过引入自适应状态变量转换为单个级联系统,并将有限时间理论设计基于融入奇次理论的航天器姿态稳定控制器. 该有限时间控制器结构简单、 便于调节,具有很高的实际工程实用价值.
2 系统模型及预备知识 2.1 航天器姿态动力学与运动学方程航天器姿态的运动学描述方法有方向余弦、 欧拉角、 四元数、 罗德里格参数和修正的罗德里格参数(MRPs). 因为四元数描述能用最少的参数表示航天器运动姿态且全局无奇异,故本文采用四元数来描述航天器的姿态运动学:
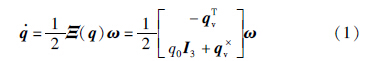
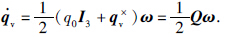
此处,定义叉乘(·)×为一个斜对称矩阵,也就是说针对一个3维向量σ=σ1; σ2; σ3,σ×表示为
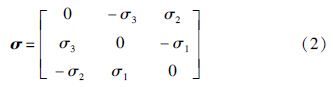
考虑航天器姿态动力学方程:

假设1 干扰力矩d是未知但有界的,即存在一个正常数d0使d0成立,d0是未知干扰力矩的上界.
实际上,航天器的转动惯量是不可确切知道的,也就是说在轨航天器的转动惯量J与其标称值J0间存在一定的不确定有界差值ΔJ,也即J=J0+ΔJ. 由此,航天器的姿态动力学方程可以重新描述为
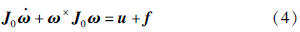
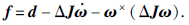
假设2 对任意t>0,存在q0(t)≠0.
由上定义的Q(qv)=q0I3+q×v可知,det(q=q0. 因此,通过此假设可知,矩阵Q(qv)是非奇异的,也即ω= 非奇异. 由此,系统方程式(1)和式(4)可重构为
非奇异. 由此,系统方程式(1)和式(4)可重构为

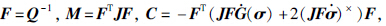
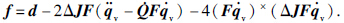
假设3 航天器转动惯量的不确定值ΔJ是未知有界的,由此f是未知但有界的,且存在一个正常数f0使 f0成立.
f0成立.
航天器的等价系统方程式(5)具有如下的重要性质:
性质1 矩阵M是一个对称的正定矩阵,且 是一个斜对称矩阵,即满足
是一个斜对称矩阵,即满足

性质2 矩阵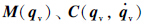 都是有界的,即存在正常数cMmax>cMmin>0和cCmax>cCmin>0,使得
都是有界的,即存在正常数cMmax>cMmin>0和cCmax>cCmin>0,使得
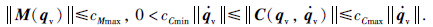
为了便于有限时间姿态控制系统的设计,基于非线性系统稳定性和有限时间稳定性给出如下定义和引理.
考虑如下非线性自治系统:

定义1 如果系统(6)的平衡点x=0,在领域U⊂U0内,式(6)是李亚普诺夫稳定和有限时间稳定的,则其是局部有限时间稳定. 有限时间稳定,也即存在一个函数T∶U\{0}→(0,∞),针对∀x0∈U⊂Rn,系统(6)的解为sf(x0)=0,当t∈[0,T(x0))时,sf(x0)∈U\{0}; 当t>T(x0)时, 特别地,若U⊂Rn,则系统(6)是全局有限时间稳定.
特别地,若U⊂Rn,则系统(6)是全局有限时间稳定.
定义2[17] 考虑如下非线性系统:


引理1[18] 考虑如下系统:


此外,如果系统(9)是全局渐近稳定的且是局部有限时间稳定的,那么该系统就是全局有限时间稳定.
引理2(Barbalat引理)[19] 设φ∶R→R是[0,∞)上的一致连续函数,假设 存在且有限,则
存在且有限,则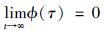 成立.
成立.
引理3[20] 假设f(t):R+→R是一个可微函数并满足:
1)  存在并有限;
存在并有限;
2) 存在两个函数g1(t)和g2(t)满足

若g1(t)是一致连续函数且满足 ,那么
,那么 成立.
成立.
为了便于控制系统的设计与分析,定义向量Tanh(∈),sig(∈)α∈Rn,对角矩阵Sech(∈)∈Rn×n如下:
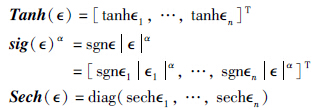
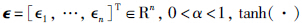 和sech(·)分别表示标准的双曲正切和双曲正割函数,sgn(·)表示标准的符号函数,diag(·)表示一个标准的非零对角矩阵. 根据以上定义,可以容易得到以下结论:
和sech(·)分别表示标准的双曲正切和双曲正割函数,sgn(·)表示标准的符号函数,diag(·)表示一个标准的非零对角矩阵. 根据以上定义,可以容易得到以下结论:
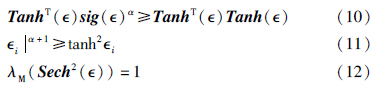
此处为了便于姿态控制系统的描述与分析,定义x=

Step 1: 首先,给出李亚普诺夫函数:


若选择适当的参数k1>0,ρ>0,cMmax>0和0<α <1使满足:
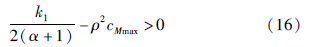
将式(15)代入式(14),针对x=[x1,x2,x3]T≠0有:

对式(14)定义的李亚普诺夫函数求导有:

此时,给出如下的控制方案:
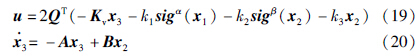
将式(19)和式(20)代入式(18)有:

由假设1和3,以及性质2知, 和
和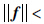 f0都是有界的,此处定义
f0都是有界的,此处定义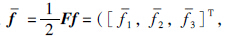 则存在
则存在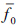 满足
满足 由此得:
由此得:
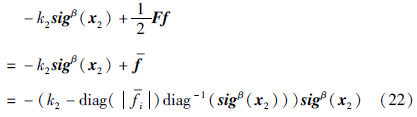
若选择适当的参数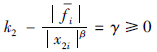 使得k2-
使得k2- 为正定矩阵,也即此时x2被控制在边界层
为正定矩阵,也即此时x2被控制在边界层 以内,则有:
以内,则有:

根据文中假设和函数方程性质,则有:

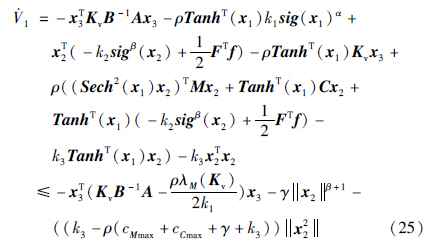
如果选择适当的参数满足如下条件:

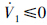 ,且当满足x3=x2=0时,
,且当满足x3=x2=0时,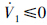 . 由李亚普诺夫稳定性定理和Lasalle引理可得,航天器姿态控制系统式(13)在控制器式(19)和式(20)的作用下,若选取适当的参数满足式(26)和式(27),则系统是渐近稳定的.
. 由李亚普诺夫稳定性定理和Lasalle引理可得,航天器姿态控制系统式(13)在控制器式(19)和式(20)的作用下,若选取适当的参数满足式(26)和式(27),则系统是渐近稳定的. Step 2: 在这一部分,要证明当系统式(13)参数不确定性f=0时局部有限时间稳定. 首先,对式(13)进行变换:
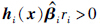
根据引理1,定义: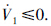
 则上式可变为
则上式可变为

由此,易知上式的一个标准系统:

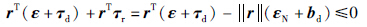 的齐次系统. 其中,
的齐次系统. 其中,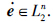 则根据引理1有:
则根据引理1有:
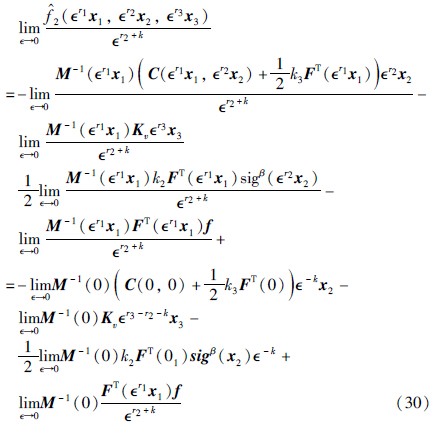
若参数不确定性f=0,则式(30)可以变为

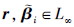
同理,可以得到:

因此,由引理1可以得到,当参数不确定性f=0时,航天器姿态控制系统是局部有限时间稳定的. 由此,给出如下定理.
定理 针对姿态控制系统式(13),在假设1~3的限制下,采用有限时间控制器式(19)和式(20)的作用下,选取适当的参数满足式(26)和式(27)时,系统是渐近稳定的; 当参数不确定性f=0时,航天器姿态控制系统能达到局部有限时间稳定.
证明 见上文Step 1和Step 2,此处略.
4 仿真与分析为了验证本文提出的有限时间控制器(FTC)的有效性,利用Matlab/Simulink软件,对航天器姿态机动控制过程进行仿真研究,航天器主要参数和控制器仿真参数如表 1所示. 另假设作用在航天器的外部干扰力矩为

| 项目名称 | 参数 |
|
航天器 模型参数 | 转动惯量J=[20 0 0.9; 0 17 0; 0.9 0 15] kg·m2 初始姿态q(0)=[0.9; -0.3; 0.26; 0.18] 初始角速度ω(0)=[0.3; -0.25; -0.3] rad/s |
|
有限时间 控制器 (FTC) | k1=1.8,k2=1.2,k3=2.6,α=0.8 |
|
PID 控制器 | β=0.86 Kv=diag(1 1.2 2),A=diag(1 1 1),B=diag(1 1 1) KP=3.2,KI=0.000 5,KD=4.0 |
在上述的模型的参数下,为了进行比较,本部分对本文设计的有限时间控制器(FTC)和传统的经典PID控制进行仿真,以验证本文方案的有效性和优越性.
针对存在干扰力矩的情况,对本文的控制器和传统的PID控制器进行了仿真比较. 图 1和图 2给出了航天器系统姿态和姿态角速度的时间响应曲线. 在本文提出的控制器FTC(实线)的控制下,航天器姿态控制系统能在8 s内达到稳定,并具有10-4量级的高稳定精度,保证了闭环控制系统的稳定; 此外本文设计的控制器也体现对外部干扰有效的抑制能力,从航天器姿态的时间响应曲线图 2可以看出,姿态虽然出现波动,但幅值和频率较小. 在PID(点线)控制器的作用下,系统的稳定时间在20 s以上,且稳定精度只有10-3,在外部干扰的作用下,航天器的姿态也有较大的摄动和稳态误差. 图 3给出的无干扰情况下控制器提供的力矩的时间响应曲线. 由此可见,即使在存在外部干扰的情况下,本文实际的FTC控制能保证姿态控制的有限时间稳定,并具有很好的优越性.
 |
| 图 1 有干扰情况下姿态四元数q的时间响应Fig. 1 Time responses of the attitude quaternion q with disturbance |
 |
| 图 2 有干扰情况下姿态角速度ω的时间响应Fig. 2 Time responses of the attitude angular velocity ω with disturbance |
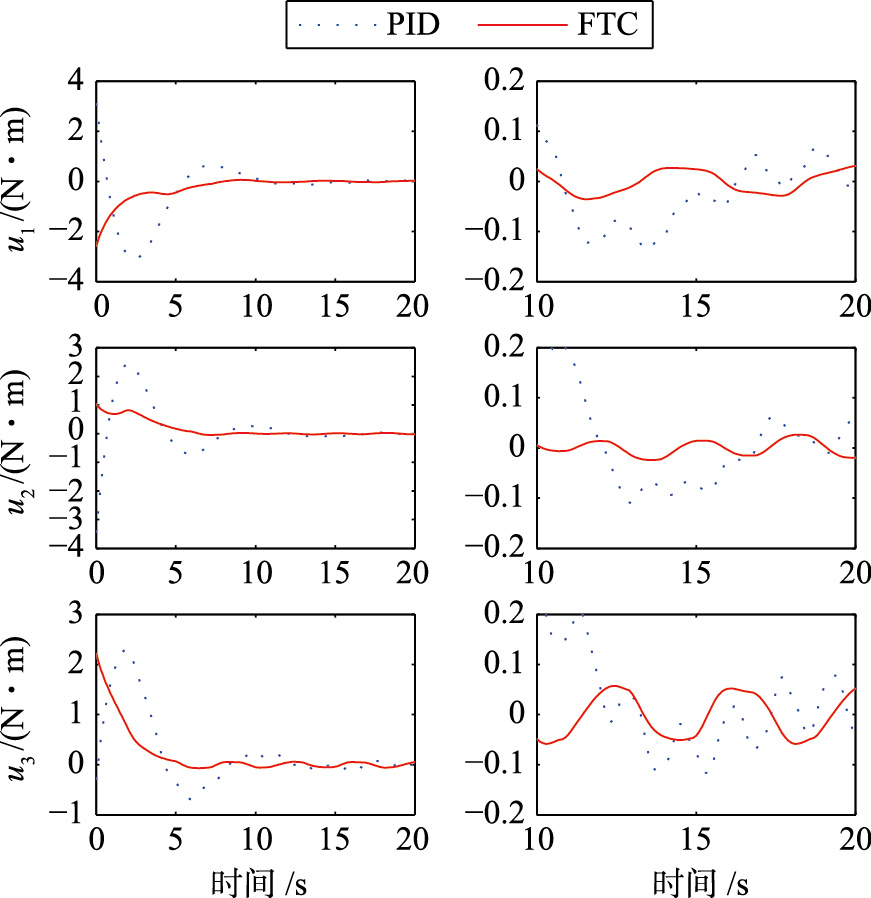 |
| 图 3 有干扰情况下控制器力矩u的时间响应Fig. 3 Time responses of the control torques u with disturbance |
针对存在参数不确定性的航天器姿态稳定控制系统,提出了一类基于奇次性理论的有限时间姿态控制器. 首先,通过引入新的自适应状态变量,将航天器姿态控制系统转换为一个级联系统; 然后,基于齐次性的理论方法,设计了一类新颖的有限时间渐近稳定控制器,并利用李亚普诺夫理论,证明了系统在存在参数不确定性时的渐近稳定性及不存在参数不确定性时闭环系统有限时间稳定性. 最后,将提出的算法应用于某刚体航天器姿态稳定控制任务中,数字仿真结果验证了方案的有效性和可行性. 本文设计的有限时间控制器结构简单,便于调节,具有很高的实际工程实用价值. 但是,本文研究局限于局部有限时间稳定,对于航天器姿态控制系统的全局有限时间稳定控制器的设计与论证,将是下一步工作的难点与重点.
| [1] | Yin S, Ding S, Xie X, et al. A review on basic data-driven approaches for industrial process monitoring[J]. IEEE Transactions on Industrial Electronics, 2015, 61(11): 6418-6428. |
| [2] | 宋斌, 李传江, 马广富. 航天器姿态机动的鲁棒自适应控制器设计[J]. 宇航学报, 2008, 29(1): 121-125. Song B, Li C J, Ma G F. Robust adaptive controller design for spacecraft during attitude maneuver[J]. Journal of Astronautics, 2008, 29(1): 121-125. |
| [3] | 李波, 胡庆雷, 石忠, 等. 考虑执行器安装偏差时航天器姿态稳定的控制分配[J]. 宇航学报, 2013, 34(1): 25-31. Li B, Hu Q L, Shi Z, et al. Dynamic control allocation for attitude stabilization of spacecraft considering actuator misalignment[J]. Journal of Astronautics, 2013, 34(1): 25-31. |
| [4] | Hu Q, Ma G, Xie L. Robust and adaptive variable structure output feedback control of uncertain systems with input nonlinearity[J]. Automatica, 2008, 44(2): 552-559. |
| [5] | Xin M, Pan H. Integrated nonlinear optimal control of spacecraft in proximity operations[J]. International Journal of Control, 2010, 83(2): 347-363. |
| [6] | Lu K, Xia Y, Zhu Z, et al. Sliding mode attitude tracking of rigid spacecraft with disturbances[J]. Journal of the Franklin Institute: Engineering and Applied Mathematics, 2012, 349(2): 413-440. |
| [7] | Yin S, Li X, Gao H, et al. Data-based techniques focused on modern industry: An overview[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 657-667. |
| [8] | 周端, 陈庆伟, 胡维礼, 等. 挠性航天器姿态机动控制的高维多目标优化[J]. 信息与控制, 2013, 42(3): 299-308. Zhou D, Chen Q W, Hu W L, et al. A high dimensional multi-objective optimization of attitude maneuver control for flexible spacecraft[J]. Information and Control, 2013, 42(3): 299-308. |
| [9] | 朱敏, 张洋, 卫一恒, 等. 太阳帆航天器姿态动力学建模与反馈线性参数变化控制[J]. 信息与控制, 2013, 42(2): 196-201. Zhu M, Zhang Y, Wei Y H, et al. Attitude dynamic modeling and feedback LPV control of solar sail[J]. Information and Control, 2013, 42(2): 196-201. |
| [10] | 李贵明, 刘良栋. 刚体卫星姿态的有限时间控制[J]. 空间控制技术与应用, 2011, 37(3): 1-8. Li G M, Liu L D. Finite rime stabilization method for the rigid spacecraft attitude control[J]. Aerospace Control and Application, 2011, 37(3): 1-8. |
| [11] | Hu Q, Li B, Zhang A. Robust finite-time control allocation in spacecraft attitude stabilization under actuator misalignment[J]. Nonlinear Dynamics, 2013, 73(1/2): 53-71. |
| [12] | Wang J, Liang H, Sun Z, et al. Finite-time control for spacecraft formation with dual-number-based description[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 950-962. |
| [13] | Jin E, Sun Z. Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control[J]. Aerospace Science and Technology, 2008, 12(4): 324-330. |
| [14] | Li S, Wang Z, Fei S. Comments on the paper: Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control[J]. Aerospace Science and Technology, 2011, 15(3): 193-195. |
| [15] | Su Y, Zheng C, Müller P C. Global continuous finite-time output feedback regulation of robot manipulators[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2008: 3383-3388. |
| [16] | Du H, Li S. Finite-time attitude stabilization for a spacecraft using homogeneous method[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 740-748. |
| [17] | Rosier L. Homogeneous Lyapunov function for homogeneous continuous vector field[J]. Systems and Control Letters, 1992, 19(6): 467-473. |
| [18] | Hong Y, Xu Y, Huang J. Finite-time control for robot manipulators[J]. Systems and Control Letters, 2002, 46(4): 243-253. |
| [19] | Khalil H K, Grizzle J. Nonlinear systems[M]. 3rd ed. Upper Saddle River, NJ, USA: Prentice-Hall, 2002: 303-334. |
| [20] | Dawson D M, Zergeroglu E, Behal A, et al. Nonlinear control of wheeled mobile robots[M]. Berlin, Germany: Springer-Verlag, 2001: 156-157. |



