1 引言
因老年人身体运动机能下降和交通事故等原因，使步行功能障碍患者逐年增多. 根据运动康复治疗原理，对患者有针对性的康复训练能够帮助其恢复运动功能. 为缓解医护资源不足并降低医护人员的负担，利用康复机器人为患者提供康复训练的需求不断增多[1, 2]. 由于康复机器人应用对象的特殊性，保证康复者的安全极为重要.
目前对康复步行训练机器人所设计的控制器都是建立在系统能产生足够快的运动速度去跟踪医生指定的训练路径[3, 4, 5]的基础上的. 康复步行机器人与其它机械系统[6, 7, 8, 9]等需要较快跟踪速度去实现控制目标不同，其主要应用对象是步行障碍患者，如果以较快速度跟踪医生指定轨迹，会导致患者跟不上机器人的运动速度. 因患肢的稳定性较差，容易使患肢再次受到伤害，对康复者来讲，不限制康复步行训练机器人的运动速度是不安全的. 从实际应用角度考虑，康复步行训练机器人不能以无限制速度对康复者进行训练，因此需要对其运动速度进行限制. 而一旦速度受到限制，会使系统的跟踪性能遭到破坏，甚至使系统失去稳定性. 如何设计速度受限型控制器，使系统达到渐近稳定并保证跟踪性能具有重要意义.
本文针对全方向康复步行训练机器人(OmniDirectional rehabilitative training Walker，ODW)[10]，研究速度受限的轨迹跟踪控制问题. ODW存储医生的计划训练路径，患者只需跟随ODW运动便可实现全方向锻炼. 针对系统存在的不确定性，文[11, 12]通过鲁棒控制方法实现了轨迹跟踪； 为了克服不同体重患者对轨迹跟踪精度的影响，文[13, 14]设计自适应控制器实现了轨迹跟踪. 然而，这些控制方法都没有对ODW的运动速度进行限制，而当ODW的运动速度受到限制时，必然会增大跟踪误差，上述控制方法因不能分别对轨迹跟踪误差和速度跟踪误差进行单独补偿而具有一定的局限性.
Backstepping技术是一种有效的非线性系统控制方法[15, 16, 17]，对于严反馈结构的非线性系统，通过调整每步虚拟控制器参数，可以提高系统跟踪精度和性能[18]. 当ODW的运动速度受到限制时，常规Backstepping控制方法会增大轨迹跟踪误差. 如何在控制器中引入补偿项，保证系统的稳定性和轨迹跟踪是速度受限型控制器设计成功的关键.
本文提出一种具有误差补偿的Backstepping速度受限型控制器设计方法，通过分别对轨迹跟踪误差和速度跟踪误差实时补偿，以消除速度受限后对系统产生的不良影响，弥补已有康复步行训练机器人的控制方法没有考虑速度受限的不足； 基于李亚普诺夫稳定性理论和LaSalle不变性原理，证明了补偿误差系统和跟踪误差系统的渐近稳定性； 与常规Backstepping控制方法进行了对比分析，验证了速度受限型控制器设计方法的有效性和误差补偿设计的优越性，该控制方法能保证康复者在安全速度下进行康复训练.
2 ODW动力学模型ODW的结构坐标图如图 1所示.
 |
| 图 1 全方向ODW结构坐标图Fig. 1 Structure of omnidirectional ODW |
其中：
∑(x，O，y)表示全局坐标系；
∑(x′，C，y′)表示平移坐标系；
v表示ODW的步行速度；
vi表示ODW每个轮子的速度，i=1，2，3，4；
fi表示ODW每个轮子的输入力；
L表示ODW的中心到每个轮子的距离；
li表示ODW的重心到每个轮子中心的距离；
r0表示ODW中心到重心的距离；
α表示x′轴和速度v之间的夹角；
β表示x′轴和r0之间的夹角；
θi表示x′轴和每个轮子对应的L之间的夹角；
φi表示x′轴和每个轮子对应的li之间的夹角.
系统动力学模型描述如下[19]：
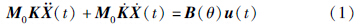
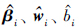
针对动力学模型(1)，令：
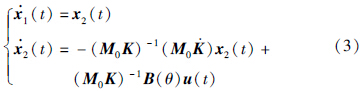
为保证康复者在安全速度下进行康复训练，设速度幅值受限函数为SR(x)，其定义如下：
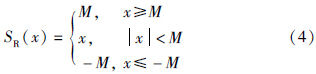
定义1 对于全方向康复步行训练机器人系统(1)，设跟踪运动速度为x2(t)，其中xT2(t)=xx2(t)xy2(t)xθ2(t)，xx2(t)、 xy2(t)分别表示x、 y轴方向的运动速度，xθ2(t)表示旋转角速度； 设系统允许的最大运动速度为vmax，其中vTmax=[vxmax vymax vθmax]，vxmax、 vymax分别表示x、 y轴方向的最大运动速度，vθmax表示最大旋转角速度. 当系统运行时，总有
成立，称x2(t)是系统的安全运动速度.
定义2 对于全方向康复步行训练机器人系统(1)，在安全运动速度下设计控制器u(t)，使系统达到渐近稳定并实现控制目标，称u(t)为速度受限型控制器.
本文研究的主要目的是针对系统(1)，设计速度受限型控制器u(t)，在ODW不超过系统允许的最大运动速度vmax前提下，使系统达到渐近稳定并实现轨迹跟踪.
3 速度受限型控制器设计设Xd(t)表示医生指定的训练轨迹，X(t)ODW实际的运动轨迹，控制器的设计分为如下两步：
Step 1： 定义轨迹跟踪误差：
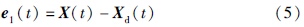
对式(5)求导并根据式(2)得
对式(6)设计如下虚拟速度控制信号：
定义如下轨迹补偿误差项：
Step 2： 定义速度跟踪误差：
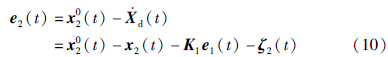
对式(10)求导得
对式(11)设计如下控制输入信号：
定义如下速度补偿误差项：
将式(14)和式(15)代入控制器U(t)，得到具有轨迹补偿误差项ξ1(t)和速度补偿误差项ξ2(t)的控制器如下：
将式(17)代入式(16)得
进一步，通过式(18)和式(12)得到如下含有补偿项ξ1(t)、 ξ2(t)的速度受限型控制器：
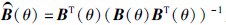为B(θ)的广义逆矩阵. 4 稳定性分析
接下来，对系统的稳定性进行分析.
定理 考虑由式(1)描述的全方向康复步行训练机器人系统，设系统初始状态有界，指定的跟踪轨迹及一阶导数连续且有界，那么在式(19)所示的速度受限型控制器作用下，补偿误差系统式(8)和式(14)渐近稳定； 进一步，轨迹跟踪误差e1(t)和速度跟踪误差e2(t)渐近稳定.
证明 首先，对式(5)和式(10)求导，并根据式(7)和式(3)得
其次，对轨迹补偿误差项式(8)求导，并根据式(20)和式(9)得
对速度补偿误差项式(10)求导，并根据式(21)和式(15)得
最后，根据补偿误差项建立李亚普诺夫函数：
对式(24)沿式(22)和式(23)求导，得
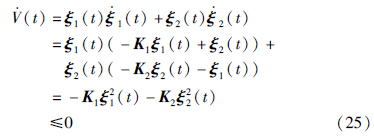
事实上，V·(t)=0意味着ξ1(t)=0且ξ2(t)=0，即：
根据LaSalle不变性原理，Θ中仅有零解. 因此，补偿误差系统式(8)和式(14)渐近稳定.
进一步，由式(15)可知，当t→∞，有ζ2(t)→0，又知ξ2(t)→0，从而根据式(14)可知，e2(t)→0. 再由式(9)可知，当t→∞，有ζ1(t)→0，进而根据式(8)可知，e1(t)→0，于是可知轨迹跟踪误差e1(t)和速度跟踪误差e2(t)渐近稳定.
说明1 常规Backstepping控制方法可以实现ODW的轨迹跟踪，但如果ODW跟踪速度受到限制，必然会加大轨迹跟踪误差，使ODW不能跟踪指定的运动轨迹，因此需要对常规Backstepping控制方法增加补偿，以消除速度受限后产生的轨迹跟踪误差.
说明2 文中提出了轨迹跟踪误差和速度跟踪误差补偿项的设计方法，该设计方法不仅能实现补偿误差系统的渐近稳定，而且可以保证整个跟踪误差系统的渐近稳定.
5 仿真结果为了验证文中提出控制器设计方法的有效性，基于ODW动力学模型，对医生指定的直线训练轨迹进行了跟踪，直线方程描述如下：
仿真研究中，ODW的物理参数为
ODW进行步行训练的最快运动速度v=0.25 m/s，这样在实际康复训练过程中，当ODW沿坐标轴方向运动，将得到ODW的最大运动速度vmax在x轴、 y轴方向受限范围为-0.25 m/s≤vx≤0.25 m/s，-0.25 m/s≤vy≤0.25 m/s. 文中将在ODW运动速度vx、 vy约束的范围内，实现训练轨迹跟踪，因医生指定的跟踪角度θd(t)较小，康复者依靠前臂扶板支撑身体，ODW运动时的旋转角速度对康复者来讲是安全的，因此针对这一训练轨迹，对旋转角速度不进行限制. 初始条件xc(0)=0 m，yc(0)=0 m，θc(0)=0.75 rad，控制器参数矩阵为K1=diag｛0.18，0.19，1.8｝，K2=diag｛1.0，0.8，10｝，仿真结果如图 2～图 7所示.
 |
| 图 2 x轴轨迹跟踪Fig. 2 Trajectory tracking of x axis |
 |
| 图 3 y轴轨迹跟踪Fig. 3 Trajectory tracking of y axis |
 |
| 图 4 方向角轨迹跟踪Fig. 4 Trajectory tracking of orientation angle |
 |
| 图 5 25 s内直线路径跟踪Fig. 5 Path tracking of line in 25 s |
 |
| 图 6 ODW速度受限Fig. 6 ODW with velocity constraints |
 |
| 图 7 直线路径跟踪Fig. 7 Path tracking of line |
由图 2～图 4可知，ODW能快速跟踪方向角，而在初始约25 s内，x轴、 y轴方向产生较大的轨迹跟踪误差，使ODW不能跟踪训练路径，如图 5所示. ODW运动速度受限情况下，如图 6所示，当轨迹跟踪误差和速度跟踪误差得到实时补偿后，跟踪误差逐渐减小，系统达到渐近稳定，最终实现了对指定训练轨迹的完全跟踪，如图 7所示.
为了进行对比分析，如果对康复步行训练机器人系统不设计速度受限型控制器，无需对跟踪误差进行补偿，可以直接利用常规Backstepping方法，控制器的设计过程如下：
对式(6)设计虚拟速度控制信号：
定义速度跟踪误差：
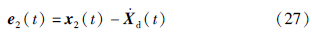
对式(27)求导，并将式(3)代入得
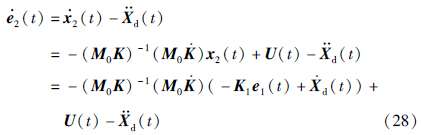
为了进一步说明文中速度受限型控制器补偿项设计的优越性，再对控制器式(29)作用下的康复步行训练机器人进行速度限制，通过仿真对比说明常规Backstepping控制方法必须增加补偿，才能消除速度受限后产生的轨迹跟踪误差.
设初始条件为
控制器参数矩阵为K1=diag｛80，90，80｝，K2=diag｛100，80，90｝，仿真结果如图 8～图 13所示.
 |
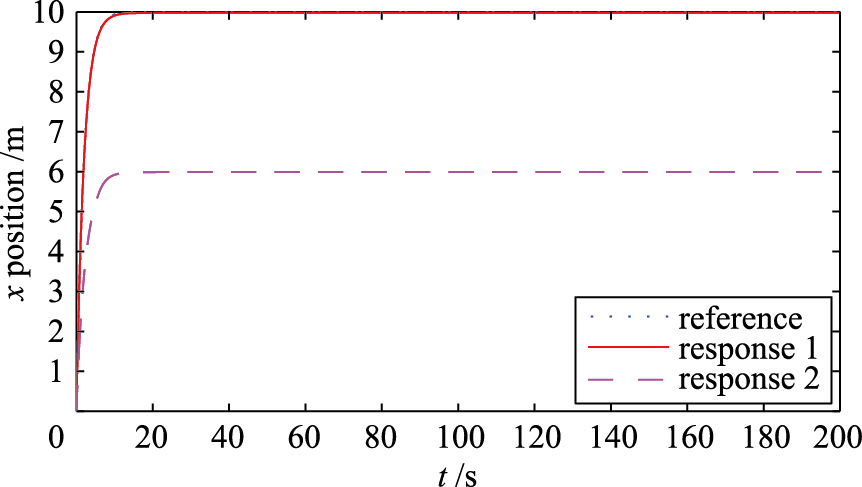| 图 8 x轴轨迹跟踪Fig. 8 Trajectory tracking of x axis |
 |
| 图 9 y轴轨迹跟踪Fig. 9 Trajectory tracking of y axis |
 |
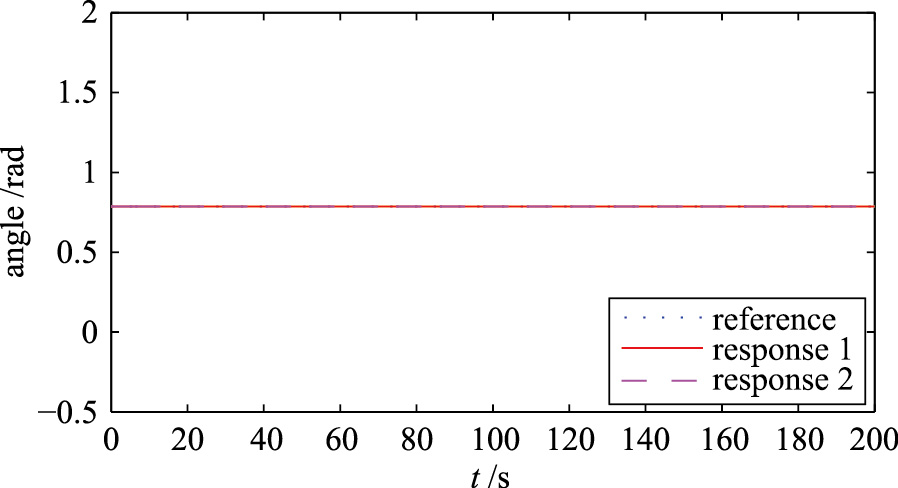| 图 10 方向角轨迹跟踪Fig. 10 Trajectory tracking of orientation angle |
 |
| 图 11 x轴运动速度Fig. 11 Motion speed of x axis |
 |
| 图 12 y轴运动速度Fig. 12 Motion speed of y axis |
 |
| 图 13 2阶PDF策略控制结构Fig. 13 theecondorder |
在控制器式(29)作用下，速度不受限制时轨迹跟踪用response 1表示，将其跟踪速度限制在安全速度范围内的轨迹跟踪用response 2表示. 由图 8、 图 9可以看出，当ODW速度不受限制时，能够完全跟踪医生指定的训练轨迹，而当速度受到限制时，因没有补偿项作用，导致x轴、 y轴方向产生较大的轨迹跟踪误差，并且这个跟踪误差一直未能消除. 因为没有限制ODW旋转角速度，方向角跟踪未受到影响，如图 10所示. 图 11、 图 12表明，在初始约15 s时间内，ODW在x轴、 y轴方向运动速度均超过0.25 m/s，并且最大速度已经达到了5 m/s，是最大安全速度的20倍，然后逐渐降到0.25 m/s趋于稳定，这个运动速度对康复者是极其危险的，因此为保证康复者安全训练，必须限制ODW的运动速度，x轴、 y轴方向受限后的运动速度vx1和vy1对康复者是安全的. 对直线路径的跟踪如图 13所示，速度未受到限制时，ODW能够完全跟踪指定路径，而一旦速度受到约束，ODW不但偏离直线路径，而且不能实现轨迹跟踪. 因此常规Backstepping控制方法速度受到限制时不能实现控制目标，必须通过增加补偿项，才能有效降低常规Backstepping控制方法的不足.
由定义1和定义2可知，文中提出的基于Backstepping补偿方法的速度受限型控制器，能使系统达到渐近稳定并实现轨迹跟踪. 对于医生指定的跟踪轨迹，其一阶导数代表了跟踪速度，考虑到康复者在实际锻炼中能承受的行走速度，往往使跟踪轨迹一阶导数的最值不超过x轴、 y轴方向的运动速度. 如果应用速度受限型控制器，不仅可以方便设计康复者的训练轨迹，而且能够保证康复者在安全速度下进行更多轨迹的康复训练.
6 结论研究了全方向康复步行训练机器人系统速度受限的轨迹跟踪控制问题. 提出了基于Backstepping补偿方法的速度受限型控制器设计方案，通过对轨迹跟踪误差和速度跟踪误差的实时补偿，实现了对指定训练路径的跟踪； 基于李亚普诺夫稳定性理论和LaSalle不变性原理，证明了系统的渐近稳定性； 仿真研究表明了文中提出控制器设计方法的有效性和误差补偿设计的优越性，所设计的控制器能保证康复者在安全速度下进行康复训练. 文中提出的速度受限型控制器设计方法，除了康复步行训练机器人以外，对于需要限速的轮式移动机器人均具有适用性.
| [1] | 潘礼正, 宋爱国, 徐国政, 等. 上肢机器人实时安全控制[J]. 机器人, 2012, 34(2): 197-203. Pan L Z, Song A G, Xu G Z, et al. Real-time safety control of upper-limb rehabilitation robot[J]. Robot, 2012, 34(2): 197-203. |
| [2] | Pan L Z, Song A G, Xu G Z, et al. Safety supervisory strategy for an upper-limb rehabilitation robot based on impedance control[J]. International Journal of Advanced Robotic Systems, 2013, DOI: 10.5772/55094. |
| [3] | Seo K, Lee J. The development of two mobile gait rehabilitation systems[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2009, 17(2): 156-166. |
| [4] | Ju M, Lin C K, Lin D H. A rehabilitation robot with force position hybrid fuzzy controller: Hybrid fuzzy control of rehabilitation robot[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2005, 13(3): 349-358. |
| [5] | Chugo D, Matsuoka W, Jia S. Rehabilitation walker system with standing assistance device[C]//Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation. Piscataway, NJ, USA: IEEE, 2007: 2177-2182. |
| [6] | Valenzuela M L, Santibanez V. Robust saturated PI joint velocity control for robot manipulators[J]. Asian Journal of Control, 2013, 15(1): 64-79. |
| [7] | Yang S X, Zhu A, Yuan G F, et al. A bioinspired neuodynamics-based approach to tracking control of mobile robots[J]. IEEE Transactions on Industrial Electronics, 2012, 59(8): 3211-3220. |
| [8] | Chwa D. Fuzzy adaptive tracking control of wheeled mobile robots with state-dependent kinematic and dynamic disturbances[J]. IEEE Transactions on Fuzzy systems, 2012, 20(3): 587-593. |
| [9] | Kolhe J P, Shaheed M, Chandar T S, et al. Robust control of robot manipulators based on uncertainty and disturbance estimation[J]. International Journal of Robust and Nonlinear Control, 2013, 23(1): 104-122. |
| [10] | Sun P, Wang S Y. Redundant input guaranteed cost switched training control for omnidirectional rehabilitative training walker[J]. International Journal of Innovative Computing, Information and Control, 2014, 10(3): 883-895. |
| [11] | Yang J Y, Chen X X, Guo H C. Implementation of omnidirectional lower limbs rehabilitation training robot[C]//Proceeding of International Conference on Electrical Machines and Systems. Piscataway, NJ, USA: 2007: 2033-2036. |
| [12] | 杨俊友, 白殿春, 王硕玉, 等. 全方向轮式下肢康复训练机器人轨迹跟踪控制[J]. 机器人, 2011, 33(3): 314-318. Yang J Y, Bai D C, Wang S Y, et al. Trajectory tracking control of omnidirectional wheeled robot for lower limbs rehabilitation[J]. Robot, 2011, 33(3): 314-318. |
| [13] | Tan R P, Wang S Y, Jiang Y L. Adaptive control method for path-tracking control of an omnidirectional walker compensating for center-of-gravity shifts and load changes[J]. International Journal of Innovative Computing, Information and Control, 2011, 7(7): 4423-4434. |
| [14] | Tan R P, Wang S Y, Jiang Y L, et al. Nonlinear adaptive controller for omnidirectional walker: Dynamic model improvement and experiment [J]. ICIC Express Letters, 2012, 6(3): 611-615. |
| [15] | Zhou J, Wen C Y, Yang G H. Adaptive Backstepping stabilization of nonlinear uncertain systems with quantized input signal[J]. IEEE Transactions on Automatic Control, 2014, 59(2): 460-464. |
| [16] | Ma R C, Dimirovski G M, Zhao J. Backstepping robust H∞control for a class of uncertain switched nonlinear systems under arbitrary switchings[J]. Asian Journal of Control, 2013, 15(1): 41-50. |
| [17] | 严浙平, 晏正新, 牟春晖, 等. 基于反步法的欠驱动UUV的3维路径跟踪控制[J]. 信息与控制, 2012, 41(2): 180-184. Yan Z P, Yan Z X, Mu C H, et al. 3D path following control of underactuated UUV based on Backstepping[J]. Information and Control, 2012, 41(2): 180-184. |
| [18] | Davila J. Exact tracking using Backstepping control design and high-order sliding modes[J]. IEEE Transactions on Automatic Control, 2013, 58(8): 2077-2081. |
| [19] | Tan R P, Wang S Y, Jiang Y L, et al. Adaptive controller for omnidirectional walker: Improvement of dynamic model[C]//Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation. Piscataway, NJ, USA: IEEE, 2011: 325-330. |