1 引言
在未知环境中,机器人的自定位与环境创建是机器人执行其它任务的基础. 机器人要根据带有噪声的传感器观测建立周围环境的地图,同时根据已建地图估计机器人在环境中的位姿. 多年来基于滤波的SLAM方法得到很大发展,常用的滤波方法包括扩展卡尔曼滤波(EKF)方法[1]、 扩展信息滤波(EIF)方法[2]及粒子滤波(PF)方法[3]等. 然而,基于滤波器的方法存在线性化及更新效率等问题,使得它难以应用于大规模环境的地图创建[4].
Lu与Milios首先提出基于图优化的SLAM方法(Graph SLAM)[5],然而受限于计算方法,无法满足实时性要求. 随着高效求解方法的出现,Graph SLAM成为当前SLAM研究的热点[6, 7, 8, 9]. 近年来,涌现了许多优秀的Graph SLAM算法,如TreeMap[6]、 TORO(tree-based network optimizer)[7]、 HOG-Man[8]及g2o[9]. 然而不可避免地,尽管有一些学者对Graph SLAM前端的闭环产生和闭环确认提出了改进方法[10, 11, 12],但仍然会不同概率地出现错误闭环,这些错误闭环使常规Graph SLAM算法不能收敛或者收敛到错误的结果. 在大范围闭合环境中剔除数据关联引入的错误闭环成为了机器人SLAM的一个必要功能,称为鲁棒闭环[13]. 为此,Latif[13]提出了利用闭环集群内部及外部的一致性检验来排除错误闭环的RRR(realizing,reversing,recovering)算法,但在大量错误闭环环境下算法耗费时间较长,实效性不好. Olson[14]采用一种多模态的高斯模型作为鲁棒的代价函数,为每个闭环添加一个无效假设,在优化过程中判定闭环是否有效,但在大量错误闭环环境下算法召回率较低. Sünderhauf[15]提出给每个闭环约束添加一个转换变量,控制约束对整个图的影响,在优化过程中调整机器人位姿和转换变量,使鲁棒的代价函数最小. 这种算法的关键是将闭环约束看作可转换的约束类型,因此称为SC(switchable constrain)算法. 然而此方法需要同时对两种参量进行优化,并手动设定一个常量,迭代次数较多.
针对以上问题,在Sünderhauf思想的基础上,本文提出一种自适应的鲁棒闭环代价函数. 通过分析鲁棒闭环代价函数中各项参数对优化过程的具体影响,确定代价函数中的转换变量、 原先需要手动设定的参量与其它可计算量的关系和计算方法,从而可以较好地运用于不同环境下的数据集,具有较强的自适应性.
2 鲁棒闭环Graph SLAM算法在Graph SLAM算法中,机器人位姿作为图中的节点,里程计约束以及闭环约束作为图中的边约束. 令X=(x1,…,xn)T为机器人位姿矩阵,xi为机器人在时刻i的位姿. 约束边为U={Uodom,Uloop}={umn},包括里程计约束Uodom={ukl}(l=k+1)及闭环约束Uloop={uij}. Graph SLAM图结构如图 1.
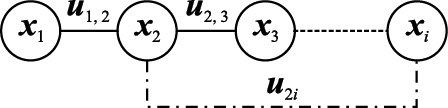 |
| 图 1 Graph SLAM图结构Fig. 1 The structure of Graph SLAM graph |
常规Graph SLAM算法由前端(front-end)和后端(back-end)组成,前端根据外部传感器输入的原始数据来确定图结构的节点位姿和边约束,后端则根据前端得到的节点和边信息,利用非线性最小二乘等方法对图结构进行优化,得到满足约束的最优节点位姿. Graph SLAM算法框架见图 2.
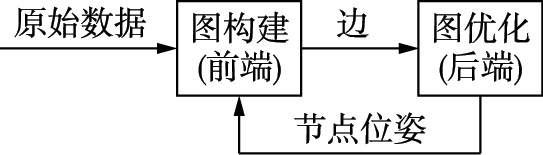 |
| 图 2 Graph SLAM算法框架Fig. 2 The structure of Graph SLAM algorithm |
令γmn和Σmn分别为从节点m到节点n的约束边umn的观测均值向量及协方差阵. 在给定节点状态x和边约束umn下计算约束边引入的剩余误差emn:
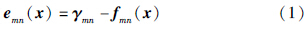
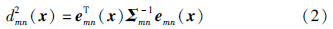
假定所有约束是独立的,得到所有边约束的引入误差为
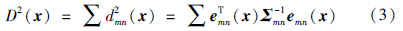
对于式(3),常规的Graph SLAM算法通常采用Gauss-Newton或Levenberg-Marquadt等非线性最小二乘方法,找到使所有边引入误差最小的节点X*:
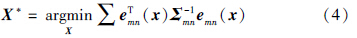
显而易见,当约束中存在错误闭环时,采用常规Graph SLAM算法完全考虑错误闭环对整个图优化的影响,必定会造成算法结果与真实情况相距甚远. 由此,Sünderhauf提出的SC算法,将里程计约束ukl与闭环约束uij分开考虑,从而得到里程计约束项和闭环约束项,并为闭环约束附加转换变量sij∈[0, 1],在优化过程中通过调整sij的大小以控制闭环约束对节点的影响,同时加入附加项w1-sij2以避免闭环约束误差项被完全消除,无法利用正确闭环修正机器人位姿[15]. SC算法思想如下式所示:
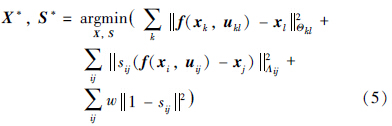
然而SC算法在优化过程中要同时对参量X和S进行迭代计算,而每次迭代过程中参量并非沿着误差最小方向发展,就需要多次迭代才能得到较优解. 另外,算法对于不同数据集中附加项设定的常量w也没有给出进一步的说明,只是采用多次实验的方法确定一个合适的w值,这在真实的未知环境的SLAM实验中并不现实. 在SC算法实验过程中发现,不同的w值对实验结果的准确性具有一定影响,甚至会导致算法收敛到错误结果. 因此得出结论,采用固定w值的SC算法无法得到最优效果.
3 具有自适应性的鲁棒闭环Graph SLAM算法由于SC算法没有利用数据集信息对算法内部的参量进行确定,算法不能很好地适应不同数据集的计算需求,导致算法收敛速度较慢,甚至不能收敛到正确的结果. 为进一步考虑代价函数中的转换变量s和常量w对算法效果的影响,单独对一个闭环边uab的约束项及其附加项进行分析,这里将式(5)改写为
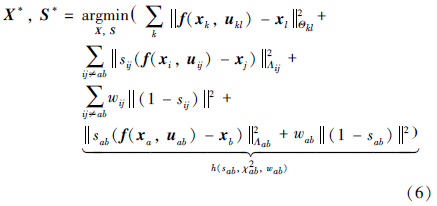
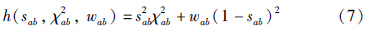
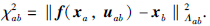
当式(6)取得最优解时,其代价函数关于所有s的偏导数为0,即对sab的偏导也为0. 由于代价函数中只有h含有sab项,因此其对转换变量sab的偏导数为0. 为具有一般性,下面省去下标ab,h对s求导,使其导数为0,得到此时s值为

在式(8)中,χ2可通过计算求得,w未知. 令χ′=‖f(xa,uab)-xb‖2,考虑到在优化过程中w与χ′、Λ具有一定联系,令w=g(χ′,Λ). 分析式(8)可知:

对g(χ′,Λ)中χ′的考虑: 当闭环正确时,此闭环约束应作为图优化的重要因素,在优化过程中得到重视,即其s值应趋近于最大值1,而此时通过计算得到的误差值χ′较小,因此s应与χ′保持负相关关系,见式(10),同样闭环错误时亦是如此:
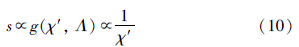
对g(χ′,Λ)中Λ的考虑: 当闭环正确时,s值应趋近于最大值1. 而对于一个正确闭环来说,其Λ值通常来说较小. 因此较大的Λ通过函数g(χ′,Λ)应计算得到较小的s值,即s与Λ为负相关关系,见式(11),同样对于错误闭环中的优化也是如此:
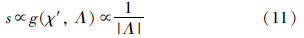
考虑到s与χ′、Λ存在的内在联系,这里采用以下函数计算w值:
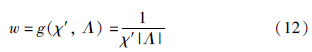

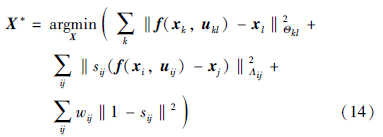
由此,得到了对每个闭环约束uij计算sij和wij的方法,使得算法只需对节点xij进行搜索. 通过在每次迭代中应用Λ和最新的χ2、 χ′对wij和sij的更新,动态地改变约束边对节点的影响,使正确闭环能够逐步矫正节点位置,并大大减弱错误闭环在整个优化过程中的影响力. 因此本文提出的算法可看作一种自适应的SC算法(ASC).
4 实验与分析为进行算法对比,对公开的数据集Manhattan3500、 City10000、 Bicocca进行仿真. 对于Manhattan3500合成数据集,采用初始位姿精度不同的Manhattan3500Olson[16]数据集和Manhattan3500g2o[9]数据集,以此检验初始位姿精度对算法收敛时间的影响. 从最后算法运行结果上看,两种数据集结果相似性较高. City10000合成数据集从iSAM功能包[17]中获得. Bicocca真实数据集从RRR[13]中获得. 4个数据集节点与边的个数见表 1,机器人真实节点图见图 3. 图 4为原始数据中机器人节点与边.
| 数据集 | 节点数 | 边个数 |
| City10000 | 10 000 | 20 687 |
| Bicocca | 8 358 | 8 405 |
| Manhattan_Olson | 3 500 | 5 598 |
| Manhattan_g2o | 3 500 | 5 598 |
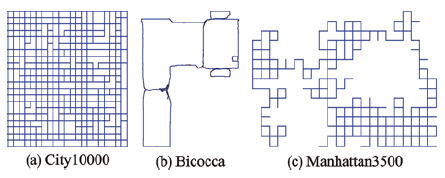 |
| 图 3 数据集节点真实位姿Fig. 3 True nodes′ poses of the datasets |
 |
| 图 4 数据集原始节点(蓝)与边(红)Fig. 4 Raw nodes (blue) and edges (red) of the datasets |
为了检验算法对前端产生的不同类型错误闭环的适应性,采用文[15]的方法对每个数据分别添加4种类型的异常闭环,即随机(random)闭环、 局部(local)闭环、 随机组(random grouped)闭环及局部组(local grouped)闭环. 随机闭环在图中随机选取2个节点添加约束边. 局部闭环随机在局部区域添加闭环. 组闭环则是添加具有一致性的若干闭环约束. 采用这4种闭环用于模拟在真实环境中可能出现的错误闭环. 这里使用Vertigo包[18]提供的添加异常闭环工具.
对数据集添加500个异常闭环约束后,利用常规Graph SLAM算法对含有异常闭环的数据集进行运算,得到节点和边的配置,如图 5. 可见常规的Graph SLAM算法对闭环依赖性高,一旦闭环错误就会导致灾难性后果. 因此有必要应用Graph SLAM的鲁棒闭环算法.
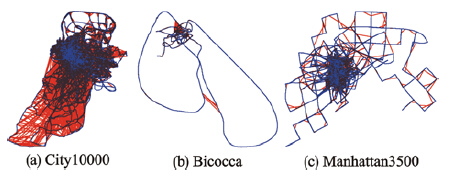 |
| 图 5 异常闭环结果节点(蓝)和边(红)Fig. 5 Nodes (red) and edges (blue) of the outliers result |
本文对4个数据集分别添加4种不同类型(R、 L、 RG、 LG)、 不同数量(1 000,2 000,3 000,4 000)的异常闭环. 采用SC算法和本文的ASC算法对数据集进行计算. 在SC算法中设定w=1[15]. 迭代优化时,代价函数变化量小于阈值时算法停止. 得到的两种算法的收敛时间见表 2. 由于两种算法得到的结果类似,这里给出在1 000个随机异常闭环下ASC算法得到的节点与边的结果,见图 6.
| 数据集 | 1 000 | 2 000 | 3 000 | 4 000 |
| 算法 | R,L,RG,LG | R,L,RG,LG | R,L,RG,LG | R,L,RG,LG |
| City10000_SC | 40.5,32.4,50.4,25.2 | 95.6,33.8,84.1,31.4 | 218.4,45.1,123.4,41.8 | 320.2,47.6,240.6,53.4 |
| City10000_ASC | 15.6,8.5,9.4,4.2 | 40.1,9.2,23.5,5.3 | 65.1,12.4,31.1,8.2 | 206.9,11.7,180.1,10.8 |
| Bicocca_SC | -,-,-,- | -,-,-,- | -,-,-,- | -,-,-,- |
| Bicocca_ASC | 2.1,0.9,1.7,1.0 | 2.5,1.1,2.4,1.4 | 3.7,1.7,3.4,1.3 | 5.1,2.7,6.8,2.4 |
| Manhattan_Olson_SC | 12.6,2.3,9.7,2.4 | 19.7,2.4,16.5,2.1 | 28.6,3.4,32.6,3.6 | 45.6,4.5,38.2,4.8 |
| Manhattan_Olson_ASC | 6.4,1.2,3.9,1.6 | 7.5,2.1,8.4,1.9 | 19.6,2.3,21.9,3.2 | 24.8,3.1,20.7,4.4 |
| Manhattan_g2o_SC | 3.8,1.7,3.5,1.2 | 7.6,2.6,4.5,2.8 | 9.4,3.2,11.2,5.1 | 12.6,3.4,12.1,6.7 |
| Manhattan_g2o_ASC | 2.1,1.1,2.3,0.9 | 4.5,1.7,3.2,1.6 | 6.5,1.9,5.7,2.6 |
8.4,2.2,7.5,4.1 |
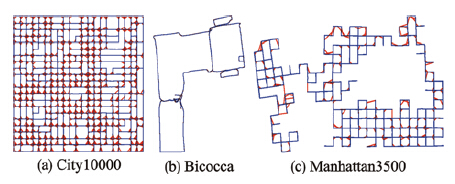 |
| 图 6 ASC算法结果节点(蓝)和边(红)Fig. 6 Nodes (red) and edges (blue) of the ASC result |
对比图 3与图 6可发现,City10000节点拓扑正确性较高,而Bicocca和Manhattan3500则发生一定程度的拓扑倾斜现象. 这是由于原始数据中部分节点误差较大,且缺少足够有效的闭环约束来纠正里程计误差. 如图 4中Bicocca数据集,可发现其存在“绑架”现象,机器人轨迹发生跳变. 而对于Manhattan3500数据集,观察图 7发现,原始数据集中只有A区、B区和C区存在有效的闭环约束,它们之间的连接部分D区却没有足够有效的闭环约束. 从算法的结果来看,正是D区中的节点偏差导致节点拓扑产生倾斜.
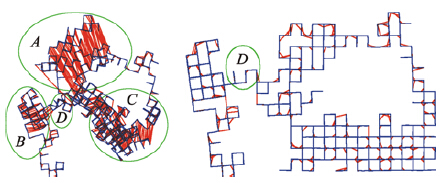 |
| 图 7 Manhattan原始数据集与优化数据集图结构Fig. 7 The graph structure of the raw Manhattan dataset and the optimizated dataset |
从表 2可见,在不同类型、 不同数量的闭环异常下,ASC算法的收敛时间明显优于SC算法. 对于初始节点位姿精度不同的两种Manhattan3500数据集,相比Olson版本,g2o版本收敛时间较短,可见对于Graph SLAM来说,其前端的精确度是必须考虑的因素. 两种算法在处理随机性的异常闭环(R,RG)时,收敛时间随异常闭环数量上升都有很大增长. 这是由于随机性错误闭环对整个图结构产生较大影响,使节点位姿几乎完全偏离真实位姿. 因此需要SC算法和ASC算法通过较多次数的迭代优化过程才能达到收敛. 而局部性错误闭环只对局部区域的节点位姿产生负面影响,虽然使节点偏离真实情况,但仍处在其附近区域,相对来说需要的迭代次数较少. 但总体说,无论对于随机性错误闭环还是局部性错误闭环,ASC算法收敛更快. 而对于Bicocca数据集,在标准参数设置下(w=1),SC算法不能得到有效的图结构.
由于一个节点的位姿误差会对接下来的所有节点的位姿都产生影响,采用RMSE(root mean square error)值在评价节点图时不能有效评价其局部一致性,因此本文使用RPE(relative pose error)值衡量算法结果与真实数据的差距. 其计算方法如下:
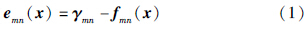
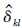 为真实节点
为真实节点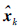 与
与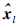 之间的相对转移量.
之间的相对转移量. 由于ASC和SC算法结果类似(除Bicocca数据集),这里只给出在不同类型、 不同数量的异常闭环下,ASC算法的RPE值,见图 8. 对于City10000,Manhattan3500和Bicocca数据集,ASC算法都可以较好地得到比较精确的图结构. 通过实验发现,对于随机性的异常闭环(R,RG),SC和ASC算法的RPE值随异常闭环数量上升都有一定增长,但相比常规Graph SLAM算法依然能够保持节点拓扑的一致性. 而在对局部性闭环(L,LG)的实验中,SC和ASC算法都可以达到非常好的效果,RPE值在不同异常闭环数量下都能够保持相对稳定(10-4 m~10-5 m),可见算法对局部性异常闭环的影响有很好的消除作用,体现了算法的有效性.
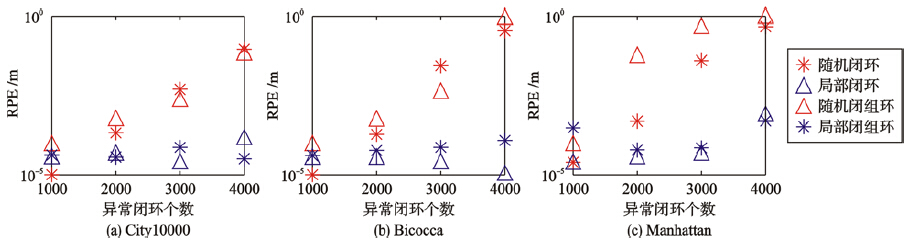 |
| 图 8 ASC算法的RPE值Fig. 8 RPE of the ASC algorithm |
本文在SC算法的基础上,对代价函数中的参量进行定性和定量分析,利用最新迭代信息更新这些参量,动态调整闭环对节点位姿的影响,将错误闭环的影响力大大降低,从而加快算法收敛速度,且对不同的数据集有良好的适应性. 另外,实验表明ASC算法在处理局部性异常闭环时具有较大的优越性,对随机性异常闭环的数据集在收敛速度上有一定的优势. 而Bicocca数据集的对比实验表明,ASC算法更具鲁棒性,适应性更强. 下一步将继续研究在随机性异常闭环条件下如何进一步提高算法实效性和精确度,从而加强算法的有效性.
| [1] | Bailey T, Durrant-Whyte H. Simultaneous localization and mapping (SLAM): Part I[J]. IEEE Robotics & Automation Magazine, 2006, 13(2): 99-108. |
| [2] | Smith R C, Cheeseman P. On the representation and estimation of spatial uncertainty[J]. The International Journal of Robotics Research, 1986, 5(4): 56-68. |
| [3] | 祝继华, 郑南宁, 袁泽剑, 等. 基于中心差分粒子滤波的SLAM算法[J]. 自动化学报, 2010, 36(2): 249-257. Zhu J H, Zheng N N, Yuan Z J, et al. A SLAM algorithm based on central difference particle filter[J]. Acta Automatic Sinica, 2010, 36(2): 249-257. |
| [4] | Huang S, Dissanayake G. Convergence and consistency analysis for extended Kalman filter based SLAM[J]. IEEE Transactions on Robotics, 2007, 23(5): 1036-1049. |
| [5] | Lu F, Milios E. Globally consistent range scan alignment for environment mapping[J]. Autonomous Robots, 1997, 4(4): 333-349. |
| [6] | Frese U, Schroder L. Closing a million-landmarks loop[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2006: 5032-5039. |
| [7] | Grisetti G, Stachniss C, Burgard W. Nonlinear constraint network optimization for efficient map learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(3): 428-439. |
| [8] | Grisetti G, Kummerle R, Stachniss C, et al. Hierarchical optimization on manifolds for online 2D and 3D mapping[C]//2010 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2010: 273-278. |
| [9] | Kummerle R, Grisetti G, Strasdat H, et al. g2o: A general framework for graph optimization[C]//2011 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2011: 3607-3613. |
| [10] | Tipaldi G D, Braun M, Arras K O. FLIRT: Interest regions for 2D range data with applications to robot navigation[C]//Experimental Robotics. Berlin, Germany: Springer, 2014: 695-710. |
| [11] | Olson E. Recognizing places using spectrally clustered local matches[J]. Robotics and Autonomous Systems, 2009, 57(12): 1157-1172. |
| [12] | Cummins M, Newman P. FAB-MAP: Probabilistic localization and mapping in the space of appearance[J]. The International Journal of Robotics Research, 2008, 27(6): 647-665. |
| [13] | Latif Y, Cadena C, Neira J. Robust loop closing over time for pose graph SLAM[J]. The International Journal of Robotics Research, 2013, 32(14): 1611-1626. |
| [14] | Olson E, Agarwal P. Inference on networks of mixtures for robust robot mapping[J]. The International Journal of Robotics Research, 2013, 32(7): 826-840. |
| [15] | Sünderhauf N, Protzel P. Switchable constraints for robust pose graph slam[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2012: 1879-1884. |
| [16] | Olson E, Leonard J, Teller S. Fast iterative alignment of pose graphs with poor initial estimates[C]//2006 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2006: 2262-2269. |
| [17] | Kaess M, Ranganathan A, Dellaert F. iSAM: Fast incremental smoothing and mapping with efficient data association[C]//2007 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2007: 1670-1677. |
| [18] | Sünderhauf N. Vertigo: Versatile extensions for robust inference using graphical models[DB/OL]. (2013-01-08)[2014-04-12]. http://openslam.org/vertigo.html. |



