2. 中石化天然气分公司, 北京 100000;
3. 中国石油北京销售公司, 北京 100000
2. Sinopec Natural Gas Company, Beijing 100000, China;
3. China Petroleum Marketing Company, Beijing 100000, China
1 引言
天然气管网的运行优化就是在管网系统结构和外部条件已经确定的情况下,根据气源供气和用户用气需求条件变化,对管网系统的运行参数,即各节点的压力、 流量,进行优化,在满足气源条件和用户需求的前提下,降低运行费用,达到经济、 安全、 平稳输气的目的[1, 2, 3].
动态规划方法是管网运行优化研究中常用的方法,它将管网运行优化问题看成一个多阶段的优化过程,利用各阶段之间的递推关系,逐个求解并得到整个问题的最优解.相比其它方法,它更加简单有效,理论上能保证得到最优解,且一般求解效率较高[4, 5, 6, 7];但由于“维数灾难”和“无后效性”问题,动态规划方法在求解动态运行优化问题时效率较低,表现为求解时间过长或难以求解,因此有必要进行动态规划方法在管网动态运行优化中的应用研究. 为此,在分析管网动态运行优化模型的基础上,提出“时间层独立”假设,并进行了相关验证,然后基于该假设将多时间层的优化问题转变成多个独立时间层优化问题,从而有效避免了“维数灾难”和“无后效性”问题,以提高动态规划方法对管网动态运行优化问题的求解能力和效率.
2 管网动态运行优化模型天然气管网系统动态运行优化模型可分为目标函数、 约束条件和决策变量3个部分,且各部分均为时间的函数[8]. 此外,动态运行优化模型应当能够较为准确地描述天然气在管网系统中流动的实时状态. 文中采用如下数学模型:
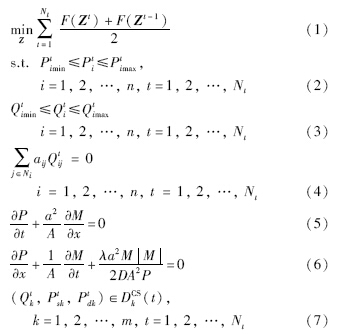
优化模型(1)~(7)中含有大量的非线性等式约束,由于其各节点的流量为时间的函数,模型求解具有一定难度. 为便于使用动态规划方法进行求解,将其描述成如下形式:
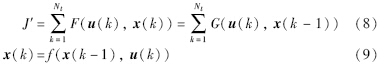
动态规划问题的维数即各阶段状态变量的维数.当状态变量的维数增加时,动态规划问题的计算量和计算时间会呈指数倍增长,限制了利用动态规划研究问题和解决问题的能力,这种情形被称之为“维数灾难”[15, 16].
利用动态规划方法对管网动态运行优化模型进行求解时,k阶段的状态变量可以根据k阶段决策变量和前一阶段的状态进行计算. k(k
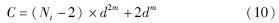
在动态规划方法的使用中要求某个阶段上的状态,应当只受该阶段相邻的前一个阶段状态的影响,而与以前各阶段状态无关,即“无后效性”[17].
根据“无后效性”要求,在应用动态规划方法寻优的过程中,对于任一阶段的决策点,其状态应该与到达该点以前的经历无关[18, 19]. 如图 1所示,A决策点对应的状态(各压气站的流量和入站压力)应当与到达该节点的路径无关,而在进行管网运行动态水力实际计算时,从路径1或路径2等不同路径(阶段1采用不同的控制策略)到达A节点,所引起的管网状态可能并不一致,不满足“无后效性”原则.
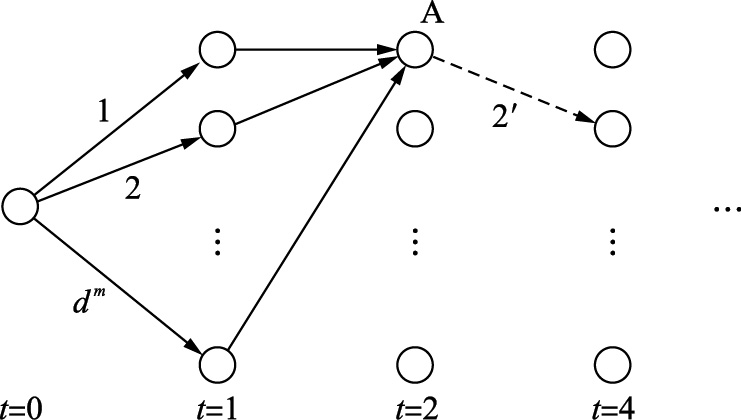 |
| 图 1 动态规划无后效性示意图Fig. 1 Ineffective schematic of dynamic programming |
如上所述,A决策点的状态可能与到达节点的路径有关系,因此该节点所对应的状态可能不止一种.为了保证找到最优解,应当记录A节点的所有可能状态,并在下一阶段的寻优时,一一考虑这些状态. 这无疑使计算量再次变大,严格意义上来讲,k阶段的状态数从原先的dm增大到dk×m. 若只记录到达A节点的最优路径所对应的状态,而丢弃其它状态,则会使寻优过程不严谨,可能无法得到最优解. 因为,这些丢失的路径虽然不是到达A节点的最优路径,但可能是到达终点阶段最优路径中的一部分.
4 模型求解由于“维数灾难”和“无后效性”问题的存在,从求解效率和可靠性的角度来讲,不能直接使用动态规划方法对管网动态运行的优化模型进行求解,为此,提出了“时间层独立”假设,下面首先对该假设进行验证,然后再给出具体的求解方法.
4.1 “时间层独立”假设“时间层独立”假设即管网在单个时间层(2 h)内可以过渡到任意可行的稳定状态(除分输站外). 为了验证“时间层独立”假设的可行性,采用TGNET软件对天然气管道动态运行特性进行仿真实验. 观察在一定初始条件和入口、 出口流量边界条件下,管道在给定的时间(2 h)内,能否达到新的稳定状态.
图 2为利用TGNET软件建立的单管道模型. 该模型中,管段长度L=50 km,内径D=0.6 m. 初始状态为稳定状态,入口压力Pin=5 MPa,出口压力Pout=4.772 7 MPa,流量Q=200 kN·m3/h.
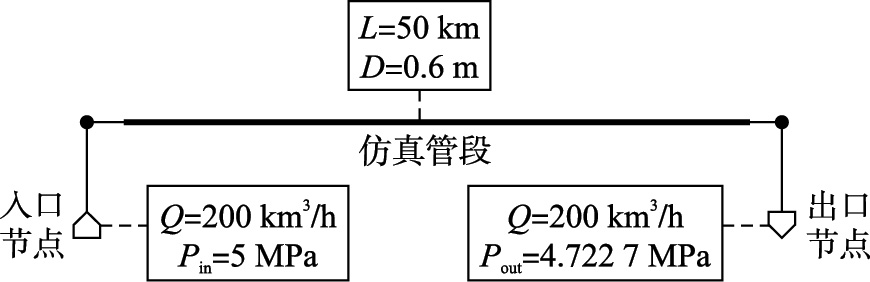 |
| 图 2 天然气管道动态运行仿真模型Fig. 2 The dynamic simulation model of natural gas pipe |
边界流量条件如图 3所示,①、②、③为3种不同的流量边界条件,起点时刻流量为200 kN·m3/h,曲线①在0.2 h后达到300 kN·m3/h,曲线②、 ③皆在0.5 h后达到300 kN·m3/h,曲线②为直线形式,曲线③为抛物线形式.
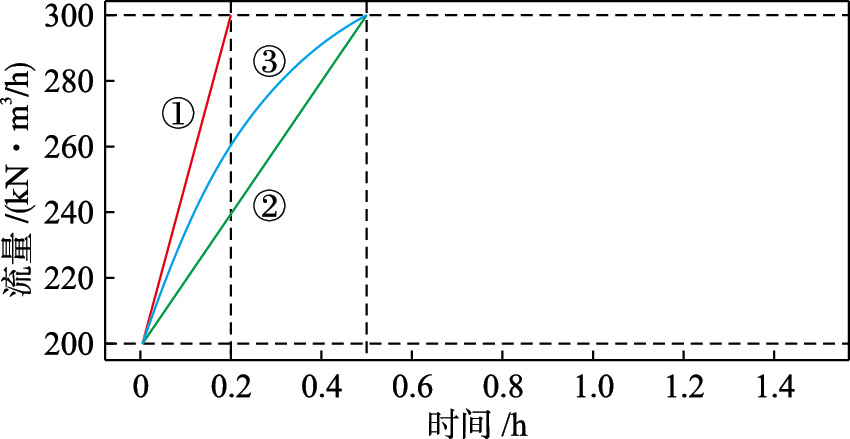 |
| 图 3 流量边界曲线Fig. 3 The flow boundary curves |
分别以曲线①、 ②、 ③作为不同的入口、 出口边界条件进行管道的动态运行仿真,其仿真结果如表 1所示.
|
仿真 实验 | 入/出口 边界条件 | 稳定时间 /h | 稳定时刻 Pin/MPa | 稳定时刻 Pout/MPa |
| 1 | ①、 ① | 0.9 | 5.138 1 | 4.626 1 |
| 2 | ②、 ② | 1.1 | 5.138 1 | 4.626 1 |
| 3 | ③、 ③ | 1.1 | 5.138 1 | 4.626 1 |
| 4 | ①、 ② | 1.1 | 5.218 4 | 4.716 0 |
| 5 | ①、 ③ | 1.1 | 5.180 7 | 4.673 9 |
| 6 | ②、 ① | 1.1 | 5.057 9 | 4.535 9 |
| 7 | ②、 ③ | 1.1 | 5.100 6 | 4.584 0 |
| 8 | ③、 ① | 1.1 | 5.095 5 | 4.578 3 |
| 9 | ③、 ② | 1.1 | 5.175 7 | 4.668 3 |
根据上述仿真实验结果可以看出,对于单个管道,在给定的入口、出口边界条件下,管段在2h内可以达到新的稳定状态(管道中各节点的压力和流量不随时间变化),且新稳态下压力分布于边界条件存在一定的数值关系. 为确定这种数值关系,进行如下推导过程.
Step 1: 对式(5),令时间t为定值,假设管道长度为L,对x进行0~L的积分:
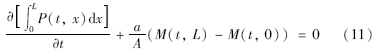
Step 2: 设te时刻及以后,管道达到目标稳态,即期望管道所达到的稳定状态和压力分布,对上式进行从t0~te的积分:
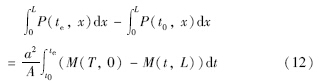
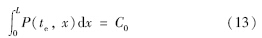
Step3: 令t=te,对(6)式中x进行0~L的积分:
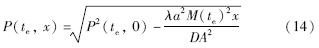
Step4: 将式(14)代入式(13)中,可解得:
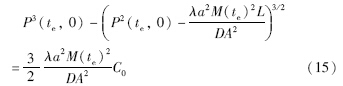
Step5: 将(15)式进一步简化成如下形式:
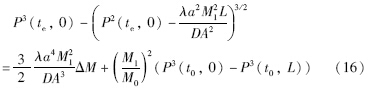
式(16)描述了在给定初始状态下,管道目标稳态与管道容量变化值的关系式,如果ΔM与P(te,0)存在唯一对应关系,则证明管容变化与目标稳态的唯一对应关系.
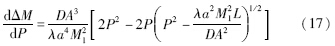
式(17)为ΔM与目标状态入口节点压力P的一阶导数,等式右边第二项为管道目标状态出口节点压力,显然有:
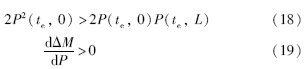
式(19)表示ΔM为目标压力P的单调函数,在给定初始状态下,管道目标稳态与管道容量变化存在唯一对应性. 即当管道压力和流量达到指定的新稳定状态时,管道中所包含的天然气的总质量相对于初始时刻的变化量是唯一确定的,不同的稳定状态对应不同的管容变化量.
根据上述仿真实验和相关推导,发现管网中各管段的管容变化与目标稳态之间存在唯一对应关系,只要管容变化达到目标值且边界流量满足稳定条件,则除分输站外,管网可以在单个时间层(2 h)内过渡到一定范围内任意稳定状态.
4.2 动态规划求解方法设计基于“时间层独立”假设,优化模型(8)、(9)可重新表述如下:

由式(20)可以看出,经过“时间层独立”处理,每个阶段管网的状态都为稳定状态,不依赖于前一阶段,仅由本阶段的决策变量来确定,因此可以将多个时间层的动态优化问题转变成若干个独立的单时间层优化问题. 这样不仅避免了“维数灾难”问题,同时满足了动态规划方法对“无后效性”的要求,可提高优化求解的效率和准确性.
经过上述分析,动态规划方法在管网动态运行优化问题求解中的具体步骤为:
Step 1: 输入管网系统结构信息. 确定系统中气源节点、 分输节点、 压气站数量和管网结构.
Setp 2: 输入管网系统初始状态和边界条件. 其中,初始状态表示动态运行优化初始时刻管网的稳定状态,主要包括各节点流量、 压力值,各压气站入站压力、 流量、 出站压力值. 边界条件为气源节点和分输节点的流量随时间变化的曲线.
Step 3: 确定优化时间层数和时间步长. 一般情况下,进行24 h动态运行优化,优化时间层数和时间步长成反比关系,优化时间层数越大,时间步长越小. 理论上来讲,优化时间层数越大,优化效果越好,相应的计算量也越大. 需要注意的是,本文主要基于“时间层独立”假设进行动态运行优化,因此这里建议时间步长不要小于1 h.
Step 4: 令N=1,准备进入第N时间层的优化.
Step 5: 计算第N时间层管网稳态流量.根据N时间层气源节点的流量和管网结构计算稳态时各管段各压气站的流量.这里分输站和分输管段一般不处于稳定状态,此时由分输管段管容的变化或相关储气设备进行流量调整,以满足分输节点流量的要求.
Step 6: 计算第N时间层各分输站出站压力.根据式(15)和式(16)建立分输管段动态水力计算的方程组,并进行若干次迭代计算,得到N时间层终点时刻,分输管段入口压力,即分输站的出站压力.
Step 7: 进行第N时间层的优化求解. 采用自适应动态规划方法[11]对除分输站和分输管段外的管网系统进行优化求解.
Step 8: 判断动态运行优化是否结束. 若时间层N为最后一个时间层,则动态运行优化结束,进入下一步,否则,令N=N+1,转入Step 5.
Step 9: 得到管网系统动态运行的最优决策u*,即各时间层各压气站的最优出站压力值.
5 仿真分析基于前面所述的时间层独立化处理方法,利用自适应动态规划方法进行天然气管网动态运行优化求解,并用Matlab进行方法仿真和分析.
建立如图 4所示的管网简化模型为经过简化的模型[20],其中包含6个压气站、 9个管段、 15个节点、1个气源节点和2个分输节点,各部分的约束条件如表 2和表 3所示.
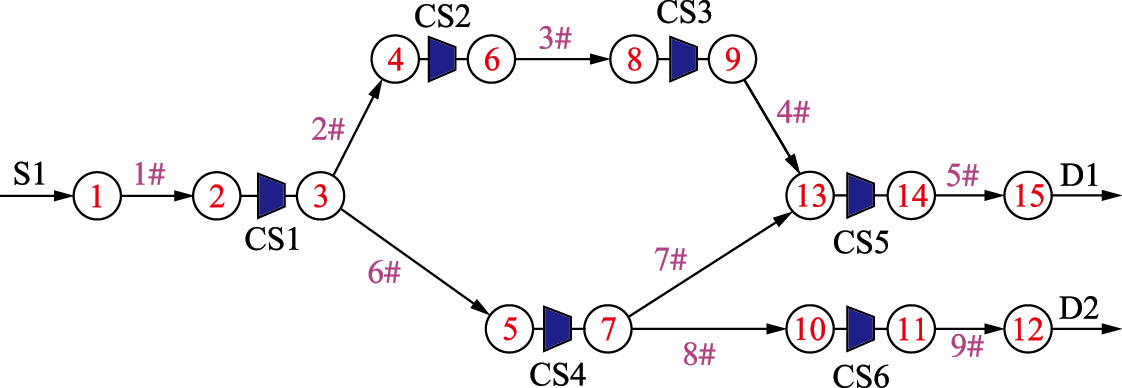 |
| 图 4 天然气管网模型Fig. 4 Natural gas network model |
| 压气站 | 入站压力 限制/MPa | 出站压力 限制/MPa | 流量限制 /(kN·m3/h) | 压比限制 |
| 1 | 3.0~5.5 | 3.0~5.5 | 20~300 | 1~1.5 |
| 2 | 3.0~5.5 | 3.0~5.5 | 20~300 | 1~1.4 |
| 3 | 3.0~5.5 | 3.0~5.5 | 20~300 | 1~1.5 |
| 4 | 3.0~5.5 | 3.0~5.5 | 20~300 | 1~1.5 |
| 5 | 3.0~5.5 | 3.0~5.5 | 20~300 | 1~1.6 |
| 6 | 3.0~5.5 | 3.0~5.5 | 20~300 | 1~1.7 |
| 管段 | 内径/m | 长度/m | 平均温度/K | 压力限制/MPa |
| 1 | 0.8 | 50 000 | 300 | 2.5~5.0 |
| 2 | 0.7 | 40 000 | 300 | 2.5~5.0 |
| 3 | 0.6 | 55 000 | 300 | 2.5~5.0 |
| 4 | 0.8 | 45 000 | 300 | 2.5~5.0 |
| 5 | 0.8 | 40 000 | 300 | 2.5~5.0 |
| 6 | 0.8 | 40 000 | 300 | 2.5~5.0 |
| 7 | 0.7 | 40 000 | 300 | 2.5~5.0 |
| 8 | 0.7 | 45 000 | 300 | 2.5~5.0 |
| 9 | 0.7 | 40 000 | 300 | 2.5~5.0 |
设气源节点1的流量保持不变,分输节点12、15的用气量变化曲线如图 5所示. 将24 h划分为12个时间层,以6时刻为动态运行优化的初始时刻t0,每个时间层步长为2 h.
 |
| 图 5 分输节点日用气量曲线Fig. 5 Daily gas consumption curve of deliver nodes |
管网的初始状态如表 4所示,由于气源节点供气量保持不变,因此各时间层管网稳定状态下各压气站流量分配与初始状态保持一致. 分输管段动态水力计算的子时间步长为10 min,剖分段的长度为20 km,决策量离散点为3.
| 压气站 | 入站压力 /MPa | 出站压力 /MPa | 流量 /(kN·m3/h) | 功率 /MW |
| 1 | 3.898 0 | 4.035 1 | 600 | 0.496 1 |
| 2 | 3.920 0 | 4.115 9 | 200 | 0.233 4 |
| 3 | 3.751 6 | 3.751 6 | 200 | 0 |
| 4 | 3.805 9 | 3.805 9 | 400 | 0 |
| 5 | 3.683 6 | 3.748 0 | 400 | 0.165 6 |
| 6 | 3.668 0 | 3.668 0 | 200 | 0 |
对于图 4所示的模型,若直接采用动态规划方法进行求解,由式(10)可得到其计算量C=5 315 868.其中,每次计算都需要进行如式(9)所示的管网动态运行水力计算.这种水力计算要求首先对整个管网的管段划分成若干个剖分段,将时间层划分成若干个子时间层,然后联立方程组,进行多次迭代求解,需要大量时间,假设每次水力计算耗时为0.1 s,则一次动态规划方法的时间为531 586.8 s>24 h.
采用时间层独立化处理并利用自适应动态规划方法依次对各时间层进行优化求解. 若每个时间层动态规划次数为设定最大求解次数50,则其计算量C2=50×(5×32+3)×(12-1)=26 400,与前面相比,有C2C,且每次计算过程中不需要进行动态水力计算. 程序运行时间约7.90 s,每个时间层动态规划寻优次数为35~50次,较大程度地提高了求解效率. 图 6为各时间层管网系统的总功率曲线,图 7和图 8为各时间层各压气站的动态运行优化结果.
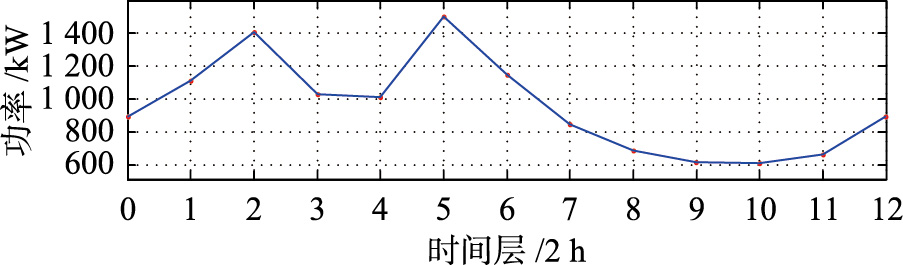 |
| 图 6 各时间层管网总功率Fig. 6 Networks′ total power of per time layer |
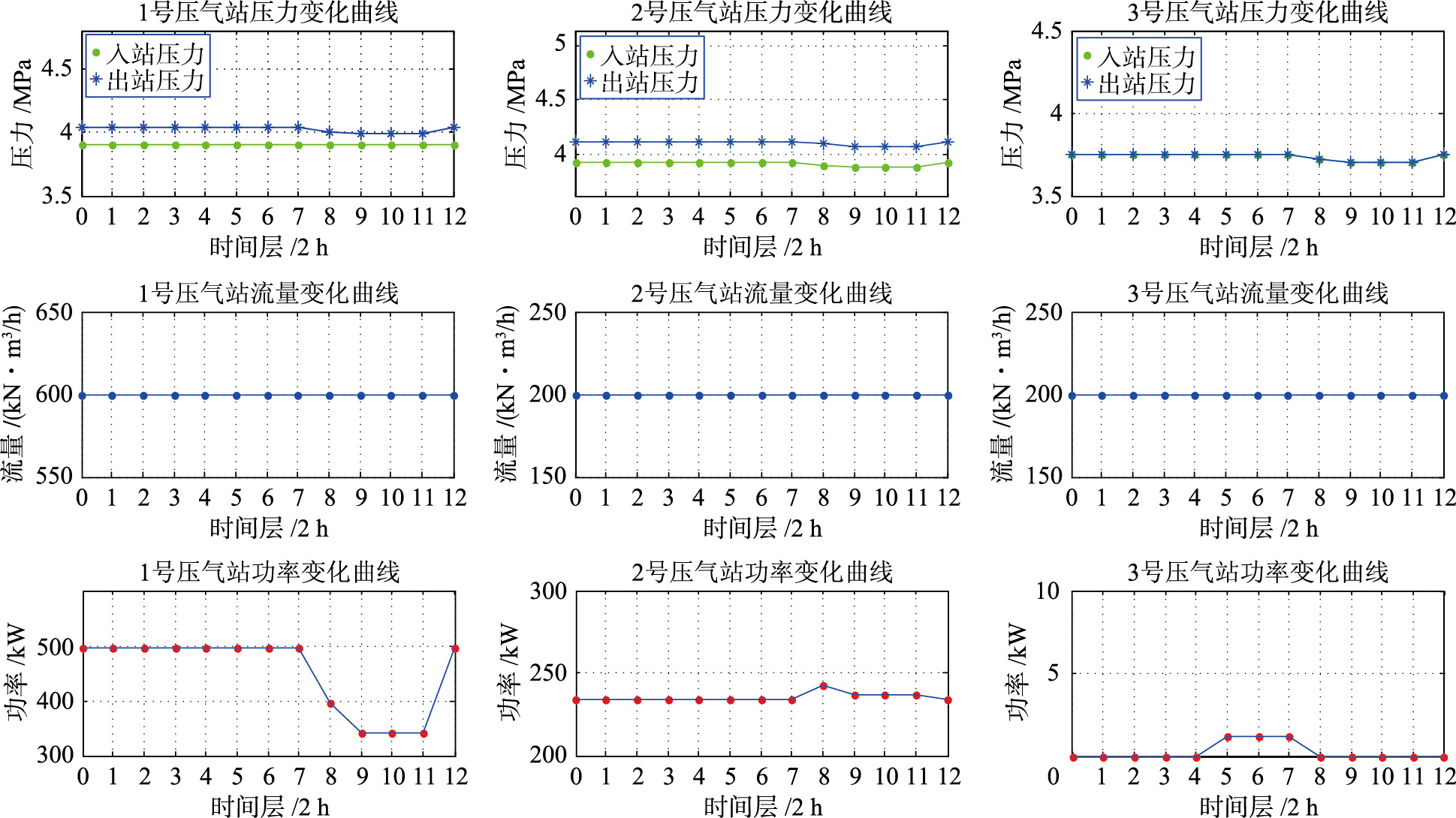 |
| 图 7 1~3号压气站各时间层寻优结果Fig. 7 Per time layer optimization results of compressor station 1~3 |
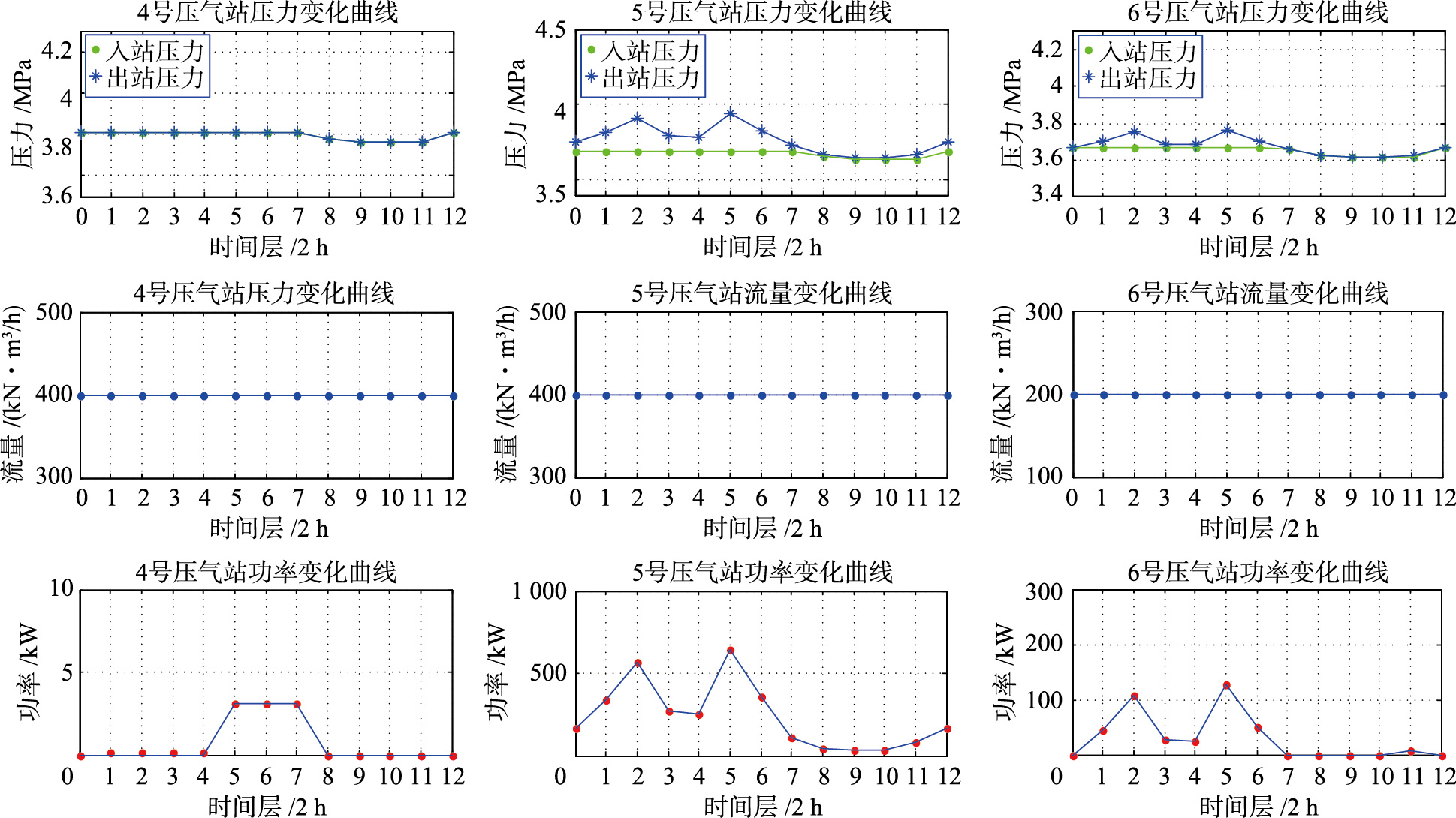 |
| 图 8 4~6号压气站各时间层寻优结果Fig. 8 Per time layer optimization results of compressor station 4~6 |
从图 6可以看出,优化后管网的能耗随用气量的变化而变化. 用气量增加,能耗增加; 用气量减少,管网能耗也相应地减少. 终点时刻与初始时刻管网状态保持一致. 显然动态运行优化可以根据实际气源供气量和用户用气量情况获得更好的运行优化效果,有利于降低管网运行成本. 需要注意的是,如图 9中,分输节点的压力在某些时刻并没有满足合同压力,可以考虑提高初始条件中分输站5和6的出站压力或者提高相应时间层的分输气量.
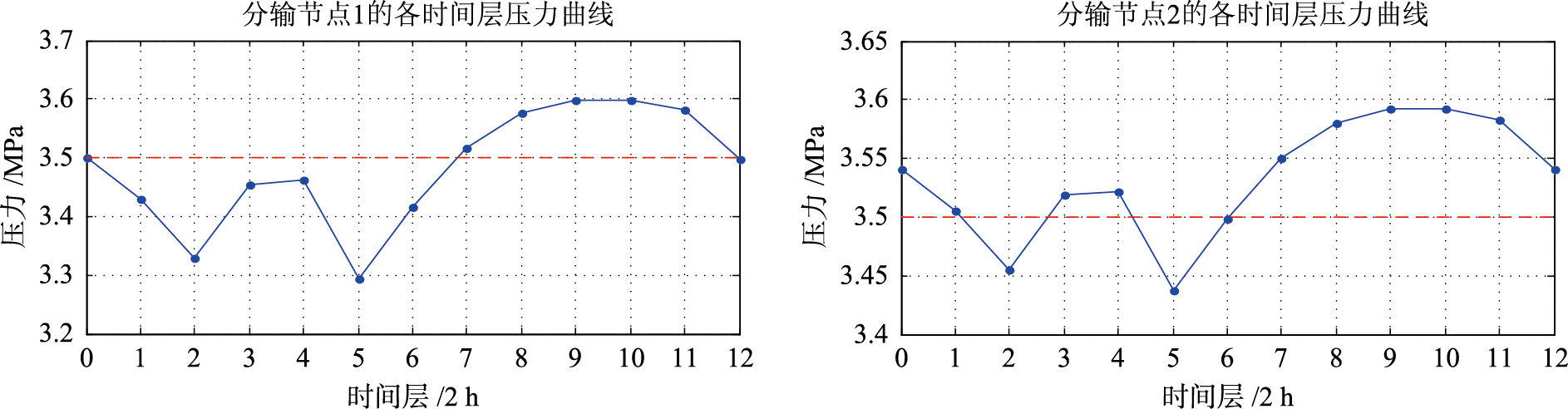 |
| 图 9 各时间层分输节点压力Fig. 9 Deliver node pressure of per time layer |
针对动态规划方法在求解管网动态运行优化问题时存在的“维数灾难”和“无后效性”问题,提出了“时间层独立”假设并对其进行了验证,基于该假设将多时间层优化问题转变成若干个独立的单时间层优化问题,以便于利用动态规划方法进行求解.仿真结果表示:本文提出的时间层独立化处理方法能有效地避免上述问题,较大程度地提高动态规划方法对管网动态运行优化问题的求解效率.
| [1] | 贺三, 邹永莉, 王欣. 天然气管道的运行优化[J]. 油气储运, 2009, 28(6): 1-7. He S, Zou Y L, Wang X. Optimization of natural gas pipeline networks[J]. Oil Gas Storage and Transportation, 2009, 28(6): 1-7. |
| [2] | 艾慕阳, 蒋毅, 宋飞, 等. 大型天然气管网运行方案多目标决策优化计算[J]. 油气储运, 2011, 30(10): 739-742. Ai M Y, Jiang Y, Song F, et al. Multi-objective decisions optimization of larger natural gas networks operation scheme[J]. Oil Gas Storage and Transportation, 2011, 30(10): 739-742. |
| [3] | Chebouba A, Yalaoui F. Optimization of natural gas pipeline transportation using ant colony optimization[J]. Computer & Operations Research, 2009, 36(6): 1916-1923. |
| [4] | 李博, 何淼, 李江飞, 等. 求解天然气管网运行优化问题的TDDP算法[J]. 石油工程建设, 2014, 40(2): 6-10. Li B, He M, Li J F, et al. A TDDP algorithm for optimizing natural gas pipeline network operation[J]. Petroleum Engineering Construction, 2014, 40(2): 6-10. |
| [5] | Borraz-Sanchez C, Rios-Mercado R Z. A non-sequential dynamic programming approach for natural gas network optimization[J]. WSEAS Transactions on Systems, 2004, 3(4): 1384-1389. |
| [6] | 张化光, 张欣, 罗艳红, 等. 自适应动态规划综述[J]. 自动化学报, 2013, 39(4): 303-311. Zhang H G, Zhang X, Luo Y H, et al. An overview of research on adaptive dynamic programming[J]. Acta Automatica Sinica, 2013, 39(4): 303-311. |
| [7] | Lall H S, Percell P B. A dynamic programming based gas pipeline optimizer[M]//Analysis and Optimization of Systems. Berlin, Germany: Springer, 1990: 123-132. |
| [8] | Borraz-Sanchez C. Optimization methods for pipeline transportation of natural gas[D]. Norway: University of Bergen, 2010: 56-57. |
| [9] | Marc C S. On PDE solution in transient optimization of gas networks[J]. Journal of Computational and Applied Mathematics, 2007(203): 345-361. |
| [10] | 李长俊. 天然气管道输送[M]. 北京: 石油工业出版社, 2008: 61-62. Li C J. Transportation of natural gas pipeline[M]. Beijing: Petroleum Industry Press, 2008: 61-62. |
| [11] | Pia D, Bjorn G, Alexander M, et al. Combination of nonlinear and linear optimization of transient gas network[J]. Informs Journal on Computing, 2011, 23(4): 605-617. |
| [12] | 杨毅. 天然气管道运行优化模型及其寻优方法研究[D]. 成都: 西南石油学院, 2006: 62-67. Yang Y. Optimization model and solution researches of natural gas transportation networks[D]. Chengdu: Southwest Petroleum University, 2006: 62-67. |
| [13] | Wu S, Rios-Mercado R Z, Boyd E A, et al. Model relaxations for the fuel cost minimization of steady-state gas pipeline networks[J]. Mathematical and Computer Modeling, 2000, 31(2): 197-220. |
| [14] | 刘武, 张鹏, 刘稀, 等. 天然气管网优化调度方法研究[J]. 西南石油大学学报, 2009, 31(3): 146-148. Liu W, Zhang P, Liu X, et al. Algorithm research of natural gas transportation networks optimization[J]. Journal of Southwest Petroleum University, 2009, 31(3): 146-148. |
| [15] | Lei Y, Jennie S, Konstantinos S, et al. Performance evaluation of direct heuristic dynamic programming using control-theoretic measures[J]. Journal of Intelligent Robotic Systems, 2009, 55(2): 177-201. |
| [16] | 孙健, 刘锋, 郭文涛, 等. 一种改进的近似动态规划方法及其在SVC的应用[J]. 电机与控制学报, 2011, 15(5): 95-102. Sun J, Liu F, Guo W T, et al. An improved approximate dynamic programming and its application in SVC control[J]. Electric Machines and Control, 2011, 15(5): 95-102. |
| [17] | 厉洋峰. 动态规划及其在数学模型中的应用[J]. 中国新技术产品, 2009, 15(16): 244-245. Li Y F. Dynamic programming and its application in mathematic models[J]. China New Technologies and Products, 2009, 15(16): 244-245. |
| [18] | 胡寿松, 王执铨, 胡维礼. 最优控制理论与系统[M]. 北京: 科学出版社, 2005: 130-157. Hu S S, Wang Z Q, Hu W L. Optimal control theory and system[M]. Beijing: Science Press, 2005: 130-157. |
| [19] | Borraz-Sanchez C, Haugland D. Minimizing fuel cost in gas transmission networks by dynamic programming and adaptive discretization[J]. Computers & Industrial Engineering, 2011, 61(2): 364-372. |



