2. 重庆大学自动化学院, 重庆 400044
2. College of Automation, Chongqing University, Chongqing 400044, China
1 引言
众所周知，不稳定零动态限制了控制系统可达到的控制性能.当过程或对象存在不稳定零动态时，很难构建一些控制系统，如逆系统、 鲁棒控制器、 模型匹配系统和模型参考自适应控制器等[1, 2, 3]. 当采用零阶保持器(zero-order hold，ZOH)对一个连续时间系统进行离散化时，稳定的极点被映射到单位圆内，从而保证了系统的稳定性.然而相对于零动态，连续时间系统与其相应的离散时间系统之间却不存在如此简单的对应关系[4, 5, 6]. 因此关于线性离散零动态特性的研究引起了研究者的广泛观注[7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18].
关于离散时间系统零动态的奠基性研究是由著名的瑞典学者ÅstrÖm等[4]于1984年提出的. 离散时间系统的零动态分为两类[8]： 一类是真性零动态(intrinsic zero dynamics)，它与原连续时间系统的零动态相对应，是在采样过程中从连续时间系统中保留下来的；另一类是采样零动态(sampling zero dynamics)，它是在采样过程中新产生出来的，这也导致了离散时间系统零动态的数量和连续时间系统零动态的个数不同，同时也是采样过程影响离散系统零动态稳定性的重要原因. 在ZOH和快速采样条件下，相对阶(relative degree)为1的连续时间系统的相应离散时间模型零动态均为真性零动态[10]，此时只要连续时间系统零动态是稳定的，则相应离散时间系统零动态也是稳定的； 当连续时间系统的相对阶大于或等于3时，即使原连续时间系统的零动态是最小相位的，至少有一个采样零动态呈现非最小相位特性[4]； 然而，当连续时间系统的相对阶为2时，相应的离散时间系统的采样零动态仅仅位于单位圆上，其稳定性的程度是无法判定的.另一方面，上述研究也表明离散时间系统的采样零动态和原连续时间系统的相对阶有密切的联系，但遗憾的是目前的研究成果并未给出采样零动态的具体渐近特征和稳定准则，只是从理论体系上说明离散化采样零动态收敛到特定多项式的特征根.因此，从采样零动态稳定性的观点出发，采样零动态能否保持稳定就成为一个值得关注的科学问题.
针对上述情况中采样零动态在单位圆上能否保持稳定这一科学问题，本文将重点关注相对阶为2的连续时间系统的相应离散时间模型采样零动态的渐近性质. 通过采用标准型(normal formal)和泰勒幂级数展开式导出离散系统零动态关于采样周期T的4阶近似表达式. 并指出相对阶为2时，相应离散时间系统的采样零动态在快速采样和零阶保持器条件下从单位圆内部趋近于-1. 最后给出保持采样零动态稳定的条件，该条件可用于一类非线性离散系统采样零动态的判定.
2 理论基础考虑相对阶为2的连续时间系统传递函数为
当采用零阶保持器进行离散化时，有u·=ü=…=0，从而根据标准型(2)可得到变量y和变量η的各阶导数. 进一步，将变量y的1到6阶导数和η的1到5阶导数代入下式：
通过第2节的分析可知，连续时间系统(1)的相应离散时间系统零动态渐近特性可由下面的定理1来描述.
定理1 当T«1时，相对阶为2的连续时间系统(1)的相应离散时间系统零动态由式(8)决定：
证明 相对阶为2的连续时间系统(1)的相应离散时间系统零动态可通过将yk=yk+1=0代入式(5)～(7)导出. 首先，将(5)～(7)表示成矩阵形式：
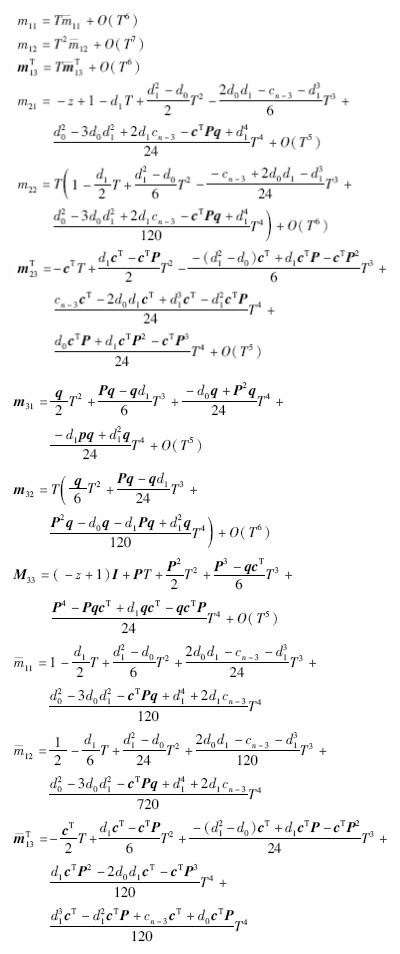
因此，相对阶为2的连续时间系统(1)的相应离散时间系统零动态是方程
由于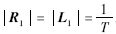
，则：
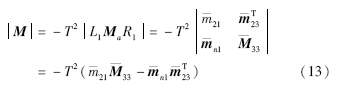
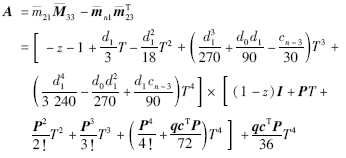
令A=B+E，则有：
通过简单的计算，可以有|E|=O(T5). 因此，式(8)的根就是相对阶为2的连续时间系统(1)的相应离散时间系统零动态的近似值.
注1 离散时间系统零动态由方程(8)决定，其中采样零动态和真性零动态的近似值分别为
进一步，由前面的定理1可导出下面的推论：
推论1 假设连续时间系统(1)的相对阶数为2，如果d1=an-1-bn-3>0(<0)，则采样零动态在T«1时是稳定(不稳定)的.
推论2 假设连续时间系统(1)的相对阶数为2，并且零动态的和等于极点的和，即d1=an-1-bn-3=0，则相应的离散时间系统采样零动态可以表示为
进一步，如果有：
注2 当相对阶为2的连续时间系统有d1=0时，则cn-3与-cTmA5mbm/K是等价的，其中(Am，bm，cm)表示为连续时间系统(1)的最小实现.
在本节的最后部分，可通过下面的分析说明推论1的结果能用于一类非线性系统采样零动态的稳定性判别. 考虑相对阶为2的非线性控制系统的标准形为
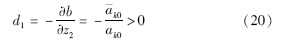
注3基于标准形来导出离散化零动态的渐近特征有更高的精确度，且采样零动态的稳定条件和渐近性有密切联系，有利于镇定控制器的设计. 4 仿真分析
本节首先通过两个例子来验证本文中采样零动态的稳定条件，然后通过两个经典例子来说明本文的主要结果怎样用于一类非线性控制系统采样零动态的稳定性判别. 考虑一个相对阶为2的连续时间系统，其极点的和等于零动态的和：
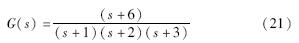
因此，系统(21)的相应离散时间系统零动态的近似值和精确值可由表 1来描述.
| T | 近似值 | 精确值 |
| 0.01 | -0.999 998 000，0.941 764 000 | -0.999 998 001，0.941 764 533 |
| 0.02 | -0.999 984 000，0.886 912 000 | -0.999 984 021，0.886 920 411 |
| 0.05 | -0.999 750 000，0.740 500 000 | -0.999 752 042，0.740 816 150 |
| 0.1 | -0.998 000 000，0.544 000 000 | -0.998 064 368，0.548 763 414 |
| 0.2 | -0.984 000 000，0.232 000 000 | -0.985 895 895，0.300 398 195 |
由仿真实例(21)知： 式(8)的特征根与系统离散化零动态的实际值接近，且在快速采样条件下(T→0)，其相应的采样零动态都可以保持稳定. 图 1和图 2分别表示在快速采样和ZOH条件下系统(21)相应的采样零动态和真性零动态.
 |
| 图 1 离散时间系统的采样零动态Fig. 1 Sampling zero dynamics of discrete-time system |
 |
| 图 2 离散时间系统的真性零动态Fig. 2 Intrinsic zero dynamics of discrete-time system |
考虑一个如图 3所示的电路平面图. 其中Ri(i=1，…，4)和Cj(j=1，…，3)分别表示电阻和电容，ei(t)和e0(t)分别表示输入和输出，同时其传递函数：
 |
| 图 3 电路系统Fig. 3 Circuit system plant |
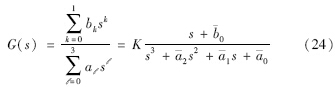
，明显可知该系统的相对阶是2. 当参数分别为R1=R2=1 kΩ，R3=13/70 kΩ，R4=1/10 kΩ，C1=C2=C3=1 μF，则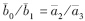
. 进一步，采样零动态可近似表示为
由式(25)可知，在快速采样条件下，采样零动态严格位于单位圆内.
在系统(24)中，采样零动态的近似值(25)和精确值分布如图 4所示，其中虚线和实线分别代表近似值和精确值. 从图 4可知，在快速采样条件下，图 3所示的电路系统的采样零动态的近似值和精确值接近，具有良好的仿真意义.
 |
| 图 4 电路系统采样零动态的分布Fig. 4 Sampling zero dynamics distribution of circuit system |
下面考虑2个经典的非线性模型，Van der Pol模型和Pendulum模型[19]：
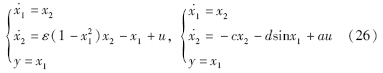
由文[21]可知，Van der Pol模型的采样零动态不稳定，而Pendulum模型则有稳定的采样零动态. 现由式(20)可判别知dv=-ε<0，dp=c>0，故本文的结论与文[21]的结果保持一致，即Van der Pol模型的采样零动态不稳定，而Pendulum模型的采样零动态稳定.
5 结论本文针对相对阶为2的连续时间系统，分析了在ZOH条件下相应的离散时间系统采样零动态的渐近性质，给出了采样零动态关于采样周期的4阶近似幂级数表达式. 并当T→0时的采样零动态的稳定条件.最后论文指出关于线性系统采样零动态的稳定条件也可用于一类非线性控制系统采样零动态稳定性的判别.此外，通过仿真例子可以得知本文的结果具有很好的精确性和有效性，本文的结果是前期研究成果的进一步扩展，将本文结果推广到多变量系统是需要进一步开展的工作.
| [1] | Åström K J, Wittenmark B. Computer controlled systems[M]. 3rd ed. New York, USA: Courier Dover Publications, 2011. |
| [2] | Åström K J, Wittenmark B. Adaptive Control[M]. 2nd ed. New York, USA: Courier Dover Publications, 2008. |
| [3] | Isidori A. The zero dynamics of a nonlinear system: From the origin to the latest progresses of a long successful story[J]. European Journal of Control, 2013, 19(5): 369-378. |
| [4] | Åström K J, Hagander P, Sternby J. Zeros of sampled systems[J]. Automatica, 1984, 20(1): 31-38. |
| [5] | 曾诚, 梁山, 李洪兵, 等. 离散时间系统零动态的研究现状和未来挑战[J]. 控制理论与应用, 2013, 30(10): 1213-1230. Zeng C, Liang S, Li H B, et al. Current development and future challenges for zero dynamics of discrete-time systems[J]. Control Theory & Applications, 2013, 30(10): 1213-1230. |
| [6] | Goodwin G C, Agüero J C, Cea G, et al. Sampling and sampled-data models[J]. IEEE Control System Magazine, 2013, 10(1): 34-54. |
| [7] | Lindorff D P. Theory of sampled-data control systems[D]. New York, USA: Wiley, 1965. |
| [8] | Hagiwara T, Araki M. Properties of limiting zeros of sampled systems[J]. Transactions of the Institute of Electrical Engineers of Japan, 1990, 110(4): 235-244. |
| [9] | Zeng C, Liang S. Zero dynamics of sampled-data models for nonlinear multivariable systems in fractional-order hold case[J]. Applied Mathematics and Computation, 2014, 246(1): 88-102. |
| [10] | Ishitobi M, Koga T, Nishi M, et al. Asymptotic properties and stability criteria of zeros of sampled-data systems[C]//49th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2010, 4952-4957. |
| [11] | Ishitobi M, Nishi M, Kunimatsu S. Asymptotic properties and stability criteria of zeros of sampled-data models for decouplable MIMO systems[J]. IEEE Transactions on Automatic Control, 2013, 58(11): 2985-2990. |
| [12] | Ugalde U, Bárcena R, Basterretxea K. Generalized sampled-data hold functions with asymptotic zero-order hold behavior and polynomic reconstruction[J]. Automatica, 2012, 48(9): 1171-1176. |
| [13] | 梁山, 石飞光章, 石卫人, 等. 离散时间MIMO系统极限零点的稳定性[J]. 自动化学报, 2007, 33(4): 439-442. Liang S, Ishitobi M, Shi W R, et al. On stability of the limiting zeros of discrete-time MIMO systems[J]. Acta Automatica Sinica, 2007, 33(4): 439-442. |
| [14] | Yuz J I, Goodwin G C. On sampled-data models for nonlinear systems[J]. IEEE Transactions on Automatic Control, 2005, 50(10): 1477-1489. |
| [15] | Zeng C, Liang S, Li H B. Asymptotic properties of zero dynamics for nonlinear discretized systems with time delay via Taylor method[J]. Nonlinear Dynamics, 2014, 78(3): 13-25. |
| [16] | Yuz J I, Goodwin G C. Sampled-data models for linear and nonlinear systems[M]. Berlin, Germany: Springer-Verlag, 2014. |
| [17] | Yurca E A, Yuz J I, Goodwin G C. Sampling zeros of discrete models for fractional order systems[J]. IEEE Transactions on Automatic Control, 2013, 58(11): 2383-2388. |
| [18] | Liang S. Studies on stability of zeros of discrete-time control system[D]. Kumamoto, Japan: Kumamoto University, 2004. |
| [19] | Khalil H. Nonlinear systems[M]. 3rd ed. London, UK: Prentice-Hall, 2002. |
| [20] | Isidori A. Nonlinear control systems: An introduction[M]. 3rd ed. Berlin, Germany: Springer-Verlag, 1995. |
| [21] | Ishitobi, Nishi M. Zero dynamics of sampled-data models for nonlinear systems[C]//2008 American Control Conference. Piscataway, NJ, USA: IEEE, 2008: 1184-1189. |