文章快速检索  
  高级检索
引用本文
郝立瑛, 戴芳, 高雄飞. 基于（2D）2-KL变换的小波域图像融合算法[J]. 信息与控制, 2015, 44(3): 334-338,345
HAO Liying, DAI Fang, GAO Xiongfei. Image Fusion Algorithm Based on the (2D)2-KL Transform in Wavelet Domain[J]. INFORMATION AND CONTROL, 2015, 44(3): 334-338,345.
基于（2D）2-KL变换的小波域图像融合算法
郝立瑛1, 戴芳1, 高雄飞2    
1. 西安理工大学理学院, 陕西 西安 710054;
2. 长安大学理学院, 陕西 西安 710064
收稿日期: 2014-05-27; 录用日期: 2014-08-20; 修回日期: 2014-08-26
基金项目：国家重大研究计划培育项目（91120014）；陕西省教育厅科研计划资助项目（12JK0534）.
作者简介: 郝立瑛（1990-），女，硕士生．研究领域为图像处理，图像融合．
戴芳（1966-），女，博士，教授，硕士生导师．研究领域为图像处理，统计计算．
高雄飞（1988-），男，硕士生．研究领域为智能优化算法，水文地质的数学方法．
通讯作者：郝立瑛，xaut_hly@163.com
摘要：为使融合后的图像在尽可能保留源图像细节信息的同时，还能够有效提高源图像的对比度，提出基于（2D）2-KL（（2D）2-Karhunen-Loeve）变换的小波域图像融合算法．首先用（2D）2-KL变换直接对图像信息进行分析，并构建协方差阵，提取图像的重要特征，然后将其主要特征输入到小波域中．在此基础上，对小波变换分解得到各子带系数，用一定的融合策略进行融合．低频子带含有图像的轮廓信息，引入加权因子指导低频子带系数进行融合．实验结果表明，提出的算法有效提高了图像的对比度，并且很好地保留了图像的细节信息，无论在视觉角度上，还是在各种客观性能评价上都比其它传统方法取得了更佳的融合效果．
关键词： （2D）2-KL（（2D）2-Karhunen-Loeve）变换     小波域     图像融合    
Image Fusion Algorithm Based on the (2D)2-KL Transform in Wavelet Domain
HAO Liying1 , DAI Fang1, GAO Xiongfei2     
1. School of Science, Xi'an University of Technology, Xi'an 710054, China;
2. College of Science, Chang'an University, Xi'an 710064, China
Abstract:An image fusion algorithm based on the (2D)2-KL transform in a wavelet domain is proposed, aiming at reserving the details of the original images after image fusion and improving the contrast of the original images. First, (2D)2-KL transform is used to analyze the information directly and the covariance matrix is constructed to obtain the significant features. Then, the significant features are transmitted into the wavelet domain. On this basis, certain fusion strategies are utilized for each subband coefficient of the wavelet decomposition. The low frequency subband contains the contour information of the image, and therefore, the weighting factors are employed to fuse the low-frequency coefficient. Finally, experiments show that the proposed method can not only effectively improve the contrast of the image, but also retain the image details. By comparing human perceptions and conducting various objective performance evaluations, the proposed method is shown to perform better than conventional approaches.
(2D)2-KL((2D)2-Karhunen-Loeve) transform     wavelet domain     image fusion    

1 引言

在图像理解和计算机视觉领域中，图像融合技术已成为研究和发展的一个重要方向. 图像融合技术在自动目标识别[1, 2]、 医疗诊断[3, 4]、 智能车辆以及遥感领域有着广泛的应用[5, 6, 7]. 图像融合技术是将多个传感器在同一时间或不同时间获取的关于某个目标的图像序列信息加以处理，生成一幅满足某种需求的新图像.融合图像综合了各图像的互补信息和冗余信息，比原来任何一幅图像信息都更为丰富，对目标的表征也更为精确. 目前，常用的图像融合算法有加权平均法、 塔式分解法[8, 9, 10]及智能优化算法[11, 12, 13]. 这些方法取得了一定的融合效果，但分解过程会产生冗余，图像的许多重要细节信息会丢失，致使融合图像分辨率低、 对比度不足. 随着小波变换的不断发展，Mallat[14]提出的小波变换算法对图像进行了不同尺度的分解，并没有引起数据量的增加，滤波器系数对任意两相邻尺度均保持恒定. 小波变换使图像信息集中在少数几个变换系数上，能有效提取图像水平、 垂直和对角3个方向的细节特征. Yang[15]首次提出2D-KL变换解决了在人脸识别中由1D-KL变换引起的维数灾难. 与1D-KL变换不同，2D-KL变换不需要将图像转换为一维向量，克服了1D-KL变换难以准确评估协方差阵的缺点. 之后，

Zhang[16]提出的(2D)2-KL变换通过向坐标轴投影同时获得图像行、 列两个方向的特征，有效提取了源图像丰富的信息，能更精确计算协方差阵，缩短了运算时间，使得运行效率明显提高. 本文充分利用(2D)2-KL变换与小波变换在图像融合中所表现出的优良特性，将两者相结合，提出基于(2D)2-KL变换的小波域图像融合算法. 实验结果表明，提出的算法有效提取了图像的重要特征，融合图像的边缘细节信息更为显著，更加突出了目标的重要信息.

2 (2D)2-KL变换

(2D)2-KL变换是一种直接基于二维图像的投影方法，用图像矩阵直接构建协方差阵，并求此协方差阵的特征值和特征向量，最后将较大特征值所对应的特征向量向坐标轴投影，从而得到图像的重要特征.

设样本图像集为T=｛A1，A2，…，AN｝，每个Ap为m×n的矩阵(p=1，2，…，N)，由文[16]可知样本图像的协方差阵为

其中，代表样本的均值.此时，最优投影向量为S的d个较大特征值对应的相互正交的特征向量x1，x2，…，xd，即它们组成最优投影矩阵Xopt=[x1，x2，…，xd].

令Ap=[(A(1)p)T (A(2)p)T… (A(m)p)T]T，A=[(A(1))T(A(2))T…(A(m))T]T，A(i)p和A(i)分别表示Ap和A的第i个行向量，则式(1)可表示为

式(2)表明图像的协方差阵可由图像的行向量产生，也就是说上述得到的最优投影矩阵Xopt反映了图像在行方向的主要特征. 同样，通过类似上述方法得到图像在列方向的最优投影阵. 设Ap=[(A(1)p)(A(2)p)…(A(m)p)]，A=[(A(1))(A(2))…(A(m))]，A(j)p和A(j)分别表示Ap和A的第j个列向量，则列方向上样本图像的协方差阵为

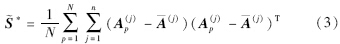
为得到列方向的最优投影矩阵，定义如下准则：

式中，M*为投影特征矩阵M的协方差阵，tr(M*)为M*的迹. 通过线性变换M=WTA将图像矩阵A投影到WT上，即得到投影特征矩阵M. 为便于表示，这里的A指样本图像集T中任意一个m×n的子图像. 样本图像的总散度可以度量W中每个向量的区分能力，所有样本图像的总散度用M*的迹表征. 求式(4)的最大值确定最优投影矩阵Wopt，则：

此时，样本图像的协方差阵为

于是图像在列方向上的最优投影矩阵由S*的d个较大特征值对应的相互正交的特征向量组成，即Wopt=[w1，w2，…，wd]. Wopt反映了图像在列方向的主要特征. 当d=m时，所有的特征向量组成投影矩阵W. 得到了图像行方向的最优投影矩阵Xopt和列方向的最优投影矩阵Wopt，对图像进行特征提取，得其特征矩阵：

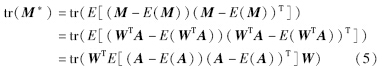
其中，C为d×d的对角阵，主对角线上的元素为(k=1，2，…，d)，λk为S*的特征值，取其d个较大特征值. 特征矩阵Z包含了图像在行、 列两个方向的最优投影特征，因此称为(2D)2-KL变换，提取了源图像更多的信息.

3 基于(2D)2-KL变换的小波域图像融合算法

3.1 图像的二维离散小波变换

小波变换提供了一种数据表示和分析方式，它的函数基由一个称为母小波的函数通过膨胀和平移获得，具有时频局部化性质和多分辨率分析能力.图像是二维信号，在数值计算时需要对小波变换的尺度因子和位移因子进行离散化，即离散小波变换(discrete wavelet transform，DWT). 对任意二维图像c(m，n)，由文[14]知离散小波变换分解如下：

其对应的重构过程为

其中，h和h为低通滤波器，g和g为高通滤波器. cj+1代表图像在本层分辨率下的低频分量，D1j+1、 D2j+1和D3j+1分别代表图像的水平高频分量、 垂直高频分量和对角高频分量.

3.2 图像融合新算法

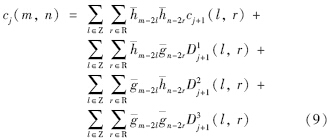
基于(2D)2-KL变换的小波域图像融合算法主要步骤如下：

Step 1： 对源图像A1用DWT分解得到4个子图像，分别提取其低频子带系数cj和高频子带系数DJε(ε=1，2，3)，J表示对图像进行两层DWT分解，ε为高频系数3个子带方向.

Step 2： 对与A1相融合的源图像A2通过(2D)2-KL变换投影得到特征矩阵Z，对特征矩阵Z进行DWT两层分解.

Step 3： 将Step 1和Step 2经DWT分解得到的高频子带系数采用式(11)～(15)融合策略进行融合，低频子带系数用式(10)融合策略进行融合，得到融合图像F1的小波系数.

Step 4： 对F1的小波系数进行一致性效验，保证窗口区域(3×3窗口)中心位置的融合系数与其周围邻域内绝大多数的融合系数取自同一图像的子带.

Step 5： 对融合后的子带系数进行DWT逆变换，得到最终的融合图像F2.

上述融合算法中，高、 低频子带系数的融合对融合结果有着重要的影响. 低频系数含有图像的概貌信息，因此，引入加权因子α1、 α2指导低频系数进行融合，定义：

其中，fi(i=A，B)为待融合的低频系数，fF为融合系数. 特征矩阵已包含图像的大部分信息，对其经DWT分解得到低频子带系数fA引入加权因子α1，与此同时对与其待融合的低频子带系数fB引入加权因子α2. 经过实验验证表明，当α1=0.8且α2=0.2时，低频系数的融合效果最优，进一步突出了图像的重要特征. 该融合策略很好地保留了图像的主要结构信息.图像的纹理、边缘细节信息多集中在高频子带中，再考虑到图像邻域像素与像素之间相关性较大，为此图像高频子带系数的融合依据邻域能量活性测度准则[17]. 定义以(m，n)为中心N×N的窗口(一般为3×3或5×5)，本文选取3×3的窗口，窗口区域能量活性测度[17]为

其中，J表示对图像进行两层DWT分解，QJε，k(k=A，B)代表分解后的各高频子带系数，p(i，j)为权系数，满足.

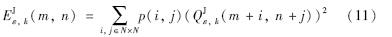
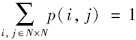窗口区域系数归一化相关函数为

对于给定的阈值T(T∈｛0，1｝)，本文T=0.8，如果RJε小于T，按下式准则融合：

其中，QJε，F表示融合系数. 如果RJε大于等于阈值T，则融合准则为

式中，

4 实验结果及分析

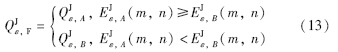
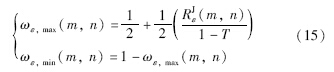
选用3组图像(Barbara图像、 Boat图像、 Clock图像)进行实验，如图 1～3所示. 为验证本文算法的有效性，采用两种方法进行实验对比，即离散小波变换(DWT)融合算法(算法1)和空间域加权平均融合算法(算法2). DWT算法中，低频系数采用加权平均的融合准则，高频系数用绝对值取大融合准则. 小波基选择“db4”，分解层数为两层. 实验对一幅图像进行(2D)2-KL变换，第2节的指A2所有元素和的平均值.

图 1 Barbara源图像Fig. 1 Barbara source images
图选项

图 2 Boat源图像Fig. 2 Boat source images
图选项

图 3 Clock源图像Fig. 3 Clock source images
图选项

从视觉角度来看，本文算法得到的图像融合效果对比度更强，边缘细节信息更清晰. 如图 4，Barbara图中左上角排列的一排书，本文算法的融合图像(图 4(a))可以清晰地分辨书与书之间的边缘细节，而算法1和算法2融合图像(图 4(b)和图 4(c))书的边缘较模糊. 图 5中，Boat图像从左边起第2艘船底与水面衔接的部分，本文算法(图 5(a))的融合图像显然更清晰地展现了许多细节信息，算法1和算法2的融合图像(图 5(b)和图 5(c))有相互混合重叠的现象. 再如Clock图像(图 6)，无论是小钟表的细微刻度，还是大钟表的数字刻度，本文算法的融合图像(图 6(a))均优于另外两种算法的融合图像(图 6(b)和图 6(c)).

图 4 Barbara图像不同融合算法融合结果Fig. 4 The fused results of Barbara image using different algorithms
图选项
图 5 Boat图像不同融合算法融合结果Fig. 5 The fused results of Boat image using different algorithms
图选项
图 6 Clock图像不同融合算法融合结果Fig. 6 The fused results of Clock image using different algorithms
图选项

以上是从视觉角度来分析评价不同算法的融合效果，为定量分析不同融合算法的性能，采用空间频率(spatial frequency，SF)，平均梯度(average gradient，AG)和峰值信噪比(peak signal to noise ratio，PSNR)[18, 19, 20]3个指标进行客观评价. 这3个评价指标值越大，融合效果越好，融合图像信息越丰富.

由表 1~3可见，本文算法的空间频率SF和平均梯度AG均大于算法1和算法2，表明本文算法的空间域总体活跃程度较大，图像的细节和纹理特征都得到很好的保留，所以融合图像更清晰. 在PSNR方面，由表 1~3可知，本文算法得到的PSNR均大于算法1和算法2，表明本文算法有力地提取了图像的重要特征，进一步改善了图像质量.

表 1 Barbara图像不同融合算法评价指标 Tab. 1 Evaluation index of different fusion algorithms of Barbara image
算法SFAGPSNR
本文算法17.770 37.924 224.149 5
小波算法14.953 86.833 022.356 2
加权平均法11.805 65.551 821.984 9

表选项

表 2 Boat图像不同融合算法评价指标 Tab. 2 Evaluation index of different fusion algorithms of Boat image
算法SFAGPSNR
本文算法18.603 6 8.117 5 24.166 8
小波算法15.280 06.593 9 22.571 8
加权平均法12.063 95.295 322.261 9

表选项

表 3 Clock图像不同融合算法评价指标 Tab. 3 Evaluation index of different fusion algorithms of Clock image
算法SFAGPSNR
本文算法19.420 9 7.273 4 24.391 3
小波算法17.663 96.129 4 23.810 5
加权平均法13.123 95.061 1 23.025 7

表选项

根据以上分析本文算法的空间频率SF、 平均梯度AG及峰值信噪比PSNR 3个指标均大于小波算法和加权平均法，与目视结果一致，表明本文算法取得了更优的融合效果.

5 结论

小波变换的多尺度性和多方向性能很好地保留图像的边缘信息，本文将(2D)2-KL变换与小波变换相结合，提出了一种新的图像融合算法.同时，针对低频子带系数引入加权因子，突显了图像的重要特征. 根据高频子带系数的特征，采用基于邻域能量活性测度的融合策略，显著提高了图像邻域像素的相关性. 与经典的离散小波变换算法和空间域加权平均融合算法性能比较中，本文算法在增强融合图像细节表现力的同时提高了融合图像的对比度，是一种有效的融合算法.

参考文献
[1] Yang A Y, Maji S, Hong K, et al. Distributed compression and fusion of nonnegative sparse signals for multiple-view object recognition[C]//12th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2009: 1867-1874.
[2] Praveen K, Ankush M, Padam K. Addressing uncertainty in multi-modal fusion for improved object detection in dynamic environment[J]. Information Fusion, 2010, 11(4): 311-324.
[3] Pizzi M N, Bruix S A, Calabria H C, et al. Image fusion of gated SPECT and CT angiography in coronary artery disease[J]. Revista Espanola de Medicina Nuclear, 2010, 29(6): 299-303.
[4] Bai X Z, Zhou F G, Xue B D. Image fusion through local feature extraction by using multi-scale top-hat by reconstruction operators[J]. Optik, 2013, 124(18): 3198-3203.
[5] McAlpin D, Meyer F J. Multi-sensor data fusion for remote sensing of post-eruptive deformation and depositional features at Redoubt Volcano[DB/OL]. (2012-08-23)[2013-09-15]. http://www.elsevier.com/locate/jvolgeores.
[6] Dong Z Y, Wang Z M, Liu D W, et al. SPOT5 multi-spectral (MS) and panchromatic (PAN) image fusion using an improved wavelet method based on local algorithm[DB/OL]. (2013-07-13)[2013-09-15]. http://www.elsevier.com/locate/cageo.141.
[7] 赵永强, 潘泉, 张洪才. 一种新的全色图像与光谱图像融合方法研究[J]. 光子学报, 2007, 36(1): 180-183. Zhao Y Q, Pan Q, Zhang H C. A new spectral and panchromatic images fusion method[J]. Acta Photonica Sinica, 2007, 36(1): 180-183.
[8] 汤磊, 赵丰, 赵宗贵. 基于非下采样Contourlet变换的多分辨率图像融合方法[J]. 信息与控制, 2008, 37(3): 291-297. Tang L, Zhao F, Zhao Z G. Multi-resolution image fusion based on the nonsubsampled Contourlet transform[J]. Information and Control, 2008, 37(3): 291-297.
[9] 周厚奎. 基于静态小波变换和2代曲波变换的图像融合算法[J]. 信息与控制, 2012, 41(3): 278-282. Zhou H K. An image fusion method based on the second generation curvelet and stationry wavelet transform[J]. Information and Control, 2012, 41(3): 278-282.
[10] Zhao H, Li Q, Feng H J. Multi-focus color image fusion in the HSI space using the sum-modified-Laplacian and a coarse edge map[J]. Image and Vision Computing, 2008, 26(9): 1285-1295.
[11] Chen R Y, Li S, Yang R. Remote sensing image fusion based on data assimilation and genetic simulated annealing algorithm[C]//International Symposium on Information Science and Engineering. Piscataway, NJ, USA: IEEE, 2008: 520-524.
[12] 田霞, 雷秀娟. 免疫粒子群优化算法在图像融合中的应用[J]. 计算机工程与应用, 2009, 45(5): 167-170. Tian X, Lei X J. Application of immuse particle swarm optimization algorithm in image fusion[J]. Computer Engineering and Applications, 2009, 45(5): 167-170.
[13] 张新曼, 韩九强, 王勇. 一种遗传搜索块寻优的不同聚焦点图像融合算法[J]. 电子与信息学报, 2006, 28(11): 2054-2057. Zhang X M, Han J Q, Wang Y. A multifocus image fusion algorithm for adaptive genetic search[J]. Journal of Electronics & Information Technology, 2006, 28(11): 2054-2057.
[14] Mallat S G. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693.
[15] Yang J, Zhang D. Two-dimensional PCA: A new approach to appearance-based faces representation and recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137.
[16] Zhang D Q, Zhou Z H. (2D)2PCA: Two-directional two-dimensional PCA for efficient face representation and recognition[J]. Neurocomputing, 2005, 69(3): 224-231.
[17] Burt P J, Kolczynski R J. Enhanced image capture through fusion[C]//Proceedings of the Fourth International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 1993: 173-182.
[18] 李树涛, 王耀南, 张昌凡. 多传感器图像融合的客观评价与分析[J]. 仪器仪表学报, 2002, 23(6): 651-654. Li S T, Wang Y N, Zhang C F. Objective evaluation and analysis of multisensory image fusion[J]. Chinese Journal of Scientific Instrument, 2002, 23(6): 651-654.
[19] Huang W, Jing Z L. Evaluation of focus measures in multi-focus image fusion[J]. Pattern Recognition Letters, 2007, 28(4): 493-500.
[20] Yakhdani M F, Azizi A. Quality assessment of image fusion techniques for multisensory high resolution satellite images[R]. Vienna, Austria: International Archives of Photogrammetry and Remote Sensing, 2010: 204-209.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0334
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

郝立瑛, 戴芳, 高雄飞
HAO Liying, DAI Fang, GAO Xiongfei
基于（2D）2-KL变换的小波域图像融合算法
Image Fusion Algorithm Based on the (2D)2-KL Transform in Wavelet Domain
信息与控制, 2015, 44(3): 334-338,345.
INFORMATION AND CONTROL, 2015, 44(3): 334-338,345.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0334

文章历史

收稿日期：2014-05-27
录用日期：2014-08-20
修回日期：2014-08-26

工作空间