2. 华南理工大学自动化科学与工程学院, 广东 广州 510640
2. School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China
1 引言
采用活性污泥实现污水生化处理是一种被公认的最经济且具有可持续发展的城市生活污水处理方法[1]. 为了保证污水处理厂连续稳定的运行，保证处理过的出水水质满足规定的要求，并且尽可能节省污水处理过程的运行代价，国内外学者在污水处理运行过程的控制器设计、 参数优化等方面展开了广泛的研究. 文[2]针对污水生化处理过程模糊控制器的参数设定问题，研究出一套系统的调整方法，提高了控制器运行效果； 文[3]研究了出水氨氮浓度反馈控制器的参数取值大小与污水出水水质之间的关系； 文[4, 5, 6]通过综合污水处理过程运行能耗，并对出水水质越限进行一定程度的惩罚作为优化目标，分别采用了遗传算法、 蛙跳粒子群算法等智能优化算法，求取在目标函数为极值条件下的污水处理过程好氧池末端溶解氧浓度(SO，5)和厌氧池末端硝酸氮浓度(SNO，2)控制器的设定值，最终提高污水生化处理过程的运行效率； 然而，污水生化处理过程的运行效果体现为多目标的，这些目标函数常常具有不同的物理量标定并且是相互制约的，单纯的将多个目标函数叠加较难有效地反映系统运行的性能. 针对这个问题，文[7]研究了如何更有效地综合不同运行目标最终形成单一的运行代价函数，作为衡量众多不同控制结构或不同控制参数取值下系统运行性能的一种工具； 文[8]在文[7]的研究基础上，提出了一种适合不同容量的污水处理厂，综合污水生化处理过程多目标的评价方法，采用遗传算法、 单纯形法及模式搜索法优化污水处理过程控制器的设定值，分析了不同设定值下污水生化处理系统的运行效果.
本文通过学习蛙跳算法[9]模因进化机制，提出了一种改进的差分进化算法，在4个典型函数上进行寻优实验，仿真结果验证了该算法的寻优性能，然后以文[8]提出的污水生化处理过程的评价方法作为目标函数，在开放的污水处理过程仿真基准模型(benchmark simulation model No.1，BSM1)[10]的平台上，将所提出的改进差分进化算法应用到对污水生化处理过程常用的几个控制回路中(好氧池溶解氧浓度(SO，5)控制回路、 厌氧池硝酸氮浓度(SNO，2)控制回路、 好氧池末端悬浮物浓度(SS5)控制回路、 污泥回流比(r)控制回路等)，实现对污水生化处理过程被控变量的设定值进行寻优计算； 最后仿真了4种不同的控制策略在3种不同天气入水条件下的污水生化处理过程，结果表明了基于改进差分进化算法的污水生化处理优化控制不仅可以降低系统运行代价，还可以缩短关键出水水质变量的越限时间长度，提高出水水质.
2 活性污泥法污水处理过程控制优化 2.1 活性污泥法污水处理过程前置反硝化工艺的污水处理过程是实现城市生活污水处理的最常用方式. 这类污水生化处理过程必须保证是连续运行的，并且希望利用尽可能少的运行代价保证出水水质满足各项规定要求. 针对这些问题，国内外专家研究了很多不同的控制策略，为了公平地评价不同的控制策略，国际水协会(international water association，IWA)与欧盟科学技术合作组织(european co-operation in the field of scientific and technical research，COST)，建立了开放的污水处理过程仿真基准模型(BSM1)，它定义了前置反硝化污水生化处理的设备布局、 仿真模型、 评价标准等. 图 1显示了BSM1的设备总体布局，它由2个缺氧池、 3个好氧池和1个沉淀池构成. 在好氧池内通过曝气作用(KLa)为硝化细菌吸附有机物作为营养源提供好氧条件，实现了氨氮转化为亚硝酸氮和硝酸氮，接着通过混合液回流(Qint)，使得硝酸盐在缺氧池中经过反硝化细菌的作用转化为氮气和水，污水经过缺氧与好氧共5个反应池的生化反应后在沉淀池进行污泥沉淀，最上层的上清液作为处理后的出水排入受纳水体，最底层的污泥一部分通过回流(Qr)转移至第一个反应池得以重复利用，另一部分通过控制污泥排放量(Qw)，将剩余污泥进行下一步的污泥处理.
 |
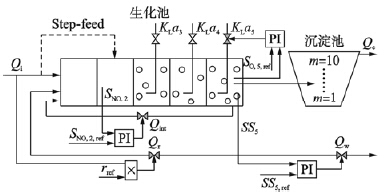| 图 1 BSM1设备示意图Fig. 1 Overview of the BSM1 plant |
对污水生化处理过程的控制常常通过控制系统中的一些变量达到某设定值来实现的，图 1显示了BSM1中常用的几个自动控制回路： 通过控制好氧池末端的曝气量(KLa5)维持好氧池中的溶解氧浓度(SO，5)； 通过控制内回流量(Qint)保证缺氧池中的硝酸盐浓度(SNO，2)； 通过控制污泥排放量(Qw)来维持好氧池末端的悬浮物浓度(SS5)； 污泥外回流量(Qr)常常保持与入水流量(Qi)成比例r的控制； 当入水流量超过平均流量(Qave=18 446 m3·h-1)的两倍时，为了避免由于过大的水力负荷导致沉淀池过载，通过旁路将多余的流量直接引至第2个反应池(step-feed)，等等.在实际污水生化处理过程，这些控制器的设定值通常依据运行人员经验取值，这样的设定值难以保证系统维持较低的运行代价.
本文提出一种改进的差分进化算法，选择一种综合污水生化处理出水水质、 曝气能耗、 泵送能耗和污泥处理费用等方面的函数作为优化目标，根据污水处理厂的入水情况优化污水处理过程中自动控制回路的控制器设定值SO，5，ref、 SNO，2，ref、 SS5，ref、 rref，以提高系统运行效率为目的.
本文选择的优化目标函数[8]为
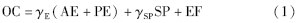
差分进化算法(DE)是由Storn和Price提出的一种基于群体演化的优化算法[11].它采用实数编码形式产生候选解，通过差分变异、二元交叉、贪心选择3种操作进行最优解的探索过程，是一种全局优化性能和数值稳定性都非常出色的算法[12]. 然而和很多智能算法一样，基本的DE算法在寻优过程也常常因为种群多样性的缺失，导致算法过早收敛，难以求取到更优秀的解.
近20年来很多学者通过不同的方式改进基本DE算法，以提高算法的寻优性能,如： 通过与其它算法进行混合，取长补短以提高改进算法的性能[13, 14]； 通过改进DE的操作算子以提高算法的寻优能力[15, 16],等等. 在前人的研究基础上及受蛙跳算法的迭代过程[9](分模因组—不同模因组独立进化—混合模因组，如此反复迭代进化计算机制)的启发，本文提出了一种改进DE算法，即采用DE算法作为进化过程的计算方法，引入蛙跳算法中模因进化模式，促进种群中的个体有效地学习局部最优个体和全局最优个体的信息，引导算法迅速有效地搜索更精确的解. 该算法应用到污水生化处理过程设定值优化的步骤描述如下：
Step 1： 根据待优化设定值的取值范围，随机产生NP个D维的解作为初始种群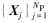
； 初始化总进化代数Iitermax，子种群进化代数Iiter，种群分割次数Cn=Iitermax/Iiter.
Step 2： 将种群P随机平均分割成Nk个子种群Pk.
Step 3： 针对每个子种群Pk，按照Step 3-1至Step 3-3循环计算Iiter代：
Step 3-1： 对子种群Pk中的每个解向量Xi，选择“DE/rand/2”差分变异策略[17]产生变异向量Vi：
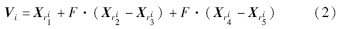
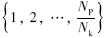中随机取出的两两不相同的随机数且与i不同； 缩放因子F是一个正的控制参数，用来控制差异向量的长度. Step 3-2： 采用二元交叉操作作用于变异向量Vi和对应的原解向量Xi，产生最终的试探解Ui=(ui1，…，uiD)：
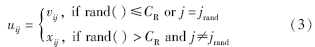
Step 3-3： 将试探解Ui与原解Xi分别作为污水生化处理过程控制器的设定值，选择特定天气下的入水数据进行仿真，根据式(1)计算对应解的适应度值，最后选择两者中适应度值较小的作为新解Xi，保留到DE算法的下一代.
Step 4： 混合Nk个子种群获得新种群P，判断子种群混合次数是否达到Cn次，如果否，转Step 2； 如果是，转Step 5.
Step 5： 算法停止.
3 仿真研究 3.1 典型函数仿真实验为了验证本文所提出的IDE算法的寻优性能，本文选择了4个典型的函数[17]，具体描述如下：
F1： Rosenbrock
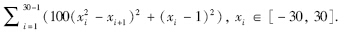
F2： Shifted Sphere
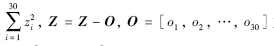
∑30i=1z2i，Z=Z-O，O=[o1，o2,…，o30]为新的最优值，xi∈[-30, 30].
F3： Shifted Rotated Schwefel
，
，
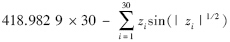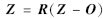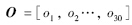，R为单位正交矩阵，xi∈[-30, 30].
F4： Composition Function
复合函数中包含10个典型函数，具体描述见文[17]中的f14.
本文在上述4个典型函数上分别仿真了差分变异策略为DE/rand/1(DE1)，DE/best/1(DE2)，DE/best/2(DE3)，DE/rand/2(DE4)4种基本DE算法和本文提出的IDE算法. 基本DE算法DE1、 DE2、 DE3和DE4的变异算子详见文[17]中的式(2)、 (3)、 (5)和式(6)，算法参数设置为DE1、 DE4、 IDE： F=0.5，CR=0.3； DE2、 DE3： F=0.9，CR=0.6； 本文提出的IDE算法中子种群数设置为Nk=5，Iiter=10. 在仿真实验中不同算法设定相同的种群规模，即NP=20； 相同的算法迭代代数Iitermax=5 000次； 每种算法对每个典型函数均寻优计算20次，通过求平均值以获得随机算法的平均寻优结果.
表 2列出了5种算法在4个典型函数上寻优计算的平均最优值和均方差，图 1(a)和图 1(b)两个子图画出了5种算法在4个典型函数上寻优的平均最优值随代数的变化情况(为了方便曲线显示，将平均最优值加0.001后取ln运算).
| 性能 | CS1 | CS2 | CS3 | CS4 |
| OC /(＄·m-3) | 11 514 | 7 221 | 6 061 | 6 041 |
| SP /(kg·d-1) | 2 441 | 2 117 | 2 031 | 2 042 |
| AE /(kW·h·d-1) | 7 238 | 7 371 | 6 799 | 6 904 |
| PE /(kW·h·d-1) | 1 502 | 2 034 | 2 717 | 2 533 |
| EF /(kW·h·d-1) | 9 420 | 5 222 | 4 094 | 4 076 |
| ％Tviol.CODe | 0 | 0 | 0 | 0 |
| ％Tviol.Ntot，e | 17.6 | 0.6 | 0 | 0 |
| ％Tviol.SNH，e | 17.3 | 3.9 | 10.0 | 6.4 |
| ％Tviol.SSe | 0 | 0 | 0 | 0 |
表 1及图 2的仿真结果显示，从算法的寻优精度方面上看，IDE算法在4个典型函数上的寻优结果均优于4种基本DE算法，特别是F1、 F2和F4； 从算法跳出极值能力方面来看，DE1和DE2在4个典型函数的寻优过程中都很快就陷入局部极小值，在算法寻优期间所起作用的时域非常短； DE3在F1和F3两种函数寻优过程可以缓慢跳出局部极小值，DE4在F4函数寻优过程具有一定的搜索能力，而本文提出的IDE算法在迭代过程能不断地跳出局部极小值寻找到更精确的解，具有很好的搜索能力. 总之，本文提出的IDE算法可以平衡智能优化算法的寻优精度与收敛速度两个要素，相比4种基本DE算法在寻优性能上有了明显的提高.
| 函数 | 性能 | DE1 | DE2 | DE3 | DE4 | IDE |
| F1 | 均值 | 5.844e+06 | 4.097e+05 | 4.037e+06 | 2.146e+06 | 3.920e+01 |
| 方差 | 5.452e+06 | 4.047e+05 | 2.825e+06 | 1.605e+06 | 3.153e+01 | |
| F2 | 均值 | 6.523e+02 | 1.891e+02 | 7.805e+02 | 3.946e+02 | 1.154e-30 |
| 方差 | 2.418e+02 | 1.671e+02 | 2.329e+02 | 1.359e+02 | 1.313e-30 | |
| F3 | 均值 | 1.203e+04 | 1.202e+04 | 1.201e+04 | 1.206e+04 | 1.196e+04 |
| 方差 | 2.402e+01 | 3.336e+01 | 3.817e+01 | 3.184e+01 | 2.563e+01 | |
| F4 | 均值 | 9.624e+02 | 9.011e+02 | 8.877e+02 | 9.706e+02 | 4.445e+02 |
| 方差 | 9.141e+01 | 7.006e+01 | 1.035e+02 | 6.383e+01 | 3.441e+01 |
 |
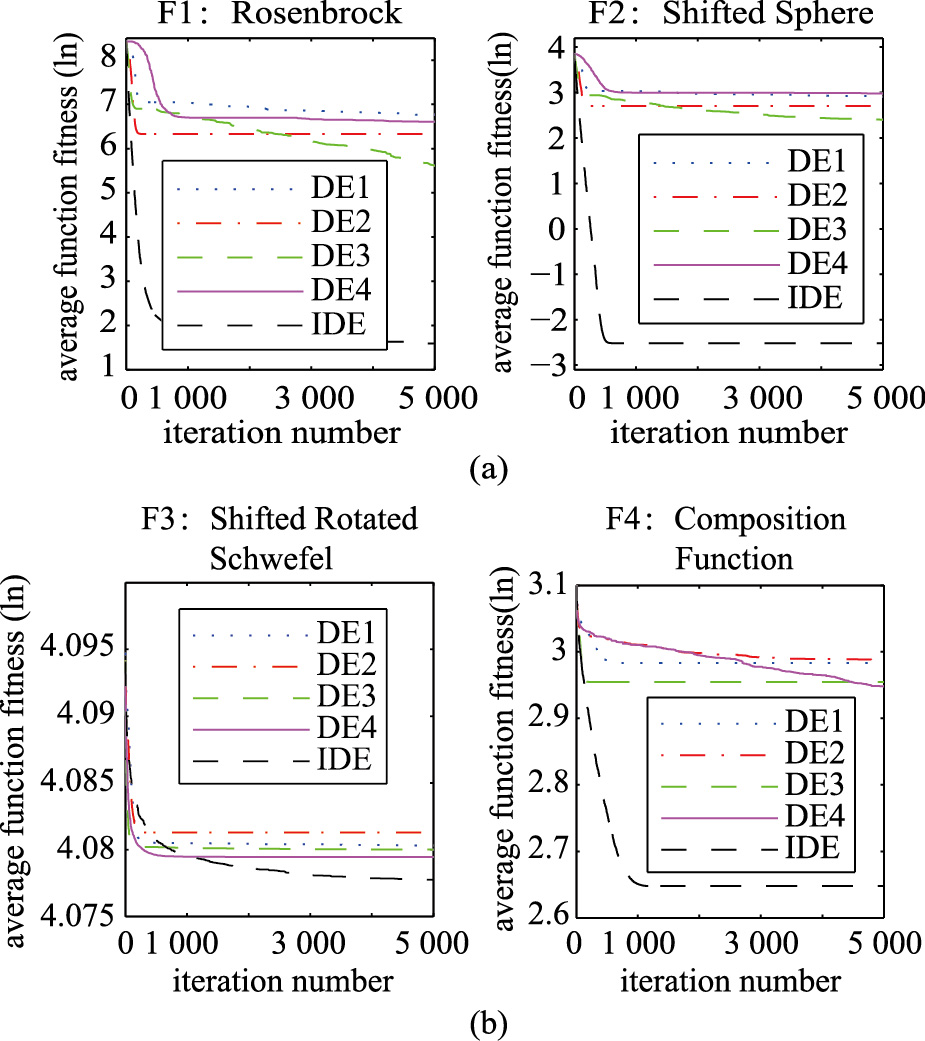| 图 2 平均最优值变化过程Fig. 2 Change process of average optimal value |
为了验证本文所提出的IDE算法应用到污水生化处理过程设定值优化的运行效果，本文在BSM1平台上进行了大量的仿真实验.首先，污水入水数据采用了COST提供的晴天(DRY)、雨天(RAIN)、暴雨天(STORM)3种天气条件下的城市生活污水数据集，它们均由真实操作采集到的，历时均为两周(0 d～14 d).
接着，设置关键优化条件. 参照文[18]的式(1)，设定值的寻优范围定为： SO，5，ref∈[0.5，2]，SNO，2，ref∈[0.5，2]，SS5，ref∈[4 000，5 000],单位为(g·m-3)； rref∈[0.5，1.5].
控制器参数设定： SO，5控制器： Kp=500 d-1·(g·m-3)-1，Ti=0.001 d； SNO，2控制器： Kp=15 000 d-1·(g·m-3)-1，Ti=0.05 d； SS5控制器： Kp=-0.2 d-1·(g·m-3)-1，Ti=18 d.
在优化周期方面，由COST提供的3种天气条件下的入水流量浓度变化情况可知，周内(周一至周五)的每一天入水情况变化呈现以天为单位的同一类周期性，周末(周六至周日)两天呈现出与周内不同的周期性变化，根据该特点，本文实验了两种不同的优化周期情况： 一种是不考虑周内与周日条件的变化，将优化周期设定为周一至周日； 另一种是依据周内与周末两种明显不同的入水模态，将优化周期分段为周内和周末两段.
实验中IDE算法的迭代代数Iitermax=30，算法其它参数设置与2.1节相同. 寻优计算过程，为了保证求解的一致性，先在入水条件不变的情况下进行开环控制的稳态仿真100 d，然后运行2周的晴天条件下的入水数据，以此刻的污水生化处理过程各变量值作为寻优计算的初始状态，求解控制器最优设定值.
最后，本文仿真了不同入水条件下，采用所提出的IDE算法进行寻优计算，获得目标函数为极值条件下的SO，5，ref、 SNO，2，ref、 SS5，ref，rref值，仿真结果表明本文所提出算法在不同的入水条件下均可以达到较好的运行效果. 本文选择暴雨天入水条件下的优化结果进行数据分析.
为了对比本文提出的优化控制策略与其它控制策略的运行效果，本文仿真了以下几种不同的控制策略：
CS1： 文[10]所述的闭环控制： SO，5，ref(g·m-3)=2，SNO，2，ref=1，单位为(g·m-3)； Qint=55 338，Qw=385，单位为(m3·d-1).
CS2： 文[18]的研究结果： SO，5，ref=2，SNO，2，ref=2，SS5，ref=4 500，单位为(g·m-3)； r=1.5.
CS3： 采用所提出的IDE算法，优化周期不分段，得到的优化结果： SO，5，ref=0.68，SNO，2，ref=2，SS5，ref=5 000，单位为(g·m-3)； r=1.5.
CS4： 区分周内与周末两种时段，采用IDE算法得到的优化结果： 即周内的优化结果： SO，5，ref=1，SNO，2，ref=2，SS5，ref=5 000，单位为(g·m-3)； r=1.5； 周末的优化结果： SO，5，ref=0.5，SNO，2，ref=2，SS5，ref=4 833，单位为(g·m-3)； r=1.4.
表 2~4列出了上述4种不同控制策略下系统的运行代价(OC)、 污泥处理费用(SP)、 曝气能耗(AE)、 泵送能耗(PE)和排放出水所要缴纳的费用(EF)，污水处理过程关键出水水质变量中有4个变量在运行过程发生越限现象，表中也列出了这些变量越限时间占运行时间的百分比，即： ％Tviol.SNH，e，％Tviol.SSe，％Tviol.Ntot，e，％Tviol.CODe，其中关键出水水质变量的限制条件(见文[3])及我国对城镇污水处理厂污染物排放标准(GB 18918-2002)重点工程实现一级标准的B标准： SNH，e<4 g·m-3； Ntot，e<18 g·m-3； BODe<10 g·m-3； CODe<60 g·m-3； SSe<30 g·m-3.
| 性能 | CS1 | CS2 | CS3 | CS4 |
| OC /(＄·m-3) | 12 947 | 6 458 | 5 382 | 5 338 |
| SP /(kg·d-1) | 2 358 | 1 947 | 1 861 | 1 871 |
| AE /(kW·h·d-1) | 7 169 | 7 399 | 6 772 | 6 893 |
| PE /(kW·h·d-1) | 1 953 | 2 591 | 3 565 | 3 293 |
| EF /(kW·h·d-1) | 10 856 | 4 485 | 3 418 | 3 382 |
| ％Tviol.CODe | 1.2 | 2.2 | 2.7 | 2.7 |
| ％Tviol.Ntot，e | 10.9 | 0.1 | 0 | 0 |
| ％Tviol.SNH，e | 27.1 | 4.2 | 9.2 | 6.0 |
| ％Tviol.SSe | 0 | 1.0 | 1.5 | 1.3 |
| 性能 | CS1 | CS2 | CS3 | CS4 |
| OC /(＄·m-3) | 12 648 | 7 263 | 6 187 | 6 143 |
| SP /(kg·d-1) | 2 606 | 2 252 | 2 163 | 2 174 |
| AE /(kW·h·d-1) | 7 285 | 7 474 | 6 839 | 6 960 |
| PE /(kW·h·d-1) | 17 49 | 2 345 | 3 149 | 2 930 |
| EF /(kW·h·d-1) | 10 442 | 5 155 | 4 107 | 4 067 |
| ％Tviol.CODe | 2.7 | 4.0 | 4.3 | 4.3 |
| ％Tviol.Ntote | 15.0 | 0.6 | 0 | 0 |
| ％Tviol.SNHe | 26.8 | 4.6 | 12.6 | 7.6 |
| ％Tviol.SSe | 0.3 | 3.6 | 3.9 | 3.8 |
图 3画出了在不同的天气条件下，应用4种不同的控制策略，关键出水水质变量CODe、 BODe、 Ntot，e、 SNH，e、 SSe随时间的变化情况.
 |
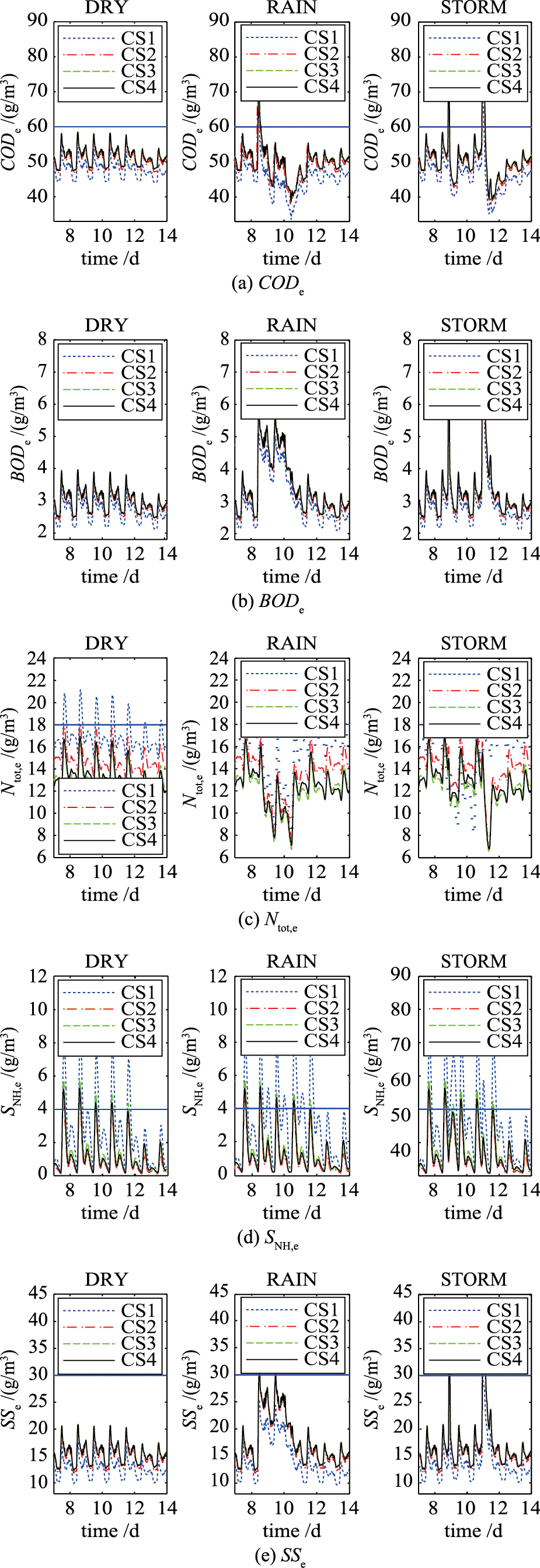| 图 3 不同天气条件下出水水质变化情况Fig. 3 Effluent variables under different weather conditions |
从表 2～4的运行结果可以看出，在3种不同天气入水条件下，CS4和CS3所起的作用在运行代价(OC)方面明显优于CS1和CS2，结果验证了采用IDE算法优化下的控制可以明显地提高污水处理过程的综合运行效率. 对比CS4和CS3，区分周内与周末两种时段的优化周期设定情况下，CS4所得的污泥处理费用(SP)和曝气能耗(AE)比CS3有所升高，然而以此为代价的泵送能耗(PE)、 排放出水所要缴纳的费用(EF)及出水水质变量越限时间长度相比CS3却有所降低，最终CS4可以得到更低的运行代价.
表 2～4的硝酸氮浓度SNH，e计算值表明了在不同控制策略实现不同天气条件入水的污水生化处理中，该项指标均出现了越限的情况. 这是因为在污水生化处理过程，即使采用最大的曝气量，也无法完全消除SNH，e，而且曝气能耗在污水生化处理过程的运行代价中占有很大的比例(约40％左右)[5]，因此，污水生化处理过程常常牺牲一定的SNH，e出水水质越限惩罚以达到更大的节约曝气能耗的目的.
图 3(a)和3(b)画出了出水水质变量CODe和BODe随时间的变化曲线，可知在不同的控制策略及不同的天气入水条件下，CS3和CS4两种控制策略作用均稍逊于CS1和CS2，却因此节省了更多运行代价.
图 3(c)画出了出水水质变量Ntot，e随时间的变化曲线，可知在CS1控制作用下在晴天、 雨天、 暴雨天条件下分别发生了7次、 5次、 5次的越限情况，而且每次越限均 维持了一定的时间. 而在CS2控制作用下，发了1、 2次的越限情况，越限持续时间较短. 采用本文所提出的IDE算法优化下的控制CS3和CS4，该变量均没有发生越限情况，并且CS3的效果稍优于CS4.
图 3(d)画出了出水水质变量SNH，e随时间的变化曲线，可知CS1控制作用下发生了多次的越限情况且维持了较长的时间. 其它3种控制策略下也发生了多次的越限情况，但是每次越限持续时间相比CS1短，且CS2控制效果稍优于CS3，CS3控制效果稍优于CS4.
图 3(e)画出了出水水质变量SSe随时间的变化曲线，可知4种控制策略作用下CS1的控制效果最好，因为在CS1中污泥排放量和内回流量为开环定量控制且维持在较低的控制作用下，而其它3种情况下的控制均随入水情况变化而变化，这样在CS1控制下，沉淀池的水力变化对污泥的沉降创造更有利的环境，所以可以获得更好的SSe. 对比其它3种控制策略(CS2、 CS3和CS4)中SSe的变化情况，CS2获得了稍好的效果.
4 结论污水生化处理是一个多变量的耦合非线性系统，在污水处理过程中，这些过程变量的取值不仅决定着污水处理出水水质的情况，更是影响着污水处理过程的各项运行代价，如曝气能耗、 泵送能耗、 污泥处理费用等. 针对如何确定污水生化处理过程被控变量的设定值取值问题，本文提出了一种改进的差分进化算法，并通过4个典型函数验证了所提出算法的寻优精度与收敛速度，然后采用了一个综合污水处理过程多方面性能指标的函数作为优化目标函数，在BSM1仿真平台上寻优计算了晴天入水条件下的污水生化处理过程被控变量设定值； 最后，通过对比4种不同控制策略对3种不同天气入水的污水处理结果，可知基于改进差分进化算法优化下的污水生化处理(CS4和CS3)相比其它的两种(CS1和CS2)控制策略明显可以降低系统的运行代价，缩短关键出水水质变量的越限时间长度，提高了出水水质. 其中CS4在仿真的4种情况中运行效果是最好的.
| [1] | Guerrero J, Guisasola A, Comas J, et al. Multi-criteria selection of optimum WWTP control setpoints based on microbiology-related failures, effluent quality and operating costs[J]. Chemical Engineering Journal, 2012, 188(1): 23-29. |
| [2] | Ruano M V, Ribes J, Sin G, et al. A systematic approach for fine-tuning of fuzzy controllers applied to WWTPs[J]. Environmental Modelling & Software, 2010, 25(5): 670-676. |
| [3] | Amand L, Carlsson B. Optimal aeration control in a nitrifying activated sludge process[J]. Water Research, 2012, 46(7): 2101-2110. |
| [4] | 张平, 苑明哲, 王宏. 前置硝化污水生化处理过程优化控制[J]. 信息与控制, 2008, 37(1): 112-118. Zhang P, Yuan M Z, Wang H. Optimization control for pre-denitrification type of biological treatment process for wastewater[J]. Information and Control, 2008, 37(1): 112-118. |
| [5] | 林梅金, 罗飞, 许玉格. 基于蛙跳粒子群算法的污水生化处理优化控制[J]. 华南理工大学学报: 自然科学版, 2013, 41(9): 51-57. Lin M J, Luo F, Xu Y G. Optimal control of wastewater biological treatment process based on a hybrid optimization method of SFLA and PSO[J]. Journal of South China University of Technology: Natural Science Edition, 2013, 41(9): 51-57. |
| [6] | 史雄伟, 乔俊飞, 苑明哲. 基于改进粒子群优化算法的污水处理过程优化控制[J]. 信息与控制, 2011, 40(5): 698-703. Shi X W, Qiao J F, Yuan M Z. Optimal control for wastewater treatment process based on improved particle swarm optimization algorithm[J]. Information and Control, 2011, 40(5): 698-703. |
| [7] | Vanrolleghem P A, Gillot S. Robustness and economic measures as control benchmark performance criteria[J]. Water Science & Technology, 2002, 45(4/5): 117-126. |
| [8] | Guerrero J, Guisasola A, Vilanova R, et al. Improving the performance of a WWTP control system by model-based setpoint optimisation[J]. Environmental Modelling & Software, 2011, 26(4): 492-497. |
| [9] | 崔文华, 刘晓冰, 王伟, 等. 混合蛙跳算法研究综述[J]. 控制与决策, 2012, 27(4): 481-486. Cui W H, Liu X B, Wang W, et al. Survey on shuffled frog leaping algorithm[J]. Control and Decision, 2012, 27(4): 481-486. |
| [10] | Union E, Direction G D L R. The COST simulation benchmark: Description and simulator manual[M]. Brussels, Belgium: Directorate-General for Research and Innovation, 2002. |
| [11] | Storn R, Price K. Differential evolution-A simple and efficient heuristics for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. |
| [12] | 辛斌, 陈杰. 粒子群优化与差分进化混合算法的综述与分类[J]. 系统科学与数学, 2012, 31(9): 1130-1150. Xin B, Chen J. Particle swarm optimization and differiential evolution: State of the art[J]. Journal of Systems Science and Mathematical Sciences, 2012, 31(9): 1130-1150. |
| [13] | Kim P, Lee J. An integrated method of particle swarm optimization and differential evolution[J]. Journal of Mechanical Science and Technology, 2009, 23(2): 426-434. |
| [14] | Zhang C S, Ning J X, Lu S, et al. A novel hybrid differential evolution and particle swarm optimization algorithm for unconstrained optimization[J]. Operations Research Letters, 2009, 37(2): 117-122. |
| [15] | 张春美, 陈杰, 辛斌. 武器目标分配问题的离散差分进化算法[J]. 北京理工大学学报, 2014, 34(3): 289-293. Zhang C M, Chen J, Xin B. A discrete differential evolution algorithm for the weapon target assignment problem[J]. Transactions of Beijing Institute of Technology, 2014, 34(3): 289-293. |
| [16] | Kaelo P, Ali M M. A numerical study of some modified differential evolution algorithms[J]. European Journal of Operational Research, 2006, 169(3): 117621184. |
| [17] | Qin A K, Huang V L, Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. |
| [18] | Vreko D, Hvala N, Kocijan J. Wastewater treatment benchmark: What can be achieved with simple control?[J]. Water Science & Technology, 2002, 45(4/5): 127-134. |