2. 广州中国科学院沈阳自动化研究所分所, 广东 广州 511458;
3. 中国科学院大学, 北京 100049
2. Shenyang Institute of Automation, Guangzhou, Chinese Academy of Sciences, Guangzhou 511458, China;
3. University of the Chinese Academy of Sciences, Beijing 100049, China
1 引言
随着信息化技术的不断发展,人们对定位技术的需求日益增长. 其中,室内定位技术越来越多地在车间、 商场、 车站、 机场等生产场所或公共场所内使用. 根据定位过程中是否需要测量已知点与未知点之间的距离,可以将室内定位方法分为两大类,即基于测距的方法(range-based localization scheme)和无需测距的方法(range-free localization scheme)[1, 2]. 基于测距的定位方法是通过测量节点间的距离或角度信息,使用三角形质心、 三边测量、 最小二乘法或最大似然估计等方法估算节点的位置,目前比较常用的测距技术有TOA(time of arrival)、 TDOA(time difference of arrival)、 AOA(angel of arrival)和RSSI(received signal strength indication)等[3, 4, 5]; 无需测距的定位方法则无需测量节点间的距离或角度信息,仅根据网络连通性等信息即可完成节点的位置估算,常用的方法包括: 质心算法、 Amorphous算法、 DV-Hop算法、 APIT算法、 蒙特卡洛定位算法等[6, 7, 8]. 与TOA、 TDOA、 AOA等测距定位方法相比,RSSI测距定位方法不需要额外的硬件开销即可获取RSSI值,再经数据处理及算法便能实现定位. 因而,基于RSSI测距的定位技术正逐渐成为室内定位技术的研究热点之一.
目前,RSSI定位算法的应用主要有3种模式: 一种是需要预先测试环境信息,获取相应的定位参数,并采用修改参数值作为实际定位的参数[9]; 另一种是预先测试环境,对定位区域作大量的RSSI值测试,并保存测试的RSSI值数据库,建成RSSI-Map,供实际使用时查询调用[10]; 第3种是无需预先测试环境信息的方法,直接在定位区域布置节点进行定位,采用迭代分布式算法、 双曲线模型算法、 HCRL(Hop-Count-Ratio based Localization)[11, 12]算法等直接进行定位计算. 室内环境的特殊性使得无线信号在室内传输时存在反射、 绕射、 折射和散射等现象,导致发射端信号存在多条路径到达接收端,从而产生多径衰落效应,造成接收端RSSI大幅波动,给测距带来较大误差. 因而,对如何提高RSSI测距精度的研究是十分必要且有意义的. 文[13]认为根据较大的RSSI值估算出的距离值相对接近真实值,因而提出了一种对RSSI值进行加权的算法; 文[14]中提出了一种利用RSSI指纹匹配的方法来进行室内定位的方法,该方法的定位精度在很大程度上依赖于RSSI指纹的采集,工作量大; 文[15, 16]中提出了将最大似然估计引入“常数—对数”模型进行定位的方法,与传统的“常数—对数”模型相比,该方法在一定程度上可提高定位精度,但仍难以满足需求; 而文[17]的研究表明,在节点移动的情况下,节点的RSSI波动较大,仅将RSSI测距值作为定位的唯一依据,结果并不可靠. 可以看出,利用RSSI进行测距定位受到影响因素很多,具有明显的不确定性.
本文定量地分析了信号受环境的影响过程中各因素所起的作用,通过实测得出信号强度随信道和传播距离之间的关系. 根据实验的结果,设计了多个不同频率的信号强度平均值作为等效信号强度,进行测距计算,并应用在基于RSSI的定位方法中. 实验结果表明,使用多信道信号强度进行的定位,能有效提高定位的精度.
2 实验设计 2.1 实验环境为了分析室内环境下多径传播对信号强度的影响,本文设计了以下实验系统:
实验装置方面,采用3组无线传感网节点建立实验平台. 传感网分别使用433 MHz,470 MHz,2.4 GHz频率. 每个传感网节点都能记录收到报文时的实时信号强度. 实验环境方面,选择了典型室内走廊环境进行测试. 实验场地如图 1所示. 发送节点和接收节点均采用三脚架固定,离地高度为0.6 m,并保持天线垂直于地面. 发送端和接收端为直视链路.
 |
| 图 1 实验场地Fig. 1 The experimental environment |
实验时将固定点放置在场地一侧,移动点分别在一条直线上多个固定距离进行多个信道的RSSI读取,每个位置间距为20 cm,每1 s测试一次信号强度值,每个位置每个信道测试100次. 在测试过程中,每次测量完成之后更换一个测试信道,3个频段上分别使用10、 10、 16个信道.
2.2 实验结果经过实地的测试,实验结果如图 2所示.
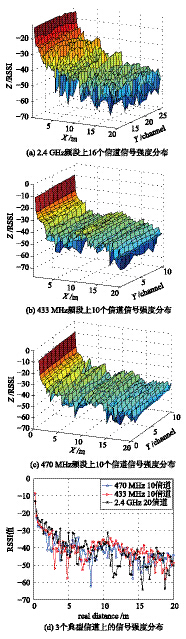 |
| 图 2 不同信道不同位置信号强度分布Fig. 2 The signal strength distribution in different channels and locations |
根据实验结果可以看出,在室内环境中,不同的信道情况下,同样的发送和接收方,所测得的信号强度不同. 大部分信道上的叠加信号强度相近,但个别信道上叠加信号强度明显偏离中间水平. 以2.4 GHz频段为例,在16个信道中,可能会在多个信道出现较强的信号强度,而这些出现较强的信号强度的信道也不是相邻的. 这是因为16个信道的中心频率的变化不是连续的,其不同的频率值,造成的信号叠加的效果也不是连续的. 同一频段由于信道频率差距较小,RSSI波动的趋势基本相同,没有区分度; 2.4 GHz、 433 MHZ和470 MHz频段由于频率差距明显,相同位置测得的RSSI结果差距较大.
在单个信道下测量的RSSI值随距离的变化很大,从整体趋势上看符合“常数—对数”模型[18]. 在0~5 m范围内,信号波动不明显,在5 m~20 m处,信号波动明显.
3 信号强度变化原理分析大量研究表明,无线信号空间传播的路径衰减遵循“常数—对数”模型:
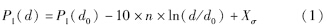
RSSI测距是基于发射节点和接收节点之间距离d与无线传播路径损耗之间的关系来实现的. 式(1)中Pl(d)在不考虑多径效应的情况下,有:
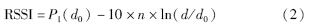
从式(2)可以看出,在理想情况下,信号强度值同距离之间关系应该是一个平滑的曲线.
然而实验结果却是一条波动很大的曲线,与理论值不符. 根据情况比对,实际测量情况由于是在室内,受地面反射影响较大,因此,可考虑是由于多径反射造成的影响.
为了验证这个猜想,本文设计了一个简单的地面反射场景.
无线信号传播之后可以表示为
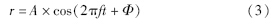
在实际问题中,反射物不可能做到对无线电波的无损耗反射,实际的情况是在一个区域内,无线信号将会受到地面、 墙体、 障碍物等多种情况下的反射传播. 因此,实际的信号叠加模型将变为
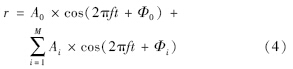
为了更直观地说明问题,本文对最简单的情况进行分析.假设测距发生在只有地面反射的一个开放空间内,地面为理想介质,经地面反射的信号同入射信号强度相同,如图 3所示.
 |
| 图 3 地面反射模型Fig. 3 Ground reflection model |
假设发射点距地面距离为h,发射点和接收点的距离为l,则可得一次反射情况下接收点的信号叠加强度为
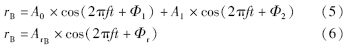
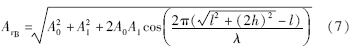
根据无线电波空间传播规律,幅值Ai同传输距离成反比关系,因此:
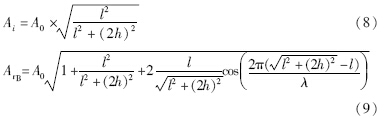
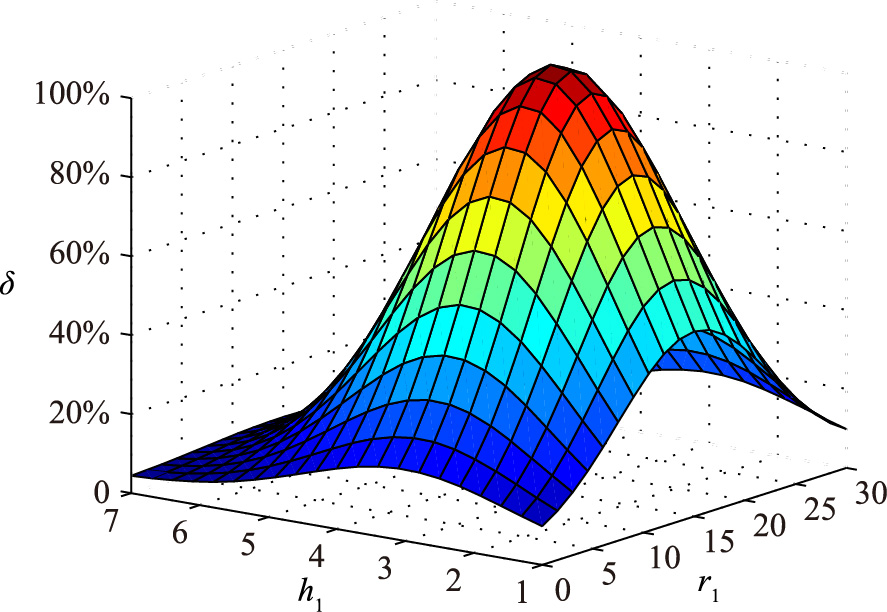
根据式(9)可知,无论是发射端和接收端之间的距离l,发射点到地面的高度h,发射端和接收端所处的反射环境,还是射频信号的波长λ,其不同的取值都会影响到叠加之后波形的幅值. 这就解释了2.2节实验的结果.
推广到实际情况中,多个反射面以及有衰减的反射,将不会对信号强度的变化趋势有质的影响.
4 多信道定位方法 4.1 定位流程通过上文的分析,本文综合考虑了实现性和性能,提出了使用多个信道的RSSI值进行定位的方法. 具体执行步骤如下:
Step 1: 标定阶段,在固定点测量多个信道RSSI值,记录并计算定位参数.
Step 2: 系统准备,部署定位锚节点,实现目标节点和锚节点的同步.
Step 3: 在目标节点上分别使用多个信道进行通信.
Step 4: 信号处理阶段,将RSSI处理成信号强度幅值,并计算距离理论值.
Step 5: 定位阶段,在定位服务器上根据各个信号强度计算位置.
4.2 多信道测距的适用范围根据上节式(9)可分析,叠加后的信号幅值ArB应在A0上下波动. 这时存在3种情况:
1) 当l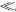 h时,叠加后的信号幅值ArB接近于直线传播的信号强度A0.
h时,叠加后的信号幅值ArB接近于直线传播的信号强度A0.
2) 当l同h数量级接近且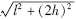 -l大于或接近λ时,ArB的范围应在
-l大于或接近λ时,ArB的范围应在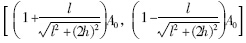 之间,即范围在0~2倍直线传播的信号强度A0之间.
之间,即范围在0~2倍直线传播的信号强度A0之间.
3) 当l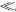 h且
h且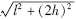 -l远小于λ时,叠加后的信号强度应接近于
-l远小于λ时,叠加后的信号强度应接近于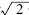 倍的直线传播信号强度A0.
倍的直线传播信号强度A0.
根据实际硬件RSSI寄存器的最小标度情况,当距离大于30m之后,RSSI的变化极其缓慢,信号传播数米或数十米之后信号强度才变化一个单位,因此,室内定位的范围一般在1 m~15 m之内,否则精度将大大降低. 因此,在定位应用中,信号强度的变化规律将符合上文中的前两种情况.
当l和h都固定的时候,为了使ArB能够在A0附近波动并取到0~2倍A0的全部值,则要求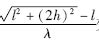 变化范围要超过1,即1个余弦周期. 当频段在400 MHz到2.485 GHz范围内变化时,则要求高度h最少为1.06 m. 当h越大时,l越小时,其覆盖半个余弦周期所需要的频段就越小. 在最大15 m范围内,当h大于5 m的情况下仅2.4 GHz频段(2.4~2.485 GHz)可在同一位置取到信号强度的全部值.
变化范围要超过1,即1个余弦周期. 当频段在400 MHz到2.485 GHz范围内变化时,则要求高度h最少为1.06 m. 当h越大时,l越小时,其覆盖半个余弦周期所需要的频段就越小. 在最大15 m范围内,当h大于5 m的情况下仅2.4 GHz频段(2.4~2.485 GHz)可在同一位置取到信号强度的全部值.
根据前文介绍,式(2)中Pr(d0)为距离发射点1 m处的RSSI值,可视为常量,本文记作B,则:
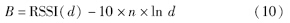
由式(10)可得,常数B及n的值决定了发射点和接收点之间距离d与接收信号强度之间的关系. 通过实测不同的d位置的RSSI值,即可使用曲线拟合方法拟合出这两个数值. 有了这两个数值,在获得RSSI值之后,可利用式(10)计算出某一个接收位置到发射端的距离[19]:

由式(11)可知,用来进行测距计算的RSSI值越接近于直线传播的RSSI值,计算出来的距离就越准确.
4.4 多信道距离估算根据4.2节的结论,当频率范围足够大的时候,信号可以覆盖到取值的最大值和最小值. 因此,可设计在多个信道获取信号强度值进行测距和定位.
首先需要将测量得到的RSSI值转换为信号幅值,根据信号幅值的平方同功率成正比,有:

RSSI值与功率的关系式为



由于并非是1阶方程组,因此不能直接使用最小二乘法求解A0的近似值. 而定位发生在单片机上,因此也不适合用其它复杂方法进行求解.
为了求解A0的近似值,可使用特解的方式来完成. 在式(15)中,当ArB分别取最大和最小值时有:
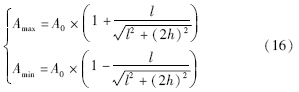
因此,可近似计算信号幅值的中心值:

在获得了幅度中心值之后,通过式(14)反推得到RSSI值,代入到式(11)中即可计算出距离.
4.5 MinMax定位方法根据Luo等[20]的研究结果,MinMax法在室内定位中精度较高,计算复杂度也较低,因此,本文选用该方法作为定位方法.
在MinMax算法中,每个锚节点测量来自所述目标节点的RSSI值,并根据该值计算它到目标节点之间的距离d,然后以该锚节点为中心,绘制宽度为2d的正方形.最终认为目标节点处在所有锚节点绘制的正方形的重叠区域内,如图 4所示.
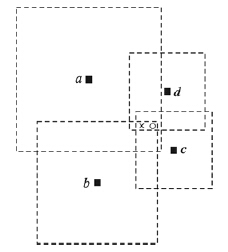 |
| 图 4 MinMax定位方法Fig. 4 MinMax positioning method |
图 4是MinMax算法的原理示意,其中圆圈表示目标节点,实心方块表示锚节点,交叉则表示估计位置.
MinMax算法坐标计算方法如下:
以锚节点a为例,a的坐标为(xa,ya),在a点接收到的RSSI值计算距离未知节点的估计距离为da,以2×da为边长,(xa,ya)为中心画正方形,则正方形的4个顶点的坐标为
(xa-da,ya-da),(xa-da,ya+da)
(xa+da,ya+da),(xa+da,ya-da)
在本文简单表示为(xa-da,ya-da)×(xa+da,ya+da)
以此类推,其余锚节点的顶点坐标为
(xi-di,yi-di)×(xi+di,yi+di)
最终正方形重叠区域的4个顶点坐标为
[max(xi-di),max(yi-di)]×
[min(xi-di),min(yi-di)]
则,估计的目标节点的位置是重叠区域的中心位置,其坐标可以根据4个顶点坐标计算:[(max(xi-di)+min(xi+di))/2,
(max(yi-di)+min(yi+di))/2]
5 实验和结果 5.1 实验参数设置为了全面论证本方法的可行性,在长度为15 m、 宽度为15 m的室内场地进行了实验,实验场地如图 5所示. 移动节点和固定节点均采用三脚架固定,离地高度为1.5 m,并保持天线垂直于地面. 环境中存在少量植物、 桌椅等遮挡物,测试过程中有人员走动.
 |
| 图 5 室内定位环境和定位节点Fig. 5 Indoor positioning environment and positioning node |
为了验证多信道的精度,使用每个频段各1个信道进行RSSI测量,记录测量结果,用3个频段上测得的RSSI值进行计算,同时每个频段上各选了一个信道进行计算,并将计算结果进行对比. 选择10个位置进行测量.
使用的目标定位设备仍是2.1节中的3个设备,同锚节点间并未进行同步.
本文用到的实验参数如表 1所示.
| 参数 | 数值 |
|
锚节点距离l (单位: m) | 15 |
| 锚节点个数 | 4 |
| 锚节点坐标 | (0,-7.5),(15,-7.5) (15,7.5),(0,7.5) |
| 使用的信道频率 (单位: Hz) | 2.4 G(16个信道)、 433 M(10个信道)、 470 M(10个信道) |
| 对比信道频率 (单位: Hz) | 443 M、 480 M、 2.450 G |
| 测试场地规格 (单位: m) | 15×15 |
| 测试设备离地高度 (单位: m) | 1.5 |
| 测试点坐标 | (2,2),(4,-1),(7,-4),(10,-3), (12,0),(14,4),(9,3),(11,6), (5,6),(13,-5) |
B、 n值分别采用单个信道和多个信道的实测RSSI值进行计算,得到的值如表 2所示.
| B | n | |
| 3个频段平均值 | -28 | 1.6 |
| 443 MHz信道 | -32 | 1.2 |
| 480 MHz信道 | -30 | 1.4 |
| 2.450 GHz信道 | -27 | 1.7 |
通过B,n值计算得出的定位结果如图 6所示.平均误差曲线图如图 7所示.
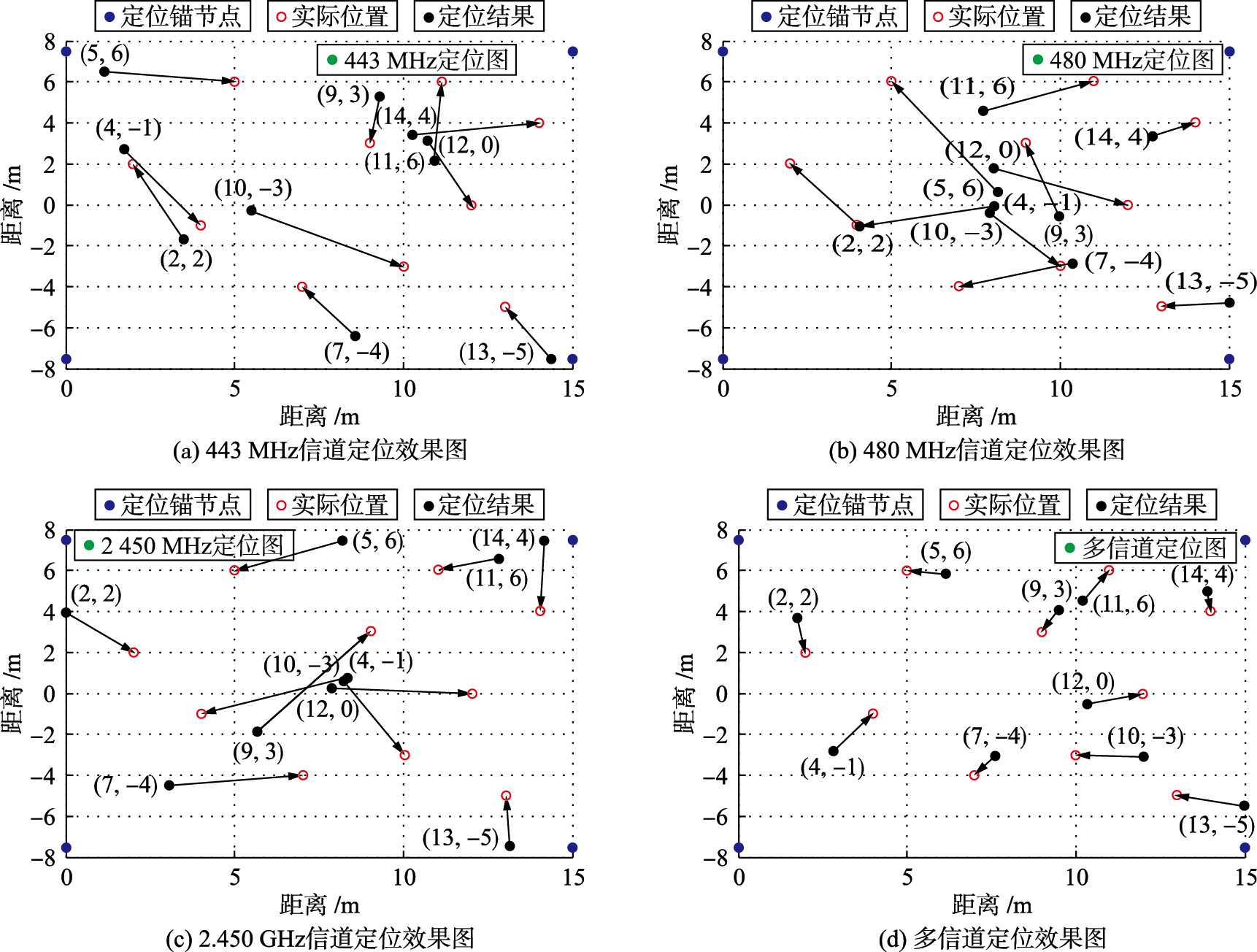 |
| 图 6 定位结果Fig. 6 Localization results |
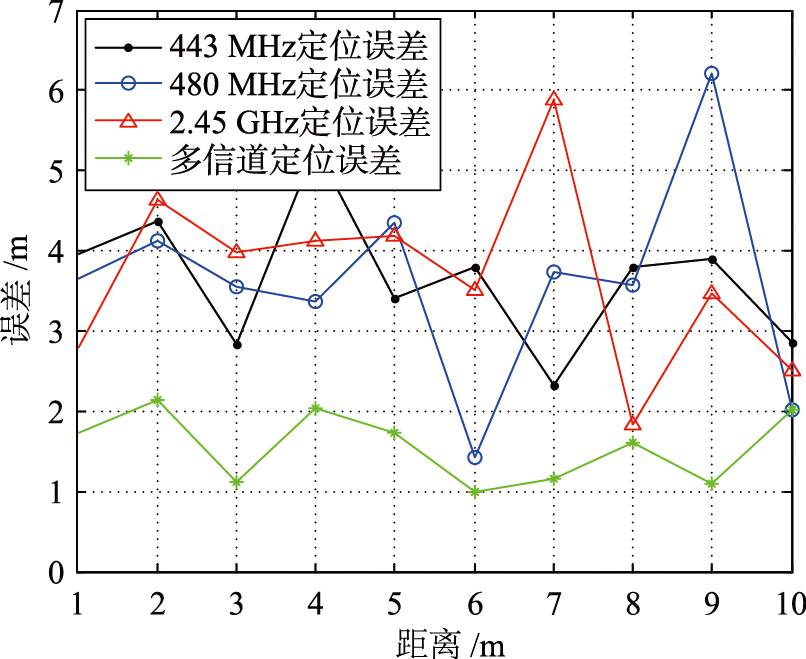 |
| 图 7 定位误差Fig. 7 Localization errors |
由图 7可以看出,使用多信道处理方法进行定位的误差远小于使用单个信道进行定位的误差. 个别的误差较大的情况,是因为多信道数据在处理方法上只使用了最大值和最小值,但由于实验中使用的频率分布不均匀且不连续,因此有可能取不到极值点,所以存在误差. 如果频率能分布的更加均匀,则定位精度将更高. 5.2.2 系统开销分析
根据实验的处理过程可知,最后使用数据仅仅是测量到的信号强度值的最大值和最小值. 因此,在能保证使用的频段覆盖到极值的情况下,可以减少需要测量信号强度的信道数,以降低系统开销.
6 结论本文通过对多信道的RSSI值进行理论分析和物理实验,研究了室内环境对于无线信号传播的信号强度的影响规律. 根据此规律,提出了基于多信道数据的测距定位方法,提高测距定位精度. 通过使用3个频段上的多个信道进行定位实验,验证了本文提出的设想的可行性.
下一步,将考虑分析多信道的选取规律,通过使用最少的信道数达到提高定位精度的目的. 此外,还将考虑利用跳频技术来消除系统所受到的干扰,减少定位过程中的报文重传数目,提高定位的速度和效率.
| [1] | He X, Xiao Y, Wang Y. A LSSVR three-dimensional WSN nodes location algorithm based on RSSI[C]//2011 International Conference on Electrical and Control Engineering. Piscataway, NJ, USA: IEEE, 2011: 1889-1895. |
| [2] | Wang J Y, Chen C P, Lin T S, et al. High-precision RSSI-based indoor localization using a transmission power adjustment strategy for wireless sensor networks[C]//2012 IEEE 14th International Conference on High Performance Computing and Communication & 2012 IEEE 9th International Conference on Embedded Software and Systems. Piscataway, NJ, USA: IEEE, 2012: 1634-1638. |
| [3] | 高国胜, 陈俊杰, 李刚. 基于RSSI测距的信标节点自校正定位算法[J]. 测控技术, 2009, 28(8): 93-97. Gao G S, Chen J J, Li G. Beacon node self-tuning localization algorithm based on RSSI[J]. Measurement & Control Technology, 2009, 28(8): 93-97. |
| [4] | Wang J, Ghosh R K, Das S K. A survey on sensor localization[J]. Journal of Control Theory and Applications, 2010, 8(1): 2-11. |
| [5] | Pal A. Localization algorithms in wireless sensor networks: Current approaches and future challenges[J]. Network Protocols and Algorithms, 2010, 2(1): 45-73. |
| [6] | Kuriakose J, Joshi S, Raju R V, et al. A review on localization in wireless sensor networks[M]//Advances in Signal Processing and Intelligent Recognition Systems. Berlin, Germany: Springer, 2014: 599-610. |
| [7] | 刘颖, 苏俊峰, 朱明强. 基于迭代容积粒子滤波的蒙特卡洛定位算法[J]. 信息与控制, 2013, 42(5): 632-638. Liu Y, Su J F, Zhu M Q. A Monte-Carlo localization algorithm based on iterated cubature particle filter[J]. Information and Control, 2013, 42(5): 632-638. |
| [8] | Zhang J, Wu Y H, Shi F, et al. Localization algorithm based on DV-HOP for wireless sensor networks[J]. Journal of Computer Applications, 2010, 30(2): 323-326. |
| [9] | Priwgharm R, Srivilas K, Cherntanomwong P. Indoor localization system using RSSI measurement in wireless sensor networks based on ZigBee standard[C]//The 3rd National Conference on Information Technology. Piscataway, NJ, USA: IEEE, 2010: 225-228. |
| [10] | Anzai D, Hara S. An RSSI-based MAP localization method with channel parameters estimation in wireless sensor networks[C]//Proceedirgs of the 69th IEEE Conference on Vehicular Technology. Piscataway, NJ, USA: IEEE, 2009: 1-5. |
| [11] | Yang S, Yi J, Cha H. HCRL: A hop-count-ratio based localization in wireless sensor networks[C]//4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks. Piscataway, NJ, USA: IEEE, 2007: 31-40. |
| [12] | Ma D, Er M J, Wang B, et al. Range-free wireless sensor networks localization based on hop-count quantization[J]. Telecommunication Systems, 2012, 50(3): 199-213. |
| [13] | Gao L, Zhu M, Yang D. Simulation and implement of weighted centroid localization algorithm based on ZigBee[J]. Chinese Journal of Sensors and Actuators, 2010, 23(1): 30-32. |
| [14] | Priwgharm R, Chemtanomwong P. A comparative study on indoor localization based on RSSI measurement in wireless sensor network[C]//2011 Eighth International Joint Conference on Computer Science and Software Engineering. Piscataway, NJ, USA: IEEE, 2011: 1-6. |
| [15] | Dieng N A, Charbit M, Chaudet C, et al. A multi-path data exclusion model for RSSI-based indoor localization[C]//2012 15th International Symposium on Wireless Personal Multimedia Communications. Piscataway, NJ, USA: IEEE, 2012: 336-340. |
| [16] | 任维政, 徐连明, 邹德君, 等. 基于RSSI差分似然估计的WSN节点定位算法[J]. 数据采集与处理, 2009(6): 757-761. Ren W Z, Xu L M, Zou D J, et al. Positioning algorithm using maximum likelihood estimation of RSSI difference in wireless sensor networks[J]. Journal of Data Acquisition and Processing, 2009(6): 757-761. |
| [17] | Dong Q, Dargie W. Evaluation of the reliability of RSSI for indoor localization[C]//2012 International Conference on Wireless Communications in Unusual and Confined Areas. Piscataway, NJ, USA: IEEE, 2012: 1-6. |
| [18] | 沈军, 黄春华, 罗护, 等. 基于RSSI优化的模型参数实时估计定位算法[J]. 计算机工程与设计, 2012, 33(2): 464-468. Shen J, Huang C H, Luo H, et al. Localization algorithm of model parameters real-time estimate based on RSSI optimized[J]. Computer Engineering and Design, 2012, 33(2): 464-468. |
| [19] | 章坚武, 张璐, 应瑛, 等. 基于ZigBee的RSSI测距研究[J]. 传感技术学报, 2009, 22(2): 285-288. Zhang J W, Zhang L, Ying Y, et al. Research on distance measurement based on RSSI of ZigBee[J]. Chinese Journal of Sensors and Actuators, 2009, 22(2): 285-288. |
| [20] | Luo X, O'brien W J, Julien C L. Comparative evaluation of Received Signal-Strength Index (RSSI) based indoor localization techniques for construction jobsites[J]. Advanced Engineering Informatics, 2011, 25(2): 355-363. |



