1 引言
随着社会经济发展,传统能源已远远不能满足需求,风能凭借其取之不尽用之不竭的优势,成为新能源开发的首选对象.
传动系统是风能转换控制系统的执行器,而齿轮箱又是传动系统中最重要的部件.由于风能转换机组多安装在沿海、高原等复杂多变的恶劣工作环境中,长期处于大功率、 高负荷的连续运行状态[1],齿轮箱承受着无规律的变向载荷的风力作用及强阵风冲击的变载荷作用,加上本身体积大、 结构复杂[2],齿轮箱的齿轮、 轴承等部件受长期老化、 冲击及干扰等因素的影响,传动系统经常发生一些非致命性的部分失效故障,如齿面的磨损(10%)、 划痕(10%)、 点蚀(31%)、 齿面疲劳及轴承形变等[3]. 这些故障严重影响系统的性能,造成机械转矩输出信号偏离准确值,体现了执行器部分失效的连续增益故障信息. 若不及时处理,会引起生产过程停顿,甚至可能造成严重灾难. 因此,研究风能转换系统的容错控制,保障系统在执行器部分失效故障时仍能维持在一定的性能范围之内继续稳定运行,同时为后期维护争取时间,是近年来提高风能转换系统可靠性的有效手段,并日益受到国内外学者广泛的关注[4, 5, 6, 7, 8, 9].
风能转换系统数学模型复杂,具有高阶、多变量、强耦合等特点,且受外部干扰严重,近年来各种控制方法被引入风能转换系统中[10, 11, 12, 13, 14, 15, 16]. 通过对风能转换系统模型进行线性化处理,实现其鲁棒控制. 文[10]在系统期望的稳态工作点附近对系统进行线性化处理,得到线性时不变系统状态方程. 然而由于风速的强不确定性,系统期望的稳态工作点也会随之发生变化,使得线性化模型的精度受到影响. 因此,有学者提出了系统线性变参数(linear parameter varying,LPV)模型[11],系统矩阵随参数变化而变化,模型的精度得到了明显提高,但是基于系统线性变参数模型的增益调度控制需要求解大量的线性矩阵不等式(linear matrix inequality,LMI),计算工作量庞大. T-S(Takagi-Sugeno)模糊模型[12]出现后,可以通过设计T-S线性子系统的控制器解决非线性控制问题,文[13]针对变速恒频风能转换系统参数不确定性和传感器故障,提出了一种多观测器转换控制的模糊鲁棒主动容错控制策略. 采用风能转换系统的参数不确定性T-S模糊模型,建立了传感器故障模型,同时建立模糊状态观测器,通过泰勒级数以及线性矩阵不等式(LMI)得到系统稳定的充分条件. 文[14]针对风能转换系统执行器故障问题,分析了风能转换系统的状态方程,将风能转换系统中执行器连续增益故障转化成传动系统参数的不确定性,建立风能转换系统的T-S模糊模型. 采用状态反馈并行分布补偿结构,设计了风能转换系统执行器发生故障时的鲁棒容错控制器,减缓了故障恶化的程度,提高了机组利用率. 但在实际控制系统的设计中,为实现对非线性系统良好的逼近特性,模糊模型往往需要数量庞大的模糊规则,尤其是在前件变量较多时,甚至会出现“规则爆炸现象”. 神经网络具有很强的非线性映射、 并行处理和自学习能力,并能对非线性系统以任意精度逼近,在非线性系统控制设计中具有独特的优势[15, 16].
本文采用RBF自适应神经网络在线对风能转换系统(WECS)执行器故障进行重构.未发生故障时,系统在正常模式下运行;故障发生时,根据故障的重构值设计滑模容错控制器的切换增益,进行在线控制律重构,并通过构造李亚普诺夫函数证明系统的鲁棒性和稳定性.仿真实验结果表明,在执行器发生故障时,滑模容错控制器下的系统,仍能够实现最大风能捕获,稳定运行,避免了系统进一步恶化,为配合下一步故障维修提供了宝贵的时间.
2 双馈风能转换系统建模忽略模型中的一些动态特性[17],建立双馈风能转换系统模型,结构图如图 1所示,主要包括风速模型、 空气动力学模型、 驱动链模型、 塔架模型、 变桨系统及发电机控制系统等. 风机捕获风能并转换成机械能,通过驱动链带动发电机转子旋转,由发电机将机械能转换为电能,经过转换器整流逆变后转换为符合要求的交流电输送到电网.
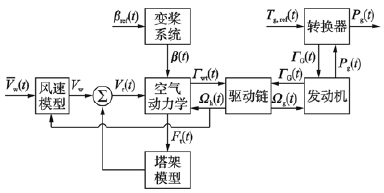 |
| 图 1 风能转换系统基本框图Fig. 1 Basic structure of wind energy conversation system |
根据贝兹理论,风机产生的机械功率[18]为
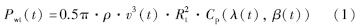
风机产生的风力矩为
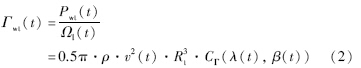
在额定风速以下时,调节发电机的电磁转矩跟随风速变化,使Cp(λ(t),β(t))达到最大值,实现风能的最大捕获. 在额定风速以下时,β(t)=0则Cp(λ(t),β(t))=Cp(λ(t)).
系统的高速轴运动方程如式(3)所示[19]:

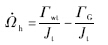
考虑发电机电磁转矩的惯性:

结合式(3)、 (4),风能转换系统动态状态方程表示为
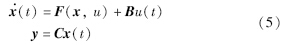
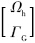 ,
u(t)=Γ*ref,F(x,u)
=
,
u(t)=Γ*ref,F(x,u)
=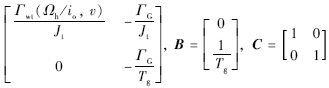 ;Γwt表示风力矩;Γ*ref表示电磁转矩的参考值;Ωh表示发电机转子转速;Jt表示高速轴端的转动惯量,值为Jwt/i2o;Jwt表示风轮机转轴的转动惯量.
;Γwt表示风力矩;Γ*ref表示电磁转矩的参考值;Ωh表示发电机转子转速;Jt表示高速轴端的转动惯量,值为Jwt/i2o;Jwt表示风轮机转轴的转动惯量. 从风能转换系统状态方程(5)可知系统的控制输入为参考的电磁转矩Γ*ref,即为驱动链执行侧的输出.
3 基于RBF神经网络执行器在线故障重构 3.1 RBF自适应故障观测器设计考虑执行器故障时,风能转换系统状态方程(5)可写作:
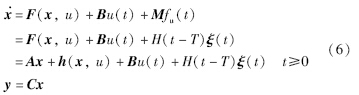
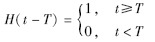
为了进一步分析,作如下假设:
假设1 故障发生后,系统的状态保持有界,即x(t)∈L∞.
假设2 矩阵A是满秩的,即rank(A)=n
假设3 A满足A、 C是可观的.
构建两个RBF神经网络分别逼近系统非线性项h(x,u)和故障ξ(t):
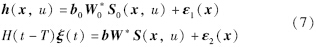
将式(7)代入(6)得
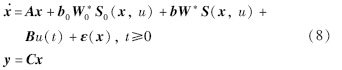
在实际风能转换系统,系统状态是不可测量的,为了估计系统的状态,构造观测器:
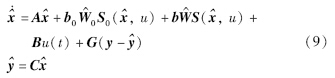
RBF神经网络对系统非线性部分逼近b0W^0S0(,u),RBF神经网络对故障逼近bW^S(,u),W^0为W*0的估计矩阵,W^为W*的估计矩阵,选择G使得A1=A-GC为稳定矩阵,且满足李亚普诺夫方程AT1P+PA1=-Q,P=PT>0,Q>0,通过上述观测器对风能转换系统实现系统状态的观测和故障估计.
令e=xˆ-x,由式(8)、 (9)可得到误差方程:
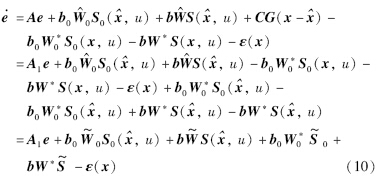
根据李亚普诺夫稳定方法,可以得出如下网络权重调整的算法:
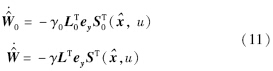
不考虑非线性系统(8)、 状态观测器(9)和误差方程(10),设存在一个充分大的集合Αd,使得系统满足假设1~3,则根据RBF神经网络权值在线更新率(11),误差e是最终一致有界,x^可作为x的估计.
证明 取李亚普诺夫函数:
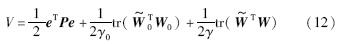
对V求导并结合误差方程(10),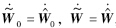 ,得
,得
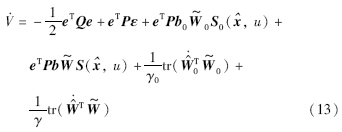
将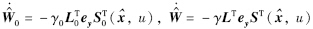 代入式(13),同时利用Pb0=CTL0,Pb=CTL,ey=y-y^=Ce,得
代入式(13),同时利用Pb0=CTL0,Pb=CTL,ey=y-y^=Ce,得
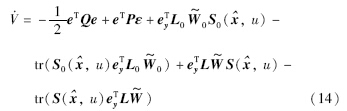
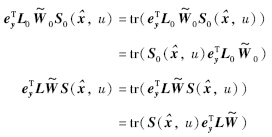
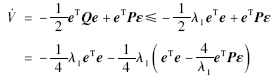
又
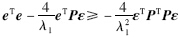

显然,当e≥2λ2λ1ε时,V·≤0,因而e∈L∞,系统具有鲁棒性.
风能转换系统非线性部分和系统发生的故障分别用RBF神经网络逼近,针对系统状态量不可测问题,根据式(9)构造观测器进行状态估计,根据估计状态,通过式(11)完成神经网络权重调整,进而由式(7)得到系统非线性项和故障估计. 显然,所有参数调整律都只用了可测输出和状态观测的信息. 重构的故障值为接下来滑模容错控制器切换增益设计提供依据.
4 滑模容错控制器
由式(5)得,状态变量x=[Ωh ΓG],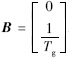 ,Mfu=H(t-T)ξ(t)为系统执行器故障.
,Mfu=H(t-T)ξ(t)为系统执行器故障.
在理想的情况下,系统进入滑动模后,满足σ=0,σ.=0,系统运动到此切换面上满足下列方程:
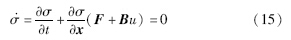
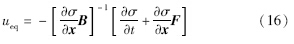
假定滑模动态过程(即在滑模面上)与模型等效:
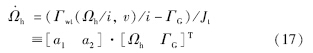
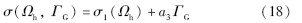
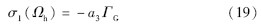
由式(18)可以得:
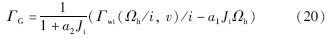
为了简便起见,令a3=1+a2Jt. 由式(16)~(18)共同推导的滑模面初始形式为
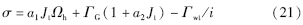
将式(21)代入式(16),得等效控制输入的表达式为
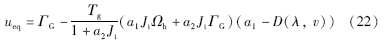
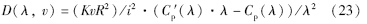
给出滑模控制律:


考虑实际情况中的抖动问题,用饱和函数改进切换项为
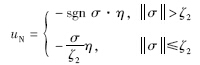
定理1 控制律式(24)保证系统在执行机构故障的情况下,能够在有限的时间内到达滑模面并产生滑模运动,以实现容错,使系统在执行器故障情况下仍能保持一定的性能稳定运行.
证明 取李亚普诺普函数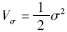 ,则需要证明V·σ在σ≠0时为负.
,则需要证明V·σ在σ≠0时为负.
对李亚普诺普函数求导,得
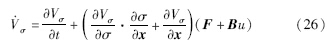
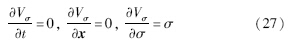
系统的总体控制律:
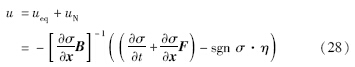
将式(26)、(25)代入(24)中,得到
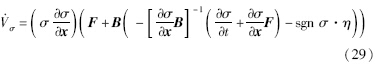
由于滑面并不精确依赖于时间,故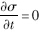 .
.
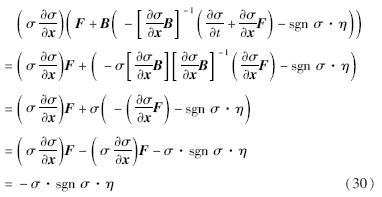
因为σ·sgn σ必大于0,η=f^u(t)+ζζ>0,所以当σ≠0时,式(29)小于0,当且仅当σ=0时V ·σ=0,即在控制律式(22)作用下,满足滑模面的到达条件V·σ≤0,因而能够在有限的时间内到达滑模面产生滑模运动,实现容错控制.
5 仿真分析为了检验基于自适应RBF故障观测的滑模容错控制的有效性,对风能转换系统进行仿真. 系统仿真数据如表 1所示.
| 参数名称 | 参数值 | 参数名称 | 参数值 |
| R | 2.5 m | ρ | 1.25 kg/m3 |
| i0 | 6.25 | η | 0.95 |
| J1 | 3.6 kg·m2 | Cpmax | 0.476 |
| Lt | 150 m | λopt | 7 |
风能转换系统容错控制系统如图 2所示.
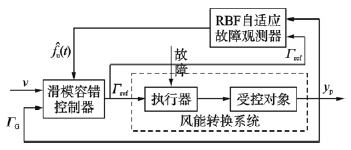 |
| 图 2 风能转换系统滑模容错控制整体框图Fig. 2 Block diagram of WECS sliding mode fault-tolerant control |
功率系数Cp(λ(t))由以下多项式形式给出[20]:
Cp(λ(t))=-4.54×10-7λ7+1.302 7×10-5λ6-
6.541 6×10-5λ5-9.747 7×10-4λ4+
0.008 1λ3-0.001 3λ2+0.006 1λ
用于在线状态估计和故障估计的RBF神经网络结构选为2-11-1,高斯参数选取如下:
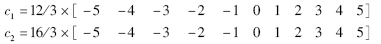
仿真研究中的风速序列如图 3所示.
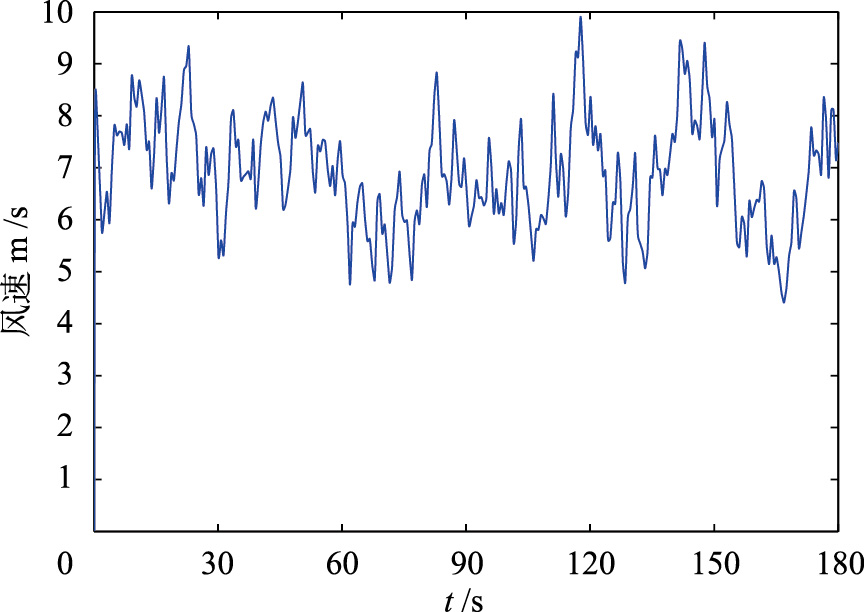 |
| 图 3 风速波形Fig. 3 Wind waveform |
图 4为无故障时风能转换系统电磁转矩状态观测值和实际值对比图,图 5为无故障时风能转换系统转速状态观测值和实际值对比图,图 6为风能转换系统电磁转矩状态、 转速状态观测值和实际值之间误差图.
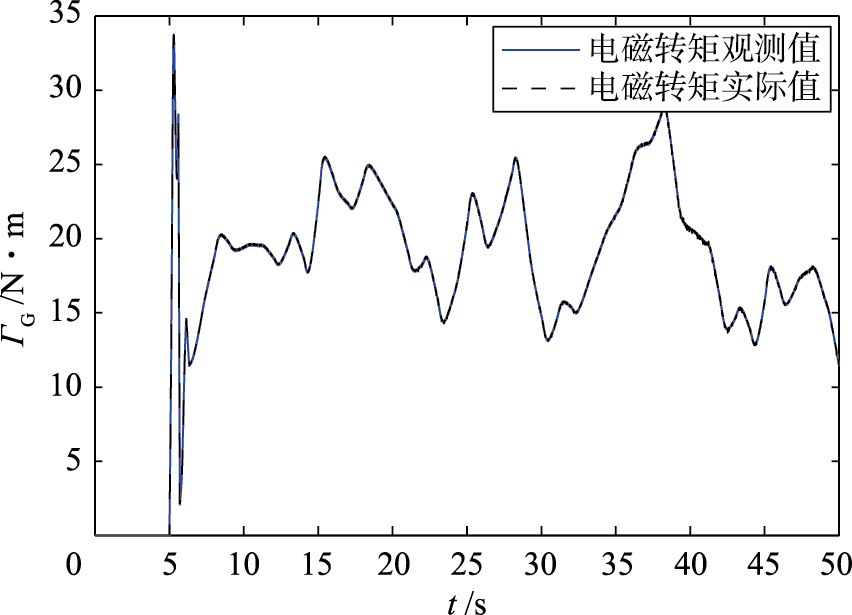 |
| 图 4 风能转换系统电磁转矩状态观测值Fig. 4 Electronic torque state observor values of WECS |
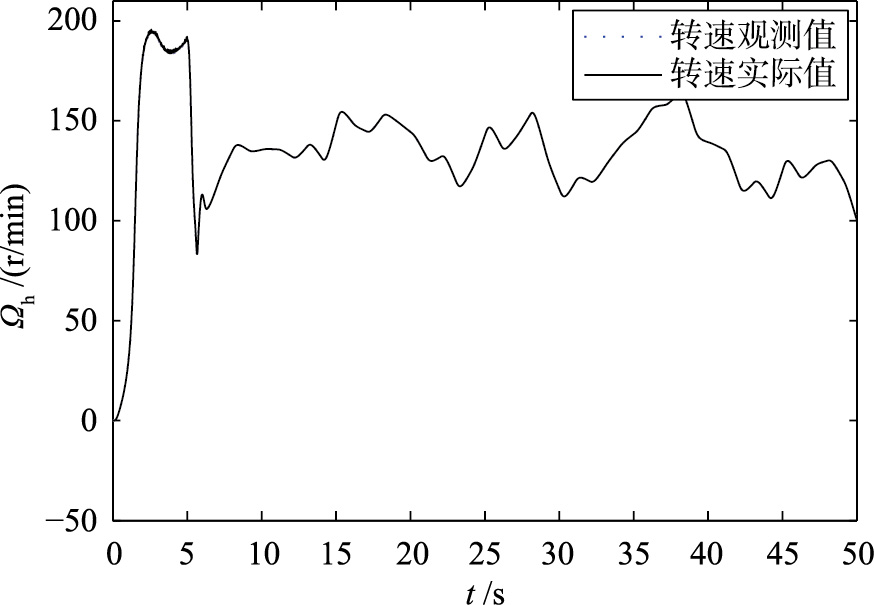 |
| 图 5 风能转换系统转速状态观测值Fig. 5 Speed state observor values of WECS |
 |
| 图 6 风能转换系统状态实际值与观测值误差Fig. 6 Errors between actual state values and state observor values of WECS |
故障类型1: 当系统发生漂移故障时,故障量为ξ(t)=5sin(2πt)cos(2πt),T为故障发生的时间,15 s≤T≤25s,实线代表实际的故障,虚线代表估计的故障,在故障发生前,RBF神经网络的输出为0,当故障发生后,故障估计器较好地估计出系统漂移故障.
如图 8、 9所示,在双馈风能转换系统发生执行器漂移故障时,系统性能恶化并且偏离正常的运行位置,功率系数Cp和叶尖速比λ不能保持在最优值,进而在执行器漂移故障的情况下不能捕获最大风能. 针对自适应RBF观测器估计的执行器漂移故障,变结构滑模容错控制器提高了风能转换系统最大风能捕获效率,达到了容错控制的优化目的,如图 10、 11所示.
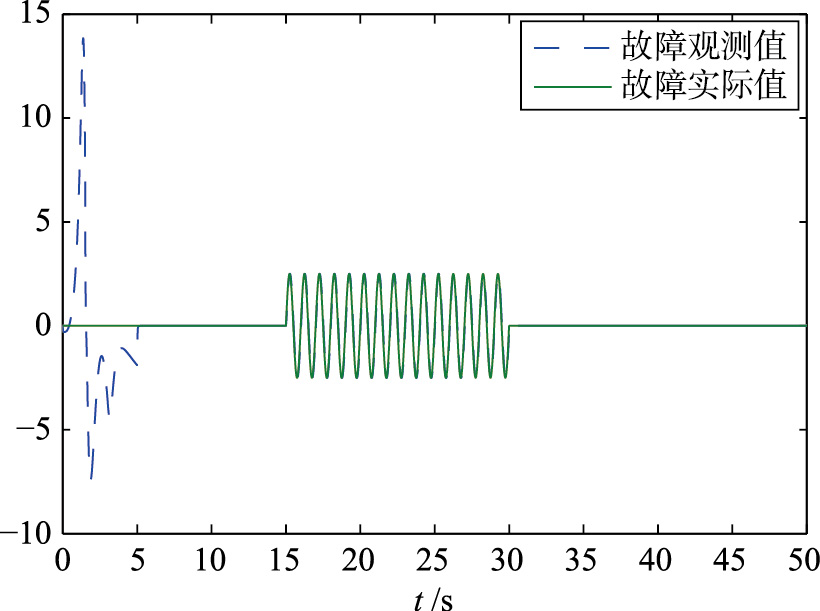 |
| 图 7 执行器实际和重构漂移故障(故障类型1)Fig. 7 Truth and reconstruction drifting fault for actuator |
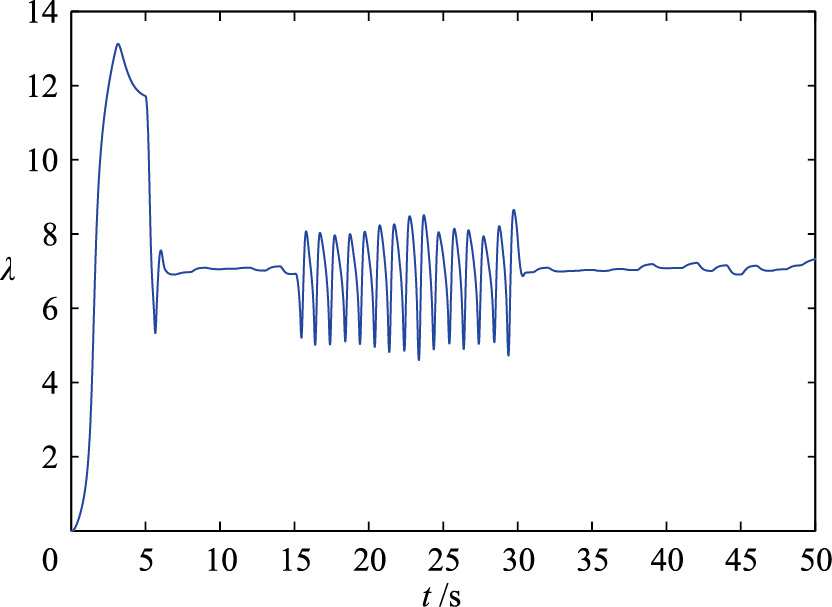 |
| 图 8 执行器漂移故障时叶尖速比(故障类型1)Fig. 8 Tip speed ratio with drifting fault for actuator |
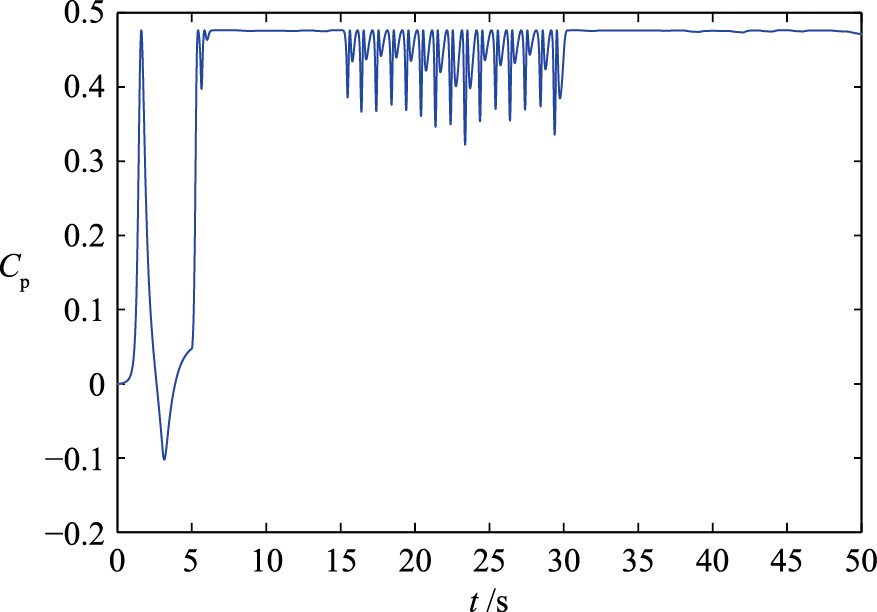 |
| 图 9 执行器漂移故障时功率系数(故障类型1)Fig. 9 Power coefficient with drifting fault for actuator |
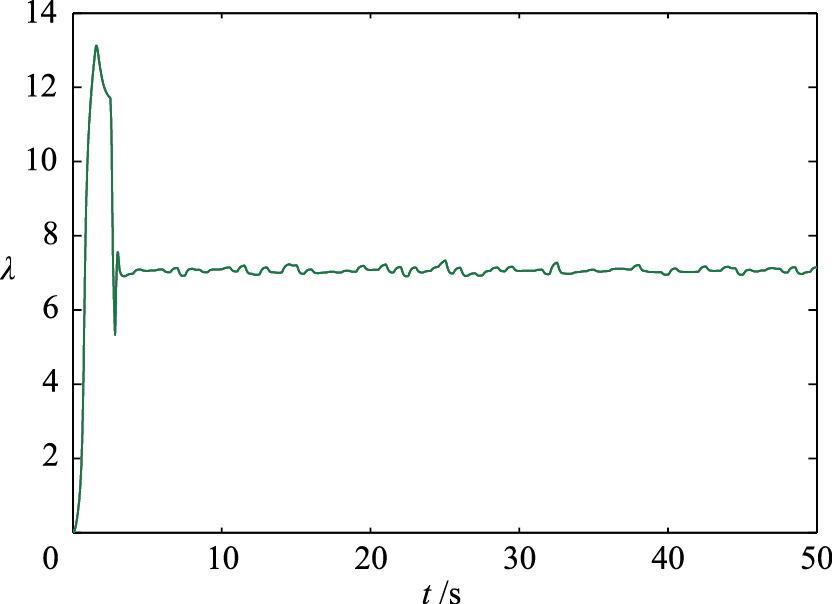 |
| 图 10 执行器漂移故障时滑模容错控制的叶尖速比(故障类型1)Fig. 10 Tip speed ratio under sliding mode fault-tolerant control with actuator drifting fault |
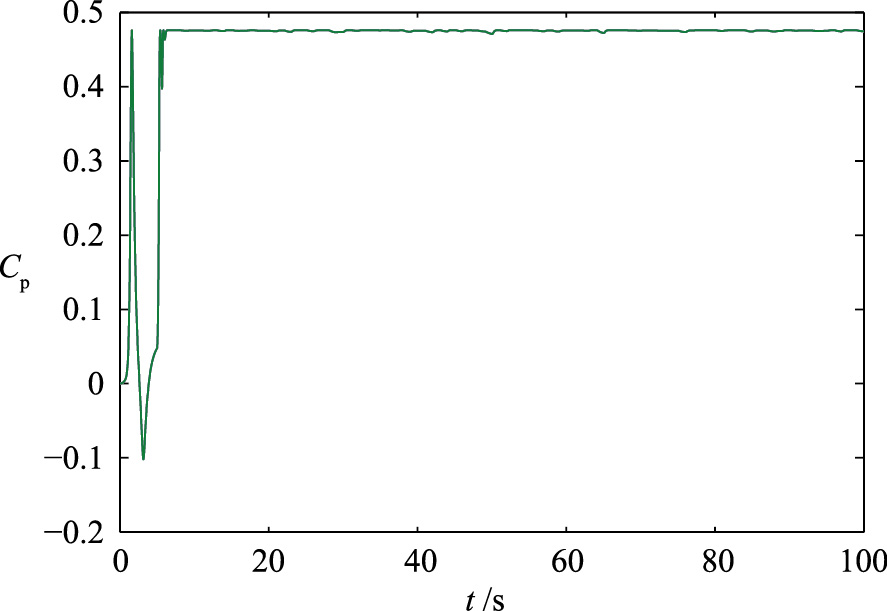 |
| 图 11 执行器漂移故障时滑模容错控制的功率系数(故障类型1)Fig. 11 Power coefficient under sliding mode fault-tolerant control with drifting fault |
故障类型2: 当系统发生偏差故障时,故障量为ξ(t)=5,T为故障发生的时间,15 s≤T≤25s,其它参数不变,实线代表实际的故障,虚线代表估计的故障,在故障发生前,RBF神经网络的输出为0,当故障发生后,故障估计器同样较好地估计出了系统偏差故障.
如图 13、 14所示,在双馈风能转换系统发生执行器偏差故障时,系统性能恶化并且偏离正常的运行位置,功率系数Cp和叶尖速比λ不能保持在最优值,进而在执行器偏差故障的情况下不能捕获最大风能.针对执行器偏差故障,自适应RBF观测器同样能实现故障的精准估计,变结构滑模容错控制器提高了风能转换系统最大风能捕获效率,达到了容错控制的优化目的,如图 15、 16所示.
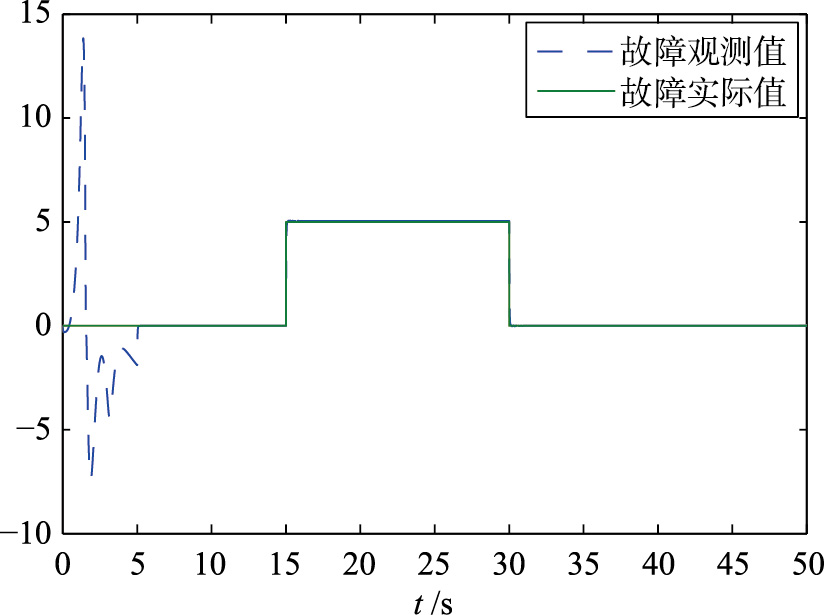 |
| 图 12 执行器实际和重构偏差故障(故障类型2)Fig. 12 Truth and reconstruction deviative fault for actuator |
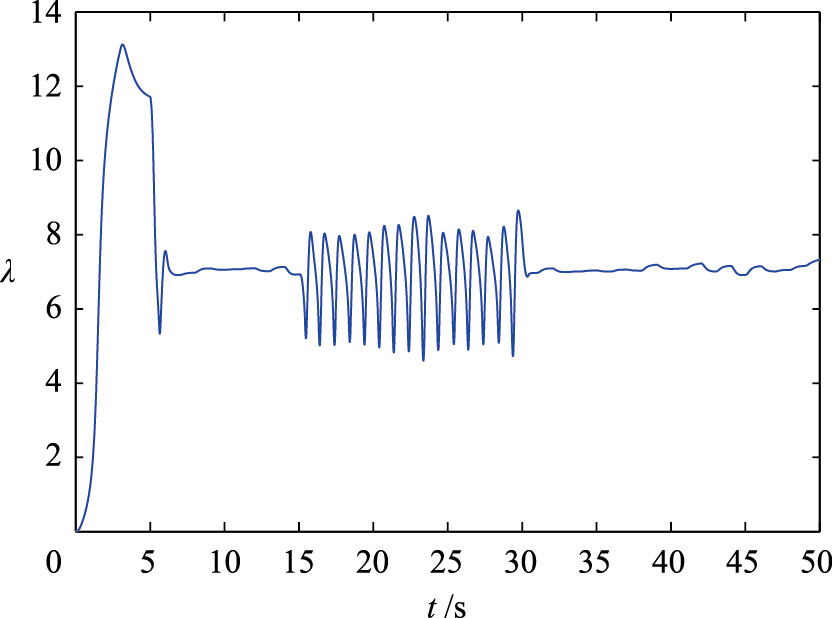 |
| 图 13 执行器偏差故障时叶尖速比(故障类型2)Fig. 13 Tip speed ratio with deviative fault for actuator |
 |
| 图 14 执行器偏差故障时功率系数(故障类型2)Fig. 14 Power coefficient with deviative fault for actuator |
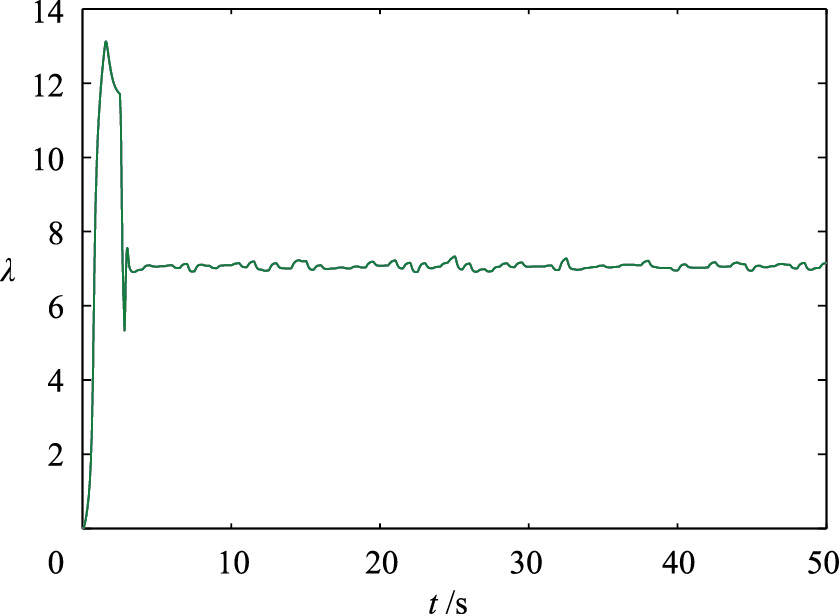 |
| 图 15 执行器偏差故障时采用滑模容错控制的叶尖速比(故障类型2)Fig. 15 Tip speed ratio under sliding mode fault-tolerant control with actuator deviative fault |
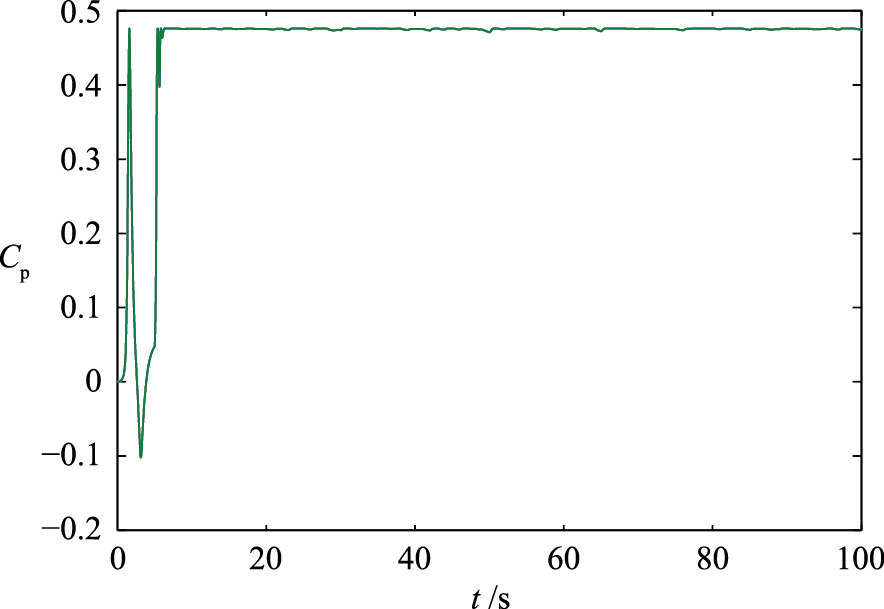 |
| 图 16 执行器偏差故障时采用滑模容错控制的功率系数(故障类型2)Fig. 16 Power coefficient under sliding mode fault-tolerant control with deviative fault |
针对风能转换系统执行器故障,设计的基于自适应RBF观测器的主动容错控制方法,实现了在系统状态不可测的情况下,对执行器故障的精准实时估计,根据故障估计值设计变结构滑模容错控制器,实现故障时的实时容错控制,保证了系统具有可靠的控制输入.
6 结语针对双馈风能转换系统执行器故障,提出了一种基于自适应RBF神经网络故障观测器的风能转换系统主动容错控制策略,在线进行神经网络权值更新,针对系统状态不可测问题,构造RBF神经网络状态估计器观测系统状态量,实现对风能转换系统执行器故障实时高灵敏度的故障检测.在故障准确实时诊断基础上,采用变结构滑模容错控制策略实现系统执行器故障主动容错功能.仿真结果表明,RBF神经网络能实时精准地捕捉到执行器故障;针对故障信息,采用变结构滑模容错控制策略实现系统控制律重构,保证双馈风能转换系统在发生执行器漂移故障和偏差故障时,仍能实现最大风能捕获,稳定运行,进而实现了对系统故障的容错控制,具有广阔的应用前景和价值.
| [1] | Li H, Yang C, Zhao B, et al. Aggregated models and transient performances of a mixed wind farm with different wind turbine generator systems[J]. Electric Power Systems Research, 2012(92): 1-10. |
| [2] | 陈文涛, 谢志红, 陈平. 风能转换机组齿轮箱故障检测与诊断[J]. 机床与液压, 2012, 40(3): 167-169. Chen W T, Xie Z W, Chen P. Fault diagnosis and detection for gearbox of wind turbine generator[J]. Machine Tool & Hydraulics, 2012, 40(3): 167-169. |
| [3] | 高胜利, 赵小荣, 申强. 风能转换机组齿轮箱故障诊断[J]. 电力电子技术, 2011, 45(10): 66-67. Gao S L, Zhao X R, Shen Q. The fault diagnosis of gearbox of the wind turbine[J]. Power Electronics, 2011, 45(10): 66-67. |
| [4] | 杨之俊, 吴红斌, 丁明,等. 故障时双馈风能转换系统的控制策略研究[J]. 电力系统保护与控制, 2010, 38(1): 14-18. Yang Z J, Wu H B, Ding M, et al. Control strategy of doubly-fed wind generation system for power grid fault[J]. Power System Protection and Control, 2010, 38(1): 14-18. |
| [5] | Hang J, Zhang J Z, Cheng M, et al. An overview of condition monitoring and fault diagnostic for wind energy conversion system[J]. Transaction of China Electrotechnical Society, 2013, 28(4): 261-271. |
| [6] | 撖奥洋, 张哲, 尹项根, 等. 双馈风能转换系统故障特性及保护方案构建[J]. 电工技术学报, 2012(27): 233-239. Han A Y, Zhang Z, Yin X G, et al. Research on fault characteristic and grid connecting-point protection scheme for wind power generation with doubly-fed induction generator[J]. Transaction of China Electrotechnical Society, 2012(27): 233-239. |
| [7] | 吴定会, 李意扬, 纪志成, 等. 风力机的线性变参数主动容错控制[J]. 控制理论与应用, 2014, 31(4): 425-430. Wu D H, Li Y Y, Ji Z C. Active fault-tolerant linear-parameter-varying control of wind turbines[J]. Control Theory & Applications, 2014, 31(4): 425-430. |
| [8] | 李辉, 赵猛, 赵斌, 等. 双馈风电机组转速观测及容错控制策略[J]. 电力系统自动化, 2011, 35(1): 77-82. Li H, Zhao M, Zhao B, et al. Studies on the rotor speed observation and fault-tolerant control strategy for wind turbine driven doubly-fed induction generator[J]. Automation of Electric Power Systems, 2011, 35(1): 77-82. |
| [9] | He Q N, Shen Y X, Ji L Y. Fault tolerant control strategy for nonlinear system based on feedback control[C]//Proceedings of the American Control Conference. Piscataway, NJ, USA: IEEE, 2013: 4897-4902. |
| [10] | Muhando E B, Senjyu T, Kinjo H, et al. Augmented LQG controller for enhancement of online dynamic performance for WTG system[J]. Renewable energy, 2008, 33(8): 1942-1952. |
| [11] | Bianchi F, De Battista H, Mantz R J. Wind turbine control systems[M]. Berlin, Germany: Springer, 2006: 20-47. |
| [12] | Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on System, Man, and Cybernetics, 1985, 15(2): 116-132. |
| [13] | Kamal E, Aitouche A, Ghorbani R, et al. Robust fuzzy fault-tolerant control of wind energy conversion systems subject to sensor faults[J]. IEEE Transactions on Sustainable Energy, 2012, 3(2): 231-241. |
| [14] | 沈艳霞, 贺庆楠, 潘庭龙, 等. 风能转换系统T-S模糊鲁棒容错控制[J]. 信息与控制, 2013, 42(6): 750-757, 764. Shen Y X, He Q N, Pan T L, et al. T-S fuzzy robust fault-tolerant control strategy for wind energy conversion system[J]. Information and Control, 2013, 42(6): 750-757, 764. |
| [15] | Hong C M, Cheng F S, Chen C H. Optimal control for variable-speed wind generation systems using general regression neural network[J]. International Journal of Electrical Power & Energy Systems, 2014(60): 14-23. |
| [16] | 邓涛, 姚宏, 杜军, 等. 高阶非线性系统的神经网络动态面控制[J]. 系统工程与电子技术, 2013, 35(11): 2384-2389. Deng T, Yao H, Du J, et al. Neural network dynamic surface control for high-order nonlinear systems[J]. Systems Engineering and Electronics, 2013, 35(11): 2384-2389. |
| [17] | Esbensen T, Sloth C. Fault diagnosis and fault-tolerant control of wind turbines[M]. Aalborg, Denmark: Aalborg University, 2008: 9-23. |
| [18] | Munteanu I, Bratcu A I, Cutululis N A, et al. Optimal control of wind energy systems: Towards a global approach[M]. Berlin, Germany: Springer, 2008: 150-158. |
| [19] | Yang G, Li H. Twi-sliding mode control for efficiency improvement in variable speed small wind turbine systems[C]//Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation. Piscataway, NJ, USA: IEEE, 2007: 3717-3723. |
| [20] | 孟涛, 沈艳霞, 纪志成. 基于风能转换系统的T-S模糊建模与控制[J]. 微特电机, 2011(10): 68-72. Meng T, Shen Y X, Ji Z C. Wind energy conversion systems using T-S fuzzy modeling[J]. Small & Special Electrical Machines, 2011(10): 68-72. |



