1 引言
近年来,无线传感器网络[1](wireless sensor network,WSN)得到了快速的发展. 由于其具有能耗低、 体积小、 成本低等优势,而被广泛应用于生产、 生活的各个领域. 确定位置信息,始终是无线传感器网络的研究热点之一,也使得WSN定位技术成为了研究的重要内容. 定位算法通常可以分为基于非测距(range-free)和基于测距(range-based)[2, 3]两种,实际应用中,基于测距的算法精度往往更高,从而得到了更广泛的应用.
文[4]提出基于图论模糊聚类的室内自适应RSSI定位算法,实时性较好,但是不适用于环境变化较大的情况. 文[5]使用改进的RSSI多维标度定位算法,但是算法前期准备较为复杂. 文[6]提出一种基于区间数聚类的RSSI测距方法,但是无法对参数进行自适应调节. 文[7]提出将卡尔曼滤波算法应用于跟踪定位,但是如果环境较为复杂,偏差将很大,适应环境能力不强.
对无线传感器网络来说,通常是使用基于接收信号强度指示(received signal strength indication,RSSI)来确定位置信息. 此方法主要是依据读取无线网络各节点的RSSI值,再通过建立RSSI值与距离之间的数学模型,以此求得各节点的相对位置,最后通过一些定位算法求取所需节点的位置. 虽然RSSI定位方式实现较为简单,但是在实际操作中,由于无线信号往往会被障碍物吸收、 反射,还会发生多径效应等,因此,传统的RSSI定位精度通常不高.
针对上述问题,将引力搜索算法[8](gravitational search algorithm,GSA)引入RSSI定位方法中. 先用极大似然估计法得到RSSI测距模型的修正参数,求取节点间的相对位置,通过最小二乘法(least square method,LSM)求取所需节点坐标,再通过GSA对LSM的坐标估计结果和参数进行优化,不仅可以提高节点坐标的精度,还可以实现动态跟踪参数变化.
2 RSSI定位模型 2.1 基本RSSI模型的分析具体研究中,通常使用式(1)所示的RSSI定位模型[4]:


一般的RSSI定位都是直接将a和b的经验值代入公式进行计算,此方法偏差较大. 若使用若干的RSSI和d值进行最小二乘拟合[10]来求取对应的a和b,需要的数据过多,精度也并不是很好. 这里使用极大似然估计法(maximum likelihood estimation,MLE)进行校正,对于若干个参考节点与盲节点的关系如式(3)所示:
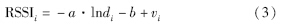



通过极大似然估计法求出的参数能够较好地利用已知信息,提高了求取估计坐标的精度.
3 最小二乘法初步求取估计坐标将式(6)求解出来的参数代入式(2),通过读取RSSI值求出盲节点和参考节点的相对距离d,使用最小二乘法初步计算出参考节点的估计坐标,可以得到较为精确的位置[11],即式(7):
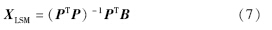

这样得到的估计坐标在环境不变时可以得到较好的结果. 但实际过程中,环境是不断变化的,因此,通过一些智能算法对估计结果进行优化,提高适应环境的能力,还是很有必要的,这里使用引力搜索算法(GSA)对估算的定位结果进行优化.
4 引力搜索算法优化估计坐标在一些情况下,环境条件可能发生较大变化,这时由一系列的已知数据而建立的数学模型就已经不再适用,如式(2)中先求取的参数a、 b本身就随着环境剧烈变化,自然就不能将其当成定值来计算出位置信息. 这时,就需要动态整定出参数及位置坐标. 也就是说,前面求取的参数和利用参数求取的坐标只能作为初步估计以提供算法的优化范围.
引力搜索算法是由伊朗的克曼大学教授Rashedi等人提出来的优化算法,使用改进的引力搜索算法对估计坐标进行优化. 设所求的盲节点最终坐标为(x,y),通过式(7)计算出来的估计值为(x′,y′),则x∈(x′-ε,x′+ε),y∈(y′-ε,y′+ε),ε表示自己选取的正数,本文称为调节因子,用来调节优化的范围. 当然,也可以将x和y的取值放大为整个可以取值的区域,这样就不需要使用最小二乘法初步估计,但是增加了计算机的负担,降低了求解的效率. 对最小二乘法的估计结果进行优化大大缩小了优化范围,减小了算法带来的的误差.
对于RSSI定位模型,a∈(-40,-10),b∈(-50,-30). 由于读取出来的RSSI值通常是绝对值,因此,利用RSSI绝对值计算的a、 b均为负数.
在上述x、 y、 a、 b的范围内随机产生N个粒子,第i个粒子的位置为Xi=(x1i,x2i,x3i,x4i),其中x1i、 x2i、 x3i、 x4i分别对应于所要求取的x、 y、 a、 b. 选取的粒子数越多结果越精确,运算量也越大. 使用xdi表示该粒子在第d维上的位置. 在t时刻(也即为第t次迭代),第d维上第i个粒子所受到的总的作用力是其它适应度最大的粒子对其作用力之和,如下式[12]:



确定了此时作用力之后,依据牛顿第二定律求解此时的加速度:

然后更新速度和位置信息:

另外,惯性质量也需要更新,其与适应度函数的大小相关,意味着惯性质量越大,有越大的吸引力,也越接近所求得的最优值. 其计算方法如下:


可以使用式(19)作为其适应度函数,即:

如此,通过GSA训练出来的最终结果Xm=(x,y,a,b),不仅可以得到较高的定位精度,还能够描述出此时的RSSI模型的参数a、 b. 由于环境的变化的影响是通过参数a、 b表现出来,说明此方法实现了对盲节点坐标和模型参数的动态跟踪变化,a、 b将此种方法称为MLE-LSM-GSA.
5 仿真和实验 5.1 实验准备和数据预处理实验使用的设备是尚阳公司开发的CC2430[13],实验地点为实验室,试验范围是6m×6m,实验室有非常多的实验设备、桌椅、人员等障碍物,而且实验室电子设备随时开启,可能会有多种电子信号干扰,再加上人员、 设备、 桌椅的频繁移动,可以看作是环境变化的RSSI的定位实验,实验环境如图 1所示.
 |
| 图 1 实验环境Fig. 1 Experimental environment |
系统误差由测试的平均定位误差描述:
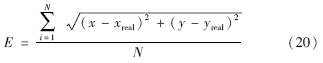
实验参考节点坐标为(0,0)、 (6,0)、 (0,6)、 (6,6)、 (3,0)、 (0,3)、 (6,3)、 (3,6),单位是m. 通过已知的10组盲节点坐标以及发送广播后对应的RSSI值(RSSI值全取绝对值,对应参数为负数),按照MLE可以求得估计参数a=-23.374 5,b=-44.395 7,通过极大似然—最小二乘法(MLE-LSM),极大似然—最小二乘法—引力搜索算法优化(MLE-LSM-GSA)两种算法求取所需的参数、 坐标和误差.
5.2 Matlab仿真与结果分析为了从理论上说明GSA算法对结果的优化能力和对环境的适应能力,在上述环境条件下进行Matlab仿真. 对环境的干扰进行设置,假设对于式(5)中环境的干扰服从高斯分布(0,δ2),改变δ的值,观察各变量的变化. 本次仿真将盲节点从坐标(5,1)沿直线运动到(1,5),均匀选取运动轨迹中的100个点,每个点采样50次,利用两种方法得到的轨迹,最终求出的a、 b随横坐标的变化及误差的平均值. GSA优化的粒子数N为30个,调节因子取0.2. δ分别取2、 3、 4、 5以模拟环境变化,两种算法得出的结果如图 2~4所示. 各图横坐标均为盲节点沿x轴的坐标变化,图 2中的图(a)、 (b)、 (c)、 (d)分别为δ分别取2、 3、 4、 5时参数a的值,(e)、 (f)、 (g)、 (h)为参数b的值,图 3中的(a)、 (b)、 (c)、 (d)为各位置的平均误差,图 4中的(a)、 (b)、 (c)、 (d)为最终的坐标估计. 表 1给出了δ取不同值时对应的累加均方根误差.
 |
| 图 2 MLE和MLE-LSM-GSA对参数的估计Fig. 2 The parameters estimation between MLE and MLE-LSM-GSA |
 |
| 图 3 各算法的平均误差分布Fig. 3 The distribution of average error in different algorithms |
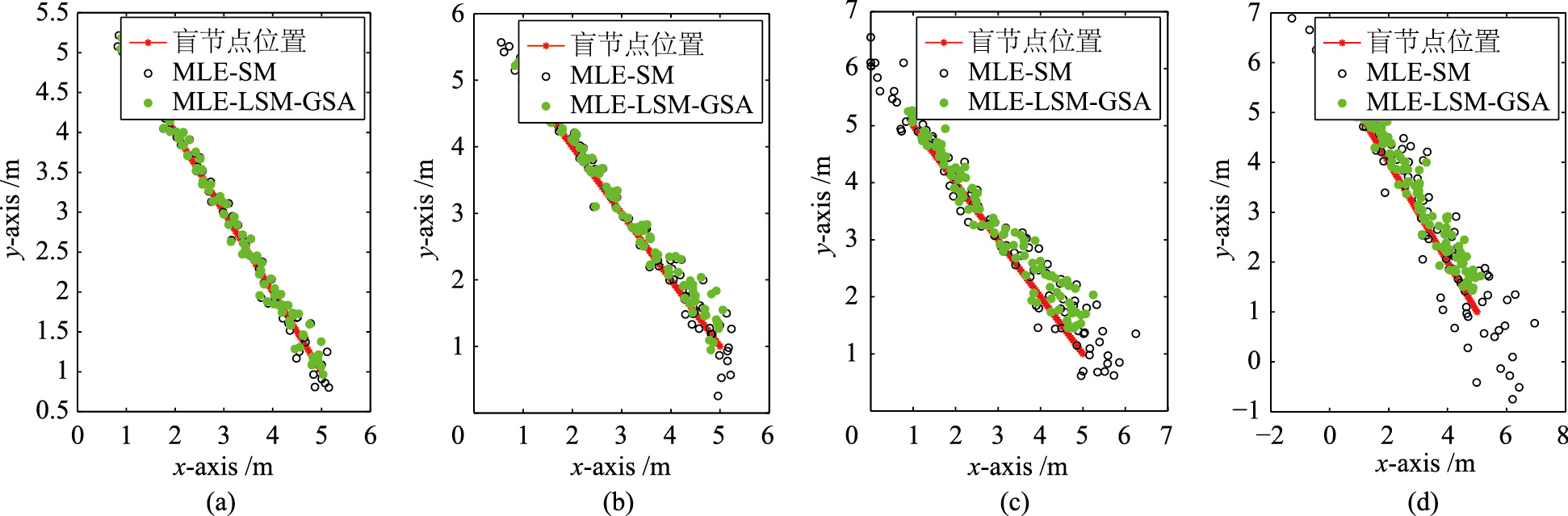 |
| 图 4 各算法的坐标估计Fig. 4 The coordinate estimation by different algorithms |
| 算法 | δ | |||
| 2 | 3 | 4 | 5 | |
| MLE-LSM | 0.168 5 | 0.299 5 | 0.648 6 | 1.094 0 |
| MLE-LSM-GSA | 0.146 3 | 0.223 9 | 0.383 9 | 0.448 4 |
从图 2可以看到,随着位置的变化,参数a、 b也随之改变,实现了参数的动态跟踪,从而使得系统具备了适应环境的能力. 图 3的误差分布清楚地显示了随着δ增大,各算法的误差也有明显增大的趋势,但是从各算法的误差分布情况来看,MLE-LSM-GSA误差增大的幅度明显小于MLE-LSM,保持了较高的精度. 从表 1的累加均方根误差来看就更能说明上述事实,当δ=2时,MLE-LSM-GSA误差仅比MLE-LSM小0.022 2,减少了13.18%,但是随着δ增大,误差的差距越来越大,当δ=5时,MLE-LSM的累加均方根误差达到MLE-LSM-GSA的2.440倍.说明经过GSA优化后不仅提高了原来估计坐标的定位精度,而且对环境变化的适应能力更强. 从图 4中可以直观地看到各算法的定位效果图.
5.3 实际操作结果选取实验室的10个不同位置,将盲节点放在这10个位置对参考节点发送广播,取出RSSI值,同样通过上述两种不同方法求取其位置. 在不同的时间点将盲节点上述10个位置,测试20次,以模拟环境的变化,得到的结果如表 2、 表 3所示[9]. 从实际操作的实验结果可以看到经过GSA优化后误差减小,验证了算法的正确性.
| 时刻 | 参数 | |
| a | b | |
| 9 | -10.000 2 | -39.084 3 |
| 11 | -19.996 6 | -36.896 6 |
| 13 | -19.998 1 | -34.796 8 |
| 15 | -14.878 3 | -42.233 5 |
| 17 | -17.982 7 | -40.023 8 |
| 19 | -19.995 2 | -48.739 4 |
| 21 | -18.222 4 | 39.338 7 |
| 算法 | 误差 |
| MLE-LSM | 2.038 9 |
| MLE-LSM-GSA | 1.214 2 |
实验结果表明,将引力搜索算法应用于RSSI定位算法后,减弱了数学模型对于环境的依赖性,提高了系统自适应能力,从而提高了RSSI定位算法精度.关于如何确定使用GSA中盲节点位置的搜索范围以使得定位精度更高,仍然值得进一步研究.此外,使用GSA时也有可能会陷入局部最小值,因此,将GSA算法引入RSSI定位中,如何规避局部最小值,仍然是值得研究的重要课题.
| [1] | Wang F B, Shi L, Ren F Y. Self-location systems and algorithms for wireless sensor networks[J]. Journal of Software, 2005, 16(5): 857-868. |
| [2] | He T, Huang C D, Blum B M, et al. Range-free localization schemes in large scale sensor networks[C]//Proceedings of the Ninth Annual International Conference on Mobile Computing and Networking. New York, USA: ACM, 2003: 81-95. |
| [3] | 林金朝, 陈晓冰, 刘海波. 基于平均跳距修正的无线传感器网络节点迭代定位算法[J]. 通信学报, 2009, 30(10): 107-113. Lin J C, Chen X B, Liu H B. Iterative algorithm for locating nodes in WSN based on modifying average hopping distances[J]. Journal on Communications, 2009, 30(10): 107-113. [4] 高鹏, 石为人, 周伟, 等. 基于图论模糊聚类的室内自适应RSSI定位算法[J]. 仪器仪表学报, 2013, 34(9): 1998-2004. Gao P, Shi W R, Zhou W, et al. Indoor adaptive RSSI localization algorithm based on graph theory and fuzzy clustering in wireless sensor networks[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 1998-2004. |
| [5] | 石欣, 印爱民, 陈曦. 基于RSSI的多维标度室内定位算法[J]. 仪器仪表学报, 2014, 35(2): 261-268. Shi X, Yin A M, Chen X. RSSI and multidimensional scaling based indoor localization algorithm[J]. Chinese Journal of Scientific Instrument, 2014, 35(2): 261-268. |
| [6] | 彭宇, 罗清华, 王丹, 等. 一种基于区间数聚类的RSSI-D估计方法[J]. 仪器仪表学报, 2012, 33(3): 491-498. Peng Y, Luo Q H, Wang D, et al. WSNs distance estimation method with RSSI-D using interval data clustering algorithm[J]. Chinese Journal of Scientific Instrument, 2012, 33(3): 491-498. |
| [7] | Caceres M A, Sottile F, Spirito M A. Adaptive location tracking by Kalman filter in wireless sensor networks[C]//Proceedings of the 5th IEEE International Conference on Wireless and Mobile Computing Networking and Communication. Piscataway, NJ, USA: IEEE, 2009: 123-128. |
| [8] | Rashedi E, Nezamabadi-pour H, Saryazdi S. GSA: A gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232-2248. |
| [9] | 刘颖, 苏俊峰, 朱明强. 基于迭代容积粒子滤波的蒙特卡洛定位算法[J]. 信息与控制, 2012, 42(5): 632-638. Liu Y, Su J F, Zhu M Q. A Monte-Carlo localization algorithm based on iterated cubature particle filter[J]. Information and Control, 2012, 42(5): 632-638. |
| [10] | Sun P G, Zhao H, Luo D D, et al. Research on RSSI-based location in smart space[J]. Acta Electronica Sinica, 2007, 35(7): 1240-1245. |
| [11] | Niculescu D S, Nath B. Localized positioning in ad hoc network[C]//Proceedings of the 1st IEEE International Workshop on Sensor Network Protocols and Applications. Piscataway, NJ, USA: IEEE, 2002: 42-44. |
| [12] | 徐遥, 王士同. 引力搜索算法的改进[J]. 计算机工程与应用, 2011, 47(35): 188-192. Xu Y, Wang S T. Enhanced version of gravitational search algorithm: Weighted GSA[J]. Computer Engineering and Applications, 2011, 47(35): 188-192. |
| [13] | 刘颖, 苏军峰, 朱明强. 基于平方根容积卡尔曼滤波的RSSI定位参数估计算法[J]. 系统仿真学报, 2014, 26(1): 119-124. Liu Y, Su J F, Zhu M Q. Received signal strength indicator parameter estimation algorithm based on square-root cubature Kalman filter[J]. Journal of System Simulation, 2014, 26(1): 119-124. |



