1 引言
近年来，分布式卡尔曼一致性滤波算法因其收敛速度快、 融合精度高等特点，被广泛应用于无线传感器网络信息融合技术中[1, 2, 3, 4, 5, 6, 7]. 但大多已提出的算法都以随机几何图为拓扑结构，其通信复杂度较高. 其次，考虑到传感器节点能量、 带宽、 信息计算、 存储等资源都相当有限，因此在保证一定滤波精度的条件下，如何设计有效的分布式滤波算法，最大化网络生命周期是无线传感器网络协议涉及的首要目标[8]. 分簇路由算法正是满足这些要求的行之有效的网络级分布式算法之一[9, 10, 11, 12, 13, 14, 15].
分簇路由算法可以把无线传感器网络分成簇内和簇头两种网络层次. 结合无线节点通信损耗能量同传送的数据量和到达目标距离的幂次方成正比的特性[16]，考虑在分簇算法的基础上，采用能有效减少通信次数的Gossip算法[17]来进一步减少簇头级网络的数据传输量，以降低网络通信能量消耗.
本文研究了一种分布式分簇卡尔曼一致性滤波算法. 在该算法中，每个簇由一个簇头和若干簇内部节点组成，簇头节点融合簇成员节点的信息，并在邻居簇头间就融合信息进行一致性处理. 通过应用图论、 矩阵论对算法进行收敛分析，找出网络拓扑结构、 算法参数、 能量消耗之间的关系. 在此基础上，进一步研究了Gossip算法在分布式卡尔曼滤波中的应用. 最后，应用模拟仿真对算法进行验证，并与已有典型的分布式卡尔曼一致性滤波算法从滤波精度、 能量消耗两个方面分别进行了对比.
2 相关工作 2.1 问题描述
定义G=(V，E，A)为一个加权无向图，其中V=｛1，…，n｝为顶点集合； E⊆V×V为边集合. A=｛aij｝∈Rn×n为邻接矩阵，其元素aij表示节点i与节点j之间是否有连接. 定义节点i的邻居集合为Ni=｛j∈V： (i，j)∈E｝，那么节点i的度为di=N(i). 图G的拉普拉斯矩阵定义为L=D-A，其中，D=diag｛d1，d2，…，dn｝. 如果网络连通，矩阵L的特征值满足λ1(L)≥λ2(L)≥…≥λn(L)=0[18]且λ1(L)≤2dmax，其中dmax=maxi∈Vdi. 为了确保图G以较高的概率(1-1/n2)连通[19]，对于单位区域内所有节点其传输半径r(n)满足
(如图 1所示随机几何图). 目标系统的状态模型和传感器的观测模型为
.
 |
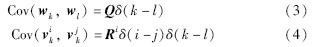
| 图 1 随机几何图(节点数n=500，边数l=3 442)Fig. 1 Random geometric graph with n=500 nodes and l=3 442 links |
将检测区域划分为若干大小相同的虚拟单元格，位于同一个单元格内的节点为一个簇. 同时，单元格边长a的选取需保证相邻两格内任意两个节点能相互通讯，即a≤
(ro为节点的最大通信半径). 对于簇头节点的确定，这里，以周期性的方式选取能量较高的节点来担任簇头. 分簇结果如图 2所示(实心圆点表示簇头节点，空心圆点表示簇成员节点)，簇头节点之间保持全连通.
 |
| 图 2 分簇拓扑图Fig. 2 Clustering topology |
文[4]以一致性策略融合各节点邻居节点的估计信息提出了几种分布式卡尔曼一致性滤波算法，是较为经典的滤波算法. 但所有算法都以随机几何图为拓扑结构，其通信复杂度较高. 为此，将无线传感器网络进行分簇处理，分簇过程如2.2小节中描述.
定义图G=(V，E)的子图为G^，以Ci表示簇i的所有簇成员节点，N^j表示簇头节点j的邻居簇头节点.
对于如下所示基于簇的离散一致性迭代方程：
在给出主要结论前，首先给出下面定义：
定义1[20] 对于确定一致性算法，定义其渐近收敛因子为
其中，xave=(1·1T/n)·x0，1=(1，…，1)T，相应ε-平均收敛时间为
定理1 对于簇头级无向网络拓扑G^=(V^，E^)，由方程(5)，给定任意初始状态x0，若取α*=2/(λ1(L^)+λm-1(L^))，那么算法能以大于或等于=1-α*λm-1(L^)的速度全局指数收敛到均衡值. 且对应的ε-平均时间为T^ave(ε)=ln ε-1/2b^，其中，b^=λm-1(L^)/λ1(L^).
证明 由方程xk+1=W^·xk知，若系统能收敛至初始平均值，则极限
xk=(1·1T/m)·x0成立，也即(W^k-1·1T/m)=0成立. 由于G^为无向连通网络，则矩阵W^为双随机矩阵，那么
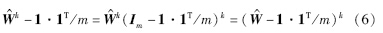
(W^-1·1T/m)k=0，该式成立的条件是矩阵W^-1·1T/m的谱半径必须小于1. 由于矩阵L^半正定，那么矩阵W^的特征值可以表示为
由于矩阵W^的最大特征值为1，其它特征值在数值上都小于1，且矩阵W^的1特征值对应矩阵L^的零特征值，即λm(L^)=0，λ1(W^)=1. 那么：
因此，要保证ρ(W^-1·1T/m)<1，只需：
结合定义1渐近收敛因子的表达式，可知：
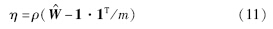
由于系统的收敛速度取决于谱半径的大小，当一致性增益α满足
时，有：
相反，当
时，有：
因此，在ρ<1的情况下，取可以达到最优收敛速度
下面证明ε-平均收敛时间，由
，这里，如果定义
，那么
由于
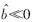，因此，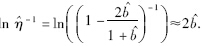
结合定义1，其最优ε-平均时间为
评论1 由定理1可以发现，系统的最优收敛速度和相应的ε-平均收敛时间取决于网络图拉普拉斯矩阵L^的最大和非零最小特征值.下面给出在不同节点数量情况下，本文分簇拓扑结构与随机几何拓扑结构的谱性质及ε-平均收敛时间比对表.
由表 1可以看出，由于分簇处理，提高了网络的代数连通度. 在达到同等收敛精度条件下，仅从拓扑结构考虑，本文簇结构比随机几何拓扑结构能缩短至少3倍时间. 基于以上分析，本文提出分布式分簇卡尔曼一致滤波算法：各簇成员节点周期性地采集被估计目标状态，并将信息发送给簇头节点，簇头节点融合该信息进行集中式卡尔曼滤波.然后，各簇头节点广播自己的融合信息给其它邻居簇头，并在簇间就该信息进行一致处理以估计目标状态.
| 节点数 | 随机几何拓扑结构 | 分簇拓扑结构 | ε-平均收敛时间比值Tave(ε)/T^ave(ε) | ||
| λn-1(LT^) | λ1(L) | λn-1(L^) | λ1(L^) | ||
| 25 | 2.345 2 | 19.193 3 | 4.116 6 | 11.411 7 | 2.950 0 |
| 60 | 2.299 9 | 31.576 8 | 3.700 5 | 13.058 7 | 3.892 9 |
| 100 | 2.169 6 | 33.742 7 | 3.242 2 | 13.565 7 | 3.717 0 |
| 160 | 2.024 8 | 37.152 3 | 2.819 4 | 14.631 0 | 3.534 2 |
算法1 分布式分簇卡尔曼一致性滤波算法步骤
1) 初始化：
2) 所有簇成员节点观测目标状态信息zi.
3) 各簇簇成员节点发送观测信息zi给簇头节点.
4) 各簇头节点融合簇成员节点发送的信息：
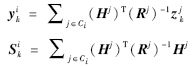
5) 各簇头节点计算局部卡尔曼滤波估计值：
6) 各簇头节点广播信息mi=｛φi}给其邻居簇头节点并计算一致性估计值：
7) 各簇头节点更新局部卡尔曼滤波状态：
8) 返回步骤2).
评论2 算法1较之于Olfati算法，其每个时刻簇头节点只需要传送m位数据，而Olfati算法需要传送n2+3n位数据. 因此，分簇处理能够有效地减少数据传输量和缩短传送距离，从而降低能量消耗.
3.2 分簇卡尔曼Gossip滤波为进一步节省网络能量，本文基于提出的分簇模型，给出了分簇卡尔曼Gossip滤波算法2. 各簇头节点与邻居簇头节点的连接概率为[12]： 在每一步计算中，所有节点随机且独立地以1/2的概率激活； 对于激活节点i，该节点以概率1/d*(d*为网络最大度)从其di个邻居节点中任选一个进行通信，而以概率1-di/d*不与任何节点连接. 在算法2中，同一时间间隙内相互通信的多对传感器节点互不冲突，而不进行信息通信的簇进入休眠状态. 下面给出算法2的滤波步骤.
该算法相对于算法1仅对步骤6)做如下修改，其它保持不变：
6) 各簇头节点传送信息mi=｛φi｝给其可连接邻居簇头节点并计算平均估计值：
例1 考虑将500个传感器节点随机布置在单位面积的正方形检测区域内. 对于Olfati算法，所有传感器节点通讯半径为r=0.15. 对于本文所提出的算法1和2，簇头节点的通讯半径为ro=0.223 6. 待检测目标状态： X(t)=sint+sin(2t+3)+sin(5t+4)，过程噪声协方差Q=0.5，初始条件x0=1，Pi0=1. 对所有的传感器节点，取观测噪声协方差Ri=0.3.
4.1 3种算法滤波效果的仿真对比
为了比较本文算法与Olfati算法的估计性能，定义平均估计误差
和平均一致性误差
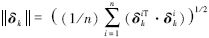，其中
，
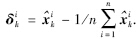仿真结果如图 3、 4所示.
 |
| 图 3 平均估计性误差比较Fig. 3 Comparison of average estimation errors |
 |
| 图 4 平均一致性误差比较Fig. 4 Comparison of average consensus errors |
从图 3和图 4可以看出，本文中给出的算法1两种误差都小于Olfati算法，而算法2的误差稍大于Olfati算法. 其原因是Olfati算法对应的b=0.002 4，而算法1中b^=0.012 5. 因此，在达到相同收敛精度时算法1所需要的时间能缩短至少3倍左右. 对于算法2，由于降低了网络的连通度，进而延长了系统的收敛时间.
4.2 步长对估计精度的影响依旧考虑例1中的系统模型，仿真结果如图 5所示. 由图 5可以看出，对于算法1，当步长取值在0.2左右时收敛误差达到最小值，当取值大于临界值αmax=0.256 3时，算法误差将会急剧增大. 对于Olfati算法，当步长大于0.15时误差也将急剧增大. 这表明对于任意一组给定的系统参数，当步长取为最优时，估计误差达到最小，而当超过某一个临界值时，算法收敛速度将变慢. 且由图 5可以发现取最优步长时，算法1的收敛精度要高于Olfati算法.
 |
| 图 5 步长与收敛误差的关系Fig. 5 Comparing step-size with consensus errors |
4.3 3种算法能量消耗对比
在本文中，采用文[13]中给出的能量消耗模型. 在初始状态，假定每个传感器节点的能量为2 J，对应单元格的能量和在4 J~18 J之间. 仿真时，取Eelec=50 nJ/bit，εamp=100 pJ/bit/m2，l=5 000 bit，c=2. 取节点融合消耗能量EDA=5 nJ/bit/signal. 下面给出这3种算法的能量消耗仿真图. 对于Olfati算法，为了便于比较，也同样统计虚拟单元格内所有传感器节点能量消耗.
在图 6～8中，将簇单元剩余能量值从小到大做了排序. 图 6中，由于每个节点传递的信息量过多，消耗的能量随之也增多，大概在300步后就有部分簇单元节点能量完全消耗完. 在同样的条件下，本文所提出的算法由于减少了大量冗余信息，节省了很大一部分能量. 对于算法1，在1 400步左右簇单元能量会完全消耗完，整个传感器网络的寿命延长了大概4.5倍左右. 当依算法2在此基础上又延长了1.5倍左右.
 |
| 图 6 Olfati算法剩余能量图Fig. 6 Residual energy by Olfati′s algorithm |
 |
| 图 7 本文算法1剩余能量图Fig. 7 Residual energy by our algorithm 1 |
 |
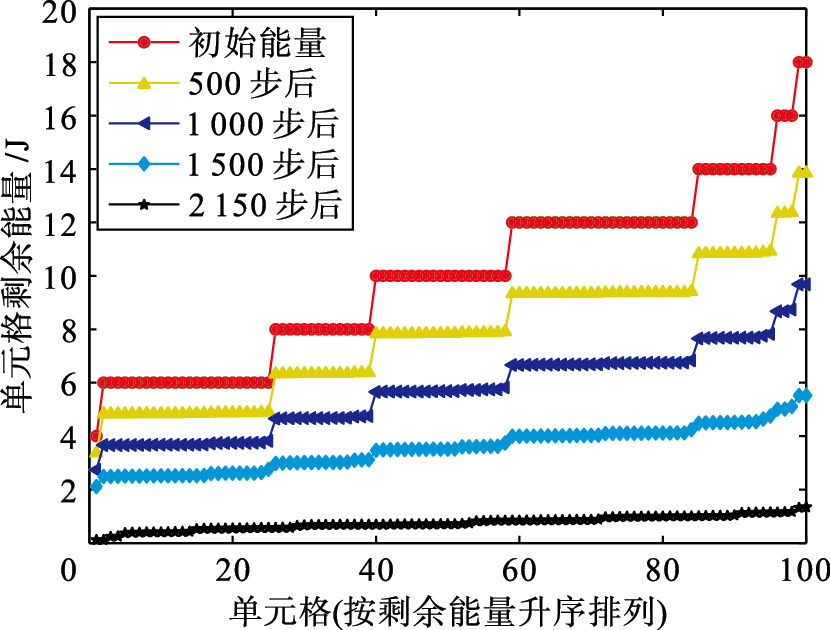| 图 8 本文算法2剩余能量图Fig. 8 Residual energy by our algorithm 2 |
本文提出了一种能量高效的分布式分簇卡尔曼一致性滤波算法对目标系统进行状态估计. 在该算法中： 簇内节点只负责将采集到的目标信息发送给簇头节点，簇头节点融合簇间信息进行预处理，去除了冗余数据，有效地减少了数据传输量. 同时，簇头节点将融合值与其它邻居簇头节点的多份数据进行一致性处理，最终确保所有簇头节点都能精确感知目标信息. 在此基础上，进一步研究了Gossip算法在分布式分簇卡尔曼滤波中的应用. 通过与已有的经典滤波算法进行比较，本文提出的算法具有收敛精度高、 能量消耗少等特点，特别是应用于大规模无线传感器网络时，该算法更能有效地降低节点的能量消耗，大大延长无线传感器网络的生存时间.
| [1] | Olfati-saber R. Distributed Kalman filter with embedded consensus filters[C]//Proceedings of the IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2005: 8179-8184. |
| [2] | Olfati-saber R. Kalman-consensus filter: Optimality, stability and performance[C]//Proceedings of the IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2009: 7032-7046. |
| [3] | Beard R, Casbeer D F. Distributed information filtering using consensus filters[C]//Proceedings of American Control Conference. Piscataway, NJ, USA: IEEE, 2009: 1882-1887. |
| [4] | Olfati-saber R. Distributed Kalman filtering for sensor networks[C]//Proceedings of the 46th IEEE Conference on Decision and Control. Piscataway, NJ, USA IEEE, 2007: 5492-5498. |
| [5] | Ren W, Beard R W, Kingston D B. Multi-agent Kalman consensus with relative uncertainty[C]//Proceedings of American Control Conference. Piscataway, NJ, USA IEEE, 2005: 1865-1870. |
| [6] | 席峰, 刘中. 基于信息矩阵加权一致性策略的分布式Kalman滤波器[J]. 信息与控制, 2010, 39(2): 194-199. Xi F, Liu Z. Distributed Kalman filter with information matrix weighted consensus strategies[J]. Information and Control, 2010, 39(2): 194-199. |
| [7] | 王长城, 戚国庆, 李银伢. 传感器网络一致性分布式滤波算法[J]. 控制理论与应用, 2012, 29(12): 1645-1650. Wang C C, Qi G Q, Li Y Y. Consensus-based distributed filtering algorithm in sensor networks[J]. Control Theory & Applications, 2012, 29(12): 1645-1650. |
| [8] | Heinzelman W, Chandrakasan A, Balakr-ishnan H. Energy-efficient communication protocol for wireless micro-sensor networks[C]//Proceedings of the 33rd Annual Hawaii International Conference on System Science. Piscataway, NJ, USA: IEEE, 2000: 3005-3014. |
| [9] | 李长庚, 谭鹏飞. 一种半径自适应成簇多跳传感器网络路由算法[J]. 信息与控制, 2008, 37(6): 641-646. Li C G, Tan P F. A radius adaptive clustering multi-hop routing algorithm for sensor networks[J]. Information and Control, 2008, 37(6): 641-646. |
| [10] | Younis O, Fahmy S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks[J]. IEEE Transactions on Mobile Computer, 2004, 3(4): 366-379. |
| [11] | 衣晓, 邓露, 刘瑜. 基于基站划分网格的无线传感器网络分簇算法[J]. 控制理论与应用, 2012, 29(2): 145-150. Yi X, Deng L, Liu Y. A clustering algorithm based base station meshing for wireless sensor networks[J]. Control Theory & Applications, 2012, 29(2): 145-150. |
| [12] | Xu Y, Heidemann J, Estrin D. Geography-informed energy conservation for Ad Hoc routing[C]//Proceedings of the 7th Annual International Conference on Mobile Computing and Networking. Piscataway, NJ, USA: IEEE, 2001: 70-84. |
| [13] | Heinzelman W B, Chandra K A, Bala K H. Energy-efficient communication protocol for wireless micro-sensor networks[C]//Proceedings of the 33rd Hawaii International Conference on System Science. Piscataway, NJ, USA: IEEE, 2000: 175-187. |
| [14] | 刘铁流, 巫咏群. 一种新的基于分簇的无线传感器网络多跳节能路由协议[J]. 信息与控制, 2012, 41(1): 27-32. Liu T L, Wu Y Q. A new energy-saving multi-hop routing protocol based on clustering for wireless sensor network[J]. Information and Control, 2012, 41(1): 27-32. |
| [15] | Heinzelman W B, Chandra K A, Bala K H. An application-specific protocol architecture for wireless micro sensor networks[J]. IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670. |
| [16] | Li J Z, Li J B, Shi S F. Concepts, issues and advance of sensor networks and data management of sensor networks[J]. Journal of Software, 2003, 14(10): 1717-1727. |
| [17] | Boyd S, Ghosh A, Prabhakar B, et al. Randomized Gossip algorithms[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2508-2530. |
| [18] | 罗家洪, 方卫东. 矩阵分析引论[M]. 广州: 华南理工大学出版社, 2006. Luo J H, Fang W D. An introduction to the matrix analysis[M]. Guangzhou: South China University of Technology Press, 2006. |
| [19] | Gputa P, Kumar P R. The capacity of wireless networks[J]. IEEE Transactions on Information Theory, 2000, 46(2): 388-404. |
| [20] | Xiao L, Boyd S. Fast linear iterations for distributed averaging[J]. Systems and Control Letters, 2004, 53(1): 65-78. |