2. 计算智能与智能系统北京市重点实验室, 北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligence System, Beijing 100124, China
1 引言
粒子群优化算法(PSO)是Kennedy和Eberhart于1995年提出的一种随机进化算法[1],它源于对鸟群捕食的社会行为的模拟. 由于其算法简单、可调参数少,算法具有本质的并行性、收敛速度快、全局搜索能力强等优点,在解决高维非线性多约束的复杂优化问题上取得了良好的效果;但同时PSO算法也存在一些缺点,如容易陷入局部极值点、搜索后期收敛速度变慢、搜索精度不高、局部搜索能力较差等. 因此,PSO算法展现出较大的潜力和发展空间,已经成为优化领域研究的新亮点.
针对PSO算法的缺点,相关领域的学者对其进行不同方面的改进. Montalvo[2]通过迭代步数调整PSO算法的惯性权重,取得较好效果. Iwasaki[3]为了定量分析算法搜索过程中种群多样性和群体密集程度,提出了种群活动的概念,利用种群活动的反馈机制动态调整权重,有效地平衡了算法的全局和局部搜索能力. Arasomwan[4]基于混沌运动和种群成功率提出了自适应混沌权重调整策略,提高了算法的寻优性能,但算法的稳定性有待加强. Suganthan[5]提出了通过迭代步数线性调整加速系数的方法,展现了比固定值策略更优的性能. Zhan[6]通过集群分析,提出了利用种群中的最好粒子和最差粒子自适应调整两个加速系数,强化了算法搜索能力. Hashemi[7]通过对自动学习机的研究,提出了自动学习调整权重和加速系数的方法,并对比了冒险和保守两个调整策略,结果表明具有学习自动调整的冒险策略效果更佳. Wei[8]利用概率选择法来确定进行局部搜索的粒子,位置越好的粒子进行局部搜索的可能性越大,并取得了较好的效果,但算法鲁棒性需要加强. Tang[9]提出了对全局最优粒子进行局部搜索,通过当前搜索空间大小调整局部搜索的迭代步数,自适应局部搜索,加快算法收敛速度. Sun[10]提出利用黄金比例来确定进行局部搜索的粒子位置,提高了算法寻优能力,但对高维复杂问题效果不是很理想. 施展[11]提出的ε优势支配,构建了一类多目标量子行为粒子群优化算法,能够更好维护粒子分布的均匀性和宽广性,增加了种群多样性,并分析了算法在粒子位置有界的条件下能达到全局收敛.
PSO算法中对参数值的设定决定算法优化性能,为了充分利用种群迭代过程中的内部信息动态调整算法参数及增强算法局部搜索能力,本文提出一种具有局部搜索的自适应粒子群算法(adaptive particle swarm optimization algorithm with local search,LSAPSO),在函数优化中显示出了良好的优化性能. 将LSAPSO算法用于汉诺塔管网、纽约管网的优化设计中,同样取得了良好的效果.
2 粒子群算法 2.1 基本PSO算法PSO算法结合了生命科学和优化计算的优点,群体中的个体代表问题的一个潜在解,迁移相当于迭代,食源相当于全局最优解. 若优化问题的搜索空间是n维的,则第i个粒子的位置和速度用数学方式可分别表示为Xi=(xi1,xi2,…,xin),Vi=(vi1,vi2,…,vin). 粒子根据速度和位置公式迭代,更新公式为


PSO算法存在的主要问题是容易陷入局部极值点,影响算法性能,而算法参数ω、c1、c2的值对算法的优化性能起着决定性影响,因此对算法参数的调整成为PSO算法研究的热点领域:根据经验设定PSO算法参数,应用最为广泛的是固定值调整策略[2]. 通过迭代步数对ω进行非线性调整[12]:
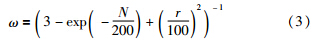
Cheng[13]通过分析粒子的位置多样性和认识多样性,提出粒子距离范围内最优粒子比例,进而调整惯性权重,其公式为
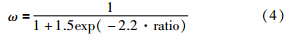

文[5]提出通过迭代步数线性调整加速系数c1、c2:

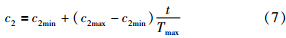
Kinoshita[14]通过分析种群多样性,提出每个粒子与最优粒子的欧氏距离,并利用种群信息动态调整加速系数:
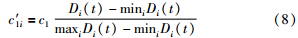

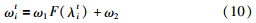

粒子群算法迭代后期收敛速度变慢,局部寻优能力较差,搜索精度不高. 针对此问题,刘朝华[16]提出将群体划分为正向和反向学习模态的小波粒子群算法,提高了算法的动态局部寻优性能. Ding[17]提出采用局部随机搜索来调整惯性权重,平衡了算法全局和局部搜索能力,提高了算法的寻优性能. Xia[18]提出利用混沌和轮盘赌原理进行局部搜索,提高了算法局部搜索性能和搜索精度,混沌变量cxik的计算公式为
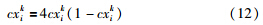
通过轮盘赌算法原理选定进行局部搜索的粒子xik+1:
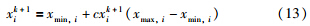
文[10]提出利用黄金比例确定进行局部搜索的粒子,为了减少不同维度范围不同带来的影响,将优化问题的变量间隔映射到[-1,1]之间:
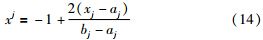
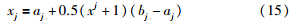
从上述关于PSO参数调整和局部搜索的分析可知,以上PSO算法的改进都在不同程度上提高了算法的优化性能,但没有充分利用迭代过程中的种群内部信息. 本文在种群分布信息的基础上提出了趋同因子的概念,使其能够在统一机制下根据当前种群分布状态自适应调整算法的3个参数,并对其进行自适应局部搜索,利用种群内部信息得到该粒子变异的可能性大小,对其进行自适应混沌变异.
3 自适应粒子群算法通过实际问题进行数学建模形成高维非线性函数会有很多局部极小或极大值,表现为波谷或波峰,在用粒子群算法优化时容易陷入局部极值,出现早熟现象,为定量描述粒子分布,提出趋同因子st:
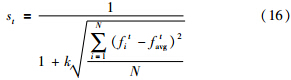

粒子群算法在迭代初期,种群的随机初始化会导致离散程度较大,适应度值差别较大,此时趋同度st较小,趋近于0;迭代后期粒子在全局最优粒子的引领下逐渐趋向某一点,此时趋同度st较大,趋近于1.
3.1 参数自适应调整策略优化算法通常基于一定的规则来调整参数,从不同角度出发会得到不同的规则. 自适应调整规则是根据历史迭代信息动态来调整参数,通过不断调整达到寻优效果. 由上述分析可见,参数调整对算法性能有决定性的影响. 本文从趋同因子思想出发,提出了参数调整函数P(sit):
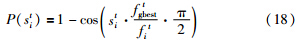
ω是PSO中重要的参数,用来控制算法的开发和探索能力. 算法迭代初期ω应较大,以增强算法的全局搜索能力;后期应减小,以增强算法的局部探索能力. 本文根据惯性权重的调整思想,提出了ω的更新公式:

加速系数c1称为个体认知,c2称为社会认知,在算法搜索初期,应c1较大、c2较小,以增加种群的多样性,便于搜索优化问题整个解空间;算法搜索后期,应减小c1、增大c2,加快算法的收敛速度. 根据加速系数的调整思想,提出c1、c2的更新公式:
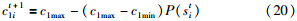

PSO算法是一种全局搜索算法,在进化后期搜索精度不高、收敛速度变慢,为此在PSO算法中加入一种局部搜索机制,与全局搜索算法相比,规模会减小.
(1) 参加局部搜索的粒子个数减少. 全局搜索中每个粒子都参与搜索过程,局部搜索时对每个粒子设置一个是否进行局部搜索的判断条件:

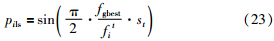
第t次迭代时7种群趋同度st越大,第i个粒子适应度值fit与全局最优值fgbest越接近,自适应局部搜索概率pils也就越大;反之,可能性就越小.
(2) 搜索范围减小. 对个体极值而言,在当前位置的每一维分量添加一个随机数r1∈(-α,α):


对全局极值而言,在当前位置的每一维分量添加一个随机数r2∈(-β,β):

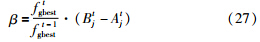
(3) 迭代步数减少. 局部搜索迭代步数与全局搜索相比要少很多,整体呈现逐渐增加的趋势,具体设置方法为定义最大迭代步数Tmax,并把整个迭代过程分为5个阶段,每个阶段分别以最大迭代步数的2%、4%、6%、8%、10%次迭代进行局部搜索.
3.3 种群自适应变异策略为避免算法陷入局部最优,本文引入混沌机制,利用混沌变量遍历性的特点,更有效地带领粒子群移向最优解. 通过种群中的每个粒子趋同度和适应度值的大小,对每个粒子设置一个变异概率,如式(28)所示,若满足变异条件式(29),对该粒子进行混沌变异:
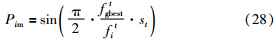

当种群聚集程度越大时,趋同度st也越大,pim就越大,个体适应度值越趋近全局极值,此时对粒子进行变异,能够跳出局部极值;反之,当种群分布分散时,算法不易陷入局部最优. 若满足变异条件则按式(30)进行混沌变异,变异后粒子的新位置为x′ij,如式(31)所示:
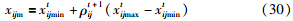

本文从种群分布状态的角度出发,提出基于局部搜索的自适应变异粒子群算法(LSAPSO),对参数自适应调整策略、局部自适应搜索策略和变异策略进行了设计. 该算法的具体实现过程如下:
Step 1:算法初始化:设定种群规模为N,惯性权重ω的上下界为ωmax、ωmin,加速系数为c1max、c1min、c2max、c2min,最大迭代步数为Tmax.
Step 2:种群初始化:设初始迭代步数t=1,并随机初始化位置向量xi.
Step 3:根据式(19)~式(21)更新ω、c1、c2.
Step 4:根据式(1)、式(2)更新位置x、速度v.
Step 5:粒子适应度评价:计算每个粒子的适应度值fi,并更新Pbestit、Gbestt.
Step 6:根据式(17)、式(18)计算出参数调整函数p(sit),并以次为基础分别根据式(23)、式(28)得到局部搜索概率pils和变异概率pim.
Step 7:对每个粒子执行如下变异操作:
1) 判断粒子是否满足变异条件. 若满足,则根据式(30)、(31)进行混沌变异,并重新计算粒子的适应度值.
2) 若变异后粒子适应度值优于当前的个体极值,则将Pbestit更新为该变异值.
3) 同理,更新全局极值Gbestj.
Step 8:对个体极值、全局极值执行局部搜索操作:
1) 分析局部搜索条件. 若满足,计算α、β.
2) 对个体极值,根据式(24)进行局部搜索,更新个体极值和全局极值.
3) 对全局极值,根据式(26)进行局部搜索,并更新全局极值.
Step 9:判断算法是否满足终止条件. 若满足,则算法结束,输出Gbest即为最优结果;若不满足,则t=t+1,转至Step 3.
4 实验分析 4.1 LSAPSO算法性能测试为了验证文中提出的LSAPSO算法性能,通过6个Benchmarks函数进行测试,以上函数最优值或位于抛物线形峡谷内,或为多峰函数,最优值附近有大量局部极小值,具有代表性,各测试函数描述见表 1.
各个算法采用相同的初始化种群数300,缩放因子线性递减差分算法(DE-TVSF)、缩放因子随机分布差分算法(DE-RSF)参数设置参照文[19],权重线性递减粒子群算法(LDWPSO)参数设置参照文[7],LSAPSO算法参数ω的范围为[0.4,0.9],c1和c2的范围为[0.5,2.5],调整因子k=0.1. 各算法均运行20次,最大迭代步数为1 000,仿真结果见表 2,在上述测试实验中随机抽取一组实验结果画图进行对比. 为便于对比,取函数值的对数为纵坐标,迭代步数为横坐标,测试函数优化收敛曲线见图 1~6.
| 函数 | 维数 | 平均解(标准差) | 成功率(平均迭代步数) | ||||||
| DE-TVSF | DE-RSF | LDWPSO | LSAPSO | DE-TVSF | DE-RSF | LDWPSO | LSAPSO | ||
| f1 | 30 | 0.001 | 0.001 | 0.001 | 0.001 | 100%(802) | 100%(912) | 100%(586) | 100%(530) |
| f2 | 30 | 1.41e-01(2.224e-001) | 7.38e-01(1.442e-001) | 6.25e-01(3.426e-002) | 1.02e-01(1.258e-004) | 10%(7615) | 25%(5710) | 80%(284) | 100%(116) |
| f3 | 30 | 2.6e-003(1.12e-001) | 5.8e-003(2.77e-001) | 5.723e-002(2.264e-001) | 2.158e-003(3.482e-002) | 100%(1721) | 95%(1934) | 90%(703) | 100%(685) |
| f4 | 30 | 2.6e-003(3.5e-003) | 1.9e-002(2.2e-002) | 6.286e-003(1.22e-002) | 1.68e-005(1.8e-003) | 95%(627) | 85%(574) | 95%(348) | 100%(325) |
| f5 | 30 | 4.86e-001(2.278e+000) | 4.27e-001(1.582e+000) | 2.508e-001(2.809e+000) | 1.24e-002(1.856e-001) | 70%(1594) | 70%(1905) | 80%(1298) | 95%(1150) |
| f6 | 30 | 4.45e-002(6.9e-002) | 1.1e-003(8.8e-002) | 1.718e-002(1.431e-001) | 2.145e-005(4.068e-004) | 85%(814) | 90%(896) | 70%(602) | 100%(598) |
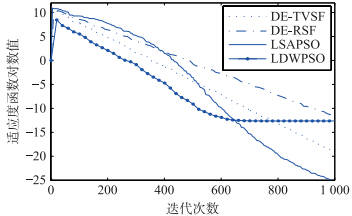 |
| 图 1 函数f1收敛曲线Fig. 1 The convergence curves of function f1 |
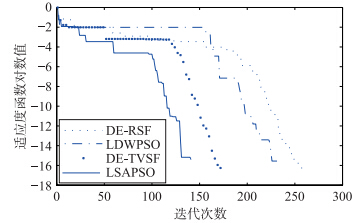 |
| 图 2 函数f2收敛曲线Fig. 2 The convergence curves of function f2 |
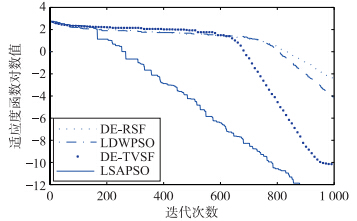 |
| 图 3 函数f3收敛曲线Fig. 3 The convergence curves of function f3 |
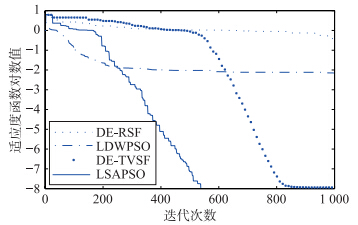 |
| 图 4 函数f4收敛曲线Fig. 4 The convergence curves of function f4 |
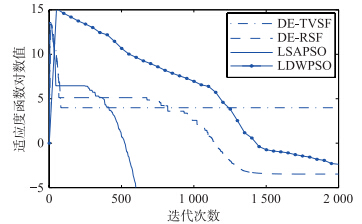 |
| 图 5 函数f5收敛曲线Fig. 5 The convergence curves of function f5 |
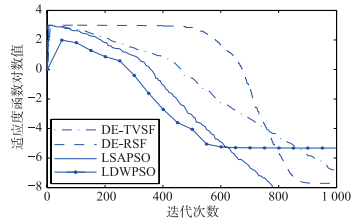 |
| 图 6 函数f6收敛曲线Fig. 6 The convergence curves of function f6 |
对比表 2中解的平均值和标准差(无括号部分表示标准差为0)可见,LSAPSO算法有更好的搜索精度且算法鲁棒性更高. 表 2中的算法搜索成功率及其迭代步数的实验数据表明,LSAPSO算法在保证成功率的基础上具有更快的收敛速度. 图 1~图 6表明:相比于其它3种算法,LSAPSO算法具有更好的求解质量且收敛速度更快.
4.2 实例应用及结果分析通过优化6个高维的基准函数,证明了LSAPSO算法的优化性能,下面将其用来优化2个实际的管网案例:第1个管网案例是汉诺塔管网,其布局见图 7,管网详细数据、目标函数和约束条件参照文[20]. 汉诺塔管网有6种标准离散管径可供选择,各管径单位长度造价见表 3. 第2个管网案例是纽约管网,其布局见图 8,管网详细数据、目标函数和约束条件参照文[20],可供选择的新管段共有16种,表 4列出了新管段单位长度的造价值.
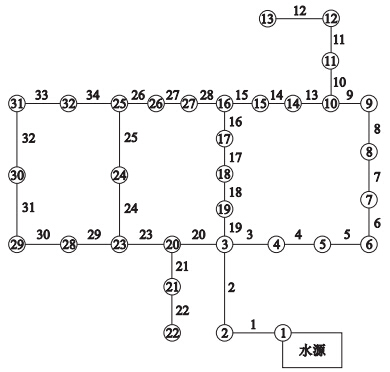 |
| 图 7 汉诺塔管网布局图Fig. 7 Layout of Hanoi network |
| 管段编号 | 管径/mm | 造价/(美元/m) |
| 1 | 304.8 | 45.762 |
| 2 | 406.4 | 70.400 |
| 3 | 508.0 | 98.378 |
| 4 | 609.6 | 129.333 |
| 5 | 762.0 | 180.748 |
| 6 | 1 016.0 | 278.280 |
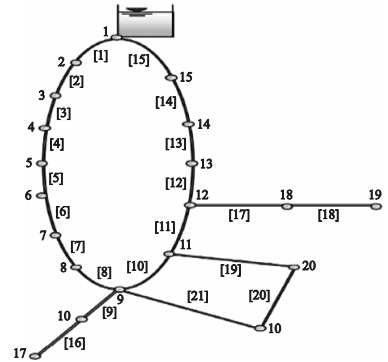 |
| 图 8 纽约管网布局图Fig. 8 Layout of the New York tunnels network |
| 管段编号 | 管径/cm | 造价/(美元/m) |
| 1 | 0 | 0 |
| 2 | 91.44 | 306.76 |
| 3 | 121.92 | 439.63 |
| 4 | 152.40 | 577.43 |
| 5 | 182.88 | 725.07 |
| 6 | 213.36 | 875.98 |
| 7 | 243.84 | 1 036.75 |
| 8 | 274.32 | 1 197.51 |
| 9 | 304.80 | 1 368.11 |
| 10 | 335.28 | 1 538.71 |
| 11 | 365.76 | 1 712.60 |
| 12 | 396.24 | 1 893.04 |
| 13 | 426.72 | 2 073.50 |
| 14 | 457.20 | 2 260.50 |
| 15 | 487.68 | 2 447.51 |
| 16 | 518.16 | 2 637.80 |
LSAPSO算法优化汉诺塔管网时,经过参数敏感性分析,各参数设置如下:种群规模N=300,海曾—威廉系数C=130,ωmax=0.9,ωmin=0.4,c1max=2.5,c1min=0.5,c2max=2.5,c2min=0.5,参数调整因子k=0.1,算法运行100次. 图 9给出最优工程造价的收敛曲线,随着迭代进行适应度值逐渐减小并找到了目前最优的工程造价6.081×106美元.
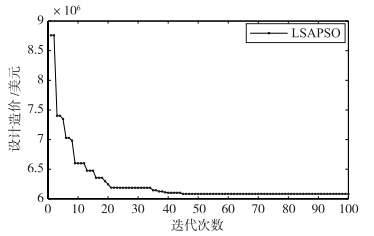 |
| 图 9 汉诺塔管网造价收敛曲线Fig. 9 The cost convergence curve for Hanoi network |
表 5中自适应粒子群(APSO)算法优化结果参照文[2],遗传算法(GA)、基于最优个体为基向量改进的差分算法(DE/best/2/bin,DE2)、蛙跳算法(SFLA)结果参照文[20],其中GA、DE2、APSO和本文提出的LSAPSO算法都找到了目前最优的工程造价,经过EPANET 2.0验证满足水力约束条件,而本文提出的LSAPSO算法仅对目标函数进行了34 800次评价,且具有较高的搜索成功率,说明改进的算法稳定性好、全局寻优能力较强,在解决给水管网这类组合优化问题时具有较大的优势.
| 算法 | 造价 /美元 | 迭代次数 | 成功率 |
| GA | 6 081 087 | 74 500 | - |
| APSO | 6 081 087 | 65 200 | 92 |
| DE2 | 6 081 087 | 48 724 | 82 |
| SFLA | 6 117 000 | 15 955 | - |
| LSAPSO | 6 081 087 | 34 800 | 95 |
对于纽约管网模型优化,经过参数敏感性分析,LSAPSO算法中参数设置如下:种群规模N=120,其它参数与汉诺塔管网中参数设置相同,算法最大迭代步数Tmax=100. 水力计算中海曾—威廉系数C=100. 图 10是纽约管网造价收敛曲线,算法在迭代到第21步时就找到全局最优值38.52×106美元,也是目前经过EPANET 2.0水力计算后均满足约束条件的最优工程造价.
 |
| 图 10 纽约管网造价收敛曲线Fig. 10 The cost convergence curve for New York network |
表 6中管道编号对应的直径单位是cm,造价单位是美元,APSO算法结果参照文[2],粒子群与差分混合算法(PSO-DE)结果参照文[5],GA、HGA结果参照文[21],其中GA得到37.13×106美元的造价,使用EPANET 2.0进行水力计算后,节点16、17和19的水头压力并不满足最小节点服务水头,方案不可行. HGA得到38.13×106美元的造价,此方案允许节点水压扬程有1.5 cm的误差,该方案仍不可行. PSO-DE算法与本文提出的LSAPSO算法均得到造价为38.52×106美元的方案,经过EPANET 2.0计算都满足约束条件,而PSO-DE算法是在第26步找到的全局最优值,本文提出的LSAPSO算法在第21步就找到了全局最优值.
| 管段编号 | GA | HGA | PSO-DE | APSO | LSAPSO |
| 7 | 274.32 | 335.28 | 0 | 365.76 | 0 |
| 15 | 0 | 0 | 243.84 | 0 | 243.84 |
| 16 | 213.36 | 243.84 | 243.84 | 243.84 | 243.84 |
| 17 | 243.84 | 243.84 | 243.84 | 243.84 | 243.84 |
| 18 | 213.36 | 213.36 | 213.36 | 213.36 | 213.36 |
| 19 | 182.88 | 182.88 | 182.88 | 182.88 | 182.88 |
| 21 | 182.88 | 182.88 | 182.88 | 182.88 | 182.88 |
| 成本/×106美元 | 37.13 | 38.13 | 38.52 | 38.64 | 38.52 |
针对粒子群算法容易陷入局部最优、搜索精度不高的问题,为充分利用种群迭代的分布信息,本文提出了趋同因子的概念,在此基础上设置参数调整函数来自适应调整ω、c1和c2;在算法中加入一种局部搜索机制,对全局极值和个体极值进行局部搜索;为了增加种群多样性对其进行混沌变异,增强了算法的寻优能力. 通过6个标准函数进行测试,仿真结果表明该算法具有更好的全局和局部搜索能力,且具有更快的收敛速度. 以给水管网优化为研究背景,将其用来优化两个实际的管网案例——汉诺塔管网、纽约管网,LSAPSO算法经过较少的进化次数就找到全局最优解,且搜索成功率和搜索精度较高,能以最小的计算代价找到全局最优方案. 未来研究工作将重点关注种群动态分布信息的评价标准,以此来增强算法的寻优性能.
| [1] | Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceedings of the International Conference on Neural Network. Piscataway, NJ, USA: IEEE, 1995: 1942-1948. |
| [2] | Montalvo I, Izquierdo J, Pérez-Garcia R, et al. Improved performance of PSO with self-adaptive parameters for computing the optimal design of water supply systems[J]. Engineering Applications of Artificial Intelligence, 2010, 23(5): 727-735. |
| [3] | Iwasaki N, Yasuda K, Ueno G. Particle swarm optimization: Dynamic parameter adjustment using swarm activity[C]//2008 IEEE International Conference on Systems, Man and Cybernetics. Piscataway, NJ, USA: IEEE, 2008: 2634-2639. |
| [4] | Arasomwan M A, Adewumi A O. On adaptive chaotic inertia weights in particle swarm optimization[C]//2013 IEEE Symposium on Swarm Intelligence. Piscataway, NJ, USA: IEEE, 2013: 72-79. |
| [5] | Suganthan P N. Particle swarm optimiser with neighbourhood operator[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE: 1958-1965. |
| [6] | Zhan Z H, Xiao J, Zhang J, et al. Adaptive control of acceleration coefficients for particle swarm optimization based on clustering analysis[C]//IEEE Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2007: 3276-3282. |
| [7] | Hashemi A B, Meybodi M R. A note on the learning automata based algorithms for adaptive parameter selection in PSO[J]. Applied Soft Computing, 2011, 11(1): 689-705. |
| [8] | Wei J X, Jia L P. A novel particle swarm optimization algorithm with local search for dynamic constrained multi-objective optimization problems[C]//IEEE Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2013: 2436-2443. |
| [9] | Tang J, Zhao X J. Particle swarm optimization using adaptive local search[C]//Proceedings of the International Conference on Future Biomedical Information Engineering. Piscataway, NJ, USA: IEEE, 2009: 300-303. |
| [10] | Sun Y X, Wyk B J, Wang Z H. A new golden ratio local search based particle swarm optimization[C]//International Conference on Systems and Informatics. Piscataway, NJ, USA: IEEE, 2012: 754-757. |
| [11] | 施展, 陈庆伟, 胡维礼. 一类多目标量子行为粒子群优化算法收敛性分析及应用[J]. 信息与控制, 2013, 42(4): 407-415. Shi Z, Chen Q W, Hu W L. Convergence analysis of a class of multi-objective quantum-behaved particle swarm optimization algorithms and its application[J]. Information and Control, 2013, 42(4): 407-415. |
| [12] | Mahor A, Rangnekar S. Short term generation scheduling of cascaded hydro electric system using novel self adaptive inertia weight PSO[J]. International Journal of Electrical Power & Energy Systems, 2012, 34(1): 1-9. |
| [13] | Shi C, Shi Y H, Quande Q, et al. Population diversity based inertia weight adaptation in particle swarm optimization[C]//IEEE Fifth International Conference on Advanced Computational Intelligence. Piscataway, NJ, USA: IEEE, 2012: 395-403. |
| [14] | Kinoshita K, Watanabe K, Isshiki M. Estimation of inverse model based on ANN and PSO with adaptively varying acceleration coefficients[C]//Proceedings of the 2014 IEEE SICE Annual Conference (SICE). Piscataway, NJ, USA: IEEE, 2014: 281-286. |
| [15] | Wu Z, Zhou J. A self-adaptive particle swarm optimization algorithm with individual coefficients adjustment[C]//2007 International Conference on Computational Intelligence and Security. Piscataway, NJ, USA: IEEE, 2007: 133-136. |
| [16] | 刘朝华, 周少武, 刘侃. 基于双模态自适应小波粒子群的永磁同步电机多参数识别和温度检测方法[J]. 自动化学报, 2013, 39(12): 2121-2130. Liu C H, Zhou S W, Liu K. Permanent motor multiple parameter identification and temperature monitoring based on wavelet particle swarm optimization[J]. Acta Automatica Sinica, 2013, 39(12): 2121-2130. |
| [17] | Ding J L, Liu J, Chowdhury K R, et al. A particle swarm optimization using local stochastic search and enhancing diversity for continuous optimization[J]. Neurocomputing, 2014, 137(5): 261-267. |
| [18] | Xia X. Particle swarm optimization method based on chaotic local search and roulette wheel mechanism[C]//Proaedings of the International Conference on Applied Physics and Industrial Engineering. Amesterda, Holland: Elsevier, 2012: 269-275. |
| [19] | Das S, Konar A, Chakraborty U K. Two improved differential evolution schemes for faster global search[C]//Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. New York, NJ, USA: ACM, 2005: 991-998. |
| [20] | Sedki A, Ouazar D. Hybrid particle swarm optimization and differential evolution for optimal design of water distribution systems[J]. Advanced Engineering Informatics, 2012, 26(3): 1-10. |
| [21] | Muzaffar M, Kevin E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Journal of Water Resources Planning and Management, 2003, 129(3): 210-225. |




