2. 河南理工大学数信学院, 河南 焦作 454003
2. School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo 454003, China
1 引言
微分博弈理论是控制论和博弈论的重要分支,它起源于军事,但不局限于军事,目前已被广泛应用于社会、经济、政治等生活的各个方面. 随着研究的不断加深,微分博弈的应用前景将会更加宽广. 微分博弈是指参与人的行动有先后顺序,而且行动在后者可以观察到行动在先者的选择,并据此作出相应的选择. 它是处理双方或多方动态冲突、竞争或合作问题的一种有效工具. 微分博弈的困难在于,在前一刻最优的决策在下一刻可能不再为最优,因此在求解上存在很大的困难.
简单来讲,微分博弈就是在局中人进行博弈活动时,要用到微分方程(组)来描述对象或规律的一种博弈,是一种双(多)方的最优控制问题,它将现代控制理论与博弈论相融合,从而比控制理论具有更强的竞争性和对抗性.
考虑追捕逃逸型微分博弈问题:
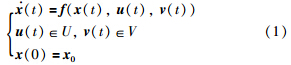
关于追捕逃逸型微分博弈问题已有一些研究成果. 文[1, 2]给出了微分博弈问题的无忧先规则的位置策略,并证明了选择定理. 文[3]推广了解的定义,给出了近似微分博弈,使用了非期望策略(nonanticipative strategies),这样局中人就可以通过对方行动信息来决定自己的行动. 文[3]的另一个重要贡献就是通过几何方式研究了胜利域(victory domain). 随后,文[4]对胜利域做了数值计算. 文[5]描述了具有状态约束的追捕逃逸型问题,证明了微分博弈值的存在性;文[6]将这一理论推广到混杂系统. 文[7]主要的贡献是结合凸可行问题的算法给出该问题的投影算法. 在文[8]中,作者利用Hamilton-Jacobi方程的粘性解求出此问题的生存核;在这一算法过程,作者利用微分包含来表示微分博弈,本质上就是用微分博弈理论来求解微分包含问题.
在实际应用中,微分博弈识别域的判别是至关重要的,因为它关系着局中人胜利域及捕获域、逃逸域的表示. 而胜利域、捕获域和逃逸域是追捕逃逸型微分博弈中最基本和最重要的概念,胜利域、捕获域和逃逸域的确定和计算是博弈理论中的核心问题,这个问题正是目前微分博弈问题中需要解决的关键问题,这些问题的有效解决必将会对微分博弈的研究和发展起到重要推动作用. 然而,正如一般非线性系统生存域的判别定理很难具体被使用一样,目前关于微分博弈问题识别域的判别还没有切实可行的判别准则. 因此,本文将要研究一类特定的非线性控制系统即仿射非线性系统下的追捕逃逸型微分博弈问题,利用生存域的判别方法,最终给出该问题识别域类似KKT条件的判别方法.
2 基本概念与性质本节简单地介绍一下识别域的基本概念和性质.
定义1 设闭集S⊂Rn,x∈S,如果dS(x+p)=‖p‖,其中dS(y)为点y到集合S的距离,即dS(y)=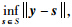 则称向量p∈Rn为集合S在x处的近似法向量,所有p的集合记为NPS(x).
则称向量p∈Rn为集合S在x处的近似法向量,所有p的集合记为NPS(x).
定义2 如果对任意的x∈S和p∈NPS(x),有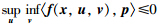 成立,则称S为f(x)的识别域. S所包含的f(x)的最大识别域称为f(x)的识别核,记为Discf(S).
成立,则称S为f(x)的识别域. S所包含的f(x)的最大识别域称为f(x)的识别核,记为Discf(S).
定义3 如果对任意的x∈S和p∈NPS(x),有 成立,则称S为f(x)的领导域. S所包含的f(x)的最大领导域称为f(x)的领导核,记为Leadf(S).
成立,则称S为f(x)的领导域. S所包含的f(x)的最大领导域称为f(x)的领导核,记为Leadf(S).
定义4 设K⊂Rn非空,集合K在点x∈K处的切锥定义为
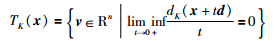
事实上,v∈TK(x)当且仅当存在hk>0,vk∈Rn,k=1,2,…,时且满足hk→0,vk→v,使得x+hkvk∈K,∀k≥0[9].
定义5 记时间测度控制集为
 ={u(t)|u(t)是[0,+∞)到U上的可测函数}
={u(t)|u(t)是[0,+∞)到U上的可测函数}
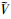 ={v(t)|v(t)是[0,+∞)到V上的可测函数}
={v(t)|v(t)是[0,+∞)到V上的可测函数}
定义映射α: →
→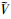 ,如果满足下面的条件,则映射α称为局中人1的一个非期望策略:对于任意的s≥0和任意的v1(t),v2(t)∈
,如果满足下面的条件,则映射α称为局中人1的一个非期望策略:对于任意的s≥0和任意的v1(t),v2(t)∈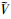 ,如果v1(t)和v2(t)在[0,s]上几乎处处一致,则α(v1(t))和α(v2(t))在[0,s]上几乎处处一致.
,如果v1(t)和v2(t)在[0,s]上几乎处处一致,则α(v1(t))和α(v2(t))在[0,s]上几乎处处一致.
同样,可以定义局中人2的一个非期望策略β: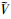 →
→ ,不再赘述.
,不再赘述.
定义6 设存在一个非期望策略α: →
→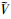 和正数ε、T,对于局中人2的任意的v(t)∈
和正数ε、T,对于局中人2的任意的v(t)∈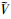 ,解x(x0,α(v(t)),v(t))都能在t<T时到达Ωε={x|dΩ(x)≥ε},满足这些条件的初始值x0∉Ω的集合称为局中人1的胜利域.
,解x(x0,α(v(t)),v(t))都能在t<T时到达Ωε={x|dΩ(x)≥ε},满足这些条件的初始值x0∉Ω的集合称为局中人1的胜利域.
设存在一个非期望策略β: →
→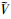 ,对于局中人1的任意的u(t)∈
,对于局中人1的任意的u(t)∈ ,解x(x0,u(t),β(u(t)))都能在t≥0时避开Ω,满足这些条件的初始值x0∉Ω的集合称为局中人2的胜利域.
,解x(x0,u(t),β(u(t)))都能在t≥0时避开Ω,满足这些条件的初始值x0∉Ω的集合称为局中人2的胜利域.
假设1
(1) f(x,u,v)为连续函数;
(2) 对任意的u∈U,v∈V,f(·,u,v)为Lipschitz函数.
假设1中的两个条件在约束优化最优性条件研究中广为使用,通常的集合都会满足这两个假设条件.
引理1 如果假设1成立,令S=Rn\Ω,则:
(1) 局中人1的胜利域是S\Discf(S);
(2) 局中人2的胜利域是Discf(S).
引理1表明了胜利域与识别核的关系,而识别核又是最大的识别域,为了判别胜利域,就必须先判别识别域,所以下面来讨论识别域的判别方法.
3 识别域判别方法在实际应用中,大多数问题都是仿射非线性的,所以考虑如下仿射非线性问题:
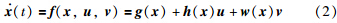
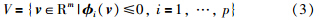
仿射非线性系统是一种特定的非线性系统,它对控制是线性的. 在实际应用中,经常会遇到一些多变量非线性复杂系统,其数学模型必然是非线性微分方程(组),经过适当变换,大部分可以写成仿射非线性系统(2)[10],所以本文研究仿射非线性系统(2)是有理论依据和实际意义的. 本节将研究仿射非线性系统(2)在光滑区域和非光滑区域上识别域的判别问题.
3.1 关于光滑区域的识别域考虑如下区域:

给定x∈W,定义指标集:
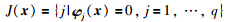
如果J(x)为空集,则x为W的内点. 因为判别识别域只需要考虑边界点,所以只需考虑指标集J(x)非空的情况即可. 给出集合W在点x∈W处的约束品性.
约束品性1[11] 存在y0∈Rn,使得∇φTj(x)y0<0,j=1,…,q.
约束品性2[11] clγ(x)=Γ(x)成立,其中cl为闭包,

上述两个约束品性在约束优化最优性条件研究中广为使用,通常的集合都会满足这些假设.
命题1[11] 如果集合W在x∈Rn处满足约束品性1或约束品性2,则有TW(x)=Γ(x).
命题2[9] 如果假设1成立,闭集W是识别域的充要条件是对任意x∈W,任意u∈U有:

对于集合W的内点x,有TW(x)=Rn,这时式(5)总成立. 于是,要判别式(5),只需考虑边界点即可.
命题3[12] 在假设1和约束品性1或约束品性2成立的情况下,W是f(x)识别域的充要条件是对每一个固定的x∈Rn和u∈U,下列不等式组有解:
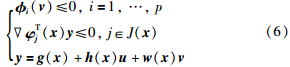
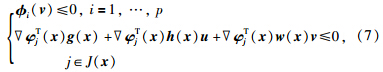
命题4(Gordan引理) 设A1,A2,…,Al是l个n维向量,不存在向量P使
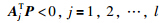
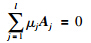
一个命题的等价命题一定是成立的,下面将利用Gordan引理的等价命题来给出不等式组(7)的解的情况.
定理1 不等式组(7)有解的充要条件是存在非零实数μi(i=1,2,…,p)和μj(j=1,2,…,q),使
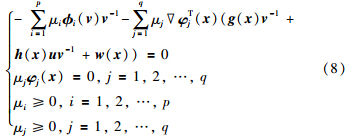
证明 首先本文给出Gordan引理的等价命题:
设A1,A2,…,Al是l个n维向量,存在向量P使
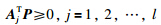
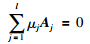
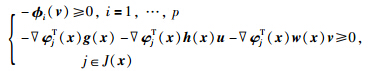
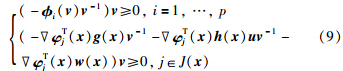
对式(9)利用Gordan引理的逆否命题: 存在不全为零的非负实数
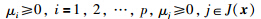
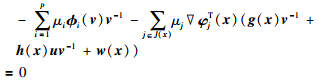
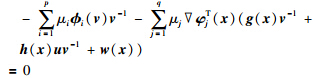
注1 定理1说明对于光滑区域W和仿射非线性系统(2)~(3),识别域条件(5)成立可转化成对每个固定的x∈W,方程组(8)有解问题.
注2 考虑一般非线性追捕逃逸型微分博弈问题(1),其中V和W根据式(3)和式(4)计算,只需把不等式组(6)变成:
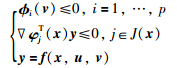
类似于上面定理的推导方式,最终可以得到类似(8)的如下方程组:

例 考虑仿射非线性系统:

令U={(u1,u2)∈R2|u21+u22≤1},V={(v1,v2)∈R2|v21+v22≤1},考虑集合W={(x1,x2)∈R2|x21+x22≤1}. 下面判别集合W在点(0,1)T处是否满足识别域条件,为此记:
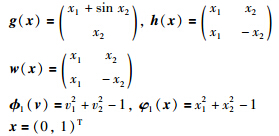
显然J(x)={1}. 将上面的式子代入方程组(8),不难验证该方程组有解,故集合W关于仿射非线性系统(10)在x=(0,1)T处满足识别域条件.
3.2 关于非光滑区域的识别域考虑如下区域:
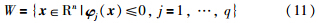
定义7[11] 设g(x)为Rn上的方向可微函数,如果存在凸紧集∂g(x)∈Rn使得其方向导数可表示为
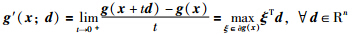
次微分有很多种,本文中用到的次微分为Clarke次微分,下面给出Clarke次微分的定义:
定义8[14] 设f(x)为Rn上的局部Lipschitz函数,Df是f(x)可微的点集,则x处的Clarke次微分为
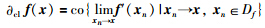
约束品性3 存在y0∈Rn,使得φ′j(x;y0)<0,j=1,…,q.
约束品性4 clγ(x)=Γ(x)成立,其中cl为闭包,
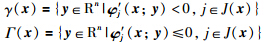
上述两个约束品性在约束优化最优性条件研究中广为使用,通常的集合都会满足这些假设.
命题5[11] 如果集合W在x∈Rn处满足约束品性3或约束品性4,则有TW(x)=Γ(x).
命题6[15] 在假设1和约束品性3或约束品性4成立的情况下,则W是f(x)识别域的充要条件是对每一个固定的x∈Rn和u∈U,下列不等式组有解:
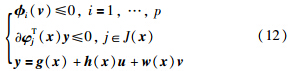
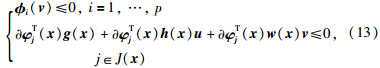
定理2 不等式组(13)有解的充要条件是存在非零实数μi(i=1,2,…,p)和μj(j=1,2,…,q),使

证明 首先给出Gordan引理的等价命题:
设A1,A2,…,Al是l个n维向量,存在向量P使
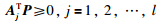
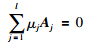

进而有:
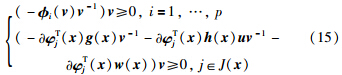
对式(15)利用Gordan引理的等价命题:存在不全为零的非负实数μi≥0(i=1,2,…,p),μj≥0(j∈J(x)),使
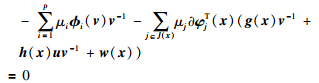
当j∉J(x)时,取对应的μj=0,从而上式变为

注3 定理2说明对于非光滑区域W和仿射非线性系统(2)、(3),识别域条件(5)成立可转化成对每个固定的x∈W,方程组(14)有解的问题.
注4 考虑一般非线性追捕逃逸型微分博弈问题(1),其中V和W根据式(3)和式(11)计算,则只需把不等式组(13)变成:
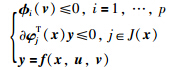
类似于上面定理的推导方式,最终可以得到类似式(14)的方程组:
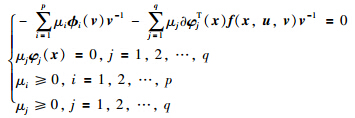
本文研究了追捕逃逸型微分博弈关于由不等式表示的光滑区域和非光滑区域的识别域判别问题. 对于光滑区域的判别,利用Gordan引理的等价命题,推出了仿射非线性系统的类似KKT条件的识别域判别方法及一般非线性系统识别域的判别方法. 对于非光滑区域的判别,利用了方向倒数和次微分,这里次微分本文采用的是Clarke次微分,Clarke次微分是传统次微分的一般化形式,同样推导出仿射非线性系统类似KKT条件的识别域判别方法和一般非线性系统识别域的判别方法. 进而就可以利用引理1来写出系统的胜利域.
| [1] | Krasovskii N N, Subbotin A I. Game theoretical control problems[M]. Berlin, Germany: Springer-Verlag, 1988. |
| [2] | Krasovskii N N, Subbotin A I. Universal optimal strategies in positional differential games[J]. Differential Equation, 1984, 19(11): 1377-1382. |
| [3] | Cardallaguet P. Differential game with two players and one target[J]. SIAM Journal on Control and Optimization, 1996, 34(4): 1441-1460. |
| [4] | Cardallaguet P, Quincampoix M, Saint-pierre P. Some algorithms for differential game with two-players and one target[J]. Mathematical Modeling and Numerical Analysis, 1994, 28(4): 441-461. |
| [5] | Cardallaguet P, Quincampoix M, Saint-pierre P. Pursuit differential games with state constraints[J]. SIAM Journal on Control and Optimization, 2002, 39(5): 1615-1632. |
| [6] | Gao Y, Lggeros J, Quincampoix M. On the reachability problem of uncertain hybrid systems[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1572-1586. |
| [7] | 张霞, 高岩, 夏尊铨. 追捕逃逸型微分对策问题的识别域判别[J]. 上海理工大学学报, 2012, 34(5): 452-455. Zhang X, Gao Y, Xia Z Q. Determining the discriminating domain of pursuit-evasion games[J]. Journal of University of Shanghai for Science and Technology, 2012, 34(5): 452-455. |
| [8] | Nikolai B, Varvara T. Numerical construction of viable sets for autonomous conflict control systems[J]. Mathematics, 2014(2): 68-82. |
| [9] | Aubin J P. Viability theory[M]. Boston, USA: Birkhauser, 1991. |
| [10] | Su R. On the linear equivalents of nonlinear system[J]. Systems and Control Letters, 1982, 2(1): 48-52. |
| [11] | Demyanov V F, Rubinov A M. Constructive nonsmoothanalysis[M]. Frankfurt am Main: Peterlang, 1995. |
| [12] | 高岩. 仿射非线性控制系统生存性的判别[J]. 控制理论与应用, 2009, 26(6): 654-656. Gao Y. Determining the viability for an affine nonlinear control system[J]. Control Theory and Applications, 2009, 26(6): 654-656. |
| [13] | Gao Y. Viability criteria for differential inclusions[J]. Journal of Systems Science and Complexity, 2011, 24(5): 825-834. |
| [14] | Clarke F H, Ledyaev Y S, Stern R J, et al. Nonsmoothanalysis and control theory[M]. Berlin, Germany: Springer-Verlag, 1998. |
| [15] | 高岩. 一类非线性控制系统可生存性的判别[J]. 信息与控制, 2005, 34(4): 510-512. Gao Y. Determining the viability for a class of nonlinear control systems[J]. Information and Control, 2005, 34(4): 510-512. |



