2. 中国科学院大学, 北京 100049;
3. 中国科学院网络化控制系统重点实验室, 辽宁 沈阳 110016
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Networked Control Systems, Chinese Academy of Sciences, Shenyang 110016, China
1 引言
水泥行业是典型的高耗能行业,水泥生产能源成本占到水泥生产总成本的50%~60%[1]. 目前,中国日产4 000吨以上水泥熟料生产线的平均综合能耗为119 kgce/t,与国际先进水平的107 kgce/t还有较大差距[2]. 为了提高生产过程能效,降低生产成本,我国2008年开始启动水泥企业能效对标工作,编写了《水泥企业能效对标指南》,形成了水泥企业能效对标指标体系并组织了相关企业开展能效对标活动[3]. 但是目前水泥能效对标存在两个主要问题: (1) 标杆数据陈旧. “BEST水泥”能效对标工具使用的能耗数据为2007年的数据,已不能适用当前水泥生产[4]. (2) 各水泥生产过程的能源消耗水平受到生产规模、原料质量、设备运行工况、生产环境等诸多因素的影响[5],采用均值法或者单独地和最佳生产实践相比往往会造成片面的对标结果[6].
为了建立科学的能耗标杆,国内外学者做了大量研究. 一种研究思路是将影响过程能耗的因素进行量化,然后分析各影响因素对过程能耗的影响,以建立适合具体过程的能效对标模型. 例如,Joshi等利用层次分析法建立了低温运输系统的对标体系框架,用于分析系统各因素对总能耗的影响[7];Yalicintas利用人工神经元网络方法建立了热带地区建筑能效对标模型,用于揭示各种能量输入对节能潜力的影响[8];Chung等利用回归模型建立了能源使用强度和其解释变量之间的能效对标模型,并将其应用于商业建筑的能效对标管理中[9];Wu等将设备能效函数在平衡点处进行泰勒级数展开,提出了设备能效评价模型[10];Kissock等建立了多变量转换点模型消除了环境和设备产量因素来评估设备或过程改造前后的能源节省量[11];王学雷采用非参数回归方法建立了原料与各种能源介质消耗指标之间的关系模型[12]. 以上研究工作可以有效地分析系统各因素对过程能耗的影响,但是水泥生产过程的能耗水平受到生料三率值、熟料产量、回转窑烧成带温度、磨机负荷、水泥粉磨细度、环境温度等各种生产因素影响. 这些影响因素往往不能使用变量进行量化且存在一定的耦合,若采用以上研究方式将不能建立合理的能效对标体系. 与其做大量的工作将影响因素剔除,不如将各种影响因素纳入企业能耗标杆中,建立包含各种影响因素的水泥生产企业实际能耗标杆. 基于这样一种研究思路,国内外学者也做了大量相关研究,例如,Szijjarto等建立了多层集成能源指标体系,综合所有生产因素对离散化工过程进行了能效和节能潜力的分析[13];Saygin等通过对全世界各能源密集型产业的能耗统计数据进行分析,按百分比确定各行业的能耗基准,实现对各行业能效提升潜力的分析[14];Laurijssen等通过对造纸行业能量流的分析,实现了该行业过程单元级的能效对标[15];Drumm等将工业过程用能分为固有能耗、静态损失能耗和动态损失能耗,建立了结构能效系统,可实现企业自身能效的纵向比较和行业内部的横向比较[16];耿志强等针对乙烯装置不同工艺、规模以及不同装置能耗数据分布特点,采用对数据分布适应性好的层次线性优化融合算法提取了生产过程的能耗指标[17];朱群雄等利用改进的K均值聚类方法将乙烯生产过程的各种能源数据进行融合,建立了包含各种影响因素的能耗虚拟标杆[18]. 以上研究工作可以综合生产过程多种能耗因素,使提取的能耗标杆具有客观性和可计算性,但在大时间尺度下,水泥生产过程的噪声数据和异常工况会降低能耗标杆的准确性和客观性. 因此,本文首先针对大时间尺度下,水泥生产过程各能耗变量历史数据的聚类数目因工况变化和各种噪声影响而无法直接获得的问题,提出改进的DBSCAN(density-based spatial clustering of applications with noise)算法对生产过程各能耗变量的历史数据分别进行聚类分析. 在得到各能耗变量历史数据的分类、聚类中心和方差后,以各聚类中心作为相应能耗变量的“虚拟传感器”,利用各聚类中心的方差,结合线性最小方差多传感器融合算法分别对各能耗变量的聚类中心进行融合获取水泥熟料生产过程中各能耗变量的数据标杆. 最后,通过对某水泥生产企业进行实例应用,得到该生产过程的实际能耗标杆,利用该标杆可客观揭示大时间尺度下水泥生产过程的运行状态和操作水平.
2 水泥企业能效对标体系目前,新型干法水泥生产工艺已经定型,其能量消耗具有一定的可比性. 水泥生产的主要能源介质包括煤、电、水、压缩空气、氮气、油. 由于水、压缩空气、氮气、油等在实际生产过程中所占的比例很小且难以测量,不纳入本文研究的能效对标指标体系中. 图 1所示为新型干法水泥生产的基本流程. 水泥生产过程能耗标杆建立的界区为: 从原料破碎开始到水泥成品输出为止,其主要包括原料破碎与均化、生料粉磨、煤粉制备、熟料烧成、水泥粉磨、水泥包装和输送等环节.
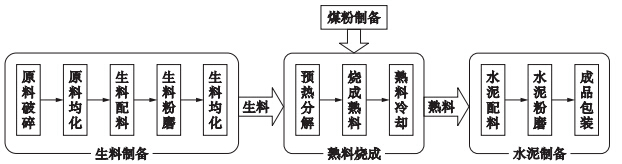 |
| 图 1 新型干法水泥生产的基本工艺流程图Fig. 1 The basic process flow of new dry cement manufacturing |
水泥行业GB/T 26281-2010《水泥回转窑热平衡、热效率、综合能耗计算方法》和GB/T 27977-2011《水泥生产电能能效测试及计算方法》给出了生产过程各环节边界的定义和各环节能耗的计算公式[19, 20]. 本文研究的水泥能耗指标主要包括: 生料制备电耗、煤粉制备电耗、熟料烧成电耗、熟料烧成煤耗、水泥粉磨电耗. 在大时间尺度下,水泥生产过程能耗水平可以采用式(1)所示的向量表示,其中Qszb、Qmzb、Qssc、Qsfm、Essm分别代表生料制备电耗(kW·h/t)、煤粉制备电耗(kW·h/t)、熟料烧成电耗(kW·h/t)、水泥粉磨电耗(kW·h/t)、熟料烧成煤耗(kgce/t).
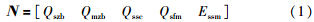
水泥生产过程的各环节既相互联系又相对独立,其运行工况主要受到原料质量、设备负荷率、过程参数、生产规模、环境条件等因素的影响. 而各生产环节的工况的变化导致其能耗指标的变化. 同时,由于各种因素的影响,生产过程的能耗数据往往包含有大量噪声,对生产能耗数据取算术平均或者取最优能耗指标通常难以准确地反映一个企业各生产环节实际能耗水平. 为了充分提取包含在历史数据中的有效信息来建立包含各种影响因素的能耗标杆,需要采用数据融合的方法来分析各生产环节的实际能耗水平.
3 改进的DBSCAN算法在水泥实际生产中,各过程单元能耗变量历史数据随着工况的变化其变量状态会发生一定的变化,有时还会出现异常状态,所以需要先对历史数据进行聚类分析,有效提取嵌入到历史数据中的相关信息. 为了避免历史数据中有效信息的丢失,需要分别对各过程单元能耗变量历史数据进行聚类,使聚类中心数目能够按各自工况进行调整,充分反映实际工况的变化. 各种聚类方法中,基于密度的聚类方法不需要预先知道聚类的数目,而且不会因为噪声数据而对聚类结果产生影响[21]. DBSCAN算法是利用区域数据密度的大小来区分数据类别的算法,它将密度相连的点聚为一类. 利用数据密度的连通性,该算法可以从包含噪声的数据空间中识别出任意形状的聚类. 该算法涉及到以下一些概念[22, 23, 24].
(1) 数据对象的邻域
数据空间中以数据对象o为中心,以ε为半径的区域称为数据对象o的ε领域.
(2) 核心对象
若数据对象o的ε邻域内含有的数据点达到某一个阈值,则称该点为核心对象.
(3) 直接密度可达
若p是数据空间的核心对象,且q在p的ε邻域内,则称p直接密度可达q.
(4) 密度可达
若存在核心对象序列p1,…pi,…pn,1≤i≤n,pi直接密度可达pi+1,则p1密度可达pn.
(5) 密度相连
若数据对象o密度可达数据对象p和q,则称p和q密度相连.
(6) 类
类是数据空间中的密度相连的数据集合.
(7) 噪声
不属于任何类的数据对象称为噪声.
数据空间中直接密度可达、密度可达、密度相连三者的关系如图 2所示. 由图 2可以看出,如果从任意的核心对象出发,不断向密度可达的数据空间扩展,最终可以得到一个密度相连的聚类簇. DBSCAN算法就是通过不断地搜索提取出以ε为邻域半径、MinPts为密度阈值的所有聚类. 该算法的具体流程如图 3所示.
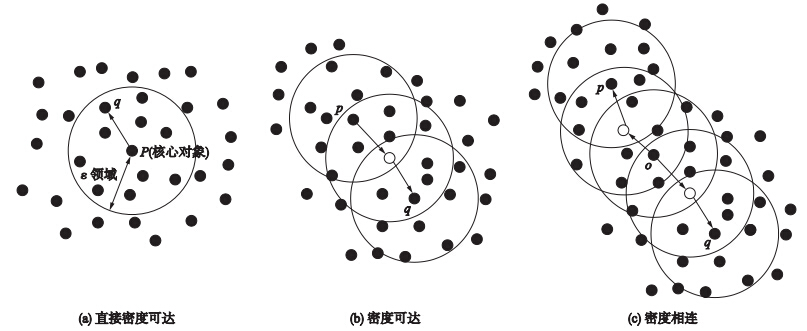 |
| 图 2 直接密度可达、密度可达和密度相连示意图Fig. 2 Schematic diagram of directly density-reachable,density-reachable and density-connected |
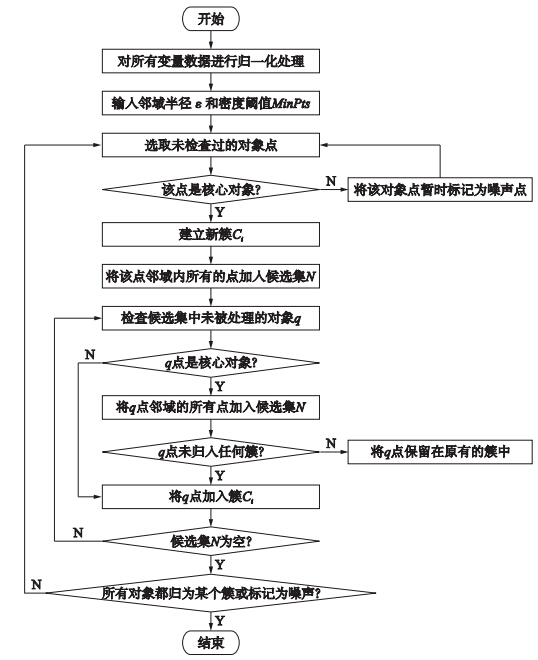 |
| 图 3 DBSCAN算法流程图Fig. 3 Flow chart of DBSCAN algorithm |
在实际应用中,我们对各能耗变量的数据分别进行聚类分析,由于水泥生产过程各能耗数据的量纲并不相同,为使所有数据的聚类采用相同的标准,即数据对象的邻域ε和密度阈值MinPts一致,在采用聚类算法之前需要对不同能耗变量的数据进行归一化处理. 由于测量噪声的影响,过程数据中往往存在超出变量正常取值范围的噪声数据,这里采用标准差标准化方法,如式(2)所示.

由图 3的算法流程可知,DBSCAN算法中获得密度可达的对象是通过对核心对象邻域内所有数据点的查询来实现的. 一般情况下,聚类的数据规模较大,若对核心对象邻域内的所有对象点依次进行查询,算法的执行效率会大大下降. 在对水泥生产过程能耗数据的聚类分析中,我们是将各能耗变量的数据单独进行聚类分析,聚类的数据空间变为一维. 在一维空间数据的聚类计算中,类的扩展方向只有两个,即比核心对象点数值大的方向(正向)和比核心对象点数值小的方向(负向). 一般情况下,数据对象点的邻域是相互覆盖的,大部分对象点可以不用当作密度可达扩展中的检测点. 这里,我们根据对象点到核心对象的距离来选择代表对象点进行密度可达扩展,减少区域查询的次数. 图 4是以一维数据空间中核心对象的正向邻域为例给出选择代表对象点进行密度可达扩展的具体算法流程.
由图 4的算法流程可知,改进的快速聚类算法通过由远到近选择性检查核心对象邻域范围内的对象点来扩展类. 当核心对象点处于密度区域内部时,该算法只需在其邻域内检查两次代表对象点(既正向和负向中距离核心对象点最远的点),这大大减少了区域对象点的查询次数,提高了算法的执行效率.
 |
| 图 4 改进的一维空间中密度可达搜索算法Fig. 4 Improved density-reachable search algorithm in one-dimensional space |
水泥生产过程各能耗变量数据标杆的提取实际上是对得到的聚类中心进行融合的问题. 该多变量融合问题是一个描述主题相同但聚类中心数目不同的多变量融合问题,因此需要采用最优状态估计对不同变量使用不同的加权权重. 所以,可将每一个能耗变量的聚类看作是多个传感器分别在聚类中心的测量值,每个聚类中心的方差即为每个传感器的测量方差. 基于线性最小方差的多传感器融合算法可以有效综合各聚类中心的相关信息,其融合结果的准确性会随着各聚类中心信息量的增加而提高[25, 26]. 采用该融合算法得到的估计值的方差小于多个聚类中心取均值所得到的估计值的方差[25].
假设某一个能耗变量X的n个聚类中心分别为X1,X2,…,Xn,它们是对变量X的无偏估计,其方差分别为σ12,σ22,…,σn2. 选用加权向量W=[W1 W2 … Wn]T对各聚类中心进行加权融合,则变量X的线性最小方差优化融合问题可以表示为


可以求得变量X的均方误差为
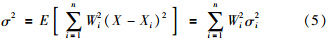
求取变量X的最小均方误差问题转换为在式(4)约束条件下求多元函数求极值问题. 可以求得σ2最小时所对应的加权因子为
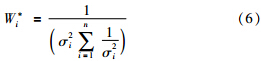
最小均方差为
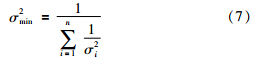
利用各能耗变量的聚类中心以及各密度类所包含的全部数据,可以计算得到各变量关于每一个聚类中心的方差. 其计算公式如式(8)所示.
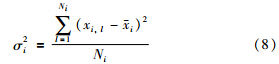
为了检验线性最小方差融合算法所得到的结果是否合理,我们定义一个置信度函数B来衡量样本数据对于融合结果的置信程度.
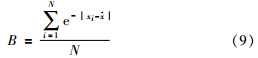
本文选用某水泥生产企业2012年12个月的能耗相关数据作为验证本文提出的融合方法的输入数据. 为了减少噪声因素和其它不可测因素的影响,选用能耗变量的统计时间尺度为每班次(8 h). 选用该时间尺度可以有效地滤除生料成分、预热器进料速率、分解炉出口温度、篦冷机篦下压力、选粉机转速等波动相对频繁的因素的干扰,有利于找出影响生产过程整体能耗的真正因素. 对选用的1 098组数据按式(2)进行归一化处理,并采用本文提出的改进的DBSCAN快速聚类方法进行聚类分析. 各能耗变量选取统一的密度阈值MinPts=9,即3天内能耗数据的波动范围在某一个邻域范围内,则认定这些数据可聚为一簇. 聚类算法的邻域范围由经验式(10)确定.
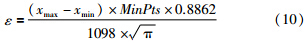
| 类数 | Qszb(kW·h/t) | Qmzb(kW·h/t) | Qssc(kW·h/t) | Qsfm(kW·h/t) | Essm(kgce/t) | |||||
| 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 14.949 3 | 0.083 5 | 20.082 1 | 0.002 6 | 19.506 5 | 0.002 7 | 28.179 0 | 0.000 1 | 90.041 4 | 0.027 7 |
| 3 | 15.688 6 | 0.015 9 | 21.153 5 | 0.244 0 | 20.798 3 | 0.273 0 | 28.812 4 | 0.018 8 | 92.040 1 | 0.239 3 |
| 4 | 16.412 0 | 0.089 0 | 22.279 0 | 0.006 9 | 21.978 1 | 0.001 5 | 29.210 5 | 0.003 0 | 93.969 3 | 0.204 2 |
| 5 | 17.705 4 | 0.208 6 | — | — | — | — | 30.131 3 | 0.199 0 | 95.052 7 | 0.017 0 |
| 6 | — | — | — | — | — | — | 31.306 2 | 0.034 6 | — | — |
| 7 | — | — | — | — | — | — | 32.374 6 | 0.001 1 | — | — |
由表 1可以看出,由于运行工况等因素的影响,基于密度的聚类方法将各能耗变量的数据聚为了不同数目的类. 由于数据统计期间存在停产整修,各能耗变量均存在一个均值为0、方差为0的类,因此在数据融合计算中忽略该类提供的信息. 煤粉制备和熟料烧成环节因为工况相对稳定,单位产品电耗数据的聚类数目仅为3类,而水泥粉磨环节的电耗数据的聚类数目为6类,表明其运行在多个不同的工况下. 表 2为同一能耗历史数据基于传统DBSCAN算法的聚类结果. 与表 1的结果进行对比可以看出,两种方法得到的各变量聚类数目一致,各聚类均值和方差存在较小误差,原因是计算顺序的不同,导致处于聚类中心边缘的点被归入了不同的类.
| 类数 | Qszb(kW·h/t) | Qmzb(kW·h/t) | Qssc(kW·h/t) | Qsfm(kW·h/t) | Essm(kgce/t) | |||||
| 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 14.585 1 | 0.082 1 | 20.109 1 | 0.002 5 | 19.504 0 | 0.002 6 | 28.210 9 | 0.000 1 | 90.115 3 | 0.023 4 |
| 3 | 15.621 1 | 0.255 9 | 21.159 5 | 0.244 0 | 20.786 2 | 0.282 6 | 28.798 1 | 0.015 8 | 92.216 2 | 0.231 9 |
| 4 | 16.517 7 | 0.000 9 | 22.279 0 | 0.006 9 | 21.947 3 | 0.001 2 | 29.194 2 | 0.003 5 | 93.810 9 | 0.237 4 |
| 5 | 17.424 2 | 0.208 6 | — | — | — | — | 30.218 5 | 0.179 9 | 95.428 4 | 0.015 6 |
| 6 | — | — | — | — | — | — | 31.453 3 | 0.031 4 | — | — |
| 7 | — | — | — | — | — | — | 32.393 1 | 0.001 4 | — | — |
表 3列出了改进的DBSCAN算法和传统的DBSCAN算法在处理1 098组数据时的聚类有效性指标和算法执行时间.
| 指标 | 改进的DBSCAN | 传统的DBSCAN | ||||||||
| Qszb | Qmzb | Qssc | Qsfm | Essm | Qszb | Qmzb | Qssc | Qsfm | Essm | |
| 聚类密集性 | 0.044 0 | 0.024 3 | 0.025 8 | 0.016 5 | 0.002 4 | 0.048 3 | 0.025 8 | 0.025 7 | 0.014 2 | 0.008 9 |
| 聚类邻近性 | 0.379 2 | 0.438 2 | 0.409 3 | 0.368 6 | 0.431 4 | 0.399 5 | 0.434 5 | 0.406 5 | 0.313 6 | 0.285 2 |
| 聚类质量 | 0.788 4 | 0.768 7 | 0.782 5 | 0.807 5 | 0.783 1 | 0.776 1 | 0.769 9 | 0.783 9 | 0.836 1 | 0.852 9 |
| 算法执行时间/s | 0.267 8 | 0.136 7 | 0.140 9 | 0.374 8 | 0.284 6 | 2.309 1 | 2.163 2 | 2.098 2 | 2.547 9 | 2.394 7 |
由表 3的对比可以看出,对于各能耗变量的聚类结果,基于改进的DBSCAN算法的聚类密集性(指标范围在[0, 1]之间,越小越好)、聚类邻近性(指标范围在[0, 1]之间,越小越好)和聚类质量(指标范围在[0, 1]之间,越大越好)要好与传统的DBSCAN算法. 其原因是改进的DBSCAN算法将处于聚类中心边缘的点归为了确定的簇,而在传统的DBSCAN算法中,处于聚类中心边缘的点会因为聚类过程计算顺序的不同而归入不同的簇. 与传统的DBSCAN算法相比,改进的DBSCAN算法的执行时间短. 对于更大数据规模的聚类或在线滚动动态能效对标中,改进的DBSCAN算法相对于传统的DBSCAN算法将明显提高算法的执行效率. 对于同等数据规模的聚类运算,改进的DBSCAN算法的聚类时间依赖于数据的密度分布. 数据的密度分布相对集中(即聚类数目少),算法的执行时间短;数据的密度分布相对分散(即聚类数目多),算法的执行时间长.
根据表 1所列各能耗变量的方差及式(6),可以计算得到各能耗变量聚类中心的加权向量,如式(11)~式(15)所示. 同时,利用各能耗变量的所有聚类中心和式(3)得到各能耗变量的综合实际标杆,如式(16)所示. 该企业各能耗变量的平均值如式(17)所示.
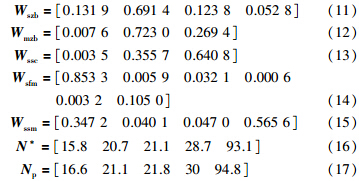
表 4列出了采用均值法和数据融合方法得到的各能耗变量标杆值的置信度. 由表 4可以看出,对于计算结果的置信度这一指标,本文提出的数据融合方法要好于均值法,其原因是,基于密度的聚类方法将各能耗变量中的异常值进行了剔除,而均值法采用的是所有的测量数据. 另外,线性最小方差融合算法充分利用了各数据簇的方差信息,使离散度越小的数据簇在能耗标杆的融合中所占的权值越大,而均值法将所有数据按照相同的权值进行处理.
| 方法 | Qszb | Qmzb | Qssc | Qsfm | Essm |
| 均值法 | 0.425 4 | 0.604 3 | 0.438 1 | 0.456 9 | 0.415 6 |
| 数据融合法 | 0.428 9 | 0.653 5 | 0.591 6 | 0.507 3 | 0.461 8 |
图 5所示为国内水泥企业能耗最佳实践标杆、实例企业平均能耗和实例企业实际能耗标杆的对比曲线图. 图中竖线上下两端中括号内的数据为各能耗变量的取值范围.
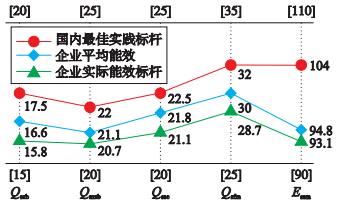 |
| 图 5 水泥企业能耗标杆曲线Fig. 5 Energy consumption benchmark curves of the cement enterprise |
由图 5中能耗标杆曲线可知,该水泥企业实际能耗远低于国内最佳实践标杆. 其主要原因有以下4点: (1) 国内水泥企业能耗最佳实践标杆的数据为2007年的数据,数据较为陈旧. 而近几年国内水泥企业装备和技术水平发展迅速,重大技术改造可大幅度提高企业能效水平;(2) 该实例企业处于优质矿区,开采容易,使得原料制备环节能耗较低;(3) 该实例企业原料品位高,生料易烧性好,使得水泥熟料的煤耗远远低于最佳实践标杆水平;(4) 由于原料品味较高,该企业各环节年平均负荷率在110%以上,远高于设计生产能力,降低了单位产品的固有能耗. 另外,由数据融合得到的水泥企业实际能耗标杆中各能耗变量的值要小于该企业能耗变量的平均值,揭示了该企业能效提升的空间,表明该实际能耗标杆对企业节能降耗起到一定的指导价值.
6 结论本文针对大时间尺度下水泥生产过程能耗变量的聚类数目因工况变化和噪声污染而无法直接获得特点,提出了改进的DBSCAN算法,并结合线性最小方差融合算法来建立水泥企业实际能耗标杆. 水泥企业的应用实例表明,本文提出的改进的DBSCAN算法可以有效地提高聚类质量、降低算法的执行时间,适用于数据量较大的聚类. 通过数据融合得到的企业实际能耗标杆能够包含生产过程综合影响因素,合理反映企业实际能耗水平,揭示企业节能潜力. 此外,本文采用的方法是基于数据驱动的,可为其它工业过程能耗标杆的建立提供参考.
| [1] | Wang J F, Dai Y P, Gao L. Exergy analyses and parametric optimizations for different cogeneration power plants in cement industry[J]. Applied Energy, 2009, 86(6): 941-948. |
| [2] | 曾学敏, 余为民, 胡芝娟, 等. 水泥企业能效对标指南综述[J]. 水泥, 2009, 36(6): 1-9. Zeng X M, Yu W M, Hu Z J, et al. A review of cement enterprise energy efficiency benchmarking guide[J]. Cement, 2009, 36(6): 1-9. |
| [3] | 赵家荣. 重点耗能行业能效对标指南[M]. 北京: 中国环境科学出版社, 2009. Zhao J R. An energy efficiency benchmarking guide for key energy-consuming industries[M]. Beijing: China Environmental Science Press, 2009. |
| [4] | 熊华文. 水泥企业能效对标分析工具介绍[J]. 中国水泥, 2008, 23(12): 64-66. Xiong H W. Introductions of energy efficiency benchmarking analysis tools for cement enterprises[J]. China Cement, 2008, 23(12): 64-66. |
| [5] | Madlool N A, Saidur R, Rahim N A, et al. An overview of energy savings measures for cement industries[J]. Renewable and Sustainable Energy Reviews, 2013, 19(1): 18-29. |
| [6] | Baileya J A, Gordona R, Burtonb D, et al. Energy conservation on Nova Scotia farms: Baseline energy data[J]. Energy, 2008, 33(7): 1144-1154. |
| [7] | Joshi R, Banwet D K, Shankar R. A Delphi-AHP-TOPSIS based benchmarking framework for performance improvement of a cold chain[J]. Expert Systems with Applications, 2011, 38(8): 10170-10182. |
| [8] | Yalcintes M. An energy benchmarking model based on artificial neural network method with a case example for tropical climates[J]. International Journal of Energy Research, 2006, 30(14): 1158-1174. |
| [9] | Chung W, Hui Y V, Lam Y M. Benchmarking the energy efficiency of commercial buildings[J]. Applied Energy, 2006, 83(1): 1-14. |
| [10] | Wu L M, Chen B S. Modeling of energy efficiency indicator for semiconductor industry[C]//2007 IEEE International Conference on Engineering and Engineering Management. Piscataway, NJ, USA: IEEE, 2007: 822-826. |
| [11] | Kissock J K, Eger C. Measuring industrial energy savings[J]. Applied Energy, 2008, 85(5): 347-361. |
| [12] | 王学雷. 面向乙烯生产流程的能源消耗动态定标方法[J]. 计算机与应用化学, 2010, 27(9): 1166-1170. Wang X L. A dynamic benchmarking method for energy consumption of ethylene production process[J]. Computers and Applied Chemistry, 2010, 27(9): 1166-1170. |
| [13] | Szijjarto A, Papadokonstantakis S, Hungerbuhler K. Model-based identification and analysis of the energy saving potential in batch chemical processes[J]. Industrial & Engineering Chemistry Research, 2012, 51(34): 11170-11182. |
| [14] | Saygin D, Worrell E, Patel M K, et al. Benchmarking the energy use of energy-intensive industries in industrialized and in developing countries[J]. Energy, 2011, 36(11): 6661-6673. |
| [15] | Laurijssen J, Faaij A, Worrell E. Benchmarking energy use in the paper industry: A benchmarking study on process unit level[J]. Energy Efficiency, 2013, 6(1): 49-63. |
| [16] | Drumm C, Busch J, Dietrich W, et al. STRUCTese(R)-Energy efficiency management for the process industry[J]. Chemical Engineering and Processing: Process Intensification, 2013, 67(S1): 99-110. |
| [17] | 耿志强, 石晓赟, 顾祥柏, 等. 层次线性优化融合及在乙烯行业能耗指标提取中的应用[J]. 化工学报, 2010, 61(8): 2056-2060. Geng Z Q, Shi X Y, Gu X B, et al. Hierarchical linear optimal fusion algorithm and its application in ethylene energy consumption indices acquisition[J]. CIESC Journal, 2010, 61(8): 2056-2060. |
| [18] | 朱群雄, 石晓赟, 顾祥柏, 等. 基于时序数据融合的乙烯装置能效价值研究及应用[J]. 化工学报, 2010, 61(10): 2620-2626. Zhu Q X, Shi X Y, Gu X B, et al. Time-series data fusion and its application to energy efficiency value for ethylene plants[J]. CIESC Journal, 2010, 61(10): 2620-2626. |
| [19] | GB/T 26281-2010. 水泥回转窑热平衡、热效率、综合能耗计算方法[S]. GB/T 26281-2010. Calculation methods for heat balance, heat efficiency and comprehensive energy consumption of cement rotary kiln[S]. |
| [20] | GB/T 27977-2011. 水泥生产电能能效测试及计算方法[S]. GB/T 27977-2011. Test and calculation methods of electricity efficiency of cement production[S]. |
| [21] | 向培素. 聚类算法综述[J]. 西南民族大学学报: 自然科学版, 2011, 37(5): 112-114. Xiang P S. Survey of clustering algorithm[J]. Journal of Southwest University for Nationalities: Natural Science Edition, 2011, 37(5): 112-114. |
| [22] | 孙凌燕, 杨明, 任建斌. 一种基于相对密度的快速聚类算法[J]. 微电子学与计算机, 2009, 26(12): 109-111. Sun L Y, Yang M, Ren J B. A fast relative density-based clustering algorithm[J]. Microelectronics & Computer, 2009, 26(12): 109-111. |
| [23] | Tripathy A, Maji S K, Patra P K. FDCA: A fast density based clustering algorithm for spatial database system[C]//2011 2nd International Conference on Computer & Communication Technology. Piscataway, NJ, USA: IEEE, 2011: 21-26. |
| [24] | Tsai C F, Sung C Y. DBSCALE: An efficient density-based clustering algorithm for data mining in large databases[C]//2010 2nd Pacific-Asia Conference on Circuits, Communications and System: Vol.1. Piscataway, NJ, USA: IEEE, 2010: 98-101. |
| [25] | 汪平平, 张歆, 刘深. 基于线性最小方差和递归最小二乘的融合算法[J]. 探测与控制学报, 2013, 35(4): 33-36. Wang P P, Zhang X, Liu S. Fusion algorithm based on linear minimum variance and recursive least squares[J]. Journal of Detection & Control, 2013, 35(4): 33-36. |
| [26] | Fong L W. Multi-sensor data fusion via federated adaptive filter[C]//2010 International Symposium on Computer, Communication, Control and Automation: Vol.1. Piscataway, NJ, USA: IEEE, 2010: 209-212. |
| [27] | 程建兴, 史仪凯. 基于多传感器数据融合的鲁棒自适应滤波算法[J]. 自动化仪表, 2008, 29(6): 65-67. Cheng J X, Shi Y K. A robust self-adaptive filtering based on multi-sensor data fusion[J]. Process Automation Instrumentation, 2008, 29(6): 65-67. |



